END随机变量序列加权和的几乎处处收敛性

邓 新， 夏凤熙， 王学军

（安徽大学 数学科学学院，安徽 合肥 230601）

END随机变量序列加权和的几乎处处收敛性

邓 新， 夏凤熙， 王学军

（安徽大学 数学科学学院，安徽 合肥 230601）

文章主要讨论了同分布条件下END随机变量序列加权和在相关的矩条件和权系数条件下的几乎处处收敛性，并得到了在随机控制条件下的相应结果，该结果推广了独立随机变量序列和负相依随机变量序列几乎处处收敛性质的相应结果。

END随机变量；加权和；几乎处处收敛性；随机控制

许多统计问题的研究中，一般假设随机变量是独立的，但在实际问题中，这样的假设是不合理的，所以把独立的概念进行推广是许多统计学家的研究方向，其中END（extended negatively dependence）随机变量就是一类非常普遍且非独立的随机变量。

定义1 称随机变量序列｛Xn，n≥1｝是END（extended negatively dependence，简称END）的，若存在常数M＞0，使得（1）式、（2）式对任意的n≥1和所有的实数x1，x2，…，xn成立，即

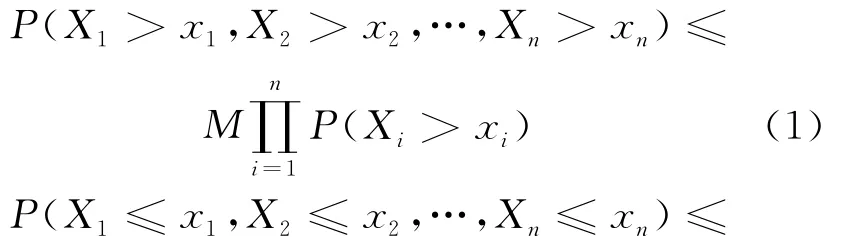
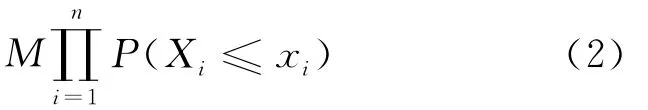
随机变量的概念是由文献［1］引入的。若M＝1，则END变量即为负象限相依（ND）变量，有关ND序列的概念，可参考文献［2］。文献［2］指出负相依（NA）随机变量也是ND的，从而NA随机变量也是END的。文献［1］指出END变量不仅包含一些常见的负相依变量，还包含一些正相依变量。因此，END序列是一类非常广泛的相依变量，研究其极限性质具有重要的理论意义和实际意义。

关于END随机序列的概率不等式、矩不等式、概率极限性质以及END随机序列的一些应用，主要有以下成果：文献［1］得到了关于重尾相关随机变量的精细大偏差；文献［3］研究了基于重尾相关随机变量中偏差的充分和必要条件；文献［4］建立了END随机变量的强大数定理，并且给出其在风险理论和更新理论中的应用；文献［5］得到了一致变化尾下END序列随机加权和的精确大偏差；文献［6］建立了END序列的一些概率不等式和矩不等式，并且给出其在逆矩中的应用；文献［7］研究了END序列的基本更新定理；文献［8］研究了END序列加权和以及END阵列加权和的完全收敛性。因为END序列比独立序列、NA序列以及ND序列更弱，所以研究END随机变量的概率极限性质以及统计大样本理论更有意义。本文的目的在于研究同分布END随机序列加权和的几乎处处收敛性，该结果推广了独立序列和ND随机序列的相应结果；同时还研究不同分布场合下END随机序列加权和的几乎处处收敛性，但要用到随机控制的条件，其定义如下：

定义2 称随机变量序列｛Xn，n≥1｝被随机变量X随机控制，是指如果存在正常数C，使得对任意的n≥1和x≥0，有

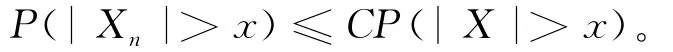
引理1 若随机变量X1，X2，…，Xn是END的，则下列命题成立［3］：

（1）若f1，f2，…，fn是非降（或非增）函数，则随机变量f1（X1），f2（X2），…，fn（Xn）是END的。

（2）对任意的n≥1，存在常数M＞0，使得（3）式成立，即

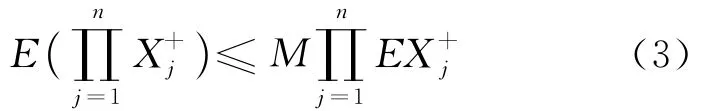
其中，＝max｛0，Xj｝。

引理2 若｛Xn，n≥1｝是END随机变量序列，｛tn，n≥1｝为非负（或非正）的常数序列，则对任意n≥1，存在常数M＞0，使得（4）式成立［6］，即

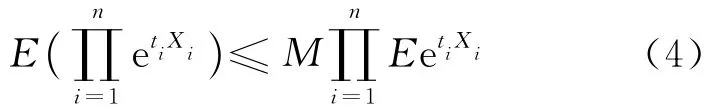
本文的主要结果及其证明如下。

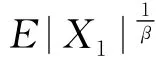
其中，c为常数且0＜c＜∞。记p＝min（1／β，2），存在常数α＞0，使得对所有的n≥1，有

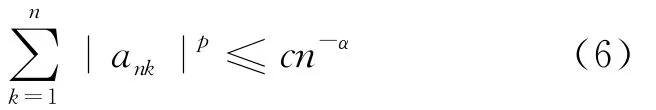
则有：

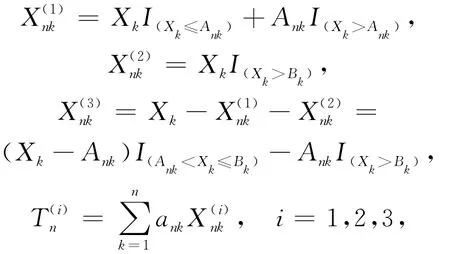
则有：

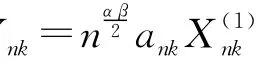
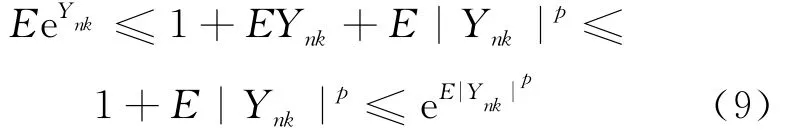
由引理2、（5）式、（8）式、（9）式及｜｜≤Xk，p≤1／β，E｜X1｜p＜∞，得

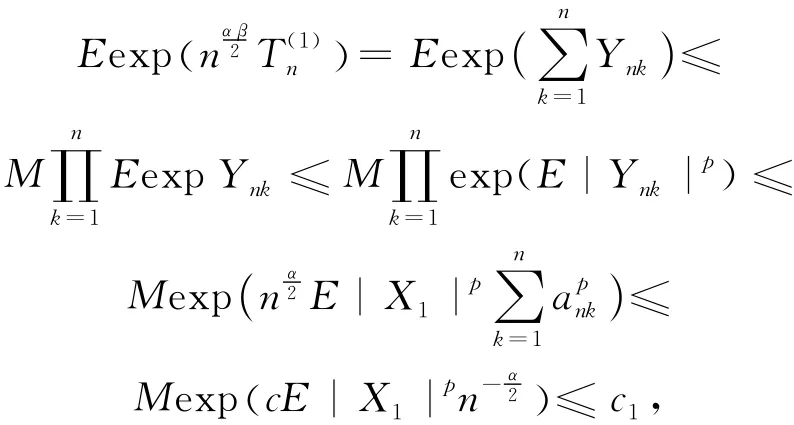
其中，c1为正常数。由Markov不等式及级数收敛性得：

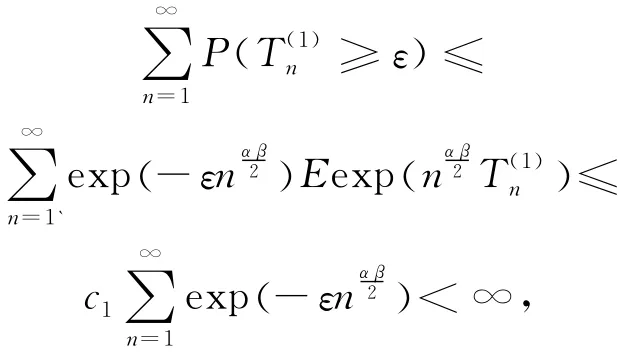
由 Borel－Cantelli引理，P≥ε，i.o.）＝0，所以有：

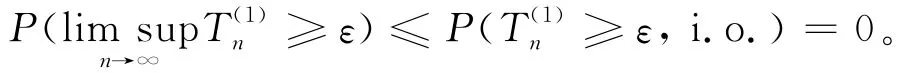
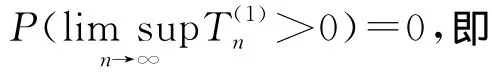
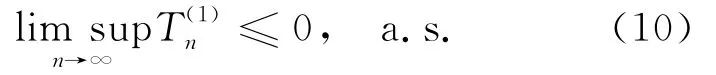
由｛Xn，n≥1｝同分布以及（3）式，有

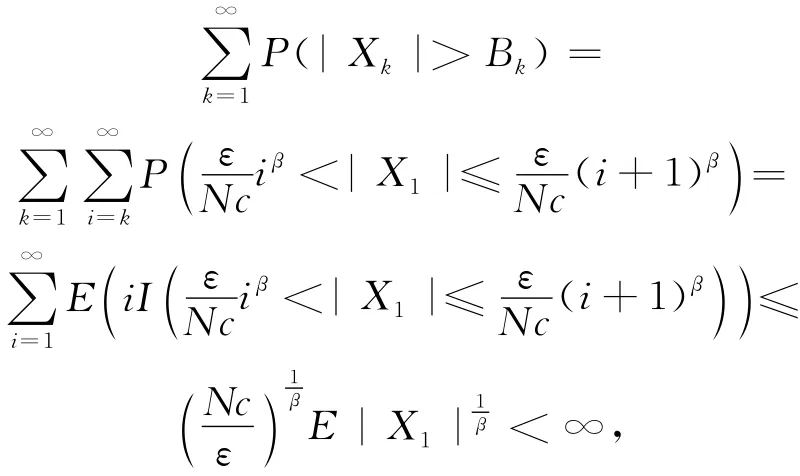
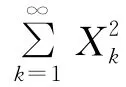
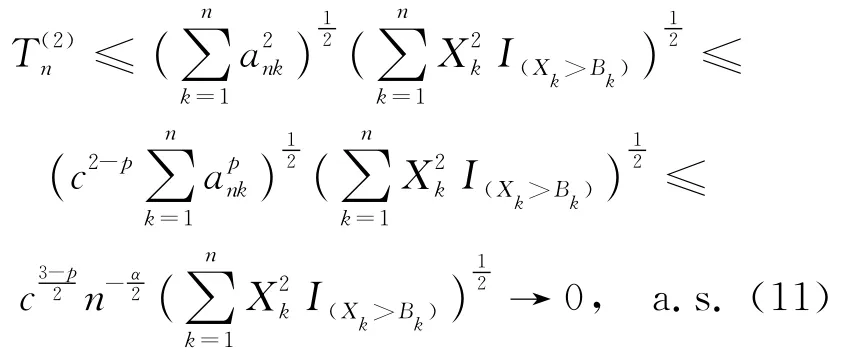
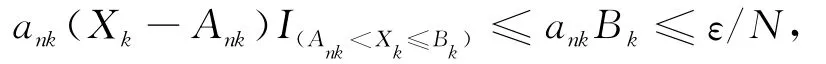
所以有：

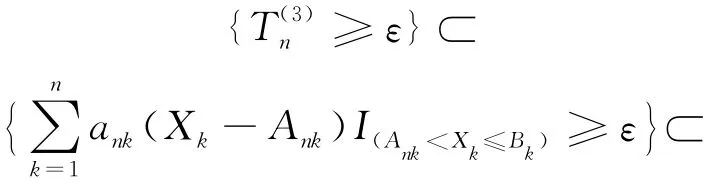
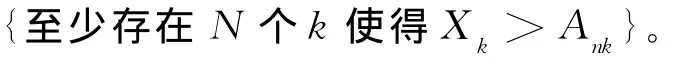
注意到｛Xn，n≥1｝为同分布的END随机变量序列且pβ≤1，故由（6）式可得：

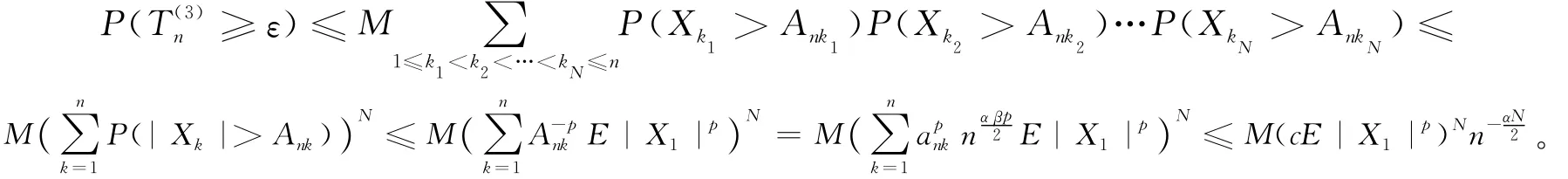
由于αN／2＞1，所以对任意ε＞0，有

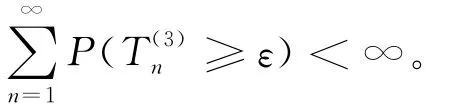
类似于（10）式的证明，可以得到：

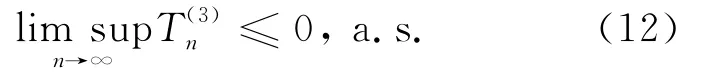
结合（8）式、（10）～（12）式，得到：

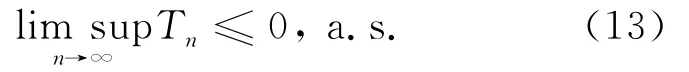
在（13）式中用－Xi代替Xi，得到

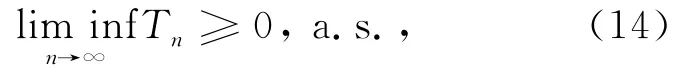
从而有（7）式成立。

本文的主要结论对被随机控制的END随机变量也是成立的，证明过程与定理1的证明类似，但要用到文献［9］中的引理4.1.6。

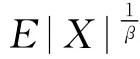
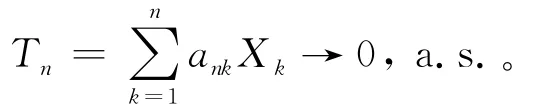
［1］Liu Li.Precise large deviations for dependent random variables with heavy tails［J］.Statistical Probability Letters，2009，79：1290－1298.

［2］Joag－Dev K，Proschan F.Negative association of random variable with application［J］.Annals of Statistics，1983，11（1）：286－295.

［3］Liu Li.Necessary and sufficient conditions for moderate deviations of dependent random variables with heavy tails［J］.Science China Series A： Mathematics，2010，53（6）：1421－1434.

［4］Chen Y，Chen A，Ng K W.The strong law of large numbers for extended negatively dependent random variables［J］.Journal of Applied Probability，2010，47：908－922.

［5］Chen Y，Yuen K C，Ng K W.Precise large deviations of random sums in presence of negative dependence and consistent variation［J］.Methodology and Computing in Applied Probability，2011，13 （4）：821－833.

［6］Shen A T.Probability inequalities for END sequence and their applications［J］.Journal of Inequalities and Applications，2011，2011（1）：1－12.

［7］Wang Y B，Cheng D Y.Basic renewal theorems for a random walk with widely dependent increments and their applications［J］.Journal of Mathematical Analysis and Applications，2011，384：597－606.

［8］Wang X J，Hu T C，Volodin A，et al.Complete convergence for weighted sums and arrays of rowwise extended negatively dependent random variables［J］.Communications in Statistics：Theory and Methods，2013，42：2391－2401.

［9］吴群英.混合序列的概率极限理论［M］.北京：科学出版社，2006：173－175.

Almost sure convergence of weighted sums of END random variable sequences

DENG Xin， XIA Feng－xi， WANG Xue－jun
（School of Mathematical Sciences，Anhui University，Hefei 230601，China）

This paper deals with the almost sure convergence of weighted sums of identically distributed extended negatively dependent（END）random variables under the conditions of moments and weight coefficients.The corresponding result under the condition of stochastic domination is also obtained.The result obtained in the paper extends the corresponding one of independent random variable sequence and negatively dependent random variable sequence.

extended negatively dependent（END）random variable；weighted sum；almost sure convergence；stochastic domination

O211.4

A

1003－5060（2014）06－0761－03

10.3969／j.issn.1003－5060.2014.06.024

2013－06－01；

2013－09－02

安徽省自然科学基金青年资助项目（1208085QA03；1308085QA03）；安徽大学大学生科研训练资助项目（KYXL2012007）

邓 新（1989－），女，山东滕州人，安徽大学硕士生；

王学军（1981－），男，安徽合肥人，博士，安徽大学副教授，硕士生导师.

（责任编辑 张淑艳）