闭复区间矩阵的逆

陈福川

（琼台师范高等专科学校，海南海口 571158）

一 预备知识

定义1．1［1］如果m×n个元素均为闭复区间数Z ij∈I（C）i=1，2，……mj=1，2，……n，则由m×n个元素构成的m×n阶矩阵

记为E（C），表示C上的所有闭复区间矩阵．

特别的当m=n时，则称为n阶闭复区间矩阵，记为En（C）

定义 1．2［1］形如

的矩阵称为单位矩阵．这里的1+i=［1－，1+］+［1－，1+］i=［1 1］+［1 1］i

形如

的矩阵称为零矩阵．这里的0=［0－，0+］+［0－，0+］i=［0 0］+［0 0］i

二 闭复区间矩阵的伴随矩阵及逆矩阵

定义2．1 设

是一个闭复区间矩阵，Zij的代数余子式是Eij，矩阵

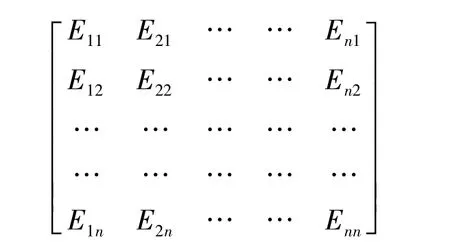
称为E的伴随矩阵，记为E*．

定义2．2 设E是一个n阶闭复区间矩阵，如果存在矩阵B∈E（C），使得

则称E是可逆的，记为E－1．

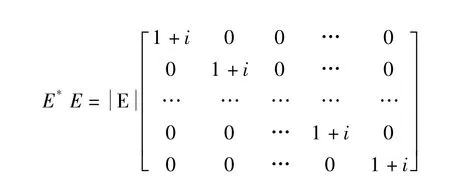
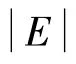
证明：设E，E－1互逆，那么就有

证毕

例：

三 小结

本文在文献［1］基础上，给出闭复区间矩阵伴随矩阵和逆矩阵，为闭复区间矩阵应用到实际中奠定了扎实基础。

［1］赵志青，石春．闭复区间矩阵及其应用初步［J］．电脑知识与技术，2014（6）．

［2］马生全．模糊复分析理论基础［M］．北京：科学出版社，2010．

［3］樊恽，钱吉林，岑嘉评，刘恒，穆汉林．代数学大词典［M］．武汉：华中师范大学出版社，1994．

［4］钟玉泉．复变函数论［M］．北京：高等教育出版社（第三版），2014．