不确定需求条件下小型制造企业有限产能分配决策研究*

韩正涛，张毕西

(广东工业大学 管理学院，广州 510520)

不确定需求条件下小型制造企业有限产能分配决策研究*

韩正涛，张毕西

(广东工业大学 管理学院，广州 510520)

文章主要研究了在考虑产能有限的条件下小型制造企业的产能分配决策问题。当一个小型制造企业在面临不确定需求的条件下，如何合理地分配恰当比例的产能给相应的产品，以防止因某种产品的短缺或过剩而带来的不必要的收益损失。文中给出了小型制造企业同时生产两种需求服从均匀分布的产品实现利润最大化时的产能分配最优模型。并通过模型解的存在性和求解的过程以及算例验证了模型的可靠性。

不确定需求；小型制造企业；均匀分布；产能分配

0 引言

随着当今世界经济的迅猛发展，小型制造企业也不再仅局限于生产一种型号的产品，更多的小型制造企业开始涉足两种甚至以上品种的产品生产，而各种产品给企业带来的收益又不尽相同，在复杂多变的、不确定的需求环境下，企业如何对有限的产能进行合理的分配以实现利润最大化的问题，成了众多企业家和学者关注的热点。Reyes[1]研究了若制造商能够充分利用好市场信息，可以有效地降低库存水平；Ji and Shao[2]提出了一个智能优化算法解决了模糊需求条件下具有资金约束的报童问题；陈炜婷等[3]给出了订单驱动生产系统产能分配与订单接受的优化决策模型；范志宁[4]从收益管理的角度研究了产能分配的问题；刘浪等[5]研究了模糊预测型线性规划在矿山产能分配中的应用；Tang 等[6]发展了不确定需求条件下的供应链中风险供应商定价和订货策略。但之前的一些研究对象往往针对于中大型制造企业或供应链环境下而言，研究侧重点主要集中在定价策略、库存、订单接受、产品数量等方面，产品种类繁多，对于品种少、需求不确定的小型制造企业适用性不强。基于此，本文从小型制造企业同时生产两种产品的角度出发，探究不确定需求条件下的小型制造企业有限产能分配决策问题。

1 问题描述

在某小型制造企业中共用一条流水线生产两种互相不可替代的产品，两种产品的需求量具有无法预知的复杂多变性与不确定性，且该企业短期内的产能是有限的，即不可能进行产能扩张。假设两种产品的需求为相互独立的均匀分布，并且两种产品给企业带来的收益也不相同，这时企业所要面对的决策问题是，单阶段内在两种产品的需求不确定的情况下，如何对两种产品共用的有限产能进行合理的分配，以取得最大的收益。

对本文中的符号作如下说明：

(1)f1(x)，f2(x)分别为产品一和产品二在需求均服从均匀分布且相互独立情况下的概率密度函数；

(2)p1，p2分别为产品一和产品二的售价；c1，c2分别为产品一和产品二的生产成本；

(3)D1，D2分别为产品一和产品二的实际市场需求量；

(4)S为总产能，θ1为分配给产品一的产能比例，θ2为分配给产品二的产能比例；

(5)R为总收益期望值。

在文献[4]的基础上可以得到下面的模型：

MaxR=

(p1-c1)·min{D1,θ1S}+(p2-c2)·min{D2,θ2S}

(1)

即

(2)

由于产能是有限的，因此两种产品分配的产能比例之和不能大于1，故有约束θ1+θ2≤1 ，即分配给两种产品产能之和不能超过总产能S；同时由于分配给两种产品的产能非负，还必须满足约束条件θ1≥0,θ2≥0；另外两种产品的售价均高于生产成本，即p1>c1,p2>c2。综合上述约束条件，可以得到下面的模型：

(3)

2 模型求解

将R对θ1和θ2分别求偏导数可得：

在ESP教学在国内高校逐步开展的同时，ESP教学中一些概念亟待厘清，一些问题需要解决。秦秀白(2003)曾指出我国高校ESP教学问题存在三个方面问题：1）未解决好专门用途英语在高校英语教育中的定位问题；2）对专门用途英语的性质和教学原则理解不一；3）对专门用途英语的教学方法研究不够深入。梁雪松(2006)和谷志忠(2010)调查和讨论我国高校中ESP教学的困境。刘梅(2013)从教学师资和教学课时两方面指出ESP差强人意的教学效果。杨枫(2013)直接指出目前国内ESP教学鲜有成功案例。归纳众学者的观点和基于自身教学实践，笔者认为目前高校ESP教学突出问题主要体现在以下三个方面：

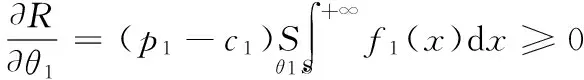
(4)

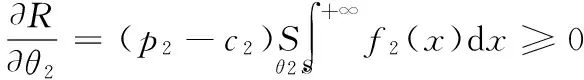
(5)

由(4)、(5)式可知，R随着θ1和θ2的增大而单调递增，当θ1+θ2=1时，R取得最大值。

将θ2=1-θ1代入(3)式得:

(6)

设与f1(x)，f2(x)相对应的需求分布函数分别为F1(x)，F2(x)，则对(6)式整理可得：

(7)

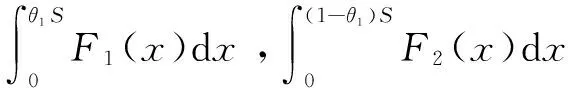
将(7)式中的R对θ1依次求一阶导数和二阶导数得：

(8)

(9)

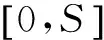
(10)

(11)

服从均匀分布的分布函数为

(12)

联立(11)、(12)式可得：

(13)

(14)

令

(15)

则

(16)

满足(16)式中的θ1，即是求得的企业在取得最大收益情况下分配给产品一的产能比例值。

3 算例

某小型手机充电器制造企业只生产两种型号的需求量不确定的手机充电器A和B，该企业的最大生产能力为200的单位，已知A型号的生产成本是20元，售价是50元；B型号的生产成本是40元，售价是80元。A、B两种充电器的市场需求分别服从[90,200]和[30,140]上的均匀分布，求按何种比例分配产能给A、B两种型号的充电器，才能使企业收益最大化。

即应当分配给A型号充电器的产能比例占总产能的60%，即120个单位；相应地分配给B型号充电器的产能比例占总产能的40%，即80个单位。

此时企业取得的收益最大化，为：

+(80-40)×[(1-60%)×200

=7489(元)

4 结论

在复杂多变、需求不确定的环境下，如何在产能有限的条件下合理地分配产能以实现收益最大化是众多小型制造企业面临的棘手问题。本文研究了单阶段决策情况下，需求服从均匀分布的小型制造企业同时生产两种产品时的有限产能的分配策略，给出了相应的产能比例分配模型，得到了最优的产能分配策略，并证明了模型解的存在性和对模型进行了求解，同时给出了相应的算例验证了其可靠性。但在实际情况中，产品的需求不一定服从均匀分布，还可能服从其他随机分布，因此本文的模型具有一定的局限性。同样，对于不确定需求条件下，小型制造企业同时生产两种以上的多产品的有限产能分配决策问题，将是下一步研究工作的方向。

[1] Reyes P.M.. A mathematical example of the two-echelon inventory model with asymmetric market information [J]. Applied Mathematics and Computation,2005,162(1):257-264.

[2] Ji X. , Shao Z.. Model and algorithm for bilevel newsboy problem with fuzzy demands and discounts[J]. Applied Mathematics and Computation,2006,172(1):163-174.

[3] 陈炜婷，龚锡挺，王其文. 订单驱动生产系统产能分配与订单接受优化决策[C]. 第三届(2008)中国管理学年会论文集,2008.

[4] 范志宁.协议销售和自由销售并存情况下共用产能分配策略研究[J]. 科学技术与工程,2011,11(7):1644-1648.

[5] 刘浪，陈建宏，郑海力. 模糊预测型线性规划在矿山产能分配中的应用[J]. 中南大学学报(自然科学版), 2012,43(2):613-618.

[6] Tang Q., Musa S.N.，Li Z.. Dynamic pricing in the newsvendor problem with yield risks[J].International Journal of Production Economics,2012,139(1) :127-134.

[7] Ho J.W., Fang C.C.. Production capacity planning for multiple products under uncertain demand conditions[J]. International Journal of Production Economics ,2012, 141(2): 593-604.

[8] Chan L.M.A., Simchi-Levi D., Swann J.. Pricing, Production, and Inventory Policies for Manufacturing with Stochastic Demand and Discretionary Sales[J]. Manufacturing & Service Operations Management, 2006, 8(2):149-168.

[9] Feng Y., Xiao B.. Integration of pricing and capacity allocation for perishable products [J]. European Journal of Operational Research,2006,168(1) :17-34.

[10] Hood S.J., Bermon S., Barahona F. Capacity planning under demand uncertainty for semiconductor manufacturing[J]. IEEE Transactionson Semicon-ductor Manufacturing,2003,16(2):273-280.

[11] 曼昆著，梁小民译，经济学原理(第四版)[M]. 北京:北京大学出版社,2006.

[12] Chew E.P., Lee C., Liu R.. Joint inventory allocation and pricing decisions for perishable products[J]. International Journal of Production Economics, 2009, 120(1): 139-150.

(编辑 赵蓉)

Research on the Small Production Enterprise Limited Capacity Allocation Decision under the Condition of Uncertain Demand

HAN Zheng-tao,ZHANG Bi-xi

(College of Management, Guangdong University of Technology, Guangzhou 510520, China)

This paper mainly studied under the condition of considering the limited capacity of small production enterprise capacity allocation decision problem. When a small production enterprise in the face of uncertain demand environment, how to properly allocate appropriate proportion of production capacity to the corresponding product, to prevent unnecessary loss of revenue from the shortage or excess of a product. This paper gives the optimal capacity allocation model for small production enterprise while the demand of two kinds of production follows uniform distribution to maximize profits. And through the existence of solutions of the model and solving process and numerical example verify the reliability of the model.

uncertain demand; small production enterprise; uniform distribution; capacity allocation

1001-2265(2014)06-0135-03

10.13462/j.cnki.mmtamt.2014.06.037

2013-10-01;

2013-12-28

国家自然科学基金项目(71271060，70971026)；广东省自然科学基金项目(S2012010009278，9151009001000045)

韩正涛(1988—)，男，安徽天长人，广东工业大学硕士研究生，研究方向为生产系统组织与优化，(E-mail) zhengtaohan@163.com。

TH16;TG65

A