环境激励下船舶结构模态参数识别方法综述

洪 明 雷 川 崔洪宇

（大连理工大学 船舶工程学院 大连116024）

环境激励下船舶结构模态参数识别方法综述

洪 明 雷 川 崔洪宇

（大连理工大学 船舶工程学院 大连116024）

基于模态分析理论，对环境激励下的模态参数识别方法进行归纳总结，讨论了不同模态参数识别方法的基本思想和优缺点，并着重介绍船舶航行状态下的模态参数识别。文章对国内模态参数识别的研究热点问题进行了阐述，为相关科研人员研究环境激励下模态参数识别提供了有益参考。

环境激励；模态参数识别；船舶结构；运行模态分析

引 言

船舶航行过程中，结构会受到来自螺旋桨、主机及风浪流等激励作用，不可避免地会产生结构振动。船舶振动不仅会影响船上人员生活的舒适性，还会对船上设备及船舶结构自身强度带来危害，因此船舶振动问题逐渐引起人们的重视。

一般的振动问题由激励（输入）、结构（系统）和响应（输出）三部分组成，根据研究目的不同，通常将振动问题分为图1所示三种基本类型。

图1 振动问题分类

振动结构模型可以用三种形式来描述，分别是物理参数模型、模态参数模型和非参数模型［1］。解决振动问题时最为关注的是模态参数模型，它包括结构的模态频率、振型和阻尼比等参数，而模态分析理论就是以振动理论为基础，以模态参数为目标的分析方法。根据模态分析方法的不同，模态分析理论可以分为理论模态分析、实验模态分析（EMA）和运行模态分析（OMA）［2］，由于运行模态分析的应用特点及实施理论难度，近年来基于环境激励下的模态分析方法越来越受到青睐，以下本文主要讨论运行模态。

1 模态参数识别方法

传统的模态参数识别方法，通过在结构上人工施加激励，已知激励和响应，采用信号处理技术计算系统的频响函数或脉冲响应函数，再运用参数识别方法得到系统的模态参数。传统的模态分析方法按识别域的不同可分为频域法和时域法，频域法是以频响函数为基础的参数识别方法，时域法则是以脉冲响应函数或自由振动响应为基础的参数识别方法；按处理各阶耦合模态所用方法的不同，可分为单自由度法和多自由度法，单自由度法基本思想是将具有多阶模态的多自由度系统视作多个单自由度系统进行识别，适用于阻尼小且相邻模态分离较远的系统，多自由度法则是对频响函数曲线上的各共振峰同时拟合，在感兴趣的频带内考虑各阶模态的耦合与相互影响；按照使用激励和响应的数目不同，又可以分为单输入单输出（SISO）、单输入多输出（SIMO）及多输入多输出（MIMO）识别方法，其中SISO属于局部识别方法，SIMO和MIMO属于整体识别方法［3］。

以船舶结构为代表的大型结构物传统实验模态分析方法需要同时已知激励与响应，才能通过构造频响函数对系统参数进行识别，然而实验过程中很难对船体结构施加有效激励。激励过小，能量不足以激起船舶结构的振动；激励过大，容易导致局部结构发生塑性变形等强度问题。由此，基于环境激励的运行模态分析方法显现出优势，仅需要船舶在航行状态测量的振动响应信号，便可识别系统的模态参数。基于环境激励的运行模态分析技术，一方面可识别船体的振动模态，判断其是否与船上激励源发生共振，还可与设计预报结果进行对比，积累预报经验；另一方面可对振动量级过高区域进行分析，得到该区域有害振动的主要频率成分，对比激励源频率可以确定有害振动来源，并可以根据分析得到的模态振型，对振幅较大位置采取减振措施［4］。

2 环境激励下模态参数识别方法概述

基于环境激励模态参数识别方法，按照信号识别域可分为频域法、时域法以及联合时频域法［5］。频域法大多利用经典谱估计，对于输入信号已知的实验状态进行频域模态分析，根据频响函数在系统固有频率峰值特征进行模态识别；基于环境激励下的模态分析，由于无法直接求得频响函数，所以一般使用功率谱密度函数近似地代替频响函数，基于功率谱密度函数进行模态识别的方法主要有峰值拾取法和频域分解法。

时域法属于现代谱分析的范畴，其算法思想大致有两种：第一种直接利用响应信号求系统模态参数，如基于数据的随机子空间法以及ARMA时序分析法；第二种先需要对信号进行处理，配合自然激励技术或随机减量技术，得到中间时间序列如相关函数、近似的自由响应或脉冲响应信号等，然后利用经典时域模态识别方法进行参数识别，如ITD法、最小二乘复指数法、多参考点复指数法、基于协方差的随机子空间法以及特征系统实现法等［6］。

无论频域法还是时域法都是基于傅里叶变换进行模态识别的，但由于傅里叶变换自身不能反映信号的瞬时性即信号在时频域内的变化规律，因此能够在时频域内反映信号能量分布情况的时频分析开始成为学者研究的热点，其中小波变换和Hilbert-Huang变换是最为经典的两种时频分析方法，它们都能够根据信号的时间-尺度特征自适应地对系统进行模态识别，弥补了频域法和时域法在处理非稳态环境信号和非线性系统模态识别的不足，扩展了模态参数识别的应用领域［7］。图2所示为常见的基于环境激励的模态参数识别方法以及模态识别过程中应用到的关键技术，本文将给出这些算法的数学模型和算法思想，并重点阐述这些算法的适用性和优缺点。

图2 环境激励下模态参数识别方法分类

2.1 频域法

2.1.1 峰值拾取法

峰值拾取法［8］的基本思想是系统的频响函数在其固有频率处会出现峰值点，由于环境激励前提为白噪声信号，白噪声信号的功率谱密度函数在一定频率范围内近似均匀分布，因此可以利用输出响应的功率谱密度函数近似代替频响函数。另外该方法假定随机响应的功率谱密度函数峰值仅由一个模态确定，这样系统的固有频率可以由功率谱密度函数的峰值得到，利用识别结果挠度分布就可近似表示模态振型。峰值拾取法的优点是算法简单且识别效率高；缺点是环境激励需满足白噪声特征，且不能识别密集模态和阻尼比，由于对功率谱密度函数峰值选取存在主观性，所以其识别精度受到影响。

2.1.2 频域分解法

频域分解法是峰值法的改进算法，主要用来解决峰值法难以处理密集模态的问题。频域分解法对功率谱密度函数矩阵进行奇异值分解（SVD），将系统响应的功率谱密度函数分解为对应多阶模态的一系列单自由度系统功率谱密度函数，然后利用峰值法识别模态参数。频域分解法是峰值法的一种延伸，它不仅继承了峰值法算法简单、识别效率高的优点，还能识别密集结构的模态参数，而且由于采用了SVD技术，所以对噪声也有一定的抗干扰能力，识别精度较峰值法有所提高。

张毅刚等［9］针对峰值法进行空间网格结构模态参数识别时会遇到遗漏模态及重复频率无法筛选的问题，对峰值法进行了改进，提出在获得所有测点平均正则化功率谱基础上，结合结构的理论振型特点计算辅助正则化功率谱，取两者并集为模态识别结果，通过典型结构监测结果验证了改进后的功率谱峰值法的有效性，图3为实验测得的平均正则化及辅助正则化功率谱密度函数曲线［9］。

图3 平均正则化及辅助正则化功率谱密度函数曲线

夏祥麟［10］对简支梁分别进行了峰值拾取法和频域分解法研究，发现频域分解法在保留了峰值法识别快速直观的基础上，摒除了峰值由单一模态贡献的假定条件，具有一定的抗噪性能，但是对于非白噪声信号及大阻尼系统，频域分解法的识别效果并不准确；Brincker等［11］在频域分解法的基础上对算法进行改进，其基本思想是将分解后的单自由度功率谱密度函数进行逆傅里叶变换，在时域内计算得到相关函数后，利用指数衰减法计算频率和阻尼比，改进后的频域分解法可直接在时域内完成频率和阻尼比的计算，使得对频率的求解不再依赖FFT分辨率的影响。

2.2 时域法

2.2.1 基于原始响应信号的时域法

（1）ARMA时序分析法

1969年Akaike［12］首次使用自回归滑动平均模型进行白噪声环境激励下的模态参数识别。ARMA时序分析法的基本思想是利用差分方程和Z变换，分别建立强迫振动方程传递函数与ARMA模型间等价关系，直接使用随机激励和响应信号，并采用ARMA模型结合最小二乘法来识别系统模态参数。ARMA时序分析法属于SISO参数识别法，用一个测点就可以识别出系统各阶模态参数。ARMA参数模型包括AR自回归模型、MA滑动平均模型和ARMA自回归滑动平均模型。

对确定性系统，系统输入和输出关系为：

该式称为系统的自回归滑动平均模型。式中：ai和bi分别称为自回归系数和滑动平均系数，如果bi= 0，则上式变为即AR自回归模型；如果ai= 0，则即MA滑动平均模型，所以AR模型和MA模型是ARMA模型的两种特殊情形。

ARMA时序分析法不受观测样本长度限制，不存在能量泄露的问题，且识别精度较高；缺点是在建立时序模型时系统的阶次难以确定。郭永刚等［13］利用单位脉冲响应函数与ARMA模型Green函数等价的特点，通过脉冲响应函数来估计系统响应的自相关系数；然后建立推广的Yule-Walker方程以求得ARMA模型自回归系数并进行参数识别，在其算例研究中发现为保证识别结果的精度需建立较高阶数的ARMA模型，但模型阶数过高又会导致识别计算量剧增；Smail等［14］针对基于ARMA模型的模态识别方法系统阶次难以确定的问题，提出利用输出信号相关矩阵特征值个数来确定系统阶次，取得了较好的识别结果。

（2）数据驱动的随机子空间法

数据驱动的随机子空间法是由Overschee等于1991年提出的［15］，算法直接将原始响应数据作为输入部分形成Hankel矩阵，利用QR分解和SVD技术获得扩展的可观测矩阵，并利用卡尔曼滤波状态序列结合最小二乘法识别出系统的模态参数。

数据驱动的随机子空间法相对于协方差驱动的随机子空间法最大区别有两点：一是不需要进行相关函数的计算，提高了算法的识别效率；二是采用QR分解技术，研究表明QR分解能够很大程度上提高随机子空间法的识别精度。辛峻峰等［16］在理论上探讨了协方差驱动和数据驱动两种随机子空间法的不同，并通过相应的数值模拟验证基于QR分解的数据驱动随机子空间法无论计算精度或对较弱势模态的识别能力均明显优于协方差驱动随机子空间法，辛峻峰等［17］还对随机子空间法深入分析噪声与数据驱动的随机子空间法Hankel矩阵维数之间的关系，并提出一种评估随机子空间法矩阵维数选择优劣的方法；常军等［18］就随机子空间法中存在的虚假模态问题进行分析，表明产生虚假模态的原因主要有两方面：一方面是由于随机子空间法的算法本身而导致；另一方面是由于输入信号不满足白噪声假定或者输出信号受到环境干扰而引起；章国稳等［19］针对数据驱动的随机子空间法计算效率低下的问题，提出一种基于特征值分解的随机子空间法，通过模型研究证明该方法在保持计算精度的基础上提高了随机子空间法的计算效率。数据驱动的随机子空间法适用于线性结构平稳激励下的模态参数识别，对输出噪声也有一定的抗干扰能力，但仍不可避免地会遇到虚假模态的问题；此外，状态空间方程中系统阶次的确定是限制所有基于状态空间方程方法运算速度和精度的最主要因素，基于状态空间方程的随机子空间法也存在同样的问题。

2.2.2 基于自由响应或脉冲响应信号的时域法

（1）随机减量技术（RDT）

对于船舶等大型结构物来说，工程实际中容易得到的是随机响应信号，但是很多时域模态识别方法是以自由振动响应为数学模型的，所以需要从随机响应信号中提取出某种自由振动响应信号。RDT法是利用样本平均的方法，通过设置一定的触发条件去除响应中的随机成分，获得初始激励下的自由振动响应，然后通过相应的时域法识别出系统的模态参数。Cole［20］首先提出RDT法，并将其成功应用于空间飞行器模型结构的模态识别；Ibrahim［21］将RDT法同ITD法相结合用于结构运行模态参数的识别，并对RDT法中采用的触发条件进行详细阐述，同时在其论文中强调RDT法仅适用于白噪声激励。由于RDT法建立在线性系统叠加原理的基础上，所以不能用来分析非线性系统；另外RDT法利用了白噪声激励下系统产生的平稳响应方差为零这一特性，所以RDT法仅能用于处理平稳随机信号。

（2）自然激励技术（NExT）

NExT法的基本思想是白噪声环境激励下结构两点间响应的互相关函数和脉冲响应函数有近似的表达式，求得两点间响应的互相关函数后，将其作为输入信号进行模态参数识别。美国SADIA国家实验室的James等［22］在1994年提出NExT法，并且将该方法运用于汽轮机叶片在工作状态下的固有频率和模态阻尼的测试。

对自由度为n的线性系统，当系统k点受脉冲激励时，i点的脉冲响应写成如式（2）所示：

从上式可以发现，i和j两点之间的互相关函数可看成一系列衰减简谐函数的组合，同两点间脉冲响应函数具有相同表达形式，故可将NExT法与基于脉冲响应时域方法结合起来进行模态参数识别。

罗奎［23］分别用NExT结合ITD法以及NExT结合ERA法对环境激励下三跨混凝土连续桥进行振动试验模态参数识别，发现NExT法由于对响应信号进行互相关函数的计算，其对噪声的抗干扰能力较强；纪晓东等［24］综合自然激励技术和特征系统实现算法，进行模拟环境激励下结构的时域模态参数识别，通过改变结构质量和特征灵敏度分析，得到质量归一化振型，通过模型实验验证了NExTERA法能应用于结构在线模态参数识别。

（3）ITD法

ITD法［25］是Ibrahim提出的一种SIMO参数识别方法，基本思想是直接使用各测点的自由响应信号，通过三次不同延时采样，构造自由响应采样数据的增广矩阵，然后建立特征方程，求解出特征对后再估算各阶模态参数，ITD法的最大特点是同时使用全部测点的自由响应数据。Ibrahim在ITD法的基础上提出省时的STD法，STD法相对ITD法的计算量大为降低，节省内存和运算时间，在识别精度上也有所提高。

杨佑发等［26］结合随机子空间法对ITD法进行算法改进，提出将随机子空间法中计算得到Toeplitz矩阵作为输入传递给ITD法，避免使用RDT法和NExT法进行前处理引起的误差，实验表明该改进后ITD算法相对于随机子空间法识别精度没有降低，而且缩短了计算时间，相对于传统的ITD法，识别精度明显有所提高；周凯［27］采用ITD法对环境载荷下一个近海导管架平台结构模型进行模态参数识别，研究发现增多ITD法中虚拟测点的个数，增大特征矩阵的阶数，不仅能增加识别出的模态数量，而且有助于降低其对噪声的敏感度，虚拟测点个数对系统模态识别结果影响如图4所示［27］。

图4 虚拟测点个数对系统模态识别结果影响

（4）最小二乘复指数法（LSCE）和多参考点复指数法（PRCE）

LSCE法［28］又称Prony多项式法，与ITD法相比，LSCE法在识别模态频率和阻尼比时只用一个测点的脉冲响应数据，因而LSCE法属于局部识别法。LSCE法的基本思想是以Z变换因子表示脉冲响应，Z变换因子中包含待识别的复频率，构造Prony多项式，使其零点等于Z变换因子的值，将求解Z变换因子就转化为求解Prony多项式系数：

为求解Prony多项式系数，构造脉冲响应数据序列的自回归模型，自回归系数即Prony多项式系数，通过在不同起始点采样，得到关于自回归系数的线性方程组，用最小二乘法计算得到自回归系数的解，可得Prony多项式的根。再由脉冲响应数据序列构造该测点各阶脉冲响应幅值（留数）的线性方程组，用最小二乘法求解，对各测点作识别，便可得到各阶模态矢量，脉冲响应序列的自回归模型如下：

式中：为以l为起始采样点的含2n个采样值的时序样本，为自回归系数列阵，即Prony多项式的系数。

为克服LSCE法仅能应用于单输出状态的不足，在LSCE法的基础上建立MIMO整体识别的PRCE法［29］，其数学模型为基于MIMO的脉冲响应函数矩阵。

（5）协方差驱动的随机子空间法

其基本思想是由输出响应数据构建Hankel矩阵，计算协方差序列形成Toeplitz矩阵，Toeplitz矩阵主要作用是保持信号原有信息的情况下缩减数据量，然后对其作SVD得到系统矩阵，进而识别结构的模态参数。其同样存在系统阶次难以确定的问题，无论是根据非零奇异值点个数或是利用奇异值的跳跃都难以在实际工程中确定系统的阶次，目前一般采用随机子空间结合稳定图的方法进行模态参数的识别［30］，稳定图是目前普遍认可的相对较好的确定系统阶次的方法［31］。

（6）协方差驱动的随机子空间法特征系统实现法（ERA）

特征系统实现算法是美国航天航空局的Langley研究部门于1984年提出的一种时域模态分析方法［32］。ERA法以由MIMO得到的脉冲响应函数为基本模型，利用结构的脉冲响应信号函数矩阵来构建广义Hankel矩阵，对其进行SVD，从非零奇异值中提取得到系统的特征量，通过对系统矩阵进行特征值分解识别出系统的模态参数。因其在计算中利用了最小实现原理，大幅度减小矩阵维数和计算量，在实际工程中应用十分广泛。

ERA法通常结合NExT法用来识别环境激励（白噪声激励）下的系统模态参数，NExT-ERA法程序流程图如下页图5所示。许俊臣和洪明［33］利用NExT-ERA法对一钢质船体梁模型进行了模态参数识别，如图6 -图8［33］所示。

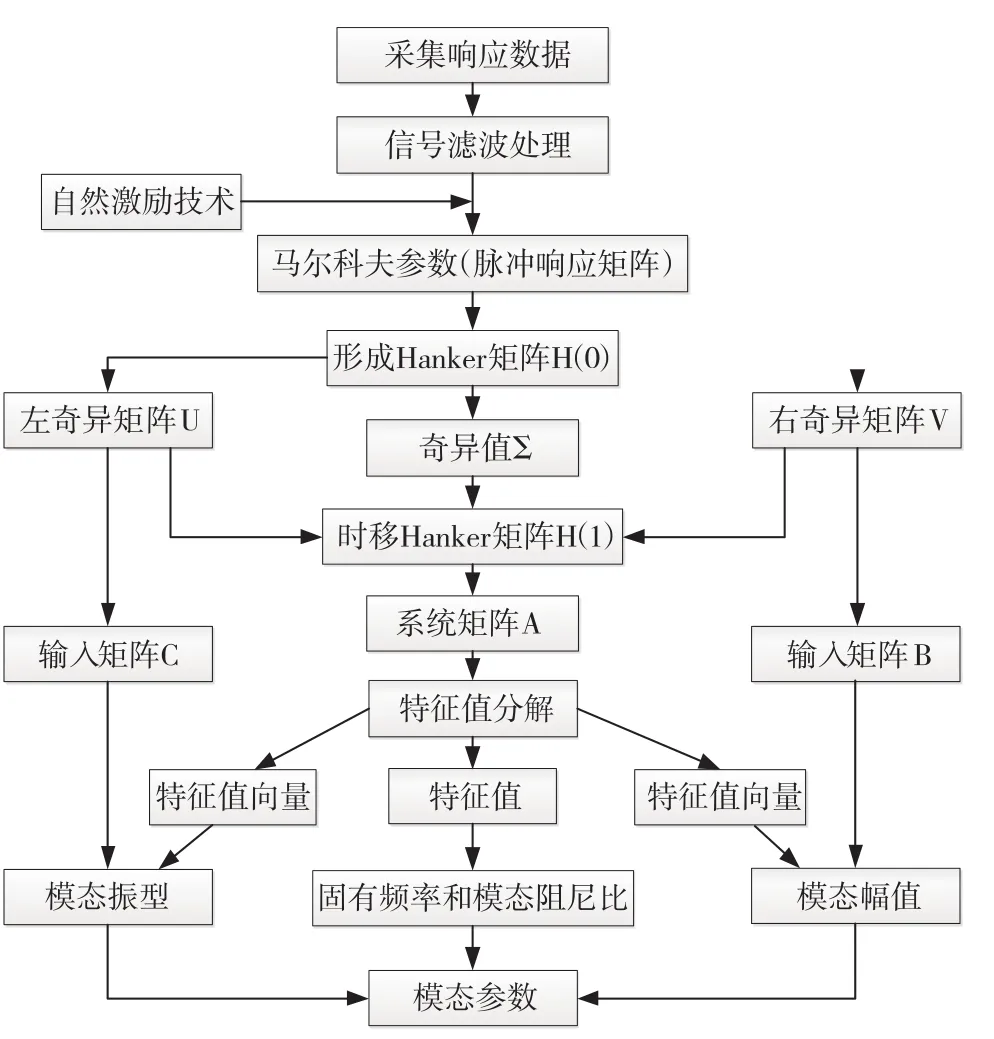
图5 NExT-ERA法程序流程图

图6 船模结构示意图

图7 水池船模结构实验图

图8 稳态白噪声激励下的系统稳定图

研究中对存在单频激励时对应的简谐频率的影响，信噪比的影响以及在不同装载情况下的船模模态参数进行大量的实验对比和系统的分析研究。实验结果显示只要简谐激励的频率与固有频率没有离得太近，其频率和信噪比对模态分析的影响不大，当两者频率较为接近，可能会发生频率混叠的现象；局部结构上附加质量的存在对局部模态振型和识别结果会造成一定影响；万岭和洪明等人［34］采用NExT-ERA法对简支梁模型和船体模型分别进行模态参数识别，验证了NExT-ERA法进行运行模态识别能够得到良好效果。文章对ERA法中系统阶次的确定进行深入讨论，指出选择较低阶次容易丢失系统的模态信息，而选择较高阶次又会引入噪声模态；杨和振、李华军等人［35］采用NExT-ERA法对海洋环境载荷下海洋平台结构模拟模型进行了参数识别，并将识别结果同峰值法进行比较，比较结果显示NExT-ERA法更加适用于环境激励下大型结构物的模态参数识别。

2.3 联合时频域法

2.3.1 小波变换法

小波变换是一种基于信号时间-尺度的分析方法［36］，具有多分辨率分析的特点，即在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，在时域和频域都具有表征信号局部特征的能力，很适合探测正常信号中夹带的瞬态反常现象，因此被广泛地应用于对非平稳信号的分析和处理中［37］。

对于一个自由度为n的线性系统，其自由振动响应可以表示为：

对上式进行小波变换可以得到：

式中：a和b分别称为小波变换的尺度参数与位移参数。

当尺度参数为ai时，在小波变换过程中，只有与ai相关的模态起主要贡献，其余的模态可以忽略不计，则有：

由上式可以分别得到其幅值和相位值：

通过上式便可以识别出系统的模态参数。小波分析自身也存在一定的局限性，对具体信号依据何种原则来选择小波基，目前在理论上和实际应用中尚没有统一的方法，而且小波变换还可能由于其有限长度的特点出现能量泄露等问题，另外，小波变换的实质是一种线性变换，不能用于处理非线性问题。

朱宏平等［38］针对土木工程结构前几阶自振频率处于低频区域以及环境激励下结构响应信号信噪比很低的特点，着重论述采用小波方法抑制原始测量信号中的高频噪声部分，从而突出结构低频特性的基本原理，并用其对一实际高层结构进行模态参数识别，识别结果显示基于小波变换的模态分析方法较传统模态分析方法识别精度更高更有效。邵艳秋［39］采用RDT法获得环境激励下结构的自由响应，通过改进的Morlet小波时频分析，分解多自由度系统为若干个单自由度系统的组合，根据小波系数和系统固有频率和阻尼比间关系识别出环境激励下结构模态参数，并应用GARTEUR模型验证小波变换方法的有效性；李夕兵等［40］分别应用小波变换和HHT变换对实测爆破震动信号进行时频分析，发现HHT较小波变换避免了选择小波基的困难，在分析非平稳信号时更具适应性，而且小波谱由于受小波基有限长度及测不准原理的限制，容易造成频谱扩散和能量泄露的问题。

2.3.2 Hilbert-Huang变换法

HHT作为一种针对非线性系统非平稳信号的自适应时频处理方法，由Huang等人于1998年首次提出［41］。HHT主要由经验模态分解（EMD）和希尔伯特变换（HT）组成。经验模态分解是处理时域信号的方法，可将初始信号分解成一系列本征模态函数（IMF）和残余项的叠加，实现对原信号的强制平稳化处理，其中分解得到的IMF分量能够表征信号在某一特征尺度上的振动模态；然后根据Hilbert变换，可以完成瞬时模态参数的求解（主要指瞬时频率），其算法流程如图9所示。

图9 HHT算法流程图

相对于传统的时域模态参数识别方法，HHT将参数识别扩展到时频域范围，打破了传统方法基于傅里叶变换只能在频域或时域描述信号的缺陷，提出了瞬时频率的概念，能够用来解决非稳态环境下的模态参数问题；相对于小波变换方法，Hilbert谱在时频域的分辨率都要高于小波谱，具有更强的局部特性，而且能够反映系统的非线性特性。但是对基于HHT的模态识别方法的研究也存在很多不足，其理论推导并不完善，对特定信号容易出现端点效应，尤其对于模态频率较为接近的结构容易发生模态混淆的现象。

姚熊亮和张阿漫［42］基于EMD对水下爆炸结构冲击信号进行分析，通过研究每一个本征模态函数，从本质上分析了水下爆炸冲击加速度信号的组成成分及特点；陈隽和徐幼麟［43］结合青马桥的实测动力响应，研究了HHT方法在结构模态参数识别中的应用，并将其分别用于平稳和非平稳的实测记录以识别结构的模态信息，验证了HHT相对传统模态识别方法在处理非平稳性数据方面具有明显优势；汤宝平和何启源等人［44］为克服噪声信号对EMD分解的影响，提出基于小波去噪和HHT相结合的模态参数识别方法，该方法先利用小波进行信号去噪，以减少EMD分解过程的计算量和分解层数，然后利用HHT进行模态参数的识别，简支梁系统实验证明该算法对阻尼的识别精度明显提高；韩建平和李达文［45］针对传统模态识别方法对非线性和非稳态信号处理能力差，且对阻尼比识别精度较低的现象，采用基于NExT和HHT相结合运行模态参数识别方法，通过对一个12层钢筋混凝土框架模型进行模态分析，验证了这种算法对阻尼比的识别效果较传统基于傅里叶变换的半功率带宽法有所改进，但对识别精确性仍难以确认；刘晓冰［46］采用基于NExT和HHT相结合运行模态参数识别方法，对船模结构进行了模态识别研究，验证了该方法有效避免NExTERA法中的虚假模态和系统定阶问题，适用于船舶结构参数识别及状态监测。

3 环境激励下模态参数识别研究热点

3.1 复杂密频结构的模态参数识别

传统的模态参数识别方法，普遍要求被测结构的各阶模态频率较分散，阻尼比较小，即模态混叠不严重，但是对于工程中的大型复杂结构，特别是具有质量或刚度突变的结构，普遍含有密集模态，难以通过激振使结构按某一阶固有振型振动。产生密集模态的原因有两个：一是各阶模态的固有频率过于靠近；二是模态阻尼比较大。如果两个模态的固有频率很接近，且各自的阻尼比也较大，则在频谱上会出现如图10［49］所示的模态混叠现象，无法用普通的傅里叶带通滤波来实现对多模态的分离，进而影响多模态参数识别的精度。

图10 模态混叠示意图

传统的基于傅里叶变换的模态识别方法不能直接用来识别复杂密频结构，因此时频分析方法被更为广泛地应用于密集模态结构的模态识别。陈隽等［47］采用HHT法对密频结构的阻尼进行识别，对两个自由度的密频和非密频结构分别采用HHT法和半功率带宽法进行参数识别，结果表明HHT法对密频结构模态识别的识别精度明显优于半功率带宽法，但是HHT法对密频结构的识别精度随频率密集度的提高而明显降低，为解决密频结构的模态混叠问题，作者选择采用在EMD分解过程中引用一种称为间歇检测准则的方法来消除混合现象；刘俊斐和李华军［48］结合海洋平台物理模型的动力响应数据，采用加入伪信号技术的HHT方法对模态密集结构进行模态分析，并对加入伪信号的幅值和频率选择进行改进，进而使用峰值法和HHT法结合伪信号技术对力锤激励下的海洋平台物理模型进行模态参数识别，得到结构的自振频率和阻尼比；黄应来和董大伟等人［49］提出了一种针对密集模态结构模态参数识别的方法，其基本思想是先用EMD分解化多模态参数识别问题为单模态参数识别问题，考虑到适当减小各阶模态的阻尼比可以相应降低各阶模态间的混叠程度，采用加逆衰减指数窗与带通滤波相结合的方法，将各个模态近似提取出来，再使用先进的时频分析方法识别系统模态参数。图11［49］和图12［49］分别为密集模态结构加速度响应信号加逆衰减指数窗前后的时域图和频谱图。

图11 加逆衰减指数窗前后时域图

图12 加逆衰减指数窗前后时域图

可以看出，通过加入适当的逆衰减指数窗，可以有效降低模态密集度，利用带通滤波器就可以将多模态信号中的各阶模态分离出来，然后利用Hilbert变换等方法识别系统的模态参数；曹军宏和庄飚等人［50］提出采用基于时延优化的二阶盲辨识算法对模态密集结构进行参数识别，其基本思想是利用量子遗传算法对二阶盲辨识算法中时延的选择进行优化，并对观测信号的最优时延二阶协方差矩阵作对角化处理，同时得到模态振型和单自由度信号，然后基于FFT法提取出对应各阶模态的模态频率和阻尼比；孙鹏和丁幼亮等人［51］从小波变换公式推导的角度对结构模态混叠的机理进行研究分析，明确密集模态的定义并给出结构模态密集度指标，即相邻模态的频率比，研究表明当相邻模态的频率比一定时，随着阻尼比以及相邻模态阻尼比差值的增加，模态混叠现象会愈加严重。

3.2 非稳态环境激励下的模态参数识别

频域法和时域法中假设环境激励需要近似表示为平稳白噪声激励，这是因为频域法和时域法都建立在傅里叶变换的基础上，而傅里叶变换的全局特性限制其不能够用来分析非平稳信号。对于船舶等大型水上结构，通常将环境激励特征归纳为平稳的强线谱与弱随机谱的叠加，这也是对船舶环境激励的一种简化或者近似，真实的环境激励应当多为非稳态的信号。常军等［52］对随机子空间法产生虚假模态和模态遗漏现象的原因进行深入分析，发现产生虚假模态的主要原因是由于输入信号不满足白噪声假设，并由此提出分段平稳随机信号参数识别方法；李爱群等［53］在润扬大桥的健康监测中发现在风荷载及车辆荷载下大桥的动力响应在一定的时间尺度内是非平稳的，不满足传统模态参数识别方法的白噪声假设，因此以HHT和小波变换为代表的联合时频域法成为分析非稳态环境激励下模态参数识别的主要手段。

李中付和华宏星［54］认为任意随机激励信号都可以表示成白噪声和非白噪声信号的叠加，其一般形式写作：

由此，我们可推导出线性系统响应之间的相关函数由两部分组成，一部分与脉冲响应具有相同的数学形式，另一部分为其他形式；然后基于EMD分解，把非稳态环境激励下多自由度线性系统的模态参数辨识问题转化为类似于已知各个单自由度系统的脉冲响应进行参数辨识问题。这种算法主要有两个优点：一是无论白噪声激励、稳态随机激励还是非稳态随机激励，都可以仅根据结构的响应识别出线性结构的模态参数；二是能够有效地识别出环境激励中的周期成分。

Chiang和Lin［55］假设外部激励是由平稳白噪声信号和一个调幅信号乘积组成新的非平稳随机信号，他证明在这种假设条件下测得的响应历程的均方根函数中包含了激励信号中的调幅成分，并可以通过曲线拟合将调幅信号提取出来，这样就可以将非平稳信号转变为平稳信号，然后计算不同测点间响应信号的互相关函数，得到的信号便是一个可以进行模态识别的自由衰减信号。作者使用ITD法对其进行模态识别，并用一个六自由度的链式结构进行数值实验对该方法进行验证。向律楷［56］在文章中将环境激励由白噪声扩展到MA（q）阶模型，假设非平稳激励由d-1阶多项式趋势项与MA（q）阶模型之和构成，并使用NExT-ERA法识别出系统的模态参数。杜秀丽和汪凤泉［57］将环境激励视作均匀调制的莱维随机激励，并基于连续时间AR模型提出时域模态分解方法，数值实验证明该算法能够精确识别满足这种激励模型下的系统模态参数。

本文基于EMD分解，对非稳态环境激励下的三自由度系统进行模态参数识别，具体参数如式（13）-式（15）所示：

式中：m为模型质量，kg；k为刚度，N/m；c为阻尼，N·s / m。

分别对2号质点施加四种不同形式的激励：平稳白噪声信号、平稳白噪声加简谐信号、平稳白噪声加线性调频信号（频率从0到30 Hz随时间线性增加）以及平稳白噪声和调幅信号（e-0.1t）的乘积，采样频率为500 Hz，采样时间为30 s，用Newmark法求得三个质点的加速度响应，分别对任意两点做互相关，然后对得到的互相关函数进行EMD分解，并用Hilbert变换得到该三自由度结构在四种不同激励下的模态参数，识别结果如下页表1所示。由识别结果所示，说明该算法不仅能够识别稳态环境激励下的系统模态参数，且可正确识别出各种不同形式非稳态环境激励下的系统模态参数。

3.3 时变系统的模态参数识别

目前针对船舶结构的模态参数识别主要是将其视作线性时不变系统来进行识别，但视作线性时变系统更合理，这时传统的运行模态分析方法便不再适用。然而目前对线性时变结构的模态识别研究，也多是将线性时不变结构参数识别理论基于“冻结时间”思想的直接推广，即假设每一时刻的时间被瞬间“冻结”，这样结构就变为时不变结构，然后按时不变结构参数识别理论识别出每一时刻的模态参数，再用曲线拟合得到随时间变化的模态参数［58］。李雷［59］提出一种基于“短时时不变假设”结合工况模态分析的识别方法，对飞行器舵片模型进行模态辨识，分析得到舵片模型在受热情况下动力学参数的时变规律。但是这种做法忽略了结构参数随时间变化给结构动力特性带来的影响，造成某些情况下的分析结果不符合实际，因此这种模态参数一般被称为“伪模态参数”［7］。

表1 四种不同工况下模态参数识别结果

为了准确描述时变系统模态参数随时间变化的特性，以HHT和小波变换为代表的联合时频域法被更多地应用到时变系统的模态参数识别过程中。刘建军［60］提出基于HHT由线性时变SDOF结构的自由振动响应识别结果模态参数的新方法，并将其扩展到了MDOF结构及强迫振动条件下结构的模态识别，并用可调附加质量的悬臂梁实验验证HHT用于识别时变系统模态参数的有效性；宋斌华［61］在刘建军工作基础上研究HHT和LMD［62］两种新的时频分析方法在时变结构模态参数识别中的应用；沈林［63］基于Daubechies小波对线性时变系统进行物理参数识别，并对线性时变系统在参数连续平滑变化、周期变化和突变的工况下进行仿真算例研究，验证了Daubechies小波能够正确有效地识别时变系统的物理参数。

我们基于HHT变换对一刚度和阻尼随时间连续变化的两自由度线性时变系统进行数值模型研究，采样频率为500 Hz，采样时间为3 s，该数值模型的具体参数分别取为：

式中：m为模型质量，kg；c为阻尼，N·s / m；k为刚度，N/m 。

将算例中的质点m1在t = 0时刻拉离平衡位置2mm，另一个质点保持不动，然后从静止自由释放，计算质点m1的加速度响应，对其作EMD分解，并对包含系统单阶模态的瞬态响应分量作Hilbert变换，识别出系统的模态瞬时频率和阻尼比，识别结果如图13、图14所示。

图13 模态瞬时频率识别结果

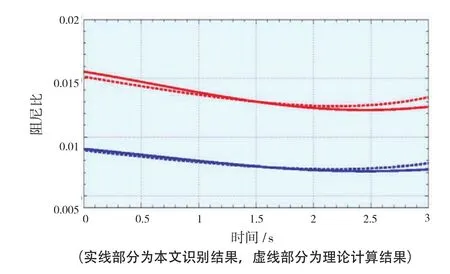
图14 模态阻尼比识别结果

在前面两自由度时变系统数值实验的基础上，本文对一移动质量-悬臂梁耦合时变系统进行实验研究，实验模型如图15所示。

图15 移动质量-悬臂梁耦合系统实验模型

将基于HHT变换的识别结果同传统的特征系统实现法识别结果及有限元分析结果进行研究对比，验证了HHT变换不但可以识别出线性时不变结构的模态信息，而且能够准确地识别得到时变结构的模态参数，识别结果如图16、图17所示。

图16 一阶模态频率识别结果

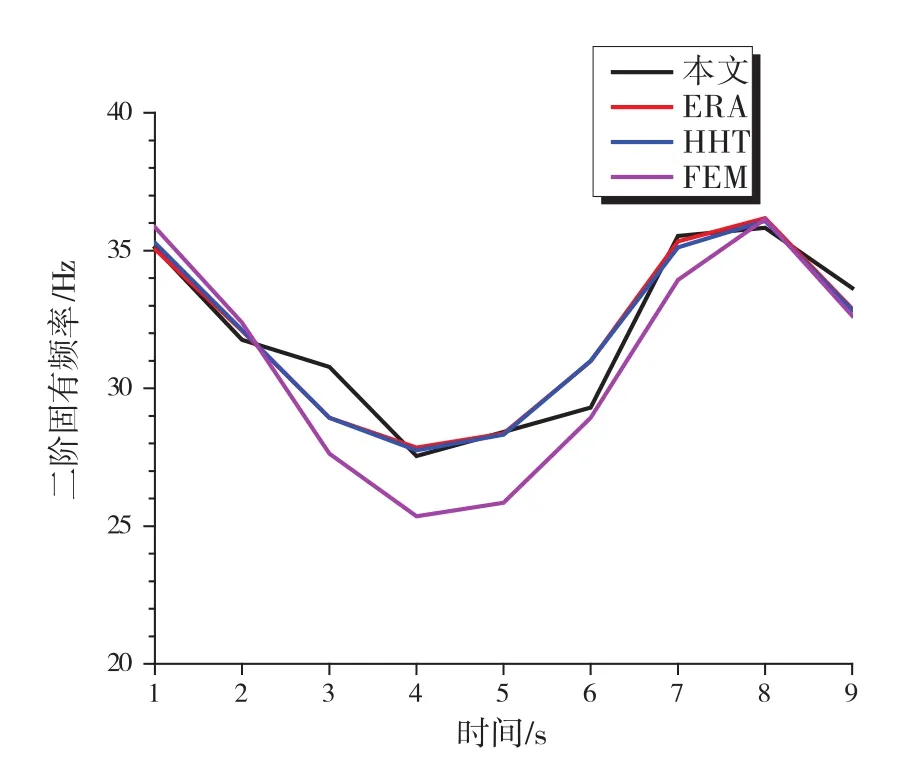
图17 二阶模态频率识别结果

3.4 非线性系统的模态参数识别

非线性模态参数的概念最早由Rosenberg提出，他将模态分析思想扩展至非线性系统领域，Rosenberg给出描述非线性系统模态的频响函数模型，并基于系统的响应数据通过曲线拟合的方法识别出系统的非线性模态参数［64］，其典型特征有两个：一是非线性系统激励与响应之间的关系无法事先确定，必须选择正确的动力学模型对非线性系统进行描述；二是非线性系统的固有频率及阻尼比等模态参数都是时间的函数，因此能够用来刻画系统模态参数随时间变化规律的联合时频域法成为分析非线性系统模态参数的最主要手段。张也弛［65］综合HHT和CxA方法，对强非线性系统进行了模态参数识别，同时指出这种算法能够准确对非线性系统进行模态识别的前提是动力学模型能够真实描述原物理过程；刘卫华等［66］建立了含非线性参数单自由度振动系统的力学模型，如图18所示，系统运动微分方程可写成：

图18 非线性单自由度系统力学模型

式中：α为弱非线性系数。

研究将已知非线性系统产生的混沌响应作为系统激励，并假定该响应由若干个不稳定周期轨道组成，从混沌响应的状态空间中提取出近似周期轨道，并采用谐波平衡法识别出非线性系统的模态参数；针对目前非线性系统模态参数识别的研究主要停留在稳态环境激励下进行，王凤利和赵德有［67］提出非稳态环境激励下基于局域波法的非线性系统模态参数识别方法，算法思想是通过局域波分解得到等效线性系统，并通过Hilbert变换识别出转子系统的模态参数。尽管已有很多学者开始致力于研究非线性系统的模态参数识别方法，但对非线性系统的模态分析还远没有达到线性模态理论研究那样深入和透彻。

4 结 论

本文对环境激励下的模态参数识别方法进行了归纳分类，重点分析这些经典模态识别算法的理论思想和适用条件。主要对目前国内研究热点问题进行了综述，并从数值算例和实验的角度对这些问题进行了分析，为研究和应用提供参考。通过上面对国内相关文献进行分类总结，本文关于环境激励下模态参数识别的研究现状有如下结论：

（1）对于环境激励，目前普遍需要将激励信号视作白噪声或适当宽松地视为平稳信号，即使在部分分析非稳态环境激励的文献中也是将非稳态环境激励近似看成一种固定的表达形式，但是，在实际工程应用中存在的激励信号是任意形式的非平稳信号，如何正确地给出环境激励的近似表达形式尚待研究。

（2）如何从实验模态中有效地甄别和提取噪声模态，尤其对于运行状态下的船舶结构，环境激励包括近似白噪声激励、有害噪声以及船上螺旋桨主机引起的单频简谐激励等，如何考虑这些简谐激励和噪声模态给船舶结构模态分析带来的影响？也是目前可以研究的一个新方向。

（3）不同于实验模态分析，环境激励下的运行模态分析很可能会出现激励不够充分的现象，从导致部分阶次的模态难以识别，因此在实验过程中如何对结构物正确施加激励？也是工程实际中需要考虑的问题。

（4）目前对环境激励下的结构模态参数识别尚没有一种统一完备的方法，各种方法都在一定程度存在缺陷，频域法和时域法不能够用来分析非平稳信号，且存在由噪声引起的虚假模态问题，小波分析不能解决非线性问题且存在分辨率无法保证和能量泄露等问题，而HHT法中针对瞬时频率的数学定义在信号处理领域尚未达成共识，IMF分量之间的正交性也没有完整的数学证明，且存在虚假模态和端点效应等问题。

（5）模态识别过程中对系统阶次确定是十分关键和棘手的问题，尽管已经有学者提出采用模态置信度及稳定图法来确定系统阶次，但噪声模态的影响仍不能做到完全消除，识别精度还有待改善。

（6）目前对系统固有频率已能准确识别，但是对结构阻尼的识别效果往往不好，仍是亟待解决的问题。

［1］ 曹树谦，张文德，萧龙翔.振动结构模态分析［M］.天津：天津大学出版社，2001.

［2］ 万岭.环境激励下的船舶结构模态参数识别［D］.大连：大连理工大学，2010.

［3］ 姜大正.环境激励下船舶结构模态分析实验与理论研究［D］.大连：大连理工大学，2009.

［4］ 许俊臣.船舶加筋结构的运行模态分析及动力减振优化［D］.大连：大连理工大学，2013.

［5］ 续秀忠，华宏星，陈兆能.基于环境激励的模态参数辨识方法综述［J］.振动与冲击，2002（3）：1-5.

［6］ 刘宇飞，辛克贵，樊健生，等.环境激励下结构模态参数识别方法综述［J］.工程力学，2014（4）：1-5.

［7］ 王学敏.基于Hilbert-Huang变换的桥梁监测信号分析与处理和时变模态参数识别［D］.长沙：中南大学，2008.

［8］ Roeck G De，Peeters B，Ren W X. Benchmark Study on System Identification through Ambient Vibration Measurements［C］. Proceedings of the 18th International Modal Analysis Conference（IMAC），2000：1106-1112.

［9］ 张毅刚，刘才玮，吴金志，等.适用空间网格结构模态识别的改进功率谱峰值法［J］.振动与冲击，2013（9）：10-15.

［10］ 夏祥麟.环境激励模态分析方法的比较［D］.长沙：中南大学，2013.

［11］ Brincker R，Zhang Ling-mi，Andersen P. Modal Identification from Ambient Responses Using Frequency Domain Decomposition［C］. Proceedings of the 18th International Modal Analysis Conference（IMAC），2000：625-630.

［12］ Akaike H. Power Spectrum Estimation Through Autoregressive Model Fitting［J］. Annals of the Institute of Statistical Mathematics，1969，21：407.

［13］ 郭永刚，许亮华，水小平.基于脉冲响应数据的ARMA法建模以及模态参数识别［J］.地震工程与工程振动，2006（5）：167-171.

［14］ Smail M，Thomas M，Lakis A A.Assessment of Optimal ARMA Model Orders for Modal Analysis［J］.Mechanical Systems and Signal Processing，1999（5）：803-819.

［15］ Van Overschee P，De Moor B. Subspace Algorithms for the Stochastic Identification Problem［C］. Proceedings of the 30th IEEE Conference on Decision and Control，1991，1321-1326.

［16］ 辛峻峰，王树青，刘福顺.数据驱动与协方差驱动随机子空间法差异化分析［J］.振动与冲击，2013（9）：1-5.

［17］ 辛峻峰，盛进路，张永波.数据驱动随机子空间法矩阵维数选择与噪声问题研究［J］.振动与冲击，2013（16）：152-157.

［18］ 常军，张启伟，孙利民.随机子空间产生虚假模态及模态遗漏的原因分析［J］.工程力学，2007（11）：57-62.

［19］ 章国稳，汤宝平，孟利波.基于特征值分解的随机子空间算法研究［J］.振动与冲击，2012（7）：74-78.

［20］ Cole H A. On-Line Failure Detection and Damping Measurement of Aerospace Structures by the Random Decrement Signatures［J］.1973，NASACR-2205.

［21］ Ibrahim S R. Efficient Random Decrement Computation for Identification of Ambient Responses［C］.Proceedings of the 19th IMAC，Florida，USA，2001：1-6.

［22］ James G H，Came T G，Edmunds R S. STARS Missile-Modal Analysis of First-Flight Data Using the Natural Excitation Technique［C］. Proceedings of the 12th International Modal Analysis Conference（IMAC），1994.

［23］ 罗奎.基于自然激励技术的结构模态参数识别应用研究［D］.武汉：武汉理工大学，2010.

［24］ 纪晓东，钱稼茹，徐龙河.模拟环境激励下结构模态参数识别试验研究［J］.清华大学学报，2006（6）：769-772.

［25］ Ibrahim S R，Mikulcik E. A Method for the Direct Identification of Vibration Parameters from the Free Response［J］.The Shock and Vibraton Bulletin，1977（4）：183-198.

［26］ 杨佑发，李帅，李海龙.环境激励下结构模态参数识别的改进ITD法［J］.振动与冲击，2014（1）：194-199.

［27］ 周凯.虚拟测点对ITD法识别结果的影响［J］.中国水运，2009（2）：184-186.

［28］ Brown D L，Allemang R J，Zimmerman R，et al. Parameter Estimation Techniques for Modal Analysis［J］. SAE Paper，No.790221，SAE Trans.，1979（1）：828-846.

［29］ Vold H，Rocklin G T. The Numerical Implementation of a Multi-input Modal Estimation Method for Minicomputers［C］. Orlando，FL，USA：Proceedings of the 1st International Modal Analysis Conference（IMAC），1982：542-548.

［30］ 常军，张启伟，孙利民.稳定图方法在随机子空间识别模态参数中的应用［J］.工程力学，2007（2）：39-44.

［31］ Ibrahim S R. Computation of Normal Modes from Identified Complex Modes［J］.AIAAJOURNAL，1982（3）：446-451.

［32］ Juang J N，Pappa R S.An Eigensystem Realization Algorithm（ERA）for Modal Parameter Identification and Model Reduction［J］.NASA/JPL，1984（5）：620-627.

［33］ Xu Junchen，Hong Ming，Liu Xiaobing. Operational Modal Analysis of a Ship Model in the Presence of Harmonic Excitation［J］. J. Marine Sci. Appl.，2013（1）：38-44.

［34］ 万岭，洪明，许俊臣.基于NExT/ERA方法缓解激励下的船体结构模型总体模态参数识别［J］.船舶力学，2013（7）：774-784.

［35］ 杨和振，李华军，黄维平.海洋平台结构环境激励的实验模态分析［J］.振动与冲击，2005（2）：129-132.

［36］ Grossmann A，Morlet J. Decomposition of Hardy Function into Square Integrable Wavelet of Constant Shape［J］. SIAM J. of Math，Anal，1984（4）：723-736.

［37］ 谭冬梅，姚三，瞿伟廉.振动模态的参数识别综述［J］.华中科技大学学报，2002（3）：73-78.

［38］ 朱宏平，翁顺.运用小波分析方法进行结构模态参数识别［J］.振动与冲击，2007（4）：1-5.

［39］ 邵艳秋.环境激励下系统模态参数识别方法研究［D］.南京：南京航空航天大学，2008.

［40］ 李夕兵，张义平，刘志祥，等.爆破震动信号的小波分析与HHT变换［J］.爆炸与冲击，2005（6）：528-534.

［41］ Huang N E，Zheng S，Steven R L. The empirical mode decomposition and the Hilbert spectrum for nonlinear random-stationary time series analysis［C］.Proc R Soc London Ser A，1998，454：903-95.

［42］ 姚熊亮，张阿漫.经验模态分解方法在结构冲击信号分析中的应用［J］.中国舰船研究，2006（4）：11-15.

［43］ 陈隽，徐幼麟. HHT方法在结构模态参数识别中的应用［J］.振动工程学报，2003（3）：383-388.

［44］ 汤宝平，何启源，蒋恒恒，等.利用小波去噪和HHT的模态参数识别［J］.振动、测试与诊断，2009（2）：197-200.

［45］ 韩建平，李达文.基于Hilbert-Huang变换和自然激励技术的模态参数识别［J］.工程力学，2010（8）：54-59.

［46］ 刘晓冰.基于HHT方法船舶结构运行模态参数识别［D］.大连：大连理工大学，2014.

［47］ 陈隽，徐幼麟，李杰. Hilbert-Huang变换在密频结构阻尼识别中的应用［J］.地震工程与工程振动，2003（4）：34-42.

［48］ 刘俊斐，李华军.HHT方法在模态密集结构模态参数识别中的应用研究［J］.中国海洋大学学报（自然科学版），2007（S2）：181-188.

［49］ 黄应来，董大伟，闫兵.密集模态分离及其参数识别方法研究［J］.机械强度，2009（1）：8-13.

［50］ 曹军宏，庄飚，韦灼彬.时延优化二阶盲辨识应用于密集模态结构参数识别［C］.第22届全国结构工程学术会议论文集（第1册），2013.

［51］ 孙鹏，丁幼亮，张劲泉，等.基于Morlet小波变换的结构密集模态参数识别［J］.东南大学学报，2012（2）：339-345.

［52］ 常军，孙利民，张启伟.一种分段平稳随机信号的参数识别方法［J］.振动与冲击，2007（6）：17-20.

［53］ 李爱群，丁幼亮，费庆国，等.润扬大桥斜拉桥模态频率识别的环境变异性［J］.东南大学学报，2007（2）：245-250.

［54］ 李中付，华宏星，宋汉文，等.非稳态环境激励下线性结构的模态参数辨识［J］.振动工程学报，2002（2）：139-143.

［55］ Chiang D Y，Lin C S. Identification of Modal Parameters from Nonstationary Ambient Vibration Data Using Correlation Technique［J］. AIAA Journal，2008（11）：2752-2759.

［56］ 向律楷.非平稳环境激励下大桥结构的模态参数识别［D］.北京：清华大学，2009.

［57］ 杜秀丽，汪凤泉.非平稳环境激励下模态参数识别的连续时间AR方法［J］.中国科学，2009（10）：1736-1742.

［58］ 于开平，邹经湘，庞世伟.结构系统模态参数识别方法研究进展［J］.世界科技研究与发展，2005（6）：22-30.

［59］ 李雷.工况模态分析在时变航天器结构中的应用［D］.上海：复旦大学，2011.

［60］ 刘建军. Hilbert-Huang变换及其在线性时变结构模态参数识别中的应用［D］.长沙：中南大学，2007.

［61］ 宋斌华.基于Hilbert-Huang变换和局部均值分解的时变结构模态参数识别［D］.长沙：中南大学，2009.

［62］ 程军圣，张亢，杨宇，等.局部均值分解与经验模式分解的对比研究［J］.振动与冲击，2009（5）：13-16.

［63］ 沈林.基于小波方法的线性时变系统参数识别［D］.南京：南京航空航天大学，2006.

［64］ Rosenberg R M. Normal Mode in Nonlinear Dual Mode Systems［J］. J Appl Mech，1960，27：263-268.

［65］ 张也弛.基于Hilbert-Huang变换的非线性系统参数辨识［D］.哈尔滨：哈尔滨工业大学，2008.

［66］ 刘卫华，丁旺才，田海勇.混沌激励下振动系统的非线性参数识别［J］.振动与冲击，2009（5）：80-83.

［67］ 王凤利，赵德有.基于局域波法的非线性系统模态参数识别研究［J］.大连理工大学学报，2011（1）：56-60.

Review of modal identifi cation of ship structure based on ambient excitation

HONG Ming LEI Chuan CUI Hong-yu
(School of Naval Architecture, Dalian University of Technology, Dalian 116024, China)

Based on the theory of modal analysis, this paper summarizes the modal identifi cation methods under ambient excitation, and discusses fundamental concepts and the advantages and disadvantages of these methods. It especially introduces the modal parameter identifi cation of ship structure under the ship sailing condition and hot issues about its domestic researches, which provide benefi cial references for the relevant researchers.

ambient excitation; modal parameters identifi cation; ship structure; operational modal analysis

U661.4

A

1001-9855（2014）05-0001-16

国家自然基金资助“基于运行模态识别的舰船加筋结构动力优化方法及实验研究（51079027）”。

2014-08-18

洪 明（1959-），男，教授，研究方向：结构失效、振动和噪声机理、预报及控制研究。

雷 川（1990-），男，硕士，研究方向：结构分析及模态参数识别。

崔洪宇（1977-），男，讲师，研究方向：结构振动控制及故障诊断。