轿车轮毂轴承疲劳寿命的计算与分析

董 晓，陈东照，邓四二，牛荣军，胡广存

(1.河南科技大学机电工程学院，河南洛阳471003;2.河南机电职业学院汽车工程系，河南郑州451191)

0 引言

双列角接触球轴承与周边部件集成为轮毂轴承单元，广泛应用于各类轿车中。轮毂轴承的主要作用是承受汽车重量并为轮毂的转动提供精确引导。作为汽车的关键零部件之一，轮毂轴承的寿命直接关系到汽车的安全性与可靠性，因此，轮毂轴承寿命计算与分析是轮毂轴承设计开发过程中的一项重要工作。轮毂轴承疲劳寿命计算是在轮毂轴承载荷谱分析和轮胎载荷计算的基础上进行的。文献[1］设计了城市道路轿车轮毂轴承载荷谱测试系统，实车测试并分析了轮毂轴承的载荷特性。文献[2］研究了轮毂轴承耐久性试验载荷谱，设计了与轮毂轴承实际工作中受载较为一致的试验载荷谱。文献[3］推导了轮毂轴承的轮胎载荷计算公式，并对轮胎载荷特性进行了分析。目前，轮毂轴承寿命计算[4-6］多采用简化算法并将一套双列轴承当作两套单列轴承计算，结果与实际有一定的差别。

鉴于此，本文在滚动轴承动力学分析[7-10］基础上，建立了双列角接触球轴承内部元件间相互作用力数学模型。根据双列轴承寿命计算法，建立轿车轮毂轴承寿命计算模型。基于Fortran编程软件及Adams动力学仿真软件开发轿车轮毂轴承动力学仿真软件，分析轴向预紧量和轮毂偏移量对轮毂轴承寿命的影响。

1 轴承元件间相互作用力数学模型

轮毂轴承内部元件的受力以及运动情况非常复杂，为了对轴承进行动力学仿真，需要对其模型进行一定的简化，为此采用以下假设:(1)外圈与轴承座刚性联接，固定不动。两内圈通过一锁扣联结在一起以转速n绕X轴旋转，具有5个自由度，可承受径向载荷、轴向载荷及力矩载荷的作用。球与保持架可在任意方向转动和平动;(2)套圈、钢球保持架为刚性元件，仅在接触部位产生变形，且符合赫兹接触理论。

本文研究适用于目前各代轮毂轴承寿命计算，以用于轿车前驱动轮的一代轮毂轴承为例，其受载示意图如图1所示。轴承元件间的相互作用力分析是轴承寿命计算的基础。在考虑赫兹接触、润滑与摩擦的基础上，建立了双列角接触球轴承内部元件间的相互作用力数学模型。轮毂轴承内部元件间的相互作用力主要有钢球与滚道间的法向接触力与油膜拖动力，钢球与保持架兜孔间的接触力与油膜力等。

1.1 钢球与滚道的接触载荷

由经典赫兹接触理论可知，第j个钢球与滚道接触时所产生的接触力为:

式中，下标i、o分别表示内、外滚道(下同);Ki(o)j为第j个钢球与滚道接触处的负荷-变形常量，求解表达式见文献[10］;δi(o)j为第j个钢球与滚道间的弹性变形量，可由滚道沟曲率中心相对于钢球中心的距离gi(o)j确定。

图2为滚道沟曲率中心相对于钢球中心的距离gi(o)j示意图。图2中省略了钢球序号j。Ob、Oi、Oo分别代表位移后的钢球中心、内沟曲率中心和外沟曲率中心。xi(o)、yi(o)分别为钢球中心相对于沟曲率中心在坐标轴xb、yb方向的距离，可通过Adams系统函数测得。由图2可知:第j个钢球与滚道间的弹性变形量δi(o)j及接触角αi(o)j可表示为:

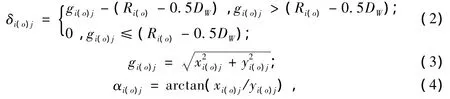
式中，Ri(o)为沟曲率半径;DW为钢球直径;αi(o)j为钢球与滚道间的接触角。

图1 轿车轮毂轴承受载示意图

1.2 钢球与滚道间的拖动力

考虑轴承的润滑状态为边界润滑、混合润滑以及流体动压润滑，钢球与滚道接触面之间润滑剂的拖动力为:

式中，μi(o)j为润滑剂的拖动系数，由润滑剂特性及润滑状态决定，具体计算方法见文献[11］。

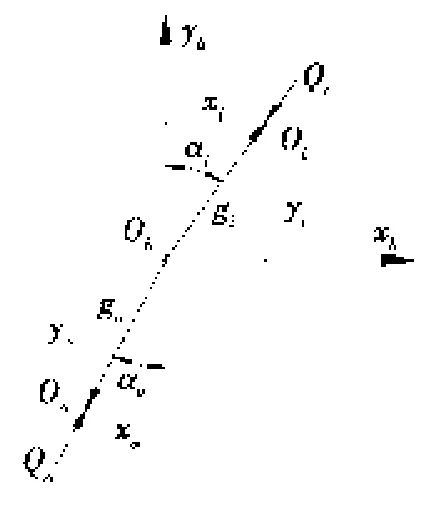
图2 gi(o)j示意图

1.3 钢球与保持架之间的作用力

在SHABERTH第5代角接触球轴承实验模型基础上引入钢球与保持架之间发生弹性变形量，则钢球与保持架兜孔间的法向作用力Qcj为:

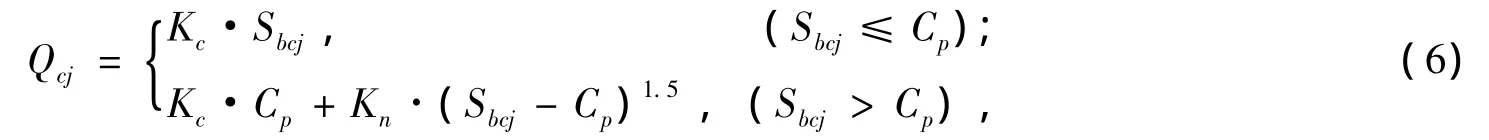
式中，Kc为试验数据确定的线形逼近常量，对于球轴承可取Kc=11/Cp;Cp为保持架兜孔间隙，Cp=0.5×(Dp-DW)，Dp为保持架兜孔直径;Kn为钢球与保持架兜孔接触处的负荷-变形常量，具体计算方法见文献[10］;Sbcj为钢球中心相对于兜孔中心的位移，可通过Adams系统函数测得。

2 轿车轮毂轴承寿命计算模型

2.1 滚动轴承疲劳寿命

文献[10］介绍了滚动轴承疲劳寿命的计算方法，计算公式为:

式中，点接触 e=10/9，线接触 e=9/8;L10，1、L10，2、…、L10，k分别为轴承中各个套圈的额定寿命，k 为一套轴承中套圈的个数，每个套圈的额定寿命计算公式为:

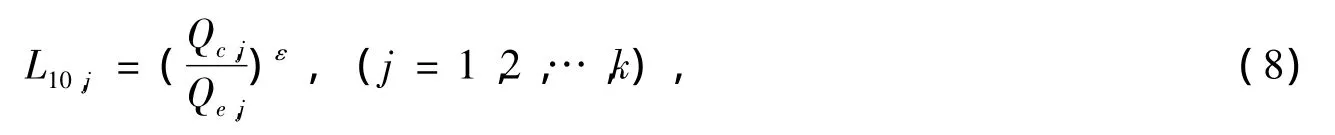
式中，Qc为套圈的额定滚动体负荷;Qe为套圈的当量滚动体负荷;点接触ε=3，线接触ε=4。

额定滚动体负荷Qc可由下式求得:

点接触:

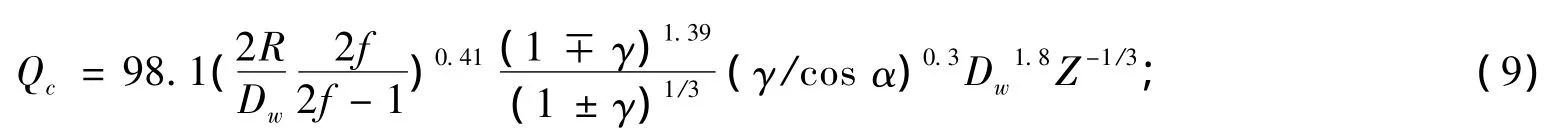
线接触:

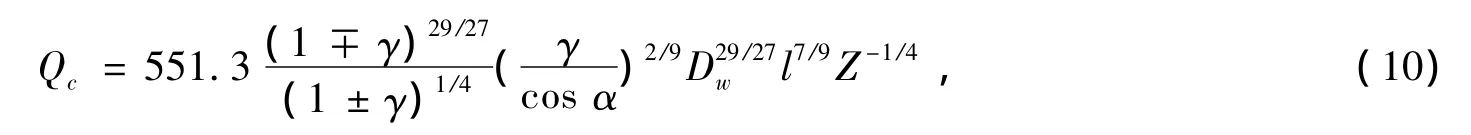
式中，上面符号适用于内圈，下面符号适用于外圈;f为沟曲率半径系数;Dw为滚动体直径;R为滚动体母线曲率半径;Z为单列钢球数;γ为无量纲几何参数，γ=(Dwcos α)/dm。

若套圈相对于负荷方向旋转，其当量滚动体负荷为:

若套圈相对于负荷方向静止，其当量滚动体负荷为:

式中，点接触时，s=3，w=10/3;线接触时，s=4，w=9/2;Qj为钢球与滚道间的法向接触力，可由式(1)求得。

若套圈有i列滚道，且各列的额定滚动体负荷均为Qc，每列的当量动负荷为Qe，p(p=1，2，…，i)，套圈总的额定动负荷为 Q'c，总的当量动负荷为 Q'e，则 Q'c与 Qc，Q'e与 Qe，p之间有如下关系[12］:

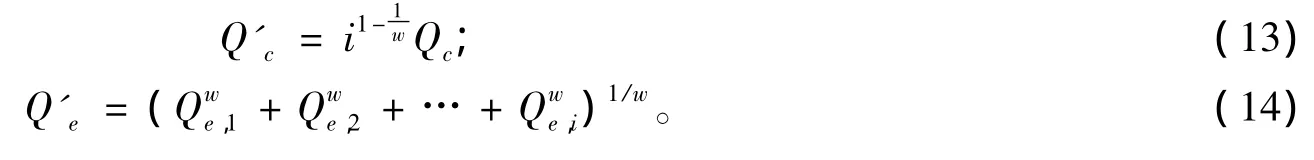
2.2 轿车轮毂轴承疲劳寿命

轿车轮毂轴承作为滚动轴承的一种特殊形式，其寿命计算既具有滚动轴承寿命计算的普遍性，又需要考虑轮毂轴承应用的特殊性。轿车轮毂轴承载荷谱制定和轮胎载荷计算是寿命计算的基础。

本文参照NTN(恩梯恩)公司制定的侧向加速度使用率和车速取值方法。侧向加速度ag、使用率q及载荷冲击因数fw见表1。直线较好路面行驶车速取100 km/h，直线较差路面行驶车速取60 km/h，保持右转弯或左转弯时车速取40 km/h。每组行驶状态下主轴的转速为:

式中，v为实际车速;Rs为轮胎有效半径。

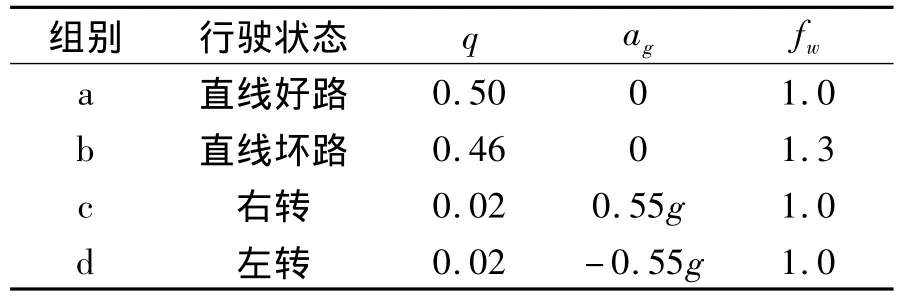
表1 侧向加速度使用率及载荷冲击因数

由文献[3］可知，轿车的轮胎载荷为:

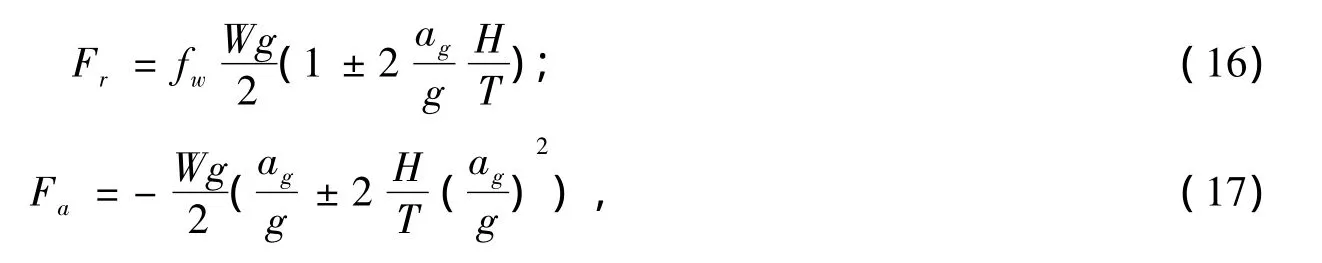
式中，Fr、Fa分别为径向轮胎载荷和轴向轮胎载荷;“+”适用于左侧车轮，“-”适用于右侧车轮;g为重力加速度，g=9.81 m/s2。

轮毂用双列角接触球轴承的寿命由轴承的3个套圈(即2个内圈和1个外圈)的寿命综合决定。将轿车相关参数与侧向加速度代入式(16)和式(17)，可得到每种行驶状态下的轮胎载荷Fr与Fa，然后将轴承结构参数和工况参数Fr、Fa和n输入轿车轮毂轴承动力学仿真软件并进行仿真计算，得到各套圈的额定滚动体负荷 Qc和当量滚动体负荷 Qe，t(t=a，b，c，d)。

由于不同行驶状态下的轮胎载荷和转速不同，为计算轴承寿命，应按寿命相等的原则，将转速转化为平均转速，当量滚动体负荷转化为平均当量滚动体负荷，再计算轴承寿命。平均转速nm及平均当量滚动体负荷Qem可通过下列公式[10］计算:

将求得的各套圈的额定滚动体负荷Qc和平均当量滚动体负荷Qem代入式(8)，求得2个内圈和1个外圈的寿命分别为L10i1、L10i2、L10o，下标1和下标2分别表示轴承外列、轴承内列。

将求得的各套圈寿命代入式(7)，得到轮毂用双列角接触球轴承的寿命为:

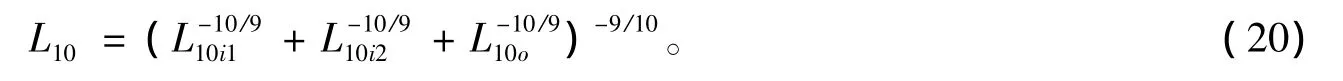
一般用车辆行驶里程表示轴承的寿命[13］:

式中，Lk为以公里数表示的轮毂轴承寿命;L10为以百万转表示的轮毂轴承寿命。

3 计算结果与分析

本文在滚动轴承动力学分析基础上，建立轿车轮毂轴承内部元件间相互作用力的数学模型，联合Adams动力学仿真软件与Fortran编程软件开发轿车轮毂轴承动力学仿真软件。以某前轮驱动轿车的前轴右轮轮毂轴承为例，分析轴向预紧量与轮毂偏移量对轴承寿命的影响。轿车相关参数:前轴质量W=935 kg，质心高度H为480 mm，轮距T为1 565 mm，轮毂偏移量(外侧为“+”，内侧为“-”)e为-3 mm，轮胎有效半径Rs为292 mm。轮毂轴承主参数:轴承外径为80 mm，内径为42 mm，宽度为45 mm，钢球直径为12.7 mm，每列有13个钢球，初始接触角为35°，保持架由钢球引导。

将车速、轿车及轮毂轴承相关参数代入式(15)～式(17)，可得到如表2所示载荷谱。

3.1 轴向预紧量对轮毂轴承寿命的影响

轮毂轴承的轴向预紧量对轮毂轴承受力和内部载荷分布具有显著影响。为使轴承的使用性能得到充分保证，需对其进行轴向定位预紧。

轮毂轴承寿命与轴向单侧预紧量的关系如图3所示。由图3可知:随着轴向预紧量的增大，轴承寿命呈现先增大后减小的趋势。轴向预紧量的增大使轴承受载钢球增多，受载更加均匀。图4为各套圈平均当量滚动体负荷随轴向预紧量变化曲线。由图4可知:在轴向预紧量由0 μm增大到27 μm过程中，外列内圈的平均当量滚动体负荷变化不大，内列内圈和轴承外圈的平均当量滚动体负荷减小;当轴向预紧量由27 μm继续增大，各套圈的平均当量滚动体负荷均急剧增大。套圈额定滚动体负荷不变，故轴承寿命随轴向预紧量的增大呈现先增大后减小的趋势。存在一个最佳轴向预紧量使轮毂轴承的寿命最大，对于本文所研究的轴承，当轴向预紧量取27 μm时，轴承获得最大寿命4.5×105km。

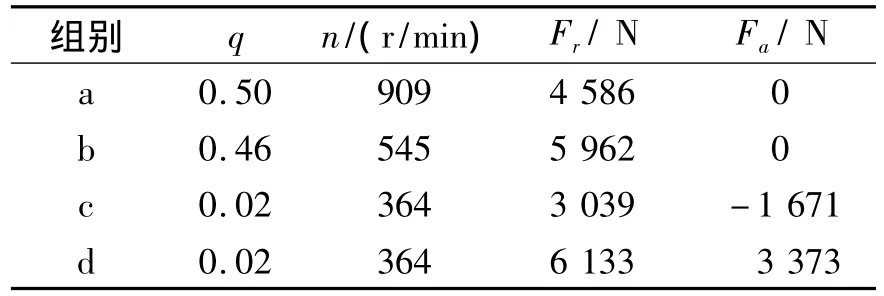
表2 载荷谱

3.2 轮毂偏移量

在单侧预紧量为27 μm的条件下，分析轮毂偏移量对轴承寿命的影响。轴承寿命与轮毂偏移量的关系如图5所示。由图5可知:在轮毂偏移量由-10 mm变化到10 mm过程中，轴承寿命先增大后减小，偏移量为3 mm时，轴承寿命取得最大值4.74×105km。轮毂偏移量改变引起轮胎载荷对轮毂轴承中心产生的力矩载荷的变化，影响轴承内部载荷分布。图6为各套圈平均当量滚动体负荷随轮毂偏移量变化曲线。由图6可知:在轮毂偏移量由-10 mm变化到3 mm过程中，外列内圈的平均当量滚动体负荷变化不大，内列内圈和轴承外圈的平均当量滚动体负荷急剧减小，故此时轴承寿命增大;在轮毂偏移量由3 mm变化到10 mm过程中，外列内圈和内列内圈的平均当量滚动体负荷增大，轴承外圈平均当量滚动体负荷减小，此时轴承寿命减小。因此，为使轴承寿命最大，应合理确定轮毂偏移量。

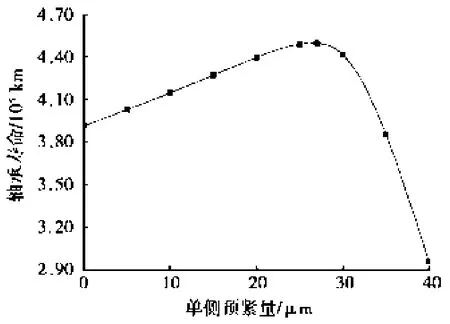
图3 轴承寿命与轴向预紧量的关系

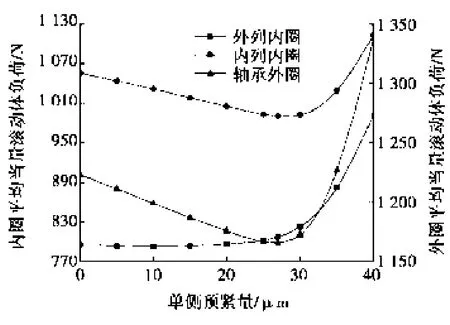
图4 平均当量滚动体负荷与轴向预紧量的关系

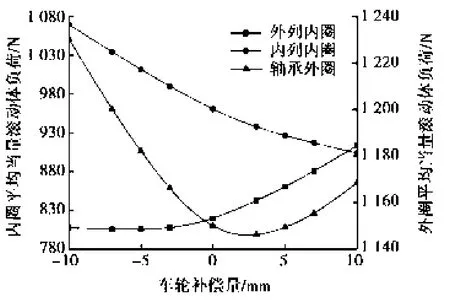
图6 平均当量滚动体负荷与轮毂偏移量的关系

4 结束语

在双列角接触球轴承动力学分析的基础上，建立轿车轮毂轴承疲劳寿命计算模型，分析了轴向预紧量和轮毂偏移量对轮毂轴承寿命的影响，得出轴承轴向预紧量和轮毂偏移量对轿车轮毂轴承寿命影响显著，为使轴承寿命达到最大，应合理确定预紧量和轮毂偏移量。

[1]张雪萍，陈以农，姚振强.轿车轮毂轴承城市道路载荷谱测试与分析[J］.上海交通大学学报，2001，35(12):1813-1816.

[2]盛英英，黄德杰，尹迪江，等.轿车轮毂轴承耐久性试验载荷谱的研究[J］.机电工程，2010，27(6):40-51.

[3]黎桂华，黄平，赵联春，等.轿车轮毂轴承外部载荷计算方法及其特性[J］.润滑与密封，2006，183(11):17-20.

[4]李兴林.中国轿车轮毂轴承寿命研究[D］.上海:上海交通大学，1999.

[5]黎桂华.轿车轮毂轴承寿命计算及其耐久性试验研究[D］.广州:华南理工大学，2004.

[6]傅强，黄德杰，游红武，等.轿车轮毂轴承寿命的估算[J］.新技术新工艺，2011(5):16-19.

[7]Harris T A.Rolling Bearing Analysis[M］.5 ed.New York:John Wiley ＆ Sons Inc，2006.

[8]Walter C T.The Dynamic of Ball Bearings[J］.ASME JLT，1970(1):39-53.

[9]Gupta P K.Advanced Dynamics of Rolling Elements[M］.New York:Springer-Verlag，1984.

[10]邓四二，贾群义.滚动轴承设计原理[M］.北京:中国标准出版社，2008.

[11]梁国利，段明德，赵海莲，等.轴承刚度对主轴-卡盘-工件系统动态特性的影响[J］.河南科技大学学报:自然科学版，2013，34(4):21-25.

[12]余俊.滚动轴承计算:额定负荷、当量负荷及寿命[M］.北京:高等教育出版社，1993.

[13]陈以农.城市用轿车轮毂轴承载荷测试与分析[D］.上海:上海交通大学，2001.