基态Bn（n=2，3）结构与完全解析势能函数

祝恒江，路俊哲，魏 婕，刘立仁

（新疆师范大学物理与电子工程学院，乌鲁木齐830054）

1 引 言

硼块体材料呈现半导体性质，具有低密度、高熔点、高ΔH燃烧及金刚石般的硬度，无论是从体积和重量的标准看，它都是一种高能材料，是一种令人特别感兴趣的火箭推进剂.硼可以和其他元素合成为很多有用的金属及无机化合物的富硼材料（以硼为基础含有少量其它元素，但性质有重大改变的材料），它们一般都很硬，熔点高，导电、导热性好，具有广泛的应用前景.如爆炸，材料精炼与提纯，高弹纤维混合物，化学性质稳定的绝缘体，高温半导体设备和热电转换材料等方面都要涉及到硼和富硼材料.因此，硼被视为是元素周期表中最令人感兴趣的化学元素之一.

多年以来，硼材料的实验和理论研究都十分活跃，主要集中在硼纳米材料、硼超导材料、硼表面活性研究及硼的电学性质等方面.实验方面，人们已经通过分子束外延技术和激光烧蚀技术合成了硼团簇，并通过飞行时间质谱技术研究了它的性质，预言纯硼团簇是三维结构［1］.理论方面的报道也很多，其中Boustani［2］采用从头计算方法研究了小硼团簇Bn（n=2～14）的几何和电子结构，预言n＞9时，硼团簇的最终结构主要由六边锥或五边锥组成，以准平面或凸起结构作为空心球或纳米管的表面部分.Lau［3-4］等报道了B12和B24的几何结构与振动性质，指出B12的基态结构是凸平面，B24的基态结构为双环结构.LI［5-7］等报道了B8，B7和B5的结构和稳定性，指出它们的基态构型分别是硼原子位于中心的七边形，六边锥和平面五边环结构.刘立仁［8］等人利用密度泛函理论方法计算并分析了Bn（n=2～15）团簇的几何结构和电子性质.另外，对B6，B4，B3和B2的结构和稳定性也都有相关报道［9-11］.

大部分富硼材料的结构多是基于一种刚性的三维网状结构，具有低密度、高硬度和高的化学稳定性.近几年，富硼材料的实验和理论研究主要集中在三元硼化物，氮化硼，碳化硼和富硼氧化物.三元硼化物AlMgB14材料具有高硬度，高韧性，低密度，低摩擦系数以及抗高温氧化腐蚀等众多优异性能，在工具、模具、微机械制造及航空航天关键零部件等领域具有重要的应用前景［12-15］.氮化硼化合物因其在核技术，半导体和钢铁工业等领域的广泛应用而倍受关注［16］.碳化硼具有超常的硬度及较高的中子吸收能力，高熔点，高抗弯强度，高弹性模量等特点，具有耐酸碱，抗氧化，不易侵蚀等优良十分的化学性质，被广泛应用于工程陶瓷、核工业和航空航天等领域［17］.富硼氧化物因具有低密度，高硬度，高机械强度，高熔点，高化学稳定性，高热导率等特殊性质可望成为有发展前景的新型的工业超硬材料［18-20］.

分子势能函数一直是理论化学、原子分子物理等学科的重要研究课题之一，对分析研究分子的结构和性质都非常重要，同时也是研究分子形成和离解的重要基础，通过势能函数也可进行反应动力学计算，可对分子材料的制备和应用提供理论指导，其重要作用体现在：（1）分子本身几何结构及电子的完整描述；（2）构造多原子分子全空间势能函数的基础；（3）研究分子稳定性的依据；（4）研究原子与分子碰撞和分子反应动力学的基础.

硼和富硼材料的理论和实验研究都十分活跃，但B2，B3分子及其离子的势能函数研究十分有限，这与硼的化学元素地位甚不相称.据作者所知，目前仅有闫安英［21］等人利用密度泛函理论B3LYP方法给出了B2基态分子结构及势能函数及杨传路，朱正和［25］等人利用从头计算QCISD方法给出了B3分子的结构和势能函数的文献报道.文献［21］所用方法比较粗略，相应得出的数据与实验数据有较大误差，而文献［25］在确定多体项展式势能函数三体项线性系数和非线性系数时，没有考虑它们之间的关联，所得解析势能函数不能准确再现B3分子基态平衡结构的全部特征，未能实现用一个势能函数同时描述多个极小点的性质或由一种稳定构型的数据确定其它稳定构型的势能面.鉴于此，B2及B3分子及其离子的势能函数值得进一步进行理论与实验研究.本文使用Gaussian03程序包，采用单双取代耦合簇（CCSD）方法，选择基组6-311+g（2df），对B2分子的基态进行优化计算，采用十一参量Murrell-Sorbie函数，运用最小二乘法拟合得到B2分子基态解析势能函数，给出与实验值符合很好的光谱常数.使用同样的方法和基组，对B3分子的基态结构进行优化计算，采用多体项展式法，考虑线性系数和非线性系数之间的关联，得到B3分子基态完全解析势能函数.势能面静态特征表明，该势能函数准确再现了B3分子基态全部平衡结构特征.

2 理论计算

2.1 B2基态分子结构及势能函数

关于双原子分子解析势能函数的理论研究，主要采用单点能扫描拟合方法.B2分子基态解析势能函数的确定一直是个难题，相关研究少有报道.文献［21］利用密度泛函理论B3LYP方法，选用不同的基组对B2分子进行优化得到其基态稳定构型，选用最优组合DFT-B3LYP／cc-PVTZ对B2分子基态进行单点能扫描，采用五参数Murrell-Sorbie函数进行非线性最小二乘法拟合，得到了B2分子基态解析势能函数.文献［22］利用已有的光谱常数数据，经零点能校正，推算出B2分子基态五参数Murrell-Sorbie解析势能函数.

B2分子是一个简单体系，但事实表明对B2分子解析势能函数的理论研究却相当困难.原因在于，理论计算时，同一方法不同的基组，甚至不同的初始猜，都会使计算结果有较大差异.对采用单点能扫描拟合方法得到双原子分子势能函数而言，选取一个合理的势能函数关系十分重要，且单点能的扫描方式和初始猜的确定也非常关键.Murrell-Sorbie函数能准确反应基态双原子分子的排斥支和吸引支，正确反应其离解极限和长程势，是用于描述双原子分子势能函数的最佳选择.为提高势能函数的精度，采用十一参量Murrell-Sorbie函数，其形式为：

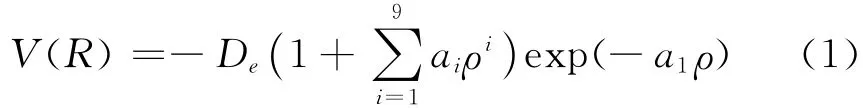
式中ρ=R-Re，R 为核间距，Re为平衡间距，离解能De及a1-a9为Murrell-Sorbie函数参数.为了确定（1）式，需确定Re、De、a1-a9.首先，采用单双取代耦合簇（CCSD）方法，参考Re，De，谐振频率ωe及电子态的实验数据及已有的理论计算结果，选用不同基组对B2分子进行优化计算，确定最优基组为6-311+g（2df），计算得到相应数据和结果列表1.然后，采用CCSD 方法，选择6-311+g（2df）基组，对B2分子进行单点能扫描，将得到的一系列单点势能值采用最小二乘法进行拟合，得到Murrell-Sorbie函数参数De和a1-a9列表2.

图1给出B2分子的基态势能曲线，从中可以看出：在计算范围内单点能扫描得到的能量点与拟合曲线完全重合（其中实线为拟合结果，圆圈为单点能扫描结果）.由（1）式可得拟合参数与力常数的关系：

其中力常数f2、f3、f4与光谱常数的关系为：

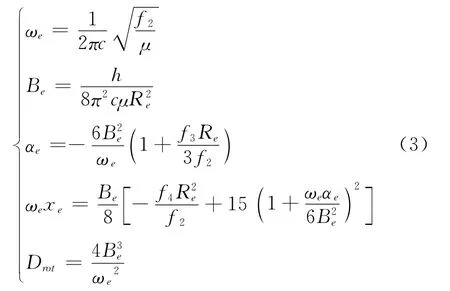
其中μ为单个原子的约化质量，ωe为谐振频率，xe为非谐振动因子，c为真空光速，Be和αe为刚性和非刚性转动因子，Drot为离心畸变常数.由（2）、（3）两式和表2，得到与实验值符合很好的B2分子光谱常数列于表3.说明拟合得到的势能函数能够正确描述B2分子基态势能函数性质.

表1 B2分子的平衡间距、离解能、谐振频率与电子态Table 1 The optimized structural parameters for B2

从表1、表2 和表3 可知，与实验值相比较，本文所得结果与实验值符合很好，且相应数值均好于文献值.另外，与优化计算值相比，拟合得到的De和ωe与实验值符合的更好.

表2 B2分子离解能、Murrell-Sorbie函数参数Table 2 The dissociation energy and M-S potential energy function parameters for B2

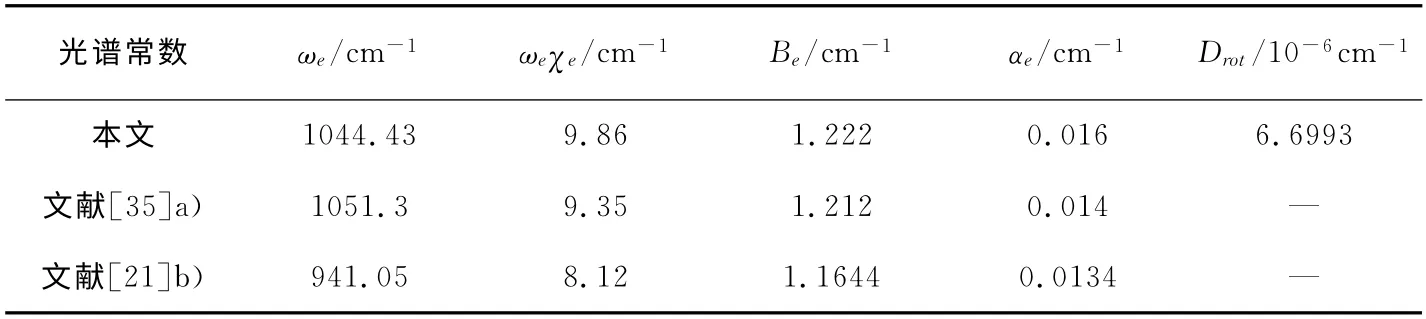
表3 B2分子的光谱常数Table 3 The spectroscopic constants for B2

表4 B3分子基态线型、角型构型参数和离解能Table 4 The structure parameters and the dissociation energies of line-and angle-type

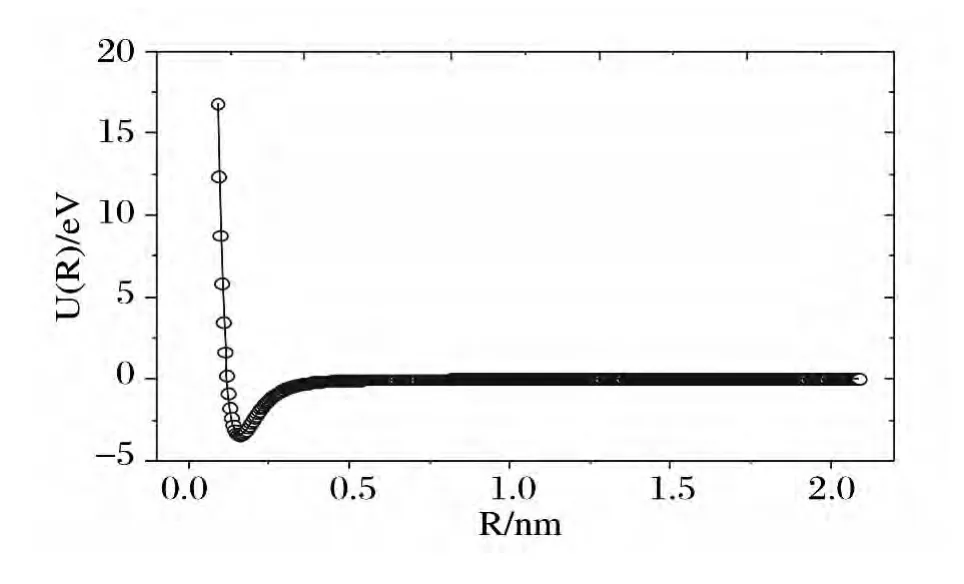
图1 B2分子的势能曲线Fig.1 The potential energy curve of B2

2.2 B3分子的平衡结构及力学常数

B3分子与B2分子的情况不同，B2分子仅有D∞h一种稳定构型，其电子态为X3∑-g.而B3分子则可能有C2v，C∞v，D∞h，D3h等四种稳定构型.本文采用CCSD 方法，选择6-311+g（2df）基组，优化计算B3分子二重态，得到C2v，C∞v，D∞h，D3h四种稳定构型，其基态平衡构型为D3h，电子态为2A′1.B3分子四种稳定构型的结构参数和离解能列于表4，C2v构型的振动频率与力常数列于表5.

表6给出了B3分子基态平衡构型及相应的电子态与文献结果的对比.由表6可知，本文优化计算得到了B3分子基态全部可能的平衡构型.这与文献［2，8，25］既相同又有较大区别，文献［25］仅优化得到D∞h（2Πu），D3h（2A′1）两种平衡构型，而文献［2］和文献［8］则只分别优化得到C2v（2A1），D3h（2A′1）两种平衡构型及C2v（2A′），D∞h（2∑），D3h（2A′）三种平衡构型.

表5 B3分子C2v构型振动频率与力常数Table 5 The structure parameters of ground state and the force constants for B3

表6 B3分子基态平衡构型（电子态）与文献结果比较Table 6 Equihbrium geometry and electronic State of B3compared with literature

2.3 基态B3分子的离解极限

在多原子分子势能函数的研究中，正确的离解极限是必不可少的.因为在表述原子，分子及其离子的势能函数中，必须知道在分子离解极限中各原子和原子团的电子状态，才能给出多体展式中各级展式的解析势能函数，从而得出多原子分子的势能函数表达式.与双原子的情况一样，要确定多原子分子正确的离解极限，首先要确定电子态，利用从头计算结合电子组态法的分析可以确定电子态，由分子反应静力学原理可确定分子可能的电子态和离解极限.对于D3h构型的分子，其离解极限的确定比较特殊，需经C2v构型变形并结合微观过程的可逆性原理才能确定可能的电子态，从而确定离解极限［25］.计算结果表明B3分子的基态平衡构型为D3h，电子态为2A′1.因此B3分子可按分离原子法指出的方式离解，又2Pu为B原子的基电子态，X3∑-g为B2分子的基电子态，符合能量最优原理，结合原子分子反应静力学中的微观过程传递性原理和B2（X3∑-g）分子的离解极限，故确定B3分子的离解极限为：

2.4 B3分子基态完全解析势能函数

根据多体项展式理论，如果设基态原子的能量为零，则基态B3分子的多体项展式势能函数可写为：

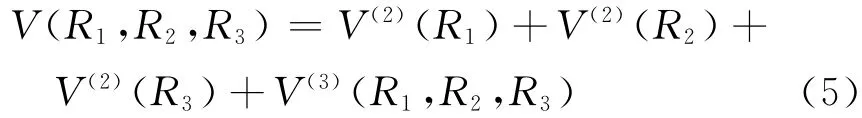
（5）式中R1=R12，R2=R23，R3=R31；V（2）（Ri）（i=1，2，3）为两体项，可由（1）式得到；V（3）（Ri）（i=1，2，3）为三体项，其形式为：

其中P 为多项式，T 为量程函数，分别为：

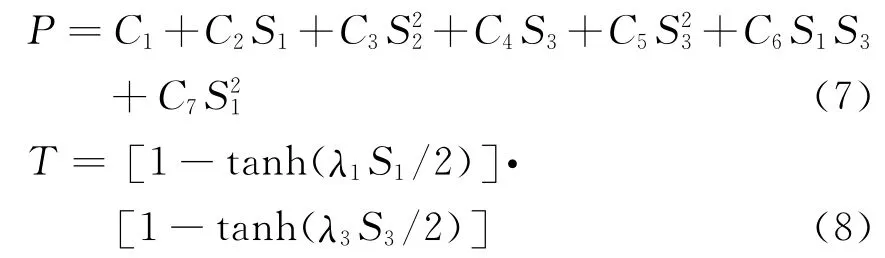
B3分子的基态构型为D3h.为简化多体项形式，（6）、（7）两式是以C2v构型为参考构型，并采用对称内坐Si（i=1，2，3），内坐标ρi向对称性坐标变换如下：

其中内坐标ρi=Ri-R0i（i=1，2，3），优化内坐标中的S2对R1和R2的交换是反对称的，但R1和R2交换之后分子结构是等同的，为了满足这一物理性质，（6）式中S2只能含有偶次项.（6）、（7）两式中含有7个线性系数Ci（i=1，2，3，4，5，6，7）和两个非线性系数λ1、λ3.利用B3分子平衡态C2v的几何结构参数、力常数和离解能，以及Ci（i=1，2，3，4，5，6，7）与λ1、λ3的函数关系，对B3分子势能面进行非线性优化得到λ1、λ3，进而得到7个线性系数Ci（i=1，2，3，4，5，6，7），结果列于表7.

为了直观分析势能函数特性，展示对称性与分子结构以及分子的形成与离解的机理，根据已得出的数据参数，由（4）式图绘出B3分子的伸缩振动和旋转等值势能图2～图6，正确复现了B3分子的稳态能量和平衡结构.

表7 B3分子势能函数三体项参数Table 7 Coefficients of 3-body term of potential energy function for B3

图2 是固定θ123=61.65895°时，改变键长R12，R23的B3分子势能函数的伸缩振动等值势能图.图2表明在R12=R23=0.15367nm 处有一个极小值7.564eV，准确再现了B3分子具有稳定的C2v结构特征，这与优化计算结果完全一致.与文献［25］不同，图2表明反应B+B2→B3不存在鞍点，是容易进行的无阈能反应.

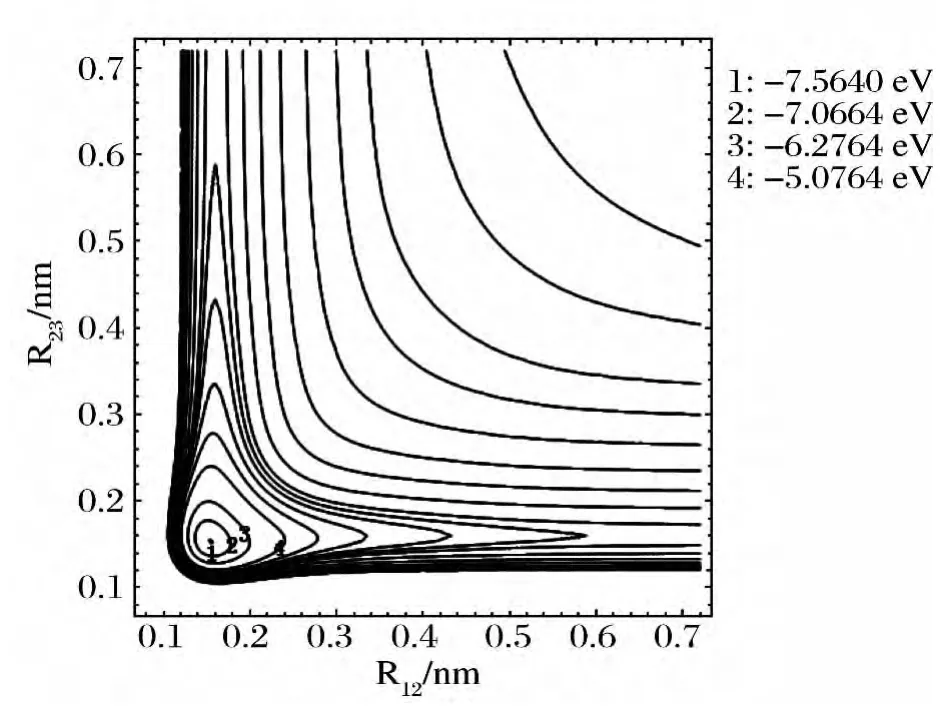
图2 B3分子的伸缩振动等值势能图 Fig.2 Stretched vibrational contour of potential energy for B3

图3 B绕B-B旋转的等值势能图 Fig.3 Rotational contour of potential energy function for Bround B-B

图3将R12=0.15367nm 固定在X 轴上，以R12键的中点为原点建立Y 轴，另一B 原子绕R12键旋转时形成的等值势能图.从图3可以看出，当另一B原子旋转到θ123=61.65895°，θ231=θ312=59.17053°处，有一个极小值7.5645eV，准确再现了B3分子稳定的C2v构型；当另一B 原子旋转到θ123=θ231=θ312=60°处，有一个极小值7.5501 eV，准确再现了B3分子稳定的D3h构型；当另一B原子旋转到θ321=180°处，有一个极小值6.18 eV，表明B3分子具有一个稳定的C∞v构型；当另一B 原子旋转到θ213=180°处，有一个极小值7.07492eV，表明B3分子具有一个稳定的D∞h构型.由此可知基态B3分子具有C2v，D3h，C∞v和D∞h四个稳态构型.图4是图3的局部放大.

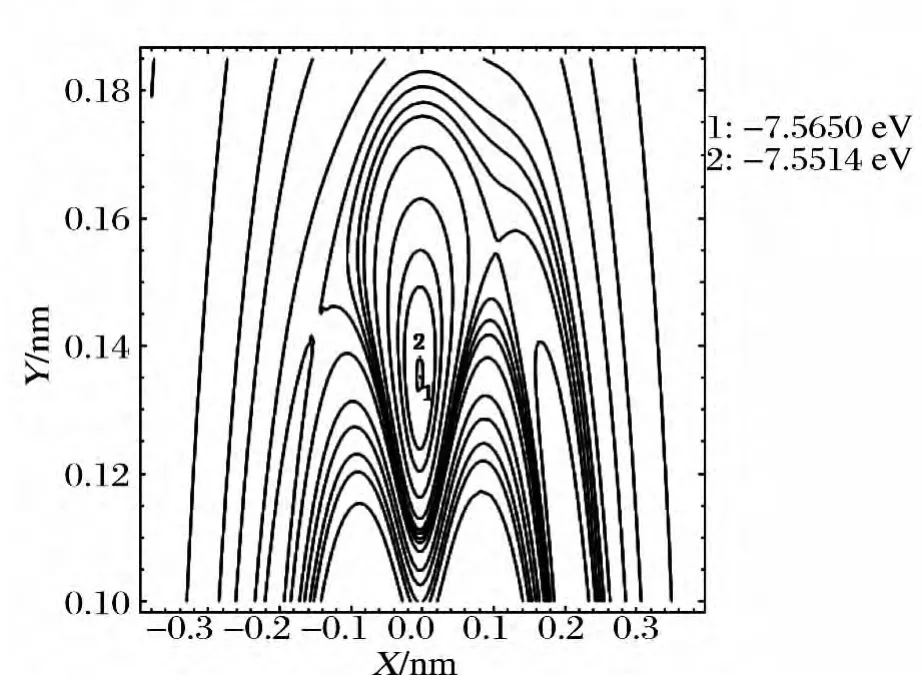
图4 B绕B-B旋转的等值势能图 Fig.4 Rotational contour of potential energy function for Bround B-B

图5 B绕B-B旋转的等值势能图Fig.5 Rotational contour of potential energy function for Bround B-B

图5将R13=0.15751nm 固定在X 轴上，以R13键的中点为原点建立Y 轴，另一B 原子绕R13键旋转时形成的等值势能图.图5同样表明在θ123=61.65895°，θ231=θ312=59.17053°处，有一个极小值7.5645eV，准确再现了B3分子稳定的C2v构

型；当另一B 原子旋转到θ123=θ231=θ312=60°处，有一个极小值7.5491eV，准确再现了B3分子稳定的D3h构型；当另一B原子旋转到θ213=θ132=180°处，有两个相同的极小值7.0628eV，准确再现了B3分子稳定的D∞h构型.图6是对图5的局部放大.

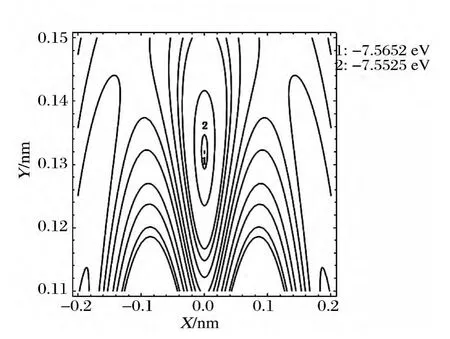
图6 B绕B-B旋转的等值势能图Fig.6 Rotational contour of potential energy function for Bround B-B

图2～图6表明，本文所得B3分子基态解析势能函数准确再现了B3分子基态全部平衡结构特征，与优化计算结果完全一致，是B3分子基态的完全解析势能函数，实现了用一个势能函数同时描述多个极小点的性质或由一种稳定构型的数据确定其它稳定构型的势能面.这正是多体项展式理论的特有优点，而从头计算和LEPS 函数等方法则是不可能的.

3 结 论

本文使用Gaussian03程序包，采用单双取代耦合簇（CCSD）方法，选择基组6-311+g（2df），对B2分子的基态进行优化计算，采用十一参量Murrell-Sorbie函数，运用最小二乘法拟合得到B2分子势能函数，得到与实验值符合很好的光谱常数；对B3分子的基态平衡结构进行优化计算，采用多体项展式法，利用B3分子平衡结构C2v的几何参数、力常数和离解能，以及线性系数Ci（i=1，2，3，4，5，6，7）与非线性系数λ1、λ3的函数关系，先在极小点附近对B3分子势能面进行非线性优化拟合得到λ1、λ3，进而得到Ci，得到基态B3分子的完全解析势能函数，准确再现了B3分子基态全部平衡结构特征，实现了用一个势能函数同时描述多个极小点的性质或由一种稳定构型的数据确定其它稳定构型的势能面.

［1］ Hanley L，Whitten J L，Anderson S L.Collision-in-duced dissociation and initio studies of boron cluster ions：determination of structures and stabilities［J］.J.Phys.Chem.，1988，92（20）：5803.

［2］ Boustani I.Systematic ab initio investigation of bare boron clusters：determination of the geometry and electronic structures of Bn（n=2～14）［J］.Phys.Rev.B，1997，55（24）：16426.

［3］ Lau K C，Deshpande M，Pandey R.A theoretical study of vibrational properties of neutral and cationic B12clusters［J］.Int.J.Quantum Chem.，2005，102（05）：656.

［4］ Lau K C，Deshpande M，Pati R，et al.A theoretical study of electronic and vibrational properties of neutral，cationic，anionic B24clusters［J］.Int.J.Quantum Chem.，2005，103（06）：866.

［5］ Li Q S，Zhao Y，Xu W G，et al.Structure and stability of B8clusters［J］.Int.J.Quantum Chem.，2005，101（02）：219.

［6］ Li Q S，Gong L F，Gao Z M.Structures and stabilities of B7，B7+and B7-clusters［J］.Chem.Phys.Lett.，2004，390（01）：220.

［7］ Li Q S，Jin H W.Structure and stability of B5，B5+and B5-clusters［J］.J.Phys.Chem.A，2002，106（30）：7042.

［8］ Liu L R，Lei X L，Chen H，et al.Geomtry and electronic properties of Bn（n=2～15）clusters［J］.Acta Phys.Sin.，2009，58（08）：5355（in Chinese）［刘立仁，雷雪玲，陈航，等.Bn（n=2～15）团簇的几何结构和电子性质［J］.物理学报，2009，58（08）：5355］

［9］ Zhai H J，Wang L S，Alexandrova A N，et al.Photoelectron spectroscopy and ab initio study of B3-and B4-anions and their neutrals［J］.J.Phys.Chem.A，2003，107（44）：9319.

［10］ Yang C L，Zhu Z H，Wang R，et al.Analytical potential energy functions of the neutral and cationic B2［J］.J.Mol.Struct：THEOCHEM，2001，548：47.

［11］ Ma J，Li Z H，Fan K N，et al.Density functional theory study of the B6，B6-and B62-cluster［J］.Chem.Phys.Lett.，2003，372（05）：708.

［12］ Jiang X，Qu W H，Zhao J J，et al.Experimental and therotical study on the mechanical properties of AlMgB14［J］.Sci.China：Phys，Mech & Astron，2011，41（06）：764（in Chinese）［蒋雪，曲文超，赵纪军，等.AlMgB14三元超硬硼化物的实验制备与理论研究［J］.中国科学：物理学，力学，天文学，2011，41（06）：764］

［13］ Cook B A，Harringa J L，Lewis T L.A new class of ultra-hard materials based on AlMgB14［J］.Scr.Mat.，2000，42（06）：597.

［14］ Russell A M，Cook B A，Harringa J L.A theoretical of thermal expansion of AlMgB14［J］.Scr.Mat.，2002，46（09）：629.

［15］ Higashi I，Ito T.Coefficient of thermal expansion of AlMgB14［J］.J.Less.Common.Met.，1983，92（02）：239.

［16］ Xu Y，Li Q S.A quantum chemistry study：a new kind of boron nitrides［J］.J.Mol.Sci.，2006，22（06）：03（in Chinese）［徐羽，李前树.一系列新型硼氮化合物的理论研究［J］.分子科学学报，2006，22（06）：03］

［17］ Tang G H，Zhang X H，Chen C Q.A comprehensive review on boron carbide ［J］.Mater.Rev.，1994，4（04）：69（in Chinese）［唐国宏，张兴华，陈昌麒.碳化硼超硬材料综述［J］.材料导报，1994，4（04）：69］

［18］ Drummond M L，Meunier V，Sumpter B G.Structure and stability of small boron and boron oxide clusters［J］.J.Phys.Chem.A，2007，111（28）：6539.

［19］ Nguyen M T，Matus M H，Ngan V T.Thermochemistry and electronic structure of small boron and boron oxide clusters and their anions［J］.J.Phys.Chem.A，2009，113（17）：4895.

［20］ Feng X J，Luo Y H，Liang X.Theoretical study of structure and stability of BnO and BnO2clusters［J］.Journal of Cluster Science，2008，19（02）：421.

［21］ Yan A Y，Wang F N，Song X S，et al.Molecular structure and potential energy function for ground state of B2［J］.Journal of Sichuan Normal University：Natural Science，2010，33（04）：0516（in Chinese）

［22］ Zhu Z H，Yu H G.Molecular structure and potential energy function ［M］.Beijing：Science Press，1997（in Chinese）［朱正和，俞华根.分子结构与势能函数［M］.北京：科学出版社，1997］

［23］ Yang C L，Zhu Z H，Wang R，et al.Analytical potential energy function of the neutral and cationic B2［J］.J.Mol.Stru.，2001，548：47.

［24］ Xie A D，Zhu Z H.Potential energies of electronic state X3∑-gand A3∑-uof a B2molecule［J］.Chinese J.Comput.Phys.，2006，23（05）：594（in Chinese）［谢安东，朱正和.B2分子X3∑-g和A3∑-u态的势能函数［J］.计算物理，2006，23（05）：594］

［25］ Yang C L，Zhu Z H Wang R，et al.The structure and analytical potential energy function for B3（X2A1，）system［J］.J.At.Mol.Phys.，2001，18（03）：293（in Chinese）［杨传路，朱正和，汪蓉，等.B3分子的结构和势能函数［J］.原子与分子物理学报，2001，18（03）：293］［26］ Liu Y F，Li J Y，Hou Z Y，et al.Structure and analytic potential energy function for ground state of S3molecule［J］.J.At.Mol.Phys.，2006，23（02）：348（in Chinese）［刘玉芳，李俊玉，侯振雨，等.基态S3分子的结构与解析势能函数［J］.原子与分子物理学报，2006，23（02）：348］

［27］ Luo W L，Ruan W，Zhang L，et al.Analytical potential energy function for tritium water molecule T2［J］.Acta Phys.Sin.，2008，57（08）：4833（in Chinese）［罗文浪，阮文，张莉，等.氢同位素氚水T2O的解析势能函数［J］.物理学报，2008，57（08）：4833］

［28］ Chen X H，Jiang Y，Liu Y R，et al.Structure and analytic potential energy function of the molecules TiO，O2and TiO2［J］.Acta Phys.Sin.，2012，61（01）：013101（in Chinese）［谌晓洪，蒋燕，刘议蓉，等.TiO，O2和TiO2的分析势能函数及光谱研究［J］.物理学报，2012，61（01）：013101］

［29］ Ruan W，Hu Q L，Xie A D，et al.Structure and analytic potential energy function for ground state of MgB2molecule ［J］.Acta Phys.Sin.，2009，58（12）：8188（in Chinese）［阮文，胡强林，谢安东，等.基态MgB2分子的结构与解析势能函数［J］.物理学报，2009，58（12）：8188］

［30］ Han X Q，Jiang L J，Liu Y F.Structure and potential energy function of MgB and MgB2（1A1）［J］.Acta Phys.Sin.，2010，59（07）：4542（in Chinese）［韩晓琴，蒋利娟，刘玉芳.MgB 和MgB2（1A1）的结构与解析势能函数［J］.物理学报，2010，59（7）：4542］

［31］ Han X Q，Xiao X J，Liu Y F.The molecular structure and potential energy function of BCl and BCl2（2A1）［J］.J.At.Mol.Phys.，2011，28（2）：195（in Chinese）［韩晓琴，肖夏杰，刘玉芳.BCl和BCl2（2A1）的结构与势能函数［J］.原子与分子物理学报，2011，28（2）：195］

［32］ Han X Q，Xiao X J，Liu Y F.The ab initio and potential energy curve of OH，OCI and HOCI（1A′）［J］.Acta Phys.Sin.，2012，61（16）：163101（in Chinese）［韩晓琴，肖夏杰，刘玉芳.OH，OCI，HOCI（1A′）的从头算与势能曲线［J］.物理学报，2012，61（16）：163101］

［33］ Han X Q，Xiao X J，Liu Y F.Structure and poten-tial energy functionof XF2（X=B，N）molecular ground state［J］.Acta Phys.Sin.，2011，60（06）：063102（in Chinese）［韩晓琴，肖夏杰，刘玉芳.XF2（X=B，N）分子基态的结构与势能函数［J］.物理学报，2011，60（06）：063102］

［34］ Zhao J，Cheng X L，Yang X D，et al.Structure and analytic potential energy function for the ground state of SiF2molecule［J］.Acta Phys.Sin.，2009，58（08）：5280（in Chinese）［赵俊，程新路，杨向东，等.SiF2基态分子的结构与势能函数［J］.物理学报，2009，58（08）：5280］

［35］ David R.Lide.CRC Handbook of Chemistry and Physics：Spectroscopic Constants of Diatomic Molecules［M／OL］.Florida：CRC Press，2007.http：／／www.hbcpnetbase.Com.