带缘板摩擦阻尼片高压涡轮叶片的减振研究

孙莹，刘永泉，郝燕平，张峻峰

（中航工业沈阳发动机设计研究所，沈阳110015）

带缘板摩擦阻尼片高压涡轮叶片的减振研究

孙莹，刘永泉，郝燕平，张峻峰

（中航工业沈阳发动机设计研究所，沈阳110015）

利用干摩擦阻尼对构件进行减振是1种简单又有效的方法，广泛应用于航空发动机叶片上，可以有效限制叶片的振动应力水平。针对带缘板阻尼片的高压涡轮叶片，基于滞后弹簧模型，以1次谐波平衡法与动柔度法结合为基本算法，提出了1种由气动力计算激振力的方法，并对其影响参数进行研究。对该叶片进行了稳态应力响应的计算，得到使叶片振动应力最小的最优正压力，并对阻尼片质量进行了优化分析。结果表明：现有的阻尼片质量在比较合理的范围内，可以起到较好的减振效果，为提高减振效果可适当增加阻尼片质量。

高压涡轮；叶片；缘板；振动；激振力；干摩擦；阻尼；航空发动机

0 引言

缘板阻尼器是在相邻2个叶片缘板和伸根之间的空腔内放置1个质量块的阻尼减振结构。当发动机转动时，质量块在离心力的作用下对叶片缘板产生正压力。叶片振动时，质量块通过摩擦传递振动载荷，当接触面之间发生滑移时利用干摩擦消耗叶片的振动能量，降低振动应力，提高发动机叶片高周疲劳可靠性。这种阻尼结构在风扇、涡轮等结构上均已得到应用，如CFM56-3发动机的第1级风扇、RB211-524G/H发动机的低压涡轮叶片等都使用了缘板摩擦阻尼器。Lars Panning等[1-2]利用赫兹线性接触模型对圆柱和不对称缘板阻尼器进行了理论和实验研究；郝燕平[3,7]通过理论和实验结合的方法研究了缘板阻尼器各参数对振动响应的影响规律并得出了可用于工程计算的方法；漆文凯[4]、何尚文[5]建立了整体－局部统一滑动摩擦模型，考虑了摩擦接触的局部滑动问题；K-H. Koh[6]通过准静态实验和动态实验研究了缘板阻尼器摩擦面的力与相对位移的滞后曲线。

本文针对某发动机带缘板阻尼片涡轮叶片发生的断裂故障，通过平面叶栅试验数据和发动机台架动测数据计算激振力占气动力的百分比；并用这个激振力计算该叶片在不同摩擦点法向压力下的稳态应力响应，得到有效降低叶片动应力和振动能量的阻尼片最优正压力；对阻尼片质量进行优化分析，以获得增加发动机可靠性的最佳阻尼效果。

1 故障概述

某发动机高压涡轮叶片采用缘板摩擦阻尼片减振。该涡轮转子叶片材料为DZ22镍基高温合金。高压涡轮工作叶片叶身段长约占叶片总长70%，叶片承受了较高的离心拉伸载荷和温度负荷。

在试车中高压涡轮转子叶片曾发生断裂故障，断裂位置（如图1所示）在沿叶高距缘板前缘8 mm，尾缘12.5 mm处，发生故障时叶片的累计工作时间为76.5 h，失效模式为高周疲劳，源区在气膜孔与叶片内外壁交界锐角处。

该涡轮叶片伸根后端面的凹槽内安装有摩擦阻尼片，如图2所示，相邻叶片之间用伸根段侧壁上的3个凸耳支撑阻尼片。在工作中，离心力使阻尼片外移，对叶片起到较强的抗振阻尼作用。

图1 高压涡轮转子断裂位置

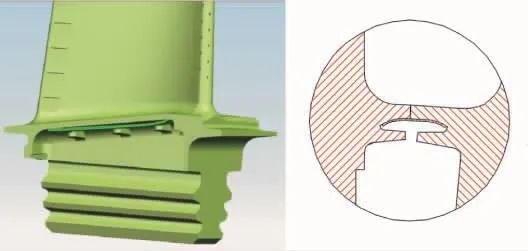
图2 阻尼片安装

2 计算方法

接触摩擦力具有强非线性，带干摩擦阻尼结构的叶片系统为强非线性系统。谐波平衡法是求解强非线性系统稳态响应问题的常用方法。动柔度法是在对非线性摩擦力进行谐波分解的基础上，对叶片有限元模型只需进行1次动态分析提取固有特性，且将问题归结为求解仅含非线性自由度的非线性方程组，大大降低了非线性迭代的计算量。

2.1 滞后弹簧摩擦模型[7]

采用的摩擦力学模型为滞后弹簧模型。这种模型实际上就是考虑了接触物体之间的变形，弹簧刚度的存在使摩擦力的变化始终滞后于相对位移的变化。

滞后弹簧物理模型及其对应的力学模型分别如图3、4所示。Fd=μN，为最大摩擦力；kd为弹簧刚度。本文研究的叶片缘板与阻尼块之间的摩擦力是1种周期性变化的力，当接触面在相对运动一段时间后，其动、静摩擦系数趋于相近，所以，在本文研究摩擦力时，假设了动、静摩擦系数相等。

设摩擦接触点之间的运动关系为x=Arcos（ωt+φ），则摩擦力Ff进行Fourier展开（只取基频谐波）

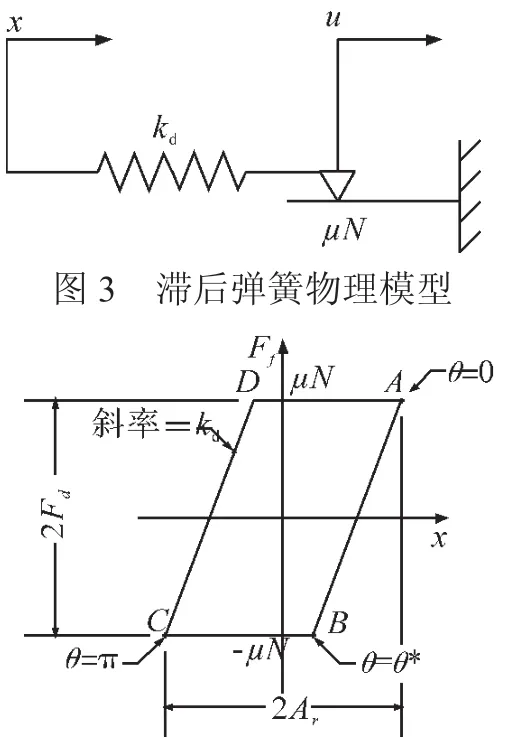
图4 滞后弹簧模型力学模型

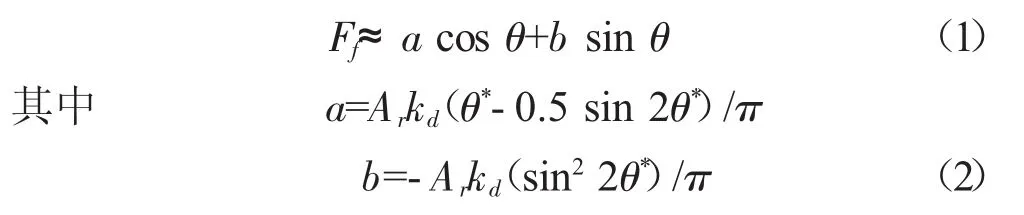
式中：θ=ωt+φ；θ*=arccos[1-2Fd/（Arkd）]；θ*∈[0，π]，当Ar≤Fd/kd时，为完全黏着状态，此时θ*=π。

2.2 求解方法[3]

设叶片－阻尼器的系统方程为

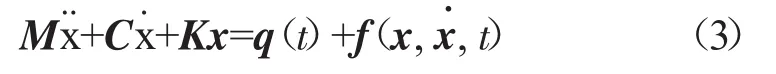
式中：M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵；x为结构自由度的振动位移向量；q（t）为作用于结构上的线性激振力；f（x,x˙,t）为接触面上产生的非线性摩擦力，是接触区振动位移与时间的函数。

叶片的激振力一般是已知的，并且是简谐形式；摩擦力由叶片的运动产生，是叶片位移的函数，一般是非线性的。为方便表示各量的相位差，用复数表示法。

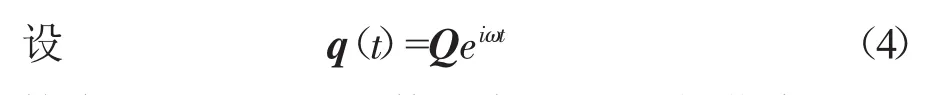
将摩擦力展成Fourier级数形式，只取基频谐波

式中：Ff为f（x,x˙,t）1阶Fourier系数；t为时间变量。

定义应力柔度：作用在节点j上的单位力引起的节点i的应力响应，记为Sij（ω），其为振动频率ω的函数。则叶片上任意一点i的应力响应为

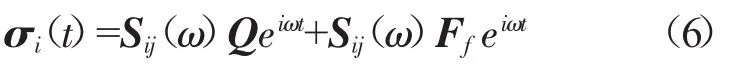
一般系统的固有频率较为分散，求解某阶固有频率附近的响应时，只要取此阶模态即可。设系统的第p阶固有频率为ωp，模态位移为Φp，模态应力为Ψp，则第p阶模态的应力柔度为

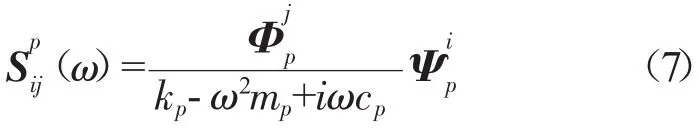
式中：mp、kp、cp为系统的第p阶模态质量、模态刚度和阻尼；为系统的第p阶模态应力的第i个分量；为系统的第p阶模态位移的第j个分量。

2.3 减振规律

对于摩擦阻尼器的正压力、接触刚度、摩擦系数等参数及激振力对叶片响应的影响，根据大量相关研究[3，8]，可总结出如下规律：

（1）存在1个最优的正压力使叶片响应最小。

（2）随着激振力的增大，其对应的最优正压力也增大，且最优正压力的取值范围变大，但各激振力对应的最优正压力下叶片峰值响应的最大降幅基本不变。

（3）随着摩擦系数的增大，其对应的最优正压力减小且取值范围变小，但最优正压力对应的最大降幅几乎与摩擦系数无关。虽然增大摩擦系数可以使最优正压力减小，但同时会导致接触面的磨损增大，因此，摩擦系数不是越大越好。

（4）随着切向刚度的增大，其对应的最优正压力也增大且取值范围变大，即增加了叶片振动的非线性程度。在相同正压力下，切向刚度越大，其峰值响应越小，减振效果越好。

（5）对于缘板阻尼器，随着相邻叶片间相位差的增大，其对应的最优正压力也增大，在相同正压力下，叶片的峰值响应均降低。最优正压力的取值范围变大，即增加了叶片振动的非线性程度。

3 减振研究

3.1 动力特性分析

为了对该带缘板摩擦阻尼片的叶片进行响应分析，首先需分析其动力特性，通过精确的有限元计算，提取出叶片的固有模态参数。

该发动机高压涡轮叶片的有限元模型如图5所示。采用10节点四面体自由网格，共划分为98105个单元，176834个节点。主要研究缘板阻尼片减振，不考虑榫头面阻尼减振，所以对榫头3对齿表面节点施加3向位移约束。榫头约束条件如图6所示。

叶片频率计算包括叶片的固有频率和考虑载荷作用下叶片变形后频率，分别计算了静止状态及发动机最大状态下叶片的固有频率。静频计算时t=20℃，动频计算时考虑叶片离心力和高温及温度差影响。叶片的频率见表1。

叶片的激振因素考虑叶片前的燃烧室喷嘴、高压涡轮导向叶片和叶片后的低压导向叶片、加力扩散器支板。该叶片主要的激振因素有9E、15E、42E和45E。得到共振分析用的坎贝尔图如图7所示。

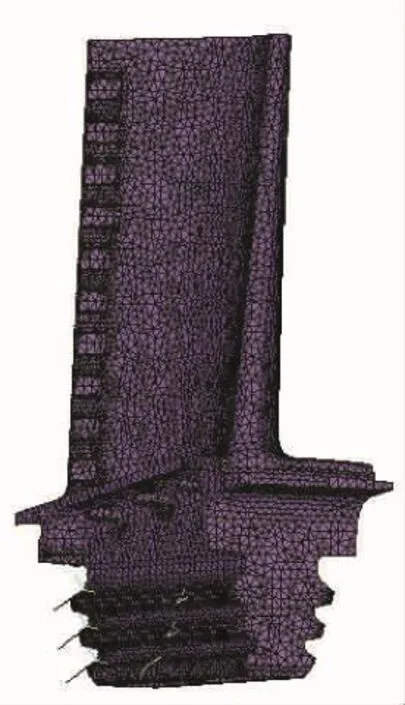
图5 叶片有限元模型

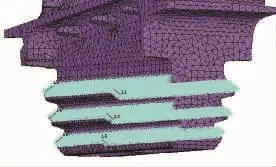
图6 榫头位移约束条件

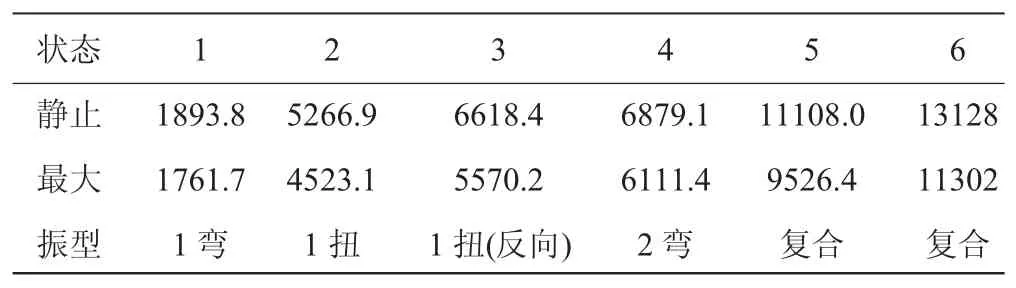
表1 前6阶振动频率Hz

图7 高压涡轮叶片的坎贝尔图

从图7中可见：

（1）第1阶频率在设计点附近，与15E、42E和45E有足够裕度。

（2）第1阶频率与15E、42E和45E的交点转速很低，在慢车转速以下。

（3）第1阶频率与9E激振频率在12000 r/m转速附近有交点。

（4）第1阶振型频率在静态下为1893.8 Hz、在台架状态下为1761.7 Hz，且随转速变化的幅度较小。

3.2接触参数的选择

（1）切向接触刚度。Hertz提出的经典球面静止接触理论在实际中被广泛应用，认为法向接触刚度可以通过2个接触物体之间的局部法向弹性变形来定义。对于相同材料组成的球面－平面接触，在压力载荷N的作用下，接触区的接触半径。其中，等效刚度；υ和E分别为材料的泊松比和弹性模量；R0为球的半径；在部分滑移状态下，切向接触刚度为，其中，G为材料的剪切模量。

（2）激振力相位差。对于循环叶片，激振力相位差为

式中：NnE为发动机转速的倍数；Nb为整圈叶片的个数。

式（8）表明：叶片间相位差取决于激振力频率与发动机转速之间的倍数以及某级叶片的个数。改变这2项参数即可改变叶片振动的相位差，而相位差的变化又使得接触点间的相对位移发生改变而影响阻尼器的减振性能。

在台架试车试验中，该发动机高压涡轮叶片1阶弯曲振动的共振转速为11600～11700 r/min,对应发动机的转速频率为193.3～195.0 Hz。1阶弯曲振动的共振频率为1761.7 Hz。故叶片的1阶弯曲振动是由发动机转速频率的9倍频所激振。实际上，这正与叶片后有9块加力扩散器支板相吻合。因该级叶片由68个叶片组成，故叶片发生1阶弯曲振动时叶片间的相位差

（3）激振力。由于叶片受到的非定常气动力难以确定，在现有文献中几乎都是假定的，通过现有涡轮平面叶栅试验数据也只能给出激振力的范围。文献[4]采用发动机台架动测得到的不加阻尼器时叶片应力响应和叶片模态应力的比值为依据来确定激振力的幅值。但本文研究的涡轮叶片在发动机动测时已经装有阻尼片，无法得到不加阻尼器时叶片的应力响应幅值。因此，本文先用涡轮平面叶栅试验数据给出激振力占气动力的百分比范围，再用发动机台架动测得到的已安装阻尼片的叶片应力响应，计算叶片受到的激振力。

在涡轮平面叶栅试验中，不同出口马赫数下的出口栅距方向上总压恢复系数如图8所示，这里采用了无量纲的参数分别来描述总压。从图8中可见，随着出口马赫数的增大，叶栅尾迹逐渐变大。出口马赫数为0.6时气动力的波动为4.5%，且随着出口马赫数增大气动力波动增加，该高压涡轮出口马赫数平均值约为0.55，差值得到此时气动力波动为4.1%。对轴向分力而言，尾迹干扰引起的波动幅值比势流干扰的高15%[9]，则势扰动引起气动力波动为3.5%。又由于高压涡轮转子后有低压涡轮减弱加力扩散器支板势扰动对叶片气动力的影响，所以激振力为叶身稳态气动载荷的3.5%以下。

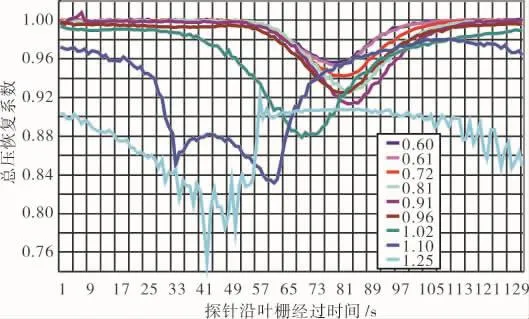
图8 不同出口马赫数下总压恢复系数沿栅距分布

台架动应力测量结果：动测点为1弯振动主疲劳源区，最大应力是10 MPa，转速为11675 r/min，振动频率约为1650 Hz。实际装配的阻尼片在该转速下每个摩擦点对间的正压力约为60 N。动测点应力响应随激振力变化（正压力60 N）如图9所示。采用动测点为计算点，为使用自行编写的软件根据有限元计算的该叶片模态应力，得到不同激振力下的应力响应。

该故障叶片气动载荷通过叶片S1流面气动参数计算。当激振力为气动载荷的0.68%时应力与台架试车测得的应力值相等。满足激振力为叶身稳态气动载荷的3.5%以下，所以，认为取激振力为气动力的0.68%是合理的。

其他参数：摩擦系数只与接触面材料和表面膜状态有关，在工程近似计算中，将摩擦系数看成在滑动过程中不变是允许的。选取缘板摩擦阻尼器接触面摩擦系数为0.3。对于现代叶片常用的材料（钛合金和镍基合金），其材料阻尼比非常低，本文计算涡轮叶片1弯振型时黏性阻尼比为0.003。

3.3 计算结果及分析

采用上述阻尼片参数计算叶片1阶弯曲响应，计算点应力峰值响应随正压力的变化曲线如图10所示。

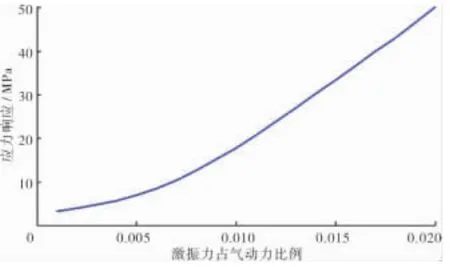
图9 动测点应力响应随激振力变化（正压力60 N）

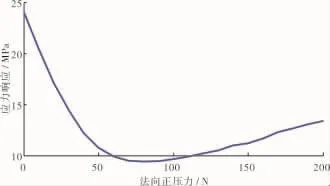
图10 应力响应随正压力变化曲线

从图10中可见，正压力在60～110 N时阻尼结构均有很好的减振效果，计算点振动应力峰值减小到不加阻尼片时的40%左右。可以认为在60 N正压力时，其阻尼结构减振效果处在较好的范围内，即现有的阻尼片质量是合理的。在装配时保证阻尼片在叶片缘板与伸根间为自由状态，即可起到很好的减振效果。

当正压力为80 N时对应的计算点应力幅值最小，即为最优正压力，计算点应力为9.416 MPa，比正压力60 N时计算点应力的9.945 MPa减小了5.6%，此时的阻尼片质量为实际安装的阻尼片质量的1.33倍。适当增加阻尼片质量可达到更好的减振效果。但同时要考虑阻尼片质量增加使整机质量增加和引起强度变化的问题。

4 结论

通过平面叶栅试验数据和发动机台架动测数据估算激振力占气动力的百分比，用得到的激振力计算了叶片稳态应力响应。数值计算结果表明：

（1）现有的阻尼片质量在比较合理的范围内，在安装阻尼片时，只要保证其自由状态就能在原共振转速时起到很好的减振效果。

（2）可适当增加阻尼片质量以增大故障转速下阻尼片与缘板间的正压力，减小振动应力，提高阻尼结构的减振效果。

[1]Panning L,Sextro W,Popp W.Optimization of inter-blade fricion damper design[R].ASME 2000-GT-0541.

[2]Panning L,Popp K,Sextro W,et al.Asymmetrical underplatform dampers in gas turbine bladings:theory and application [R].ASME 2004-GT-53316.

[3]郝燕平.带摩擦阻尼叶片的动力响应和减振研究[D].北京：北京航空航天大学，2001. HAO Yanping.Investigation on the vibratory response of blade and vibration control with friction damper[D]Beijing：Beihang University，2001.(in Chinese)

[4]漆文凯.摩擦阻尼减振设计中的局部滑动问题[J].航空学报，2006，27（5）：805-809. QI Wenkai.Microslip study on friction damping and its application in design of vibration reduction[J].Acta Aeronautica et Astronautica Sinica，2006，27（5）:805-809.(in Chinese)

[5]何尚文，任兴民，秦卫阳，等.基于整体-局部统一滑动模型的叶片缘板阻尼器减振特性分析[J].西北工业大学学报，2010，28（6）：872-876. HE Shangwen，REN Xingmin，QIN Weiyang，et al.A method for reducing the blade vibration of platform damper using the macro-microslipmodel[J].JournalofNorthwestern Polytechnical University，2010，28（6）：872-876.(in Chinese)

[6]Koh K H，Griffin J H，Filippi1 S，et al.Characterization of turbine blade friction dampers[R].ASME 2004-GT-53278.

[7]郝燕平，朱梓根.带摩擦阻尼的叶片响应求解方法[J].航空学报，2001，22（5）:411-414. HAO Yanping，ZHU Zigen.New method to resolve vibratory response of blades with friction damping[J].Acta Aeronautica et Astronautica Sinica，2001，22（5）：411-414.（in Chinese）

[8]Cook R M.Airfoil vibration dampers program(final report)[Z]. NASB-35720.

[9]李绍斌，苏杰先，冯国泰，等.高负荷跨声速压气机动静叶干扰下叶片气动负荷研究[J].推进技术，2006，27（5）：410-415. LI Shaobin，SU Jiexian，FENG Guotai,et al.Investigation of the unsteady aerodynamic blade loads in a highly loaded transonic compressor stage[J].Journal of Propulsion Technology, 2006，27（5）：410-415.(in Chinese)

[10]孙莹.干摩擦阻尼减振技术在叶片结构设计中的应用研究[D].北京：中国航空研究院，2013. SUN Ying.Research on application of dry friction damping technology for blade vibration reduction design[D].Beijing：Chinese Aeronautical Establishment，2013.(in Chinese)

[11]于达仁.动态系统中干摩擦力的数值计算模型[J].哈尔滨工业大学学报，1995，27（5）：41-45. YU Daren.Numerical model of dry friction force in dynamic system.JournalofHarbinInstituteofTechnology[J]. 1995，27（5）：41-45.(in Chinese)

[12]任勇生，李俊宝，熊诗波，等.干摩擦阻尼及其在工程结构被动减振设计中的应用研究[J].力学与实践，1997，19（2）：12-17. REN Yongsheng，LI Junbao，XIONG Shibo，et al.Dry friction damping and its application research of vibration reduction in engineering structure[J].Mechanics and Practice，1997，19（2）：12-17.

[13]季葆华，张乐天，袁奇.汽轮机叶片干摩擦阻尼机及其数学描述[J].汽轮机技术，1997，39（6）：345-349. JI Baohua，ZHANG Letian，YUAN Qi.The mechanism and mathematic description of dry friction damping of steam turbine[J].Turbine Technology，1997,39（6）：345-349.(in Chinese)

[14]单颖春，郝燕平，朱梓根，等.干摩擦阻尼块在叶片减振方面的应用与发展[J].航空动力学报，2001，16（3）：218-223. SHANYingchun,HAOYanping,ZHUZigen,etal. Application and development of platform friction damper for depressing resonant vibration of blade[J].Journal of Aerospace Power，2001，16（3）：218-223.(in Chinese)

Vibration Reduction of High Pressure Turbine Blade with Platform Friction Damper

SUN Ying,LIU Yong-quan,HAO Yan-ping,ZHANG Jun-feng
（AVICShenyangEngineDesignandResearchInstitute,Shenyang110015,China）

Dry friction damping is a very effective method to reduce the vibration response of aeroengine blades,which can effectively limit the vibration stress level of the blade.Aiming at the high pressure turbine blade with the platform damper,a method of aerodynamic calculated exciting force was proposed,and the influence parameters were analyzed by the harmonic balance method combined with dynamic flexibility method based on the hysteretic spring model.The stress response was calculated on the blade,optimum stress made the blade vibration stress,and the damper mass was optimum analyzed.The results show that the increase of damper mass can improve the results of vibration reduction in a reasonable range.

high pressure turbine;blade;platform;vibration;exciting force;dry friction;damping;aeroengine

V 231.92

A

10.13477/j.cnki.aeroengine.2014.05.011

2013-01-29基金项目：国家重大基础研究项目资助

孙莹（1987），女，硕士，研究方向为航空发动机结构强度与振动；Email：444959317@qq.com。

孙莹，刘永泉，郝燕平，等.带缘板阻尼片高压涡轮叶片的减振研究[J].航空发动机，2014，40（5）:57-61.SUN Ying，LIU Yongquan，HAO Yanping，et al.Vibration reduction ofhigh pressure turbine blade with platformfriction damper[J].Aeroengine，2014，40（5）:57-61.