考虑表面加工缺陷的轮盘疲劳寿命分析方法

陆山，李波

（西北工业大学动力与能源学院，西安710072）

考虑表面加工缺陷的轮盘疲劳寿命分析方法

陆山，李波

（西北工业大学动力与能源学院，西安710072）

为了将表面加工状态引入零构件概率寿命分析中，提出并建立了考虑表面加工缺陷的轮盘疲劳寿命分析方法。将孔的表面加工缺陷简化为表面裂纹和/或角裂纹，导出裂纹深度密度函数；借助裂纹应力强度因子经验公式及有限元分析，提出轮盘孔边裂纹应力强度因子计算的推广经验公式方法。建立了3种考虑表面缺陷尺度分布时轮盘概率寿命计算方法。以钛合金盘为例，在获得的表面缺陷分布条件下，计算了给定寿命的轮盘疲劳寿命失效概率及故障率。仿真结果表明：采用该方法可以将表面加工缺陷对疲劳寿命的影响引入构件寿命评估体系。

表面加工缺陷；疲劳寿命；应力强度因子；裂纹扩展；失效概率；故障率；轮盘

0 引言

轮盘是航空发动机最重要的承力构件之一，结构复杂，成本昂贵，工作条件恶劣，一旦损坏，后果往往是灾难性的。轮盘在服役期间承受着重复作用的疲劳载荷，其设计必须遵守相关结构的强度准则，要求具有足够的低循环疲劳寿命，以及损伤容限特性，来满足可靠性和耐久性[1]。在发动机轮盘的实际加工中，会不可避免地产生加工缺陷，如果在应力危险部位（特别是在盘的孔边）出现了明显的加工缺陷，则可能会对其寿命产生较大影响。因此，在轮盘寿命预测时，应该考虑加工刀痕对寿命的影响，这也是轮盘损伤容限设计要求研究的内容。在分析轮盘表面加工缺陷的微观表象之后，可以将轮盘孔边的加工刀痕作为裂纹来处理[1-2]，裂纹的深度即为加工刀痕（缺陷）的深度，而裂纹的扩展寿命，则在一定程度上代表了轮盘的疲劳寿命。裂纹应力强度因子可以通过经验公式[3]、有限元法[4-5]或边界元法[6]求解。然而经验公式法仅适用于简单载荷下的简单几何构件；零件加工缺陷的深度是不确定的，具有一定的随机性，如果要大量计算轮盘上不同裂纹应力强度因子，文献[4-6]中的数值方法难以直接使用。目前已有针对体内分布夹杂的轮盘概率寿命分析方法[7-9]，但考虑表面分布缺陷的轮盘概率寿命分析方法目前在国内文献中尚未查到，国外相关研究文献也极少，且仅给出表面缺陷深度超越概率[2,10]，及盘孔边概率寿命分析框架[2]。

本文针对加工缺陷深度的随机性，导出了表面缺陷深度密度函数；利用有限元分析给出1种快速计算某类表面裂纹应力强度因子的方法；在此基础上，提出基于危险部位分布深度表面缺陷的轮盘低循环疲劳寿命可靠性分析方法。

1 表面加工缺陷及其分布

表面缺陷是指在机械加工中在零件表面形成的局部切除或遗留材料的痕迹。其分布形式将直接影响零件寿命的可靠性。不同的缺陷深度分布形式，其寿命可靠度也不同。目前，中国尚无表面缺陷的国家标准和部颁标准，仅在表面粗糙度中有定性而无定量的说明[11]。

在可以查到的参考文献中，表面缺陷的分布规律主要有Weibull、高斯以及指数分布[2，10]3种模型。事实上，Weibull分布可以退化成指数分布。

在美国联邦航空管理局（FAA）的报告[2]中，仅给出了钛、钢、镍或镍基粉末冶金发动机转子上的圆孔，由机械加工引起的表面缺陷的初始分布的性质用单位表面面积超过特定尺寸深度的缺陷数量F′来表示[2]

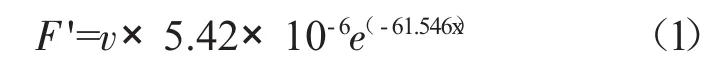
式中：x为缺陷深度（inch）；v为频度系数，大小与轮盘上孔的深度和直径比有关。

为了获得缺陷的密度函数，令x=0，则F′|x=0=5.42×10-6v，表示在单位面积上（深度大于0）所有缺陷的数量，那么缺陷深度超过x的概率为

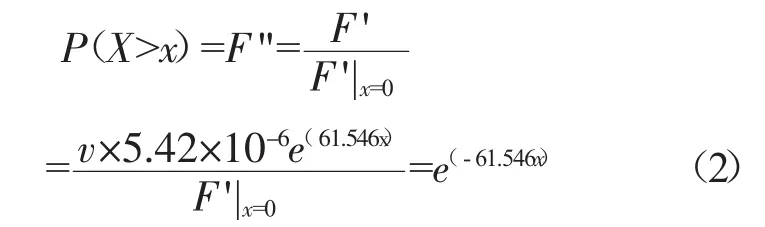
根据累积分布函数的定义，缺陷深度分布的累积分布函数F的表达式为

对其微分即得到缺陷深度分布的概率密度函数

可以看到，该指数分布为1个退化的Weibull分布。事实上依加工方式、精度以及表面处理方式不同等，甚至在零件的不同部位，最终的表面缺陷的深度分布形式也可能有所不同，但本文第3章建立的考虑表面缺陷分布的轮盘概率寿命分析方法是通用的。

2 表面裂纹的SIF计算

裂纹应力强度因子（SIF）可以通过有限元法建模计算，但是计算1次需消耗较多人工建模时间和机时。而本文需要计算大量不同尺度的裂纹SIF，并且在裂纹扩展分析过程也需要大量的裂纹应力强度因子计算。如果有相应的经验公式计算SIF，可以节省很多时间。

通常表面缺陷如果发生在零件的边角和表面上，可分别采用角裂纹和表面裂纹模型。文献[3]中已给出角裂纹和表面裂纹的应力强度因子计算经验公式，甚至对于容易产生应力集中的孔边，也给出了相应的应力强度因子计算公式。孔边角、表面裂纹形式分别如图1、2所示。

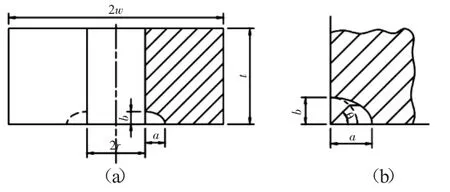
图1 孔边角裂纹

图2 孔壁表面裂纹

具体SIF计算公式可以直接查询手册[3]，只是手册中一般裂纹的载体比较简单，均为带孔或无孔的等厚板，加载的方式一般为远场单向均匀拉伸。但根据圣维南原理，远处的应力场对于需要着重考虑的部位的SIF影响不大，因此只要保证裂纹临近的主应力分布大小吻合，即可得较为满意的SIF结果。

本文结合第4章典型算例分析，提出结合有限元应力分析和表面半圆形裂纹和孔边角裂纹的经验公式，计算轮盘孔边应力强度因子的推广经验公式方法。其主要步骤是：首先，选取包含1个孔的轮盘循环对称子模型，进行无裂纹模型应力分析；其次，利用轮盘循环对称子模型厚度、弦长特征尺寸，建立方形带孔板无裂纹模型，并在单向均布载荷下进行应力分析；再次，由轮盘循环对称子模型孔边危险点与方形带孔板模型孔边危险点第1主应力相等条件，确定方形带孔板无裂纹模型的单向均布载荷σm；最后，由确定的σm和矩形带孔板孔边裂纹经验公式，计算一系列裂纹尺寸下盘孔边表面或角裂纹应力强度因子。

3 给定分布裂纹深度下裂纹扩展寿命计算

对含单裂纹的轮盘结构裂纹扩展模型，采用简单实用的Paris公式[12]

式中：ΔK=Kmax-Kmin，即应力强度因子的幅值；C、p为通过试验得出的材料常数，与材料、试样厚度、应力比、载荷频率等有关。

由于本文实际采用的裂纹应力强度因子计算经验公式形式复杂，无法直接积分，所以，采用1种分步裂纹扩展、寿命叠加的计算方法。即在初始裂纹深度的基础上，计算应力强度因子，并给定1个微小裂纹扩展量da，利用Paris公式计算相应的裂纹扩展寿命dN；再在新的裂纹深度下计算新的应力强度因子，一直循环到最终的应力强度因子到达断裂韧性Klc，或者最终的裂纹深度到达临界裂纹尺寸。至此，叠加各步所有寿命增量dN即得到裂纹扩展总寿命。

为简化计算，本文的裂纹模型被简化为半圆形或者圆形裂纹，应力强度因子的大小沿裂纹前沿是不同的。在计算中，每次选择沿裂纹前缘最大的应力强度因子进行扩展分析，扩展后的模型仍按半圆形或圆形裂纹进行计算，最终结果偏于安全，并且简化了计算模型。对于表面裂纹来说，其深度尺寸理论大于0，且小于某一确定值。然而在工程实际中，当裂纹尺寸小于一定值时，可以分析认为此裂纹扩展寿命是无限寿命，或者说其寿命已远大于规定的要求（本文中把裂纹扩展寿命大于一般寿命要求3个量级左右时的初始裂纹尺寸定义为amin=a0）；而当裂纹尺寸大于某值时，可以认为零件从生产出时已经失效，即寿命为0（本文中把裂纹未扩展前的应力强度因子已经大于材料的断裂韧性左右时的尺寸定义为ama）x。

在建立单裂纹扩展寿命分析模型之后，可以采用3种方法来计算构件基于分布尺寸下的裂纹扩展寿命可靠度。

3.1 概率求和法

选定裂纹尺寸的上限amax和下限amin，将其分为若干小区间，对每个区间内的裂纹尺寸，进行裂纹扩展分析，计算得到不同尺寸裂纹的扩展寿命t（a），将其与给定的设计寿命下限进行比较，如果大于给定寿命要求，则将该尺寸下的可靠度R（a）定义为1，如果不满足要求则定义为0。

根据裂纹尺寸的分布，可以计算尺寸为a时的概率密度值为f（a），那么分布尺寸下裂纹扩展寿命的可靠度R为

因R2无法直接积分，所以一般利用数值积分方法来计算。将裂纹尺寸的区间细分为多段，计算各小段的f和相应的R，从而得到1个Ri。对Ri求和，再与R1相加即得零件给定部位的给定寿命可靠度R。需要注意的是，对于不同的寿命准则T，会出现不同的amin；如果T较小则amin较大，那么会减少相当一部分计算量。

3.2 蒙特卡洛法

根据裂纹尺寸分布的概率密度函数，可以生成1个相应的随机数序列，即一系列的裂纹深度。对1个裂纹深度进行扩展寿命分析，当裂纹尺寸小于之前所述的amin，可以直接将裂纹的寿命定为1个极大值（大于寿命要求T即可）；当裂纹尺寸大于amax，可以将裂纹的寿命定义为0；其他尺寸的裂纹利用裂纹扩展计算公式计算。如果计算所有的随机数并不会影响最终结果，上述处理方法只是为了减少一部分计算量，从而节省了计算时间。

将各裂纹扩展寿命计算完成之后，根据可靠度的定义，给定寿命的可靠性R的计算公式

3.3 超越概率法

超越概率法是直接利用裂纹深度尺寸的超越概率，即

假设1个深度尺寸为x0的裂纹，则其余裂纹深度尺寸超过x0的概率为e（-61.546x）。通过裂纹扩展计算得到深度为x0的裂纹扩展寿命为N0，那么全部尺寸下裂纹的扩展寿命N中

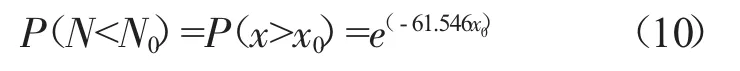
由可靠度定义

R=1-P（N＜N0）=1-P（x＞x0）=1-e（-61.546x）0=1-F"|x=x0=F|x=x0

由以上推导可知，当已知设计寿命要求对应的裂纹深度尺寸时，利用尺寸分布的累积密度函数，可直接得到含刀痕构件的寿命可靠度。

在上述3种方法中，除了裂纹深度尺寸外，其他参数都是确定性的，即没有考虑分散性。然而事实上，裂纹扩展模型、载荷、结构的尺寸等都可能具有一定的分散性。如果要考虑这些分散性，蒙特卡洛法较其他2种方法是易用性最强的办法。

4 典型算例分析

1个钛合金等厚盘，外径为0.830 m，内径为0.6 m，盘上有40个直径为0.0127 m的圆孔，均布在半径为0.3625 m的圆上。盘厚0.0254 m。在0—5700—0 r/min等幅循环三角转速谱作用下，进行20000次循环。在峰值转速下轮缘作用均布外载荷为33 MPa，以模拟叶片载荷[2]。

盘的材料数据分别为密度ρ=4.450 kg/m3，杨氏模量E=120 GPa，泊松比μ=0.361，断裂韧性KIC=64.5，应力比为0的裂纹扩展率（9.25E-13）×（ΔK）3.97[2]。

首先建立1/40盘的有限元模型，进行应力分析，得出盘孔边应力的大小及分布，周向应力分布如图4所示。

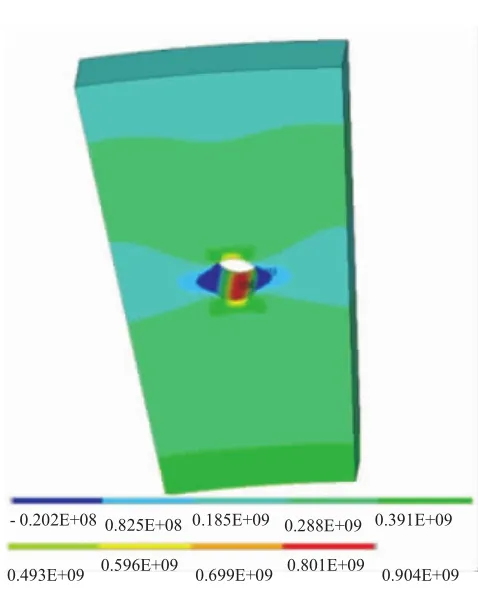
图4 轮盘周向应力结果

孔边最大周向应力为904 MPa，在孔壁表面沿厚度方向中心处6点钟位置。在轮盘扇段模型上，分别在孔边和孔壁中间建立深度均为0.00254 m裂纹的有限元模型，并进行计算分析，可以得到孔边角裂纹沿圆周最大应力强度因子为，孔壁表面裂纹沿圆周的最大应力强度因子为42.722 MPa■m 。

为模拟裂纹扩展过程，需要建立适用于轮盘孔边裂纹应力强度因子计算经验公式的方法。选用文献[3]中带孔等厚板的孔边角裂纹及孔内表面裂纹的应力计算公式。取等厚板的厚度与等厚盘厚度一致，宽度和高度取盘孔心处半径Rbh的圆周长的1/40，模型2条对边施加均布载荷300 MPa。有限元分析结果如图5所示。

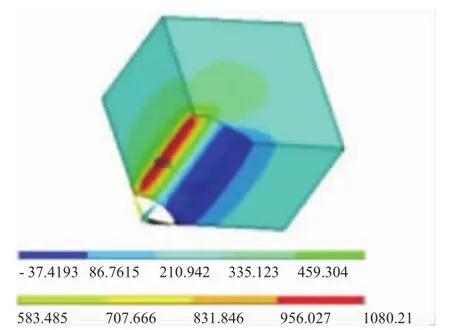
图5 带孔等厚板周向应力结果

从图5中可见，孔边与无裂纹盘孔边的应力分布基本一致。孔边最大应力为1080 MPa，应力集中系数为1080/300=3.6。那么当利用等厚盘孔边角裂纹及孔内表面裂纹的应力强度因子计算公式计算轮盘孔边裂纹时，应代入经验公式的远场应力值为904/3.6=251.1 MPa；同时代入裂纹深度尺寸0.00254 m，进行应力强度因子的计算，最终结果见表1。

表1 应力强度因子（SIF）解对比

从表1可见，利用推广的经验公式得到的SIF结果与有限元分析得到的结果误差小于3.5%。而直接利用经验公式计算则摆脱了大量有限元建模计算分析过程，可以直接利用MATLAB编程计算，极大地缩短了计算时间。

确定了裂纹应力强度因子计算公式之后，可以直接根据缺陷分布，分别利用上述提出的3种不同方法计算得到轮盘20000次循环谱下的失效概率和故障率。需要注意以下事项。

（1）取孔边角裂纹和表面裂纹的断裂概率中较差的作为孔的断裂概率；

（2）缺陷分布定义是单位面积上的，因此最终计算结果需要乘以同一加工方式所加工的表面积，算例中即为40个孔的内表面面积；

（3）FAA报告[2]中指出在轮盘断裂概率计算中，对孔的制造采用信任度的方法，需要将计算结果除以信任度。FAA报告中给出的可用信任度包括30、35、40[2]；

（4）得出单个孔的断裂概率之后，计算盘的断裂概率时，40个孔之间为串联关系，采用可靠度连乘公式直接计算即可。

（5）在得到盘的断裂失效概率之后，可以通过数值微分办法计算出盘在给定寿命下的概率密度值，除以可靠度后即故障率。

由3种不同方法得到的20000次循环的失效概率和故障率分别见表2、3。

表2 3种方法的失效概率

表3 3种方法的故障率

概率求和法与超越概率法的误差主要产生于计算时裂纹区间内的间隔，因此二者的计算结果非常接近；而蒙特卡洛法的误差主要产生于随机数发生的数量。当概率求和法与超越概率法计算的裂纹间隔足够小，并且蒙特卡洛法中的随机数足够多时，这3种方法得到的结果将趋于同一准确值。采用超越概率法时，无需对所有尺寸的裂纹进行扩展，只需要利用二分法的思想，不断搜索得到要求的设计寿命对应的裂纹深度尺寸；而概率求和法则需要对全部尺寸的裂纹进行扩展分析；蒙特卡洛法则可以根据精度需要控制不同深度的裂纹数量。文献[2]中给出了本算例的故障率风险为2.88E-4，本文的计算结果与其相差1.758～3.570倍。

5 结束语

本文首先将表面加工痕迹简化为裂纹，导出裂纹深度密度函数；提出利用经验公式，结合有限元应力分析计算复杂结构孔边裂纹应力强度因子的推广经验公式方法。然后建立了给定分布下表面裂纹扩展寿命可靠度的3种计算方法。以带孔钛合金盘为例，采用推广的经验公式方法计算孔边应力强度因子误差小于3.5%；在分布表面缺陷条件下，计算并验证得到了给定设计寿命下的盘孔边失效概率和故障率，采用3种概率寿命积分方法所得计算结果相互吻合。

研究结果表明：本文所述方法可将零件表面加工缺陷引入轮盘疲劳寿命分析方法体系，简单有效，并可推广应用于考虑分布尺寸加工刀痕裂纹的其他结构的疲劳概率寿命分析中，为发动机结构损伤容限分析提供了新的方法。

[1]航空航天工业部科学技术研究院.损伤容限设计手册[S].西安：西北工业大学出版社，1989. Science and Technology Establishment of Ministry of Aerospace Industry.Damage tolerant design handbook[S].Xi’an：Northwestern Polytechnical University Press,1989.（in Chinese）

[2]U.S.Department of Transportation Federal Highway Administration.Damage tolerance of hole features in high energy turbine engine rotors[R].AC 33.70-2,2009.

[3]中国航空研究院.应力强度因子手册[S].北京:科学出版社，1993. Chinese Aeronautical Establishment.The manual of stress intensity factor[S].Beijing:Science Press,1993.（in Chinese）

[4]谢伟，屠少威，黄其青，等.铆钉填充锪窝孔边角裂纹应力强度因子分级[J].西北工业大学学报，2012，30（4）：524-528. XIE Wei,TU Shaowei,HUANG Qiqing,et al.Some useful results of investigation on stress intensity factors(SIFs)of corner crack at rivet-filled countersunk hole[J].Journal of Northwestern Polytechnical University，2012，30（4）：524-528.（in Chinese）

[5]唐俊星，陆山.三维裂纹整体参数化模化方法[J].航空动力学报,2008，23（4）：737-741. TANG Junxing,LU Shan.A integral parameter based modeling method for 3D crack[J].Journal of Aerospace Power,2008，23（4）：737-741.（in Chinese）

[6]陆山，黄其青.涡轮盘销钉孔损伤容限分析新方法及其应用[J].航空动力学报，2002，17（1）：87-92. LU Shan，HUANG Qiqing.New method and its application for damage tolerance analysis of turbine disk’s pin hole[J].Journal of Aerospace Power,2002，17（1）：87-92.（in Chinese）

[7]蒋向华，杨晓光，王延荣.一种结构可靠性的数值计算方法[J].航空动力学报，2005，20（5）：778-782.JIANG Xianghua,YANG Xiaoguang,WANG Yan rong.Numerical approach for structure reliability evaluation[J].Journal of Aerospace Power，2005，20（5）：778-782.（in Chinese）

[8]魏大盛，杨晓光，王延荣.基于缺陷分布形式的粉末冶金涡轮盘可靠度计算模型[J].机械工程学报，2008，44（11）：132-137. WEI Dasheng，YANG Xiaoguang，WANG Yanrong.Model for calculating the reliability of powder metallurgy turbine disk based on distribution of defects[J].Chinese Journal of Mechan ical Engineering，2008，44（11）：132-137.（in Chinese）

[9]唐俊星.含夹杂粉末盘概率寿命三维仿真方法与应用[D].西安：西北工业大学，2008. TANG Junxing.3D simulation method of probabilitic life of powder methallurgy disk containing inlusions and application [D].Xi’an：Northwestern Polytechnical University,2008.（in Chinese）

[10]Richard C，Michael G，Darryl L.The development of anomaly distributions for machined holes in aircraft engine rotors[C]// ASME Turbo Expo,Spain，2006.

[11]张泰昌.表面缺陷与表面粗糙度的区分及其评定[J].计量测量技术，1990（2）：30-31. ZHANG Taichang.The difference and assessment between surface anomaly and surface roughness[J].Metrology Test Technology，1990（2）：30-31.（in Chinese）

[12]李庆芬，胡胜海，朱世范.断裂力学及其工程应用[M].哈尔滨：哈尔滨工程大学出版社，1997：87. LI Qingfen，HU Shenghai，ZHU Shifan.Fracture mechanics and the engineering application[M].Harbin：Harbin Engineering University Press，1997：87.（in Chinese）

An Analysis Method of Disk Fatigue Life Considering Surface Manufacturing-Induced Anomaly

LU Shan,LI Bo
（School of Power and Energy,Northwestern Polytechnical University,Xi'an 710072）

In order to analyze the aeroengine components′life at the surface manufacture state,a method for disk fatigue life analysis considering surface manufacturing-induced anomaly was presented and built.The surface manufacturing anomaly was simplified as surface cracks and/or corner cracks,and the crack density function was exported.Using the empirical formula of Stress Intensity Factor(SIF)and FEM analysis,a popularized empirical formula method to compute the SIF of a crack at hole edge of a disk was proposed and verified by FEM solution.Three methods to calculate the probabilistic life of disk considering the depth distribution of surface anomaly were built. Taking a titanium disk as an example,the failure risk and failure rate at a given life was computed,under the conditions of the gained distribution of surface anomaly.The simulation results show that the surface manufacturing-induced anomaly affeots fatigue life can be introduced in components'life assessment life by this method.

surface manufacturing-induced anomaly;fatigue life;stress intensity factor;crack propagation;failure risk;failure rate;disk

V 231.95

A

10.13477/j.cnki.aeroengine.2014.05.002

2014-03-10

陆山（1955），男，教授，博士生导师，研究方向为航空发动机结构强度和构件寿命可靠性数值分析及试验评估技术；E-mail：shanlu@nwpu.edu.cn。

陆山，李波.考虑表面加工缺陷的轮盘疲劳寿命分析方法[J].航空发动机，2014，40（5）：7-12.LU Shan，LI Bo.An analysis method of disk fatigue life consideringsurface manufacturing-induced anomaly[J].Aeroengine，2014，40（5）：7-12.