水中有限长圆柱壳体辐射声场特性
武国启
(大连测控技术研究所,辽宁大连116013)
水中有限长圆柱壳体辐射声场特性
武国启
(大连测控技术研究所,辽宁大连116013)
理论研究有源点激励时水中有限长圆柱壳体辐射声场特性。根据圆柱壳体耦合振动理论,推导有源点激励时水中有限长圆柱壳体振动速度与辐射声压计算式,计算并分析有源点激励时水中有限长圆柱壳体振动速度分布特征、声辐射近场和远场特性。研究结果表明:随着结构阻尼增大,圆柱壳体振动能量与声辐射能量向激励点处集中,且频率越高,这种集中效应越显著。在声辐射近场,声压衰减较快,其分布规律与壳体振动分布规律相近;在声辐射远场,声压衰减规律近似为球面波衰减,声压分布具有一定指向性,且激励力作用方向为声辐射主要方向。
圆柱壳体;辐射声场;有源激励;结构阻尼;集中效应
0 引言
水中有限长圆柱壳体结构是水下航行器的基本结构形式,研究其振动与声辐射特性对水下航行器振动噪声测试具有重要实际意义。关于有限长圆柱壳体声- 振特性研究,Junger[1]系统总结了 Stepanishen[2]和Sandman[3]等研究成果,根据圆柱壳体耦合振动理论,建立了有限长圆柱壳体振动和声辐射的理论计算模型。Laulagnet[4],Guyader[5]与 Wang[6]在 文 献 [1]的基础上,研究了有限长圆柱壳体声辐射功率与辐射效率。对于加肋圆柱壳体声-振特性研究,Laulagnet、Harari、汤渭霖、廖长江[7-10]分别建立了有限长加肋圆柱壳体声-振理论计算模型,并分析了加肋对有限长圆柱壳体声辐射功率及效率的影响。金广文[11]通过双层加肋圆柱壳体模型水下振动试验,研究了不同激励条件下内外壳体振动特性,建立了水下双层圆柱壳体有限元模型,计算分析了壳体在流固耦合条件下的振动路径及特性。
关于水中有限长圆柱壳体振动与声辐射研究,主要集中在声-振理论计算模型建立、声辐射功率与效率影响因素分析,缺乏振动与声辐射关系及辐射声场特性系统研究。对于水中有限长加肋圆柱壳体,低频激励时加肋对辐射声场影响较小,此时可简化为无肋壳体。本文前期工作采用圆柱壳体耦合振动理论,建立有源点激励水中有限长圆柱壳体声辐射数学模型,分析无阻尼条件圆柱壳体辐射声场特性[12]。在此基础上,建立水中有限长圆柱壳体有阻尼条件振动速度与辐射声压数学模型,进而计算分析结构阻尼对壳体振动速度与辐射声场的影响关系,获取壳体振动速度、辐射声场的变化规律,及二者之间的对应关系。
1 理论分析
图1为两端面分别简支在刚性无限长圆柱形障板上的水中有限长圆柱壳体,圆柱壳体结构参数:长度为2L,半径为a,厚度为h,且h/a<<1。材料密度为ρp,弹性模量为E,泊松比为μ,水的密度和声速分别为ρ0和c0,波数k0=ω/c0,其中ω为圆频率。
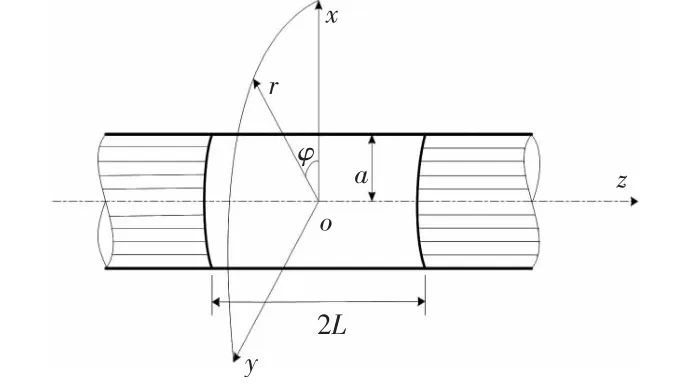
图1 水中有限长圆柱壳体Fig.1 Cylindrical shell with finite length in water
采用 Donnell壳体理论,则圆柱壳体运动方程为[1]:

式中:z,φ,r分别为轴向、周向和径向坐标;u,v,w分别为振动在坐标方向的位移;Fr和pa分别为径向点力和壳体表面压力;cp为圆柱壳体纵波速度;β2为圆柱壳体厚度因子。其表达式分别为:

当材料具有阻尼时弹性模量为复数,即:

其中η为阻尼因子。
圆柱壳体在水中的耦合振动可用模态法求解,即:

作用于壳体径向激励力和表面声压用模态形式表达为:

式中Fmn和pmn分别为径向模态力和表面模态声压。
将式(2)~式(4)代入式(1),可得圆柱壳体耦合振动模态方程:



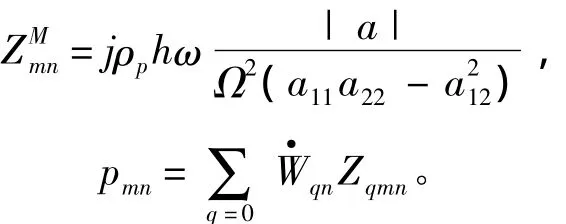
式中Zqmn为 (q,n)阶和 (m,n)阶模态互辐射阻抗,计算式为[13]:

为波数域γ的声辐射阻抗。
由式(6)可推出忽略互耦合时的圆柱壳体径向振动模态速度,即:

由式(3)可得径向模态力Fmn计算式:

由式(2)和式(7)可得圆柱壳体径向振动速度为:

其振动速度级Lw定义为:

式中基准速度˙w0=5×10-8m/s。
由式(7)可得水中有限长圆柱壳体辐射声压,即:

其声压级Lp定义为:

式中基准声压p0=10-6Pa。
2 计算结果分析
选取圆柱壳体基本参数为:L=5 m,a=4 m,h=0.02 m,ρp=7 800 kg/m3,E0=2.16 ×1011N/m2,μ =0.3,η =0.001,0.01,0.1。当阻尼因子不变时,其值设为η=0.01。水介质基本参数:ρ0=1 000 kg/m3,c0=1 500 m/s。设作用于圆柱壳体简谐点力为Frz,φ,()a,则:

其中,激励力幅值F0=10 N,20 N,当激励力幅值不变时,其值设为F0=10 N。下面分别对有源单点激励和多点激励圆柱壳体辐射声场进行计算分析。
2.1 有源单点激励
设单点激励时径向力作用点为 (0,0,a),则由式(8)和式(11)可得模态力的计算式:

将式(12)代入壳体振动速度与辐射声压计算式,可计算出单点激励时径向振动速度与辐射声压,结果如图2~图4所示。
从图2可知,有源单点激励时圆柱壳体径向振动速度分布呈周期性变化规律。由于振动波在壳体上的叠加作用,使不同频率和方向上振动速度变化规律不同,且激励点处的振动幅值不一定最大。随着结构阻尼的增大,激励点处振动速度级增大;且激励频率越高,其他位置振动速度级随结构阻尼增大而整体降低程度越大。这主要是由于结构阻尼越大,圆柱壳体振动能量损耗越大;且随着激励频率提高,振动速度传播衰减越快。因此,结构阻尼的存在使反射波作用效果减弱,进而提高激励点处的振动速度,使振动能量向激励点处集中,且结构阻尼越大和频率越高,这种能量集中效应越显著。

图2 单点激励时壳体径向振动速度Fig.2 Radial vibration velocity of cylindrical shell with single point excitation
从图3可知,在圆柱壳体声辐射近场,受表面波作用,声压衰减较快,其沿圆柱壳体的空间分布规律与振动速度分布规律相近,且声压随结构阻尼的变化规律也与振动速度变化规律相近;在圆柱壳体声辐射远场,声压衰减较慢,近似为球面波衰减规律,且声压表现为圆柱壳体各位置振动的综合作用效果,从而使远场声压随结构阻尼变化规律与近场变化规律不同。比较图3不同激励力幅值计算结果可知,由于激励力幅值增大,圆柱壳体辐射功率增加,从而使辐射声压增大,且在辐射方向近场和远场的声压增加值近似相等。

图3 单点激励时壳体径向辐射声压Fig.3 Radial radiated acoustic pressure of cylindrical shell with single point excitation
从图4可知,单点激励时圆柱壳体横切面与纵切面声辐射远场具有一定指向性,声压分布具有周期性特征。在圆柱壳体横切面声辐射远场,随着频率提高,声辐射功率增大,但声压变化较大,声辐射波束分瓣增多,远场指向性加强,且激励力作用方向辐射声压最大;在圆柱壳体纵切面声辐射远场,随着激励频率提高,其声辐射变化特征与横切面声辐射远场变化特征相近。
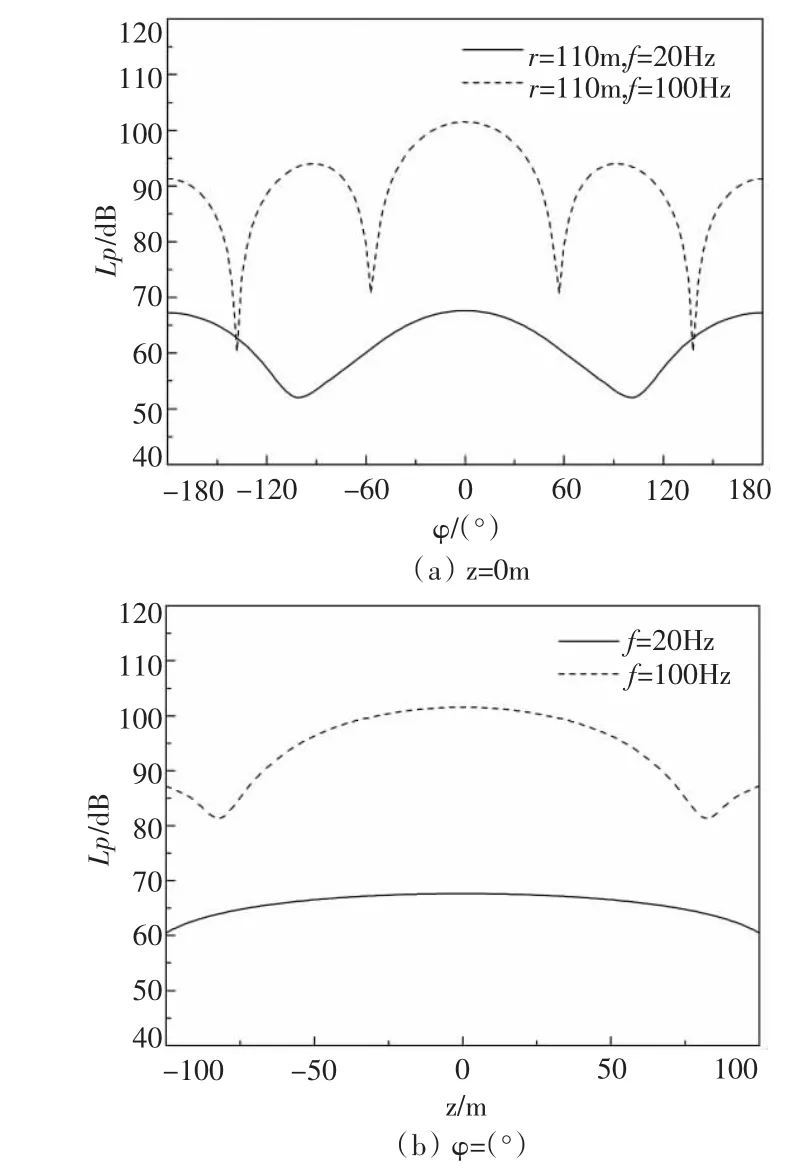
图4 单点激励时壳体远场声辐射特性Fig.4 Far field characteristics of acoustic radiation with single point excitation
2.2 有源多点激励
设多点激励时径向力作用点分别为(0,0,a)、(- z0,0,a)、(z0,0,a),其中z0=3 m,则由式(8)和式(11)可得多点激励模态力的计算式:

将式 (13)代入壳体振动速度与辐射声压计算式,可计算出多点激励时径向振动速度与辐射声压,结果如图5~图7所示。
比较图2与图5可知,多点激励时壳体径向振动速度分布规律与单点激励时不同,多点激励时壳体振动为各单点激励时壳体振动相互作用结果,振动能量增加,且振动能量表现为向力作用点处集中趋势。比较图3与图6可知,由于多点激励时声辐射为各单点激励时声辐射的叠加作用,从而使近场辐射声压变化规律与单点激励时有所不同,但其空间分布规律与振动分布规律相近。在声辐射远场,声压衰减规律与单点激励时相同,近似为球面波衰减规律,且频率越高,辐射声压越大。

图5 多点激励时壳体径向振动速度Fig.5 Radial vibration velocity of cylindrical shell with multi-point excitation

图6 多点激励时壳体径向辐射声压Fig.6 Radial radiated acoustic pressure of cylindrical shell with multi-point excitation
从图7可知,在圆柱壳体横切面或纵切面声辐射远场,各横切面或纵切面辐射声压变化规律相近。与图4比较可知,多点激励与单点激励时的远场声压变化规律相近,在激励力对称中心方向声压最大,其它方向声压相对较小,且由于振动能量增加,多点激励时辐射声压增大,为各点激励的耦合作用结果。通过比较有限长圆柱壳体单点激励与多点激励辐射声场特性可知,激励力作用方向为声辐射能量主要集中方向,而当各激励点间的距离较小时,可用单点激励条件近似模拟多点激励的声辐射远场。

图7 多点激励时壳体远场声辐射特性Fig.7 Far field characteristics of acoustic radiation with multi-point excitation
3 结语
利用圆柱壳体耦合振动理论,推导了有源点激励时水中有限长圆柱壳体振动速度与辐射声压计算式,获得了有源点激励时水中有限长圆柱壳体振动速度分布特征、声辐射近场和远场特性。随着阻尼和频率的提高,水中有限长圆柱壳体振动与声辐射能量向激励作用方向集中,且不同频率或不同辐射方向,其声压变化规律不同。在声辐射近场,声压衰减较快,声压分布规律与壳体振动分布规律相近;在声辐射远场,声压衰减近似为球面波衰减规律,声压分布具有一定指向性,且结构阻尼越大或频率越高,远场指向性越强。
[1]JUNGER M C,FEIT D.Sound,structures,and their interaction[M].2nd ed.Cambridge:The MIT Press,1986.
[2]STEPANISHEN P R.Modal coupling in the vibration of fluid-loaded cylindrical shells[J].J.Acoust.Soc.Am.,1982,71(4):813 -823.
[3]SANDMAN B E.Fluid-loading influence coefficients for a finite cylindrical shell[J].J.Acoust.Soc.Am.,1976,60(6):1256-1264.
[4]LAULAGNET B,GUYADER J L.Modal analysis of a shells acoustic radiation in light and heavy fluids[J].J.Sound and Vibration,1989,131(3):397 -415.
[5]GUYADER J L,LAULAGNET B.Structural acoustic radiation prediction:Expanding the vibratory response on a functional basis[J].Applied Acoustics,1994,43(3):247 -269.
[6]WANG C,LAI J C S.The sound radiation efficiency of finite length circular cylindrical shells under mechanical excitation,II:Limitations of the infinite length model[J].J.Sound and Vibration,2001,241(5):825 -838.
[7]LAULAGNET B,GUYADER J L.Sound radiation by finite cylindrical ring stiffened shells[J].J.Sound and Vibration,1990,138(2):173 -191.
[8]HARARI A,SANDMAN B E.Radiation and vibrational properties of submerged stiffened cylindrical shells[J].J.Acoust.Soc.Am.,1990,88(4):1817 -1830.
[9]汤渭霖,何兵蓉.水中有限长加肋圆柱壳体振动和声辐射近似解析解[J].声学学报,2001,26(1):1-5.
TANG Wei-lin,HE Bing-rong.Approximate analytic solution of vibration and sound radiation from stiffened finite cylindrical shells in water[J].Acta Acustica,2001,26(1):1 -5.
[10]廖长江,蒋伟康,王云,等.水中有限长纵向加肋圆柱壳体振动与声辐射[J].上海交通大学学报,2009,43(2):325-329.
[11]金广文,章林柯,缪旭弘,等.水下加肋双层圆柱壳体振动传递特性分析[J].振动与冲击,2011,30(5):218 -220.
[12]武国启.有源点激励有限长圆柱壳体辐射声场特性[J].机械工程学报,2012,48(5):76 -80.
[13]何祚镛.结构振动与声辐射[M].哈尔滨:哈尔滨工程大学出版社,2001.
Research on the radiated acoustic field characteristics of cylindrical shell with finite length in water
WU Guo-qi
(Dalian Scientific Test and Control Technology Institute,Dalian 116013,China)
The radiated acoustic field characteristics of cylindrical shell with finite length in water excited by a point source were studied theoretically.According to the cylindrical shell coupled vibration theory,the analytic expressions of radiation acoustic pressure and vibration velocity of finite cylindrical shell in water excited by a point source ane derived.Based on these formulas,the vibration velocity distribution along with cylindrical shell and acoustic radiation characteristics at near field and far field were solved and investigated.The research results show that the vibration energy and acoustic radiation energy of cylindrical shell concentrate on the excitation points with the increase of the structural damping,and this effect becomes stronger when the frequency increases.In the near field,the acoustic pressure attenuates quickly with approximate distribution as the shell vibration.In the far field,the acoustic pressure attenuation shows approximate spherical wave attenuation,and the acoustic pressure distribution has a certain direction,in which the main direction of acoustic radiation is the same as the direction of excitation.
cylindrical shell;radiated acoustics field;source excitation;structural damping;concentration effect
TB532
A
1672-7649(2014)01-0046-06
10.3404/j.issn.1672-7649.2014.01.010
2011-09-26;
2013-02-04
装备预先研究资助项目(51310040202)
武国启(1979-),男,博士,工程师,主要从事舰船振动噪声测试分析。
- 舰船科学技术的其它文章
- 磁流变阻尼器在船舶减振中的应用

