考虑售后服务与回收加工的复杂设备部件生产库存控制模型

钟敬武

（76327部队，湖南郴州423026）

考虑售后服务与回收加工的复杂设备部件生产库存控制模型

钟敬武

（76327部队，湖南郴州423026）

综合考虑了大型复杂设备生产厂家各种类型的部件来源与需求，构建了复杂设备部件生产库存控制模型。模型以费用作为目标，通过权衡生产成本、库存成本以及缺货成本，从而确定合理的部件生产库存控制策略。

复杂设备部件；生产库存；售后服务；回收加工；控制模型

生产厂家与客户需要确定稳定的关系，这种关系不仅仅局限于设备的采购，而且需要在设备的整个全寿命周期中密切地合作。当今社会产品实现模块化生产与装配，产品基本上由若干部件组成，复杂设备各部件工艺复杂，生产周期相对较长，所以生产厂家必须持有一些部件库存，以快速响应客户设备整机订货装配设备和设备部件单独订货的需求。同时厂家需要承担售后服务协议规定的设备维修保障的内容，所以生产厂家的部件库存也需要满足设备售后服务的需求。复杂设备重要性程度高，停机会造成巨大的损失。设备发生故障时，一般进行换件维修，以减少停机时间。更换下来的故障件仍有较大的利用价值，生产厂家往往将对替换下的故障件进行回收与重加工，以节约资源，降低生产成本[1-2]。图1给出了生产库存系统的运行框架结构，不难发现，生产库存需要满足3个方面的部件需求：即设备订货、部件单独订货与售后服务的部件需求。同时部件库存不仅仅来源传统意义的新部件生产，也来源于故障件的修复与重加工[3]。如何制定设备部件生产库存控制计划，满足各方面的部件需求且不因为库存积压而造成经济损失，这是当今复杂设备生产厂家面临的一个难题。

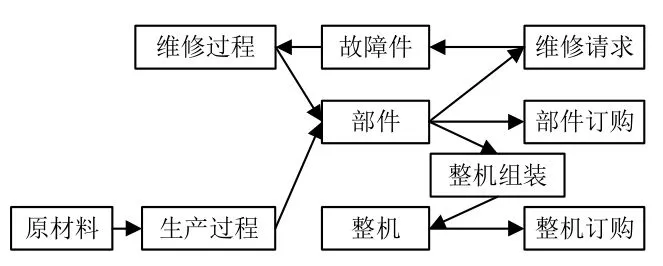
图1 生产库存系统运行框架Fig.1 Production inventory system operating framework

在生产库存方面，Smith[4]较早地关注生产库存，提出了带有下降需求的物品最优生产批量策略。Cheng[5]进一步将Smith模型扩展到生产变质性物品的情形。Wee和Wang[6]提出了允许短缺的生产库存控制模型，考虑带有常数变质率的物品以及一般时变需求。Yan和Cheng[7]通过假定生产以及变质率可随时间任意变化而进一步研究了连续生产的生产库存问题。Pan[8]和Ouyang[9]等考虑了需求不确定且提前期可控下的生产库存联合决策。Zhou[10]等在假定时变需求与部分短缺量延期供给的前提下，提出了一种寻求易变质物品在有限计划期内的最优生产与订购策略的生产调整模型。Mondal B[11]和Mondal S[12]等研究了有缺陷的产品的生产库存。从当前的文献来看，它们主要考虑生产成品整机订货的情况而没有考虑部件订货的情况，仅仅将产品需求考虑为单一的客户订货，而并没有考虑设备保修消耗部件的情况，库存来源仅仅考虑了新部件的生产，忽略了故障件的回收加工。本文将综合考虑复杂设备各种类型的部件来源与需求，构建复杂设备生产库存控制模型。

1 问题描述与基本假设

本文的研究对象为一个需要面对设备订货部件需求、部件独立订货需求以及售后服务部件需求的生产库存系统。目的在于建立一个部件生产库存控制模型，确定部件生产库存点以及生产时长，在满足设备订货、部件单独订货与售后服务的部件需求前提尽量地降低生产成本与库存成本，提高厂家效益。该生产库存系统符号描述如下：系统运行在有限的计划期内，H表示计划期的长度；设备订单关于时间的函数为f(t)；部件i订单关于时间的函数为si(t)；部件i维修需求函数为λi(t)；记Ii(t)为部件i在t时刻的库存水平；Pi为部件i的常数生产率；di为部件i所需的生产提前期，即部件i开始加工到成品入库的时间；Ri为回收加工周期；ni为部件i的机用数；采用(Ii0,Di)对生产库存进行控制，Ii0为部件i的生产点库存，Di为部件i的持续生产时长，即当库存降为Ii0时，连续生产长为Di的一段时间，Di包括生产提前期以及实际生产期；K为有限计划期内的生产库存控制周期数；Tik为部件i第k个周期开始时刻（i=1,2,…,I），Ti1=0；tik为部件i第k个生产库存控制周期生产停止时刻；当存在部件缺货时为部件i第k个生产库存控制周期内缺货的发生时刻为部件i第k个生产库存控制周期内缺货的结束时刻；Ai为部件i的单个生产库存控制周期的固定生产成本；w表示设备的销售价格；wi表示部件i的单位销售价格；hi表示单位时间内部件i的单位库存费用；c表示设备的生产成本；ci表示部件i的单位生产成本；。

为了便于模型的建立，本文引入如下假定：

1）生产部件到达的时间段库存函数为增函数，对于任意t∈[Tik+di,Tik+Di]，

生产部件未到达的时间段库存函数为减函数，对于任意t∈[Tik,Tik+di]⋃(Tik+Di,Tik+1]，

2）故障件以一定比例报废，其余部件可以进行重加工，且重加工后与新产品完全一样。θi表示部件i的回收加工利用概率。

3）系统允许缺货，缺货期间造成设备订单数与部件订单数的流失数量与当前时刻订单到来的数量和系统中等待的顾客数的乘积是正比关系损失分别表示部件i缺货期间设备与部件的缺货订单损失比例系数。

4）第1类部件需求延误损失、第2类部件需求延误损失、第3类部件需求延误损失与延误的数量和时间成正比关系分别表示部件i的第1类部件需求、第2类部件需求、第3类部件需求单位产品单位时间的缺货损失费用。第1类部件需求、第2类部件需求、第3类部件需求分别表示设备订货、部件单独订货与售后服务的部件需求。

2 模型与求解

系统呈周期运行，每个周期有生产提前期，生产期以及生产间隙期3个阶段，在生产提前期与生产间隙期均无部件到达，这2个阶段库存函数为减函数，所以部件i第k个生产周期的库存最低点将在Tik+di时刻出现，记

式中，ui(η)=λi(η)-θiλi(η-Ri)+nif(η)+si(η)，为η时刻的部件i的需求率。如果，代表库存控制策略下第k个生产库存控制周期内部件i将不会发生缺货，即将不会出现，各类部件需求均能满足。如果，代表该库存控制策略下第k个生产库存控制周期内部件i将会发生缺货。考虑第k个生产库存控制周期内部件i将不会发生缺货的情况，则部件i各时段的库存Ii(t)有：

求解式（2）可以得出：

考虑第k个生产库存控制周期内部件i将发生缺货的情况，则部件i各时段的库存Ii(t)有：

记HCik为第k个生产库存控制周期的库存费用，当第k个生产库存控制周期内部件i不会发生缺货时，则有：

当第k个生产库存控制周期内部件i发生缺货时，则有：

部件缺货损失可以分为客户延误损失与客户流失损失，客户延误损失是指生产厂家对客户订货或者送修的延期反应所付出的代价，客户流失损失是指因为缺货造成客户订单流失的损失。记为第k个生产库存控制周期的客户延误损失，则有：

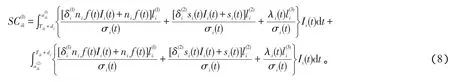
记Q″ik第k个生产库存控制周期因为部件i缺货而流失的设备订货量，则有

记q″ik为第k个生产库存控制周期流失的部件i单独订货量，则有

记SCik为第k个生产库存控制周期部件i缺货损失，则有

将部件缺货引起的设备或者部件订单流失所造成的损失看作支付的费用，记TCik为第k个生产库存控制周期部件i的期望费用，则有

生产厂家一段时间内各类部件的需求是一定的，增加部件库存可以减少缺货损失的同时也增加了库存费用。部件非连续生产模式下要尽量减少生产次数，因为每次生产需要一定与生产数量无关的固定成本，每次生产数量越多，单件产品所承担的固定成本将会越低，但是库存成本将会增加，所以需要权衡库存，生产批量之间的各种关系。记Q′k为第k个生产库存控制周期的设备订货需求，则有

记q′ik为第k个生产库存控制周期部件i的单独订货需求，则有

记第k个生产库存控制周期的设备与部件销售量分别为Qk、qik，则有第k个生产库存控制周期的利润为：

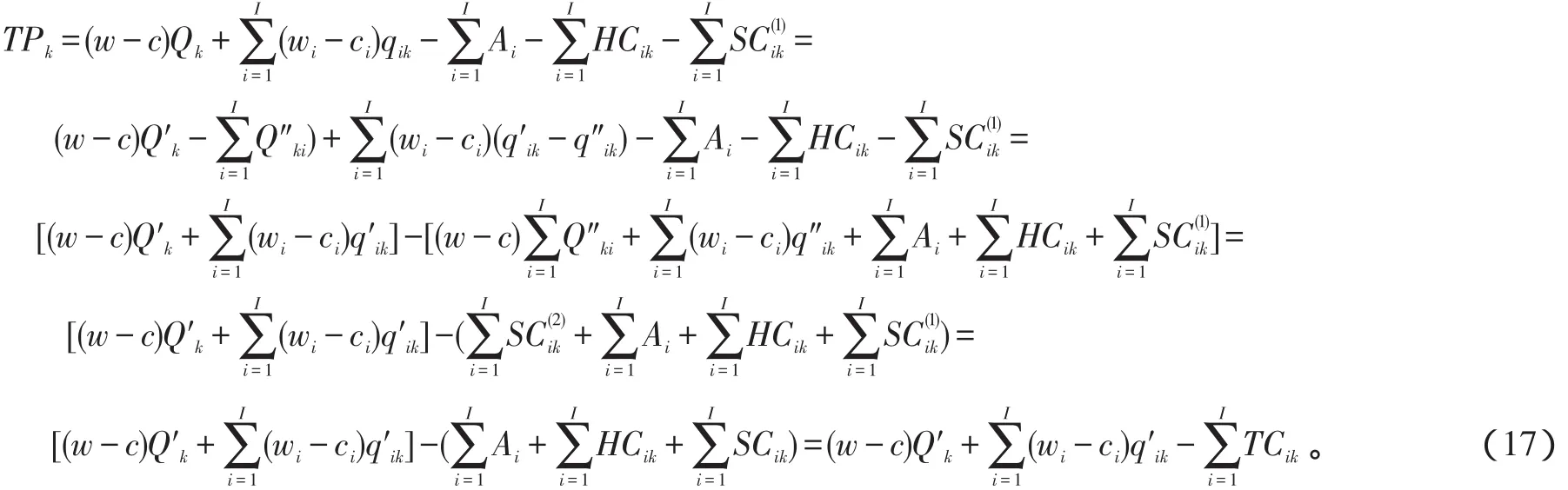
记TPK为K个生产库存控制周期的总收益为

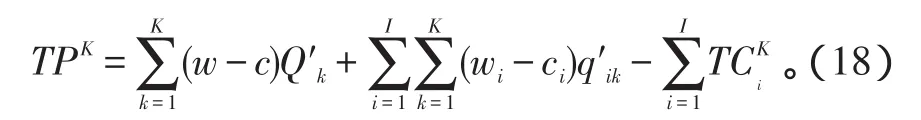
由于在不同的生产库存控制策略下，计划期H不可能正好是生产库存控制周期的整数倍，如果存在TiK＜H≤TiK+1，则可以用[0,TiK+1]时间内的平均生产库存控制效果等价于H时间段内的平均生产库存控制效果。生产计划期H时间段内的总收益可以表示为

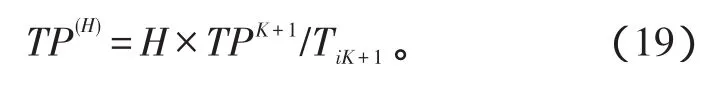
生产计划期H内部件i的期望费用可以表示为

通过调整生产点库存Ii0与周期生产时长Di，可以调整生产计划期H内的库存状态；通过求解该非线性规划问题，可以得到最优的Ii0与Di取值，从而得到最优的生产库存控制方案。该模型是一个两变量非线性规划模型。生产点库存Ii0必须为整数，因而求解该模型可以先计算出Ii0的取值范围，然后分别计算每个可行Ii0的最优生产时长Di，最后取期望费用最小的一组(Ii0,Di)。记生产计划期H内部件i不出现部件缺货所需要的最小库存为，记表示不小于x的最小整数则有：

3 应用实例

假设某复杂设备生产厂家需要制定该设备部件i的生产库存控制策略，部件i的相关参数如下：H=800h，f(t)=0.1+0.000 1t件/h，λi(t)=0.5件/h，si(t)=0.8+0.0003t件/h，Pi=5件/h，ni=1，di=20 h，Ri=5 h，Ti1=0，Ai=10千元，w=300千元/台，c=180千元/台，wi=2千元/件，ci=1千元/件

利用上文的方法可以求得Ii0和Di取不同值时的期望费用Ci，通过迭代优化，Ii0=24件，Di=30.6h为最优解，此时Ci=31.338千元，部件i生产计划期内的总费用最少。Ii0=24件时部件i生产库存控制周期生产时长Di与期望费用Ci关系如图2所示，图3给出了Ii0=24件、Di=30.6h时的生产库存控制策略下部件的库存变化情况。由图3可见，Ii0=24件、Di=30.6h时的生产库存控制策略可以取得较好的效益，有效地减少生产库存系统费用。

图2 Ii0=24时部件i周期生产时长与期望费用的关系Fig.2 Relation between production period of parti and its expected cost whenIi0=24

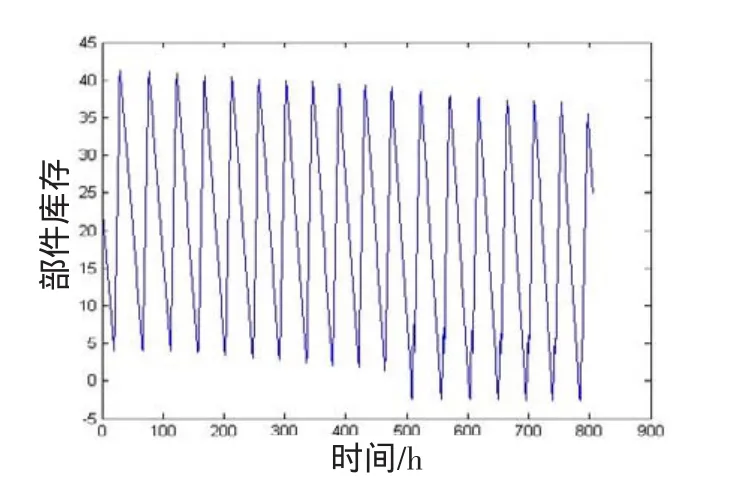
图3 (Ii0=24,Di=30.6)策略下部件i的库存变化图Fig.3 Inventory variation figure of parti when performing policy(Ii0=24,Di=30.6)

4 结束语

传统的生产库存控制理论仅仅考虑产品整机订货产生的部件需求，并没有考虑到产品部件单独订货需求；仅考虑客户订货需求，并没有考虑产品售后服务产生的部件需求。传统的生产库存理论将新产品生产作为库存的唯一来源，并没有考虑到产品的回收加工。本文通过分析复杂设备全寿命运行的特点，综合考虑部件库存的各类来源与需求，提出了考虑售后服务与回收加工的复杂设备部件生产库存控制模型，该模型通过控制生产点库存与部件生产库存控制周期生产时长对部件库存实施控制。该模型对复杂设备生产厂家的生产库存控制决策有较大的参考价值。

[1]TEUNTER R H，VLACHOS D.On the necessity of a disposal option for returned items that can be remanufactured [J].International Journal of Production Economics，2002，75（3）：257-266.

[2]NENES G.，PANAGIOTIDOU S，DEKKER R.Inventory control policies for inspection and remanufacturing of returns：A case study[J].International Journal of Production Economics，2010，125（2）：300-312.

[3]KLEBER R，ZANONI S，ZAVANELLA L.On how buyback and remanufacturing strategies affect the profitability of spare parts supply chains[J].International Journal of Production Economics，2011，133（1）：135-142.

[4]SMITH P H.Optimal production policy for linear demand [J].European Journal of Operational Research，1976，1（6）：365-367.

[5]CHENG T C E.Optimal production policy for decaying items with decreasing demand[J].European Journal of Operational Research，1989，43（2）：168-173.

[6]WEE H M，WANG W T.A variable production scheduling policy for deteriorating items with time-varying demand[J].Computer and Operations Research，1999，26（3）：237-254.

[7]YAN H，CHENG T C E.Optimal production stopping and restarting times for an EOQ model with deteriorating items[J].Journal of the Operations Research Society，1998，49（12）：1288-1295.

[8]PAN J C，YANG J S.A study of an integrated inventory with controllable lead time[J].International Journal of Production Economics，2002，40（5）：1263-1273.

[9]OUYANG L Y，WU K S，HO C H.Integrated vendorbuyer cooperative models with stochastic demand in controllable lead time[J].International Journal of Production Economics，2004，92（3）：255-266.

[10]ZHOU Y W，LAU H S，YANG S L.A new variable production scheduling strategy for deteriorating items with time-varying demand and partial lost sale[J].Computer and Operations Research，2003，30（12）：1753-1776.

[11]MONDAL B，BHUNIA A K，MAITI M.Inventory models for defective items incorporating marketing decisions with variable production cost[J].Applied Mathematical Modelling，2009，33（6）：2845-2852.

[12]MANDAL S，MAITY K，MONDAL S，et al.Optimal production inventory policy for defective items with fuzzy time period[J].Applied Mathematical Modelling，2010，34（3）：810-822.

Production Inventory Control Model of Complex Equipments Parts Concerned with After Service and Recycle Machining

ZHONG Jing-wu
（The 76327thUnit of PLA,Chenzhou Hunan 423026,China）

In this paper with the comprehensive consideration of the parts sources and demands of all kinds,a production in⁃ventory model for complex equipments parts was put forward.This model aimed to determine a reasonable parts production inventory control plan through weighing production cost,the inventory cost and shortage cost.

complex equipment parts;production inventory;after service;recycle machining;control model

TP13；F253.4

A

1673-1522（2014）05-0481-05

10.7682/j.issn.1673-1522.2014.05.017

2014-05-20；

2014-07-18

钟敬武（1974-），男，工程师，硕士。