多径信道下OFDM系统的采样频率偏移盲估计方法

李兵兵， 孙 珺， 刘明骞

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)是多载波调制技术中的一种，不仅具有很好的抗多径、抗窄带干扰性能，还大大提高了系统的频谱利用率，是现代通信技术的研究热点．然而，由于收发两端的晶振不完全匹配及移动通信系统中多普勒频移的影响，在通信系统的收发两端不可避免地存在采样频率偏移．尤其在非合作通信中，作为一种非授权接入通信模式，采样频率对于接收端是未知的，经前期的过采样率估计之后，必定还存在一定的采样频率偏移．这种偏移会破坏正交频分复用系统子载波之间的正交性，并产生时变的定时偏差，使得信号经傅里叶变换后产生载波间干扰和时变的相位变化．目前的正交频分复用系统采样频率偏移估计方法主要分为两类:数据辅助法和非数据辅助法．由于非合作通信中数据辅助法不适用，因此，笔者主要研究非数据辅助的正交频分复用系统采样频率偏移估计方法．

近年来，已有学者对非合作通信中正交频分复用系统的采样频率偏移估计方法进行了研究，但这些方法需要发射端配合[1-2]或在频偏估计之后[3]，或者不适用于多径衰落信道[4]，并且这些研究主要利用冗余的循环前缀(Cyclic Prefix，CP)与对应数据之间的相关性[5-7]，导致这些方法受信道和噪声影响较大．Liu等[2]通过对各子载波加权以及对接收信号相关函数的虚部进行变换，得到了一种非数据辅助的采样频率同步方法，但该方法需要发射端配合，且要求信道冲击响应在各子载波位置上能量相等．Ai等[3]提出一种基于保护间隔的时域估计方法，并相应地加入一自适应模块，提高了系统的实时性，但该方法用到的循环前缀长度要大于最大多经时延，且需要先估计频偏．王磊等[4]将单载波中的Gardner位同步方法应用于正交频分复用系统中，但受信道影响较大，且性能不佳．Castillo-Sanchez等[5]在采用循环前缀和正交频分复用符号尾部数据的相关进行符号定时及载波频率联合同步方法的基础上，利用定时估计值的偏移来估计采样频率偏移．胡登鹏等[6-7]在此方法上有所改进，加大了估计范围，但该方法必须先估计信噪比，且受信道和噪声影响较大．Zahedi-Ghasabeh等[8-9]提出一种基于循环平稳的谱分析方法估计采样频率偏移，但是需要知道发射端导频信息，若直接提取会受到采样频率偏移带来的衰减和多径衰落信道影响，并且频偏对其性能也有一定影响．

针对上述问题，笔者提出一种基于循环特性的正交频分复用系统采样频率偏移盲估计方法，可实现非合作通信系统中多径衰落环境下正交频分复用系统采样偏移估计．该方法首先利用一种改进的循环谱进行计算，在全局范围内，以大步长搜索最大值位置，并将此作为谱相关点粗估计值;然后利用另一种改进的循环谱进行计算，在粗估计值邻域范围内，以小步长搜索最大值位置作为谱相关点;最后通过计算相关点上循环谱相位值和跳变转化以及最小二乘直线拟合后得出相位变化率，从而可以得到正交频分复用系统采样偏移的估计值．

1 非合作通信中正交频分复用系统模型

非合作通信中正交频分复用系统发射接收模型如图1所示．

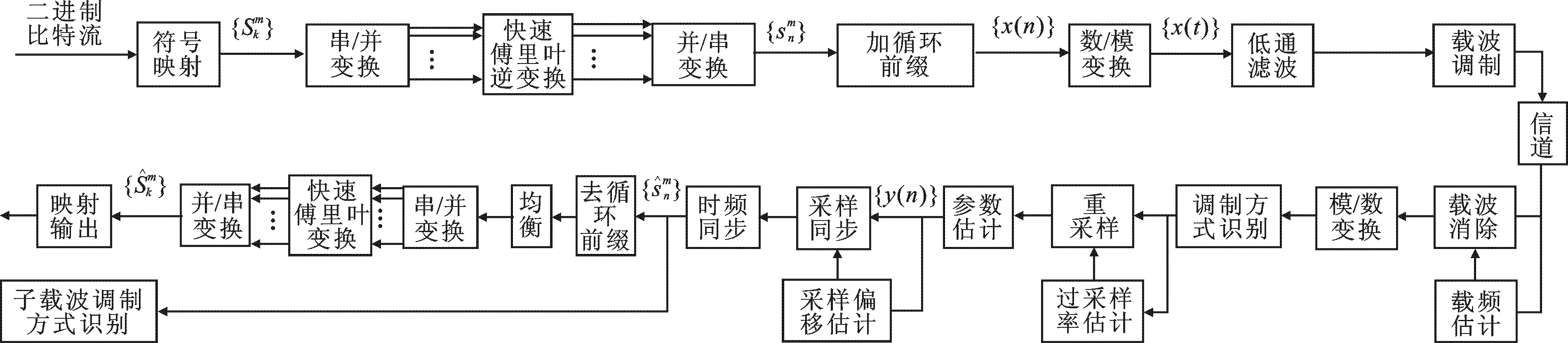
图1 非合作通信中正交频分复用系统发射接收模型

设正交频分复用信号有N个子载波，则第m个符号经过反傅里叶变换后输出的正交频分复用信号可表示为

(1)

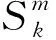
(2)

经数/模变换，得第m+1个符号处的输出值x(m，t)为

(3)

其中，gT(t)是宽度为T=(N+Nc)Ts的矩形脉冲波形，Ts为发送符号的采样间隔，T为符号周期，则连续的输出值x(t)表达式为

(4)

2 采样频率偏移盲估计方法

2.1 多径信道下正交频分复用系统的采样频率偏移的影响

对输出x(t)进行截取和傅里叶变换，代入式(4)可得

(5)

其中，G(f)为g(t)的傅里叶变换．x(t)再经过低通滤波、载波调制、信道、载波消除等环节后，在接收到的信号中存在噪声、信道与滤波影响和载波频率偏移，将信道与滤波影响统一当成信道影响，其表达式可表示为

(6)

式中，αlexp(jφl)和tl分别是第l径上的信道响应和接收时延，P为径数，h(t)表示多径信道的时域冲击响应，fo为载波频率偏移，n(t)表示加性高斯白噪声．对y(t)进行傅里叶变换后，可得

Y(f)=X(f-fo)H(f-fo)+N(f) ,

(7)

其中，Y(f)、X(f)、H(f)和N(f)分别为接收信号、发射信号、信道响应和加性高斯白噪声的傅里叶变换．

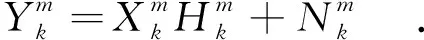
(8)

(9)

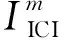
(10)

由此可见，这种偏移会带来时变的相位变化和载波间干扰，破坏正交频分复用系统子载波之间的正交性．

2.2 多径信道下正交频分复用系统的采样频率偏移盲估计方法

利用循环谱对正交频分复用信号进行检测，已广泛用于实际通信中[10]．笔者将相关导频在循环谱中对应位置设为相关点位置，这在非合作通信系统中是未知的，因此研究的关键在于相关导频在循环谱中对应位置(即相关点位置)的提取．

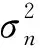
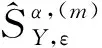
将式(12)代入循环谱计算表达式，可得

(13)

令[α0，f0]为相关点位置，即f0+α0/2和f0-α0/2位置处的导频之间具有相关性，可以得到

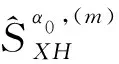
其值基本不变．再令

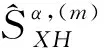
则当取f=(1+ε)(f0+εf)，α=(1+ε)α0时，代入式(12)，可得

对循环谱计算式进行了一种改进，得到如下表达式:

(15)

其中，k为差值．为减小其他位置的相关性，以便于提取，k一般要取大于1的数．为尽量利用所得数据，这里取k=2，则

(16)

当α=α0，f=f0时，

根据中心极限定理，v、vH、vH2均可近似认为是均值为零的高斯白噪声．

当α≠α0或f≠f0时，

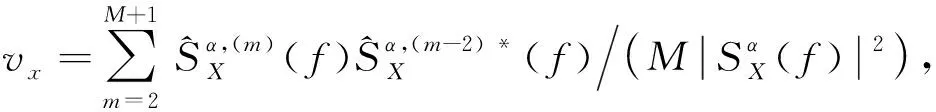
(19)

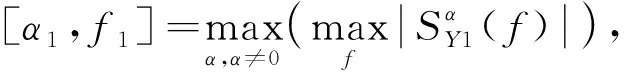
为了减少噪声影响，对循环谱计算式又进行了另一种改进，得到如下表达式:

(20)

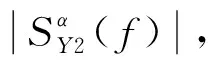
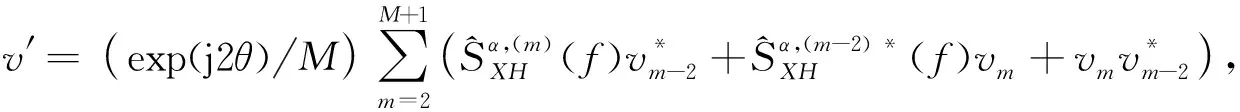
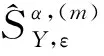
(22)

其中，θ=2πεLα/(N(1+ε))，为相位偏移系数．在相位相关点处，即当f= (1+ε)(f0+εf)，α= (1+ε)α0时，

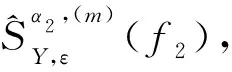
为提高采样频率偏移估计的精度，这里对1～M个符号相关点循环谱的相位值进行计算．当ε=0.000 2 时，对窗口为20个符号长度进行循环谱计算，取其相位Sn作图2(a)．从图2(a)中可看出，由于Sn∈ (-π，π]，在边界点处会发生相位跳变．为提高采样频率偏移估计的精度和范围，需要将Sn转化为全范围内相位Sa．笔者提出用以下方法进行跳变转化，使其变为一条直线，如图4(b)所示，以便进行进一步计算：根据Sn前后差值为正号的个数判断采样频率偏移估计符号为fa(fa值取1或 -1)，Sn乘以fa；从1到M，将an作为相位值变化因子，设定an初始值为 -π，将Sn(m)转化为(an，an+2π] 范围内相位Sa(m)．当Sa(m)≥an+π 时，an=an+π/2，计算Sa(m+1)，以此类推．完成后，对所得Sa进行最小二乘直线拟合，求其斜率ka．再根据下式估算采样频率偏移值ε:

ε=fa/(2πLα2/(Nka)-1) ．

(24)

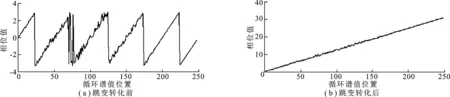
图2 相关点循环谱相位图

图3 在不同采样频率偏移值下的性能图

3 仿真结果及分析

为了验证上述方法的有效性，通过MATLAB仿真软件进行仿真实验，其所使用的仿真条件为：载波个数N=64 个，1/4循环前缀(CP)长度，符号周期Ts=10 μs，采样频率为 8 MHz，具有一对相关导频的正交频分复用信号作为信号源，信道为SU13径信道、TU 6径信道和指数衰落9径信道，蒙特卡罗仿真次数为 1 000 次．

图3是在指数衰落9径信道以及相同相对频率偏移和定时误差情况下，不同采样频率偏移值时的性能图．从图3中可以看出，笔者提出的方法在采样频率偏移值较大时也具有较好的性能，只是频率偏移值越小，估计精度越高．根据式(22)和式(24)可知，笔者提出的方法采样频率偏移估计范围与窗口长度L、子载波个数N、相关导频间隔α等有关，必须满足θ= 2πεLα/(N(1+ε))∈ (-π，π]条件．

图4是采样频率偏移ε为1×10-3、相对频率偏移εf为4.25、定时误差Te为20个符号，在3种不同信道条件下笔者提出的方法与现有的数据相关方法的性能对比图．图4表明，在相同条件下，笔者提出的方法相对于数据相关方法，均方误差更小，估计精度有显著提高．此外，笔者提出的方法的估计性能在信噪比为 [-5 dB，0 dB] 时随着信噪比的增加而提高；当信噪比大于 0 dB 时，笔者提出的方法的均方误差(Mean Square Error，MSE)曲线趋于稳定；在3种不同信道下，笔者提出的方法均方误差曲线十分接近，说明信道对方法影响不大，对于信道具有良好的稳健性．

图4 笔者提出的方法与传统方法性能对比图图5 在不同相对频率偏移和定时误差条件下的性能对比图

图5是在相同采样频率偏移和多径信道下，不同相对频率偏移和定时误差条件下的性能对比图．仿真结果表明，笔者提出的方法相对于文献[9]中的方法，估计精度有所提高，尤其在低信噪比条件下．从图5中还可以看出，在较低性噪比时，笔者提出的方法就已趋于稳定，且在不同相对频率偏移和有无定时误差情况下，笔者提出的方法的均方误差(MSE)曲线均十分接近，说明相对频率偏移和定时误差对方法性能影响不大，即表明笔者提出的方法可在时频同步之前进行，适用于实际的非合作通信系统．

4 结 束 语

基于循环谱中相关点位置的循环特性，笔者提出了一种多径衰落信道下的正交频分复用系统的采样频率偏移盲估计方法．该方法可用于时频同步之前的采样同步，不需要发射端配合于其他的先验信息，降低了多径衰落和噪声的影响，提高了低信噪比时系统采样频率偏移估计的精度，并具有良好的稳健性．

[1] Laourine A, Stéphenne A, Affes S. Blind Sampling Clock Offset Estimation in OFDM System Based on Second Order Statistics [C]//Proceedings of the 40th Asilomar Conference on Signals, Systems and Computers. Piscataway: IEEE, 2006: 1782-1785.

[2] Liu G, Li B B, Pang H L. Blind Sampling Clock Offset Estimation Algorithm for OFDM System[C]//Proceedings of the 2009 2nd International Congress on Image and Signal Processing. Piscataway: IEEE, 2009: 1-4.

[3] Ai B, Shen Y, Zhong Z D, et al. Enhanced Sampling Clock Offset Correction Based on Time Domain Estimation Scheme[J]. IEEE Transactions on Consumer Electronics, 2011, 57(2): 696-704.

[4] 王磊, 徐大专. Gardner算法在OFDM 采样率同步中的应用[J]. 电子与信息学报, 2011, 33(4): 864-868.

Wang Lei, Xu Dazhuan. The Application of Gardner algorithm to Sampling Rate Synchronization in OFDM Systems[J]. Journal of Electronics & Information Technology, 2011, 33(4): 864-868.

[5] Castillo-Sanchez E, Lopéz-Martinez F J, Martos-Naya E, et al. Joint time, Frequency and Sampling Clock Synchronization for OFDM-based Systems[C]//Wireless Communications and Networking Conference. New York: IEEE, 2009: 491776.

[6] 胡登鹏, 张尔扬. 非数据辅助的OFDM系统采样频率同步算法[J]. 信号处理, 2010, 26(6): 956-960.

Hu Dengpeng, Zhang Eryang. Non-data-aided Sampling Frequency Synchronization Algorithm for OFDM Systems[J]. Signal Processing, 2010, 26(6): 956-960.

[7] 胡登鹏. OFDM系统中的非数据辅助同步及PAPR抑制技术研究[D]. 湖南: 国防科学技术大学, 2010.

[8] Zahedi-Ghasabeh A, Tarighat A, Daneshrad B. Sampling Clock Frequency Offset Compensation for Feature Detection in Spectrum Sensing[C]//IEEE International Conference on Communications. Piscataway: IEEE Press, 2010: 5501997.

[9] Zahedi-Ghasabeh A, Tarighat A, Daneshrad B. Spectrum Sensing of OFDM Waveforms Using Embedded Pilots in the Presence of Impairments[J]. IEEE Transactions on Vehicular Technology, 2012, 61(3): 1208-1221.

[10] Socheleau F X, Houcke S, Ciblat P, et al. Cognitive OFDM System Detection Using Pilot Tones Second and Third-order Cyclostationarity[J]. Signal Processing, 2011, 91(2): 252-268.