地基微波辐射计自定标的改进算法

李江漫， 郭立新， 林乐科， 赵振维，舒婷婷， 陈后财

(1. 西安电子科技大学 物理与光电工程学院，陕西 西安 710071；2. 中国电波传播研究所 电波环境特性及模化技术重点实验室，山东 青岛 266107)

微波辐射计有很多种类型，如全功率型、迪克型、双参考温度自动增益补偿型、数字增益自动补偿型等[1]．微波辐射计的定标是指标定输出电压与输入噪声温度之间定量关系的过程[2]．定标是利用微波辐射计测量的重要前提，定标精度的高低直接影响微波辐射计对大气亮温的测量，进而影响其对环境参数的遥感[3-7]．

微波辐射计的定标大体上可分为两种方法：分步定标法，即分别完成接收机的定标和天线的定标；整体定标法，即从天线到最终输出的整体定标．分步定标法需要测量的中间参数较多， 因此误差来源多，定标精度低．整体定标一次完成，没有中间环节，因此定标精度较高．在定标中往往需要用到两个稳定的、不同温度的噪声源，常常将黑体作为高温噪声源，将液氮作为低温噪声源．使用液氮定标虽然精确，但缺点是液氮价格贵，且输运、放置不方便．

笔者根据原始的自定标方法，推导出适用于地基微波辐射计的普遍自定标形式，并且针对水平不均匀大气，提出一种改进的自定标方法，即原始自定标之后，在不同仰角的定标值附近搜索最佳补偿误差，使回归曲线逼近原点，相关系数接近1，从而修正由水平不均匀大气带来的误差，提高定标精度．利用中国电波传播研究所自主研制的双通道微波辐射计进行自定标实验，并与探空的仿真结果进行对比，验证了此方法的有效性．

1 原始自定标原理及步骤

1.1 亮温与大气衰减的相互转换

计算大气亮温的基本公式为

(1)

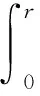
大气的等效辐射温度定义为

(2)

其中，Tm可以通过其与地面的温度和相对湿度的统计关系得到．

由式(1)和(2)可得

Tsky=2.73 exp(-τ(0, ∞))+Tm[1-exp(-τ(0, ∞))] ,

(3)

由式(3)推出大气衰减的表达式为

τ(0, ∞)=ln((Tm-2.73)/(Tm-Tsky)) ．

(4)

1.2 不同天顶角下的大气衰减与天顶角的关系

垂直高度为z，天顶角为0°的大气衰减为

(5)

对于水平均匀的大气，垂直高度为z，斜路径长度为r，天顶角为θ的大气衰减为

由式(7)看出，在大气水平均匀时，不同天顶角下的大气衰减与天顶角的正割值成线性关系，其延长线经过原点，且斜率等于天顶角为0时的大气衰减．因此在定标时可以先用不同天顶角的亮温初值来计算对应天顶角下的大气衰减，然后对大气衰减和天顶角的正割值进行线性回归，再用回归出的直线的斜率替换初始的天顶方向的大气衰减值，由此天顶衰减转换为天顶亮温，经过不断迭代循环，最终收敛并且得到较为准确的定标系数．

1.3 自定标的步骤

在已知参考黑体亮温和对应电压的前提下，原始自定标提供的地基微波辐射计的亮温传递函数为[8]

Tsky=Tref+G(Vsky-Vref)fw,

(8)

式中，Tref是参考黑体的亮温，Vref是对应的反射镜指向参考黑体时的电压．Tsky是大气亮温，Vsky是反射镜指向大气时的电压，fw是与覆盖辐射计镜面的泡沫材料的发射率有关的常数，G是定标增益，且

G=Tnd/(Vref+nd-Vref) ,

(9)

式中，Vref+nd是辐射计反射镜指向参考黑体并加上噪声二极管时的电压，Tnd是噪声温度，虽然比较稳定，但是会随着环境的变化产生很小的变动，是需要确定的定标系数．于是在已知第1个噪声源——参考黑体亮温的前提下，只需要再计算出第2个噪声源——天顶亮温就可以求解出准确的定标系数Tnd．

把自定标的过程归纳为5步[8]:

(1) 给定标系数Tnd设置一个初始值，代入式(8)求出各个天顶角下的亮温:

(2) 将各个天顶角下的亮温和等效辐射温度(等效辐射温度可以通过其与地面的温度和相对湿度的统计关系得到)代入式(4)，求出各个天顶角下的大气衰减:

(3) 对大气衰减与天顶角的正割值进行线性回归，令天顶方向的大气衰减τ(0,∞)(0°)等于其斜率;

(4) 将天顶方向大气衰减τ(0,∞)(0°)和天顶方向等效辐射温度代入式(3)，计算出天顶亮温:

(5) 将天顶亮温Tsky(0°)代入式(8)，求解出新的Tnd值:

结束之后将Tnd回代到步骤(1)中，进行下一次循环，不断地更新Tnd，直至其收敛，把此时的Tnd作为准确的定标系数，自定标完成．

2 改进的自定标方法

2.1 普遍自定标公式推导

基于接收机的输出电压与输入噪声温度之间呈线性关系的地基微波辐射计，把原始自定标中的亮温传递函数改写为T=a+bV的形式，

Tsky=Tref+G(Vsky-Vref)fw=Tref-GfwVref+GfwVsky=a+bVsky,

(10)

式中，a=Tref-GfwVref，b=Gfw．在已知参考黑体的亮温和对应的电压的前提下，可得出a和b的关系:

这样就可以把a或b(a、b之间可以互相转换)当做定标系数，以a为例进行自定标．步骤(1)改写为:给定标系数a设置一个初始值，代入亮温传递函数求出各个天顶角下的亮温:

Tsky(θ)=a+bVsky(θ)=a+((Tref-a)/Vref)Vsky(θ) ,

(13)

步骤(5)改写为：根据

由天顶亮温Tsky(0°)求解出新的a值:

a=Tref-Vref((Tsky(0°)-Tref)/(Vsky(0°)-Vref)) ,

(16)

其他步骤不变．将a值回代到步骤(1)中，进行下一次循环，不断地更新a，直至其收敛，把此时的a作为准确的定标系数，自定标完成．

2.2 搜索最佳补偿误差

在大气水平不均匀的情况下，利用原始自定标方法，回归曲线可能会偏离原点，相关系数偏离1，此时会产生较大定标误差．原始自定标之后，在不同的天顶角亮温附近，搜索最佳补偿误差，以回归曲线的截距小于 0.000 1 和相关系数大于0.999作为截止条件，可以修正原始自定标，提高定标精度．如图1，利用100组仿真数据进行两种定标方法的对比．可以看出，由于大气的水平不均匀性，造成原始自定标的误差不稳定 (0～ 3.5 K)，而改进的搜索自定标由于在原始自定标的基础上进行了修正，定标误差可以减小到 1 K 以下．为避免出现多个最佳补偿值，搜索范围被限制在 -2 K 到 2 K．地基微波辐射计在实际对空工作过程中，难免受到大气中云的影响，如果在此搜索范围内不能达到截止条件，说明此时大气的水平不均匀性较为明显，则改进的自定标方法失效，不宜采用．

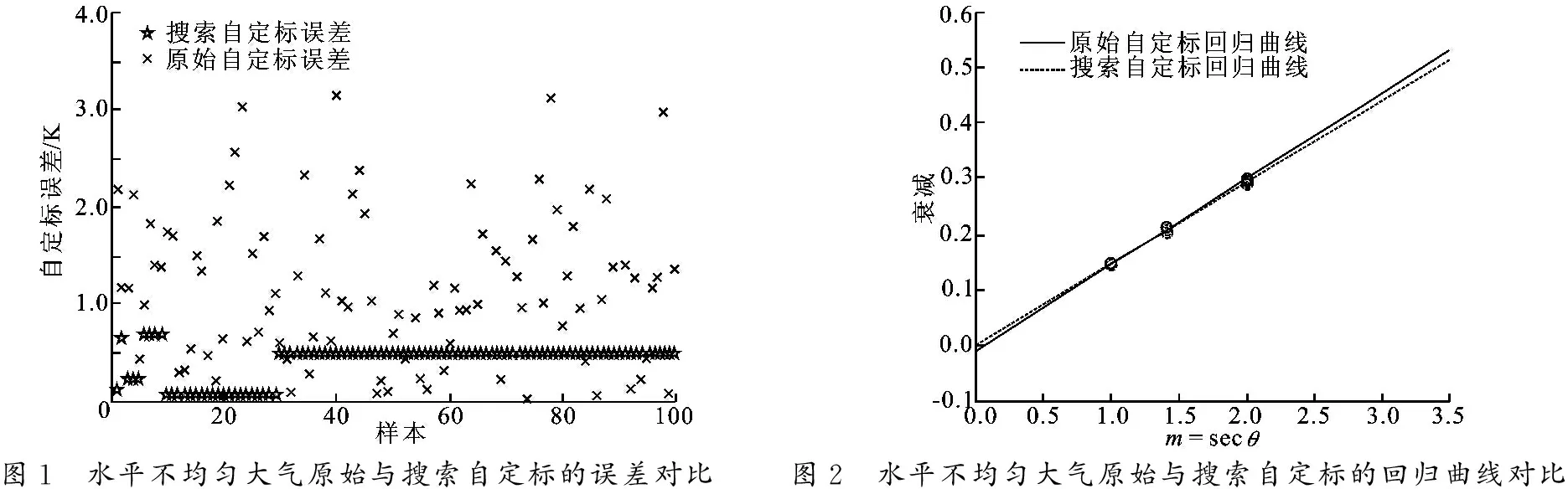
图1 水平不均匀大气原始与搜索自定标的误差对比图2 水平不均匀大气原始与搜索自定标的回归曲线对比

图2为原始自定标与改进的搜索自定标的典型个例，图中“○”代表根据辐射计观测亮温计算得到的不同天顶角下的大气衰减．原始自定标回归曲线的截距为 -0.010 7，偏离原点，相关系数为 0.997 0，而搜索自定标将其修正到接近原点，截距为 3.022×10-5，相关系数为 0.999 3，并使天顶亮温的定标误差由 2.31 K 下降到 0.92 K．

图3 水平均匀大气原始与搜索自定标的误差对比

在大气水平均匀的情况下，利用原始自定标方法，回归曲线几乎经过原点，相关系数接近于1，定标误差主要来源于等效辐射温度的计算误差，且对定标精度的影响很小．搜索自定标仍然能够减小等效辐射温度带来的误差．如图3，利用100组仿真数据进行两种定标方法的对比．可以看出，在大气水平均匀的情况下，原始自定标的误差较小 (0～ 0.3 K)，改进的搜索自定标由于在原始自定标的基础上进行了修正，使定标误差又有所减小．

3 实验验证

将改进的自定标方法应用到中国电波传播研究所自主研制的双通道微波辐射计中，此辐射计属于实时定标微波辐射计，中心频率为 23.8 GHz 和 31.65 GHz，其原理可参考文献[1]．把微波辐射计输出方程写为T=a+bV的形式,

T和V分别为辐射计天线接收到的亮温和对应的电压．为了准确地测量大气辐射，需要保证微波辐射计具有良好的线性度，此种微波辐射计输出方程通过采用电压的差值，既消除了本机噪声变化的影响，又消除了增益变化的影响，具有良好的稳定性和线性度，有利于微波遥感的使用．利用两种自定标方法对定标系数a进行校准．

下面说明实验情况．将双通道微波辐射计置于楼顶四周空旷的地方，自定标时在0°方位角(正北)选取的天顶角为0°、45°、60°，为了补偿仪器水平误差，又在180°方位角增加了两个相等的天顶角：45°、60°．

表1是2011年12月10日双通道微波辐射计自定标后的实测亮温与某地探空的仿真亮温的比较，表中括号内的数字表示观测时间．可以看出，经过改进自定标的修正，定标误差有所降低．

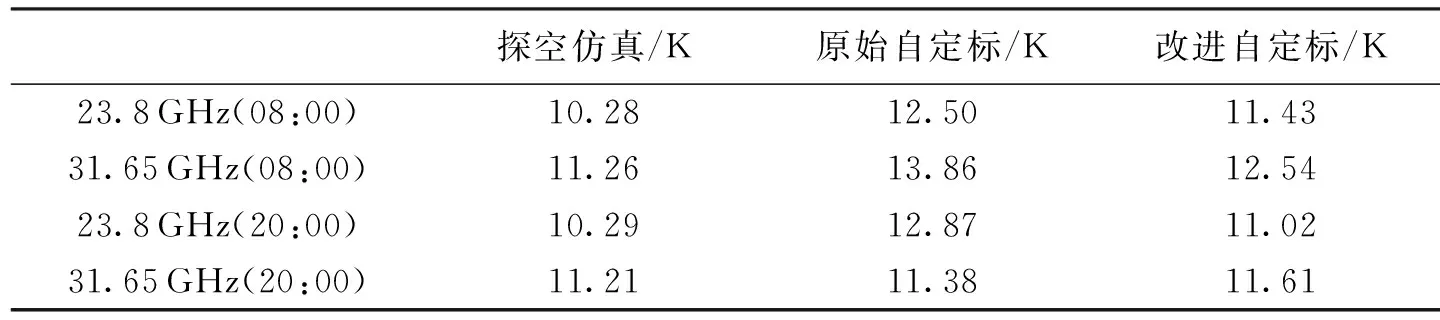
表1 2011年12月10日定标亮温与仿真亮温的比较

4 结 束 语

笔者由原始的自定标公式推导出了适用于地基微波辐射计的普遍自定标形式和定标流程，并针对水平不均匀大气原始自定标误差较大的问题，提出了改进的地基微波辐射计的自定标方法；在原始自定标之后，对其结果进行修正，提高了定标精度．

值得注意的是，以上改进的自定标方法仅适用于水汽密度和温度水平不均匀的情形，在大气存在液水较多的情况下，水平和温度不均匀性非常明显，此方法不适用．如何解决液水不均匀性带来的定标误差将是下一步要研究的问题，可以考虑针对观测路径中云的液水总量，对液水的辐射进行估计，并在观测亮温中加以修正，从而实现阴天的自定标．

[1] 李靖, 张俊荣, 赵凯. 实时定标微波辐射计[J]. 电子科学学刊, 1998, 20(2): 285-288.

Li Jing, Zhang Junrong, Zhao Kai. Real-time Calibrated Microwave Radiometer[J]. Journal of Electronics, 1998, 20(2): 285-288.

[2] 李靖, 姜景山, 李茂堂. 微波辐射计定标[J]. 遥感技术与应用, 1999, 14(1): 1-4.

Li Jing, Jiang Jingshan, Li Maotang. Calibration of Microwave Radiometer[J]. Remote Sensing Technology and Application, 1999, 14(1): 1-4.

[3] Helder D, Thome K J, Mishra N, et al. Absolute Radiometric Calibration of Landsat Using a Pseudo Invariant Calibration Site[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1360-1369.

[4] Helder D L, Karki S, Bhatt R, et al. Radiometric Calibration of the Landsat Mss Sensor Series[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(6): 2380-2399.

[5] Huang F, Huang Y, Flynn L E, et al. Radiometric Calibration of the Solar Backscatter Ultraviolet Sounder and Validation of Ozone Profile Retrievasl[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(12): 4956-4964.

[6] McCorkel J, Thome K, Lockwood R B. Absolute Radiometric Calibration of Narrow-swath Imaging Sensors with Reference to Non-coincident Wide-swath Sensors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1309-1318.

[7] De Wachter E, Haefele A, Kämpfer N, et al. The Seoul Water Vapor Radiometer for the Middle Atmosphere: Calibration, Retrieval, and Validation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(3): 1052-1062.

[8] Liljegren J C. Automatic Self-Calibration of ARM Microwave Radiometers[C]//Microwave Radiometry and Remote Sensing of the Earth’s Surface and Atmosphere. New York: ACM, 2000: 433-441.

[9] Han Y. Analysis and Improvement of Tipping Calibration for Ground-based Microwave Radiometers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(3): 1260-1276.

[10] D’orazio A, De Sario M, Gramegna T, et al. Optimisation of Tipping Curve Calibration of Microwave Radiometer[J]. Electronics Letters, 2003, 39(12): 905-906.