广义预测控制在非线性系统中的应用研究

王丽飞，刘洪娥，于佐军（中国石油大学，山东 青岛 266555）

1 引言

广义预测控制是Clarke等人在1987年针对工业过程的特点，在保持最小方差自校正控制的在线辨识、最小方差控制的基础上，吸取了DMC和MAC中的滚动优化策略，提出的一种新型的计算机控制。广义预测控制具有诸多优点：首先，它是基于参数模型的，而其他的预测控制算法大部分是基于非参数模型的。其次，它保留了自适应控制的优点，而且较自适应控制有更好的鲁棒性。最后，由于采用多步预测、滚动优化和反馈校正等策略，其控制效果更适应工业过程控制的要求[1～3]。由于这些优点，广义预测控制一出现就受到了控制界和工业界的广泛关注，其理论研究不断深入，并在很多工业过程中得到应用，取得了较好的控制效果[4]。

但是，目前广义预测控制的研究对象大部分是线性离散时间系统，对非线性系统广义预测控制的研究，由于难于构造被控对象的多步预报模型因而导致广义预测控制律求解困难。目前非线性系统的广义预测控制一般都是用神经网络的方法来获得被控对象的多步预测值，这种方法需要首先训练神经网络，其模型不能进行在线辨识[5～7]。本文针对一类比较具有普遍意义的非线性系统，首先将其转化为时变参数的线性系统，然后使用具有遗忘因子的最小二乘法或是多项式逼近法在线辨识模型参数，进行广义预测控制。并以二容液位系统为模型，进行了仿真研究，取得了较好的控制效果。

2 非线性系统的广义预测控制

2.1 非线性系统模型及其等效时变线性系统

非线性系统被控对象的输入输出模型可以描述如下：

其中 u、 y分别表示系统的输入、输出，m、n分别表示输入输出阶次，ε(t)表示噪声干扰， f(•)是未知的关于y(t −1),y(t−n),u(t−1),u(t−m)的非线性函数，并且满足下列条件：

（1） 0)0,0,0( =f

（2） f (•)关于y(t −1),y(t−n),u(t−1),u(t−m)连续可导，且各偏导数有界。

条件（1）要求系统的平衡点为零点，若不满足此条件，可通过坐标变化使之满足此条件，条件（2）代表了一类非线性系统，也是许多实际非线性系统过程所满足的。这两个条件并不是很苛刻，对这类非线性系统的研究也具有实际意义。可以证明[8～9]，满足以上两个条件的非线性系统可以等价地表示为如下的时变线性系统：

并且 ai（i = 1,2,n ）、bj（ j = 1,2,n） 是有界的。这一时变线性系统相当于将非线性系统等价为一个由无数线性系统组成的线性模型的集合，每一时刻对应集合中的某个线性模型。

根据以上论述，我们就可以在广义预测控制的每一步，先辨识非线性系统的线性化模型，然后再进一步求解广义预测控制律。

2.2 模型参数的辨识

式（2）是由一个非线性系统等价而来的参数未知的时变线性系统，当非线性系统不是处在稳定工作点时，其等价的时变线性系统的参数是不断变化的，因此，要对系统进行控制，就必须先辨识系统模型的参数（在系统的阶次已知的情况下），要辨识的模型如下：

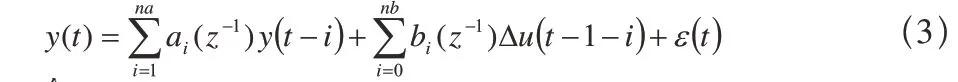
令：

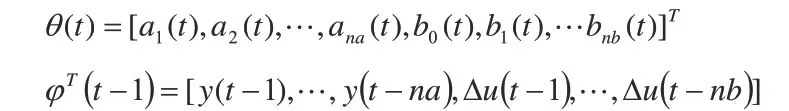
则式(3)可表示为：

对于以上时变系统模型的辨识，如果参数属于慢时变的，可以采用改进的线性定常系统的辨识方法，本文采用具有遗忘因子的最小二乘法，其计算公式如下：

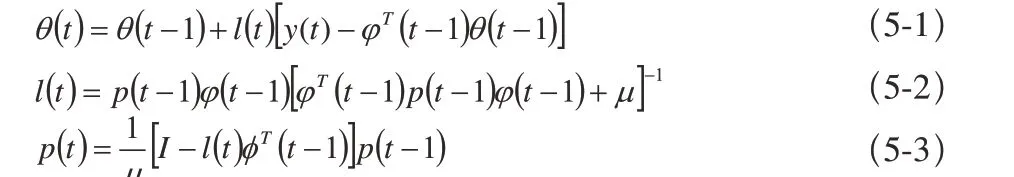
其中， 0 <µ ≤1是遗忘因子，一般可取 0 . 95<µ ≤1， l (k )为权因子， p ( k )为正定的协方差阵。θ 与p的初值可用一次完成的最小二乘法得到，或直接选为

如果时变参数变化较慢，采用上述具有遗忘因子的最小二乘法就能获得较好的效果，但在参数变化较快的情况下，参数的辨识应该依据对应时刻的观察数据，不能过多地使用过去时刻的观测数据，因此很难满足时变参数辨识时对观察数据充分丰富的要求，使用上述算法就存在较大的误差，为了解决该问题，比较常用的是多项式逼近法。所谓多项式逼近方法，就是将时变序列展开成多项式基函数的线性组合形式，通过辨识这些线性组合的定常系数来实现时变参数的辨识。

对于式(3)中 )(tθ 的任意一个元素，在任意一个时间间隔 ],[21ttt ∈ 上，存在多项式：

通过引入如下一个变量代换[10～11]

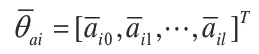
则式(3)可以写成：

)(tξ 为系统的噪声与多项式的截断项所造成的未建模动态误差之和。

对(10)进行辨识时，先进行正则化处理：

即：

对上式中的参数采用如下带有死区的最小二乘算法进行辨识：

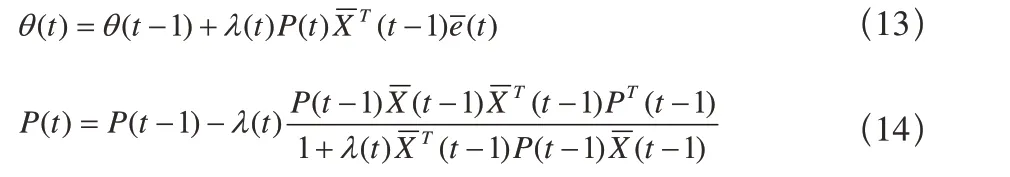
死区切换函数定义为：

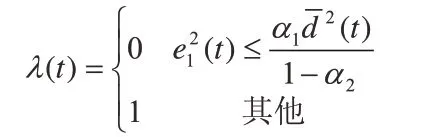
其中，α1=1+trace(P(0))， t rP (0)表示矩阵 P (t)在时刻等于 t =0时的迹，α2为小于1的任选正常数。

2.3 非线性系统工作点变化时的广义预测控制

在实际的过程中，大部分的非线性系统都是工作在某一稳定工作点上，因此，系统稳定运行时，可以将系统作为一个时不变线性系统进行控制，而当系统的工作点变化的时候，就需要采用上面所论述的原理，将非线性系统等价为时变的线性系统，在线辨识模型参数，并进行广义预测控制，使系统由一个工作点快速平稳地达到另外一个工作点。

非线性系统工作点变化时的广义预测控制的步骤：

（1）如果非线性系统工作在同一工作点，转到3，否则执行2；

（2）用具有遗忘因子的递推最小二乘法（参数变化缓慢）或多项式逼近时变参数的方法估计模型参数 )(tai， )(tbj；

（3）求解Diophantine方程，计算jE、jF、jG、jH；

（4）计算矩阵G和G ( G + λ I )−1；

（5）求解控制量 )(tu ；

（6）返回到1，继续执行；

此处需要说明的是，如果用具有遗忘因子的递推最小二乘法辨识参数，那么它与线性系统广义预测控制中的具有遗忘因子的递推最小二乘法虽然都是用来估计系统的参数，但意义并不相同，前者求的是非线性系统在不同工作点附近的线性化的模型参数，目的是使线性化后的模型能尽可能逼近非线性模型，参数变化比较大；后者求的是线性系统的模型参数，它的作用是使辨识值不断地接近线性系统模型参数的真实值，参数变化不大。此外，如果非线性系统是由一个工作点运行到令一个工作点时，辨识的初始值应该设为起始工作点线性化后的模型参数。

3 广义预测控制在二容液位系统中的应用

3.1 二容液位控制系统的建模

二容液位系统如图1所示：

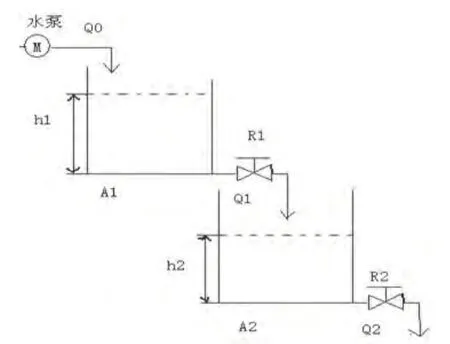
图1 二容液位图

在图1中，上面的容器称为容器1，下面的容器称为容器2。容器1的水流输入量Q0是由水泵M决定的，水泵的正常工作区间为0-3 m3/h，即水泵能够提供的最大水流为 1 /1200m3/s。容器1的水流输出量Q1与容器1的液位高度的开方成正比，即 Q1 = k 1h1，同理，容器2的水流输出量Q2与容器2的液位高度的开方成正比，即，则根据物料平衡方程：

容器内储液量的变化率 = 单位时间内液体流入量 - 单位时间内液体流出量

可以得到容器1的液位：

容器2的液位：

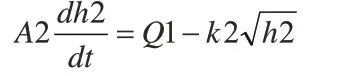
其中的A1，A2分别为容器1、容器2的横截面积。

3.2 二容液位系统的仿真

在二容液位系统的仿真研究中，以容器1的水流输入量作为输入控制量，以容器2的液位高度作为输出控制量，系统用CARMA表示，即

采用具有遗忘因子的最小二乘法辨识模型的参数。系统的仿真输出采用四阶龙格—库塔法得到，其公式如下：

其中：

f( t,y)为系统的模型。

3.3 仿真结果

系统在幅值为7.8881e-004的阶越响应下的响应曲线如图2所示：

图2 阶跃响应曲线

初始液位为0，液位设定值为0.35m，采用具有遗忘因子的最小二乘法辨识系统模型，其仿真结果如图3所示：

图3 具有遗忘因子的最小二乘法辨识系统模型的输出曲线

采用多项式逼近法辨识模型参数时，其仿真结果如图4所示：

由图3和图4可以看出，由于参数变化比较缓慢，无论是采用多项式逼近法辨识模型还是采用具有遗忘因子的最小二乘法辨识模型，输出曲线相差不大，都能实现非线性系统工作点的切换。

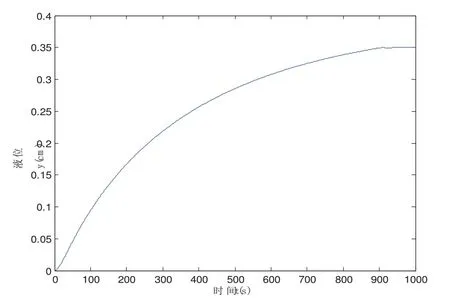
图4 多项式逼近法辨识模型的输出曲线

4 结语

本文针对一类比较具有普遍意义的非线性系统，首先将其转化为时变参数的线性系统，然后使用具有遗忘因子的最小二乘法或是多项式逼近法在线辨识模型参数，进行广义预测控制，给出了两种辨识时变参数的方法，并以二容液位系统为模型，进行了仿真研究。结果表明，使用具有遗忘因子的最小二乘法或是多项式逼近法在线辨识模型参数，输出曲线相差不大，都能实现非线性系统工作点的切换。

[1] 孙洪涛. 广义预测控制的应用研究[D]. 天津: 天津大学, 2006.

[2] 师五喜. 广义预测控制中Diophantine矩阵多项式方程的显示解[J]. 控制理论与应用. 2007, 24 (2) : 261 - 263.

[3] Xu Zuhua, Zhu Yucai, Han Kai, Zhao Jun, Qian Jixin. A multi-iteration pseudo-linear regression method and an adaptive disturbance model for MPC [J]. Journal of Process Control, 2010, 20 (4) : 384 - 395.

[4] 张月静, 徐喆. 基于广义预测控制的储罐液位系统的仿真分析[J]. 当代化工, 2013, 42 (11) : 1605 - 1607.

[5] 张敏杰. 改进广义预测控制算法的研究[D]. 太原: 太原理工大学, 2012.

[6] 李奇安, 邵明新, 李悦. 基于遗传算法的多变量增量型广义预测控制[J]. 江南大学学报 (自然科学版) , 2013, 12 (5): 626 - 630.

[7] Jiang Jian-hua, Li Xi, Deng Zhong-hua, Yang Jie, Zhang Yisheng. Thermal management of an independent steam reformer for a solid oxide fuel cell with constrained generalized predictive control[J]. International Journal of Hydrogen Energy, 2012 (37) : 12317 - 12331.

[8] 郭健, 朱瑞军, 胡维礼. 一类非线性系统的自适应广义预测控制[J]. 控制与决策. 2001, 16 (3) : 358 - 361.

[9] 李奇安, 金鑫. 对角CARIMA模型多变量广义预测近似解耦控制[J]. 浙江大学学报 (工学版) , 2013, 47 (10) : 1764 - 1769.

[10] L Guo. Estimating time varying parameters by the Kalman filter based algorithm: Stability and convergence[J].IEEE Trans on Autom Contr, 1990, 35 (2): 141 - 147.

[11] 李德权. 线性时变系统的辨识及其应用研究[D]. 南京: 东南大学, 2003.