创设有效问题情境，构建高效智慧课堂——以人教版“竖直平面内圆周运动”为例

●施坚

教学中有效的物理问题情境，是指能够激起学生的探究欲望，并能促使他们运用已有知识，通过质疑、分析或推理，去主动建构新知识的物理问题情境。 从具体操作层面来看，有效问题情境的创设要把握好以下四个特性：目的性，针对性，可行性，生成性。

在人教版必修2《竖直平面内圆周运动》中数学，笔者进行“创设有效问题情境，构建高效智慧课堂”的尝试。

一、联系生活，创设导入情境

生活中蕴藏着丰富的物理学知识，一旦教师将生活中的物理教育资源与书本上的物理学理论知识融通起来创设物理情境，引发认知冲突，激发他们探求新知的渴望，学生学习的兴趣陡然增加。

比如，在本课中，教师演示“水流星”实验引入课题：

将透明水流星杯子和细绳出示给学生看，倒入红墨水，演示若倾倒杯子红墨水流出，但若快速在竖直平面内旋转，红墨水始终未曾流出。请学生注意观察现象，并暗示学生来挑战这个水流星实验，向不敢挑战的学生提问。

教师：你担心什么？

学生：担心水会流出来。

教师：水会在哪里流出来？

学生：最高点。

教师：在最高点水真的会流出来吗？

教师再请学生表演水流星，引导学生观察，发现水没有流出。

教师：这节课研究竖直平面内的圆周运动，找到水不会在最高点流出来的条件。

这样引入，运用了学生感兴趣的生活事例，通过巧妙地提问，化平常为惊奇，把深刻的物理问题自然地引出。

二、重视知识，创设求知情境

物理学中的知识都具有重要的价值和意义，它们提出或发现往往都具有一定的现实背景，可能是为了描述或解释某些物理现象，也可能是为了研究或解决某一物理问题。

比如，本课中，教师由浅入深，设置拱形桥和凹形桥两类典型模型创设求知情境，完成本节课的知识深入的前期铺垫。

教师：大家知道哪些竖直平面内的圆周运动？

学生：过山车、摩天轮、荡秋千、汽车拱形过桥等。

教师图片展示生活中竖直平面内的圆周运动。

教师： 我们先研究竖直平面内的圆周运动的一部分——汽车拱形过桥。

播放汽车快速通过拱形高坡脱离坡面酿成车祸的视屏（渗透安全教育）。

教师利用课件展示问题1：如图1 所示，若已知质量为m 的汽车以速度v 通过拱形桥最高点，拱形桥的半径为R，试求此时汽车对桥的压力的表达式。

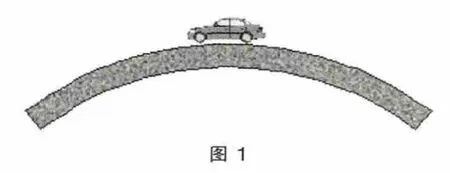
请学生推导压力的表达式，并把压力与汽车的重力比较，得出汽车处于失重状态，当速度增大时，对桥的压力减小，当速度时，对桥的压力为零，汽车处于完全失重状态，当速度时，重力不足以提供向心力，汽车做离心运动，很容易酿成车祸，让学生体会到安全过桥时速度不能过大。

教师：如果把地球看成是巨大的拱形桥，桥面的半径就是地球的半径R（约为6400km）。根据上面的分析，汽车速度越大，它对地面的压力就越小。 当压力为零时，这时驾驶员与座椅之间的压力是多少？

学生：压力为零，驾驶员处于完全失重状态。

教师：驾驶员躯体各部分之间的压力是多少？他这是有什么感觉？

学生：感觉漂浮在空中。

教师播放宇航员王亚平空中授课的视屏， 适当解说不仅是宇航员， 其实航天器内各个物体都处于完全失重状态（为下一章《万有引力与航天》的学习打下埋下伏笔）。

教师：接着我们来研究汽车过凹形桥。凹形桥又叫“过水路面”，公路在通过小型水库泄洪闸的下游时常常修建凹形桥。

教师利用课件展示问题2：如图2 所示，若已知质量为m 的汽车以速度v 通过凹形桥最低点，拱形桥的半径为R，试求此时汽车对桥的压力的表达式。

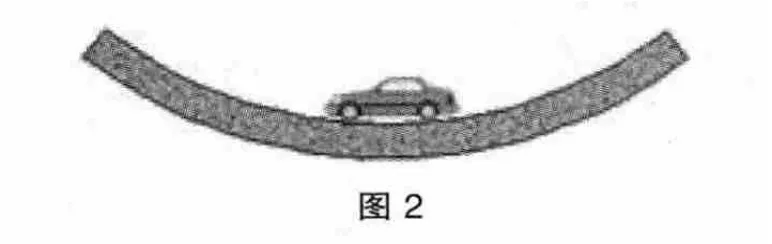
请学生推导压力的表达式，并把压力与汽车的重力比较，得出汽车处于超重状态，当速度增大时，对桥的压力越大。

教师：下面学习完整的竖直平面内圆周运动——过山车。

这样一种结合生活情境的探究式教学既符合了“知识的必要性”，又锻炼了学生的思维，敦促学生建构了有意义的新知识，符合物理学科知识发展的要求，也遵循了学生的认知规律。

三、基于实验，创设探究情境

生动活泼、内涵丰富的物理实验是创设探究情境、激发学生智慧的不二选择。

比如，本课中，教师提出过山车模型的名词后首先播放了游乐场过山车视频， 继而用5 个问题引导学生分组实验深入探究过山车模型所含物理知识和规律，实验装置如图3 所示。

用小球从斜轨某高处由静止释放模拟过山车，在学生分组实验前用课件展示问题3：实验中，小球的释放高度是否影响它完成竖直面内圆周运动？ 问题4：实验中，若小球未完成竖直面内圆周运动，你认为圆周上最难通过的位置在哪里？

让学生小组内代表回答上面的两个问题。

学生：只有当小球从足够的高处下落，小球才能完成竖直面内圆周运动，否则小球会掉下来，脱离轨道，最难通过的位置是最高点。教师用课件展示小球在光滑圆环内侧做圆周运动，如图4 所示。提出问题5：若欲使质量，m 的小球完成半径为R 的竖直面内圆周运动，起始位置是否为2R 高处，为什么？ 问题6：试分析得出小球通过最高点的最小速度vmin可以为0？ 若vmin≠0，具体有何特征，请用相关物理量表达。

教师引导学生理论分析，得出：

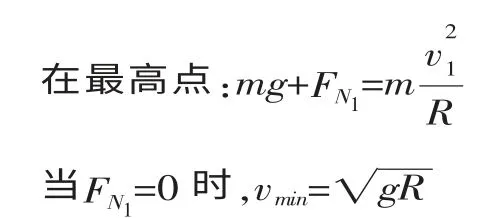
由此得出小球能过最高点条件：v≥vmin或轨道对小球的作用力FN≥0，即

教师做演示实验（装置如图5 所示），从实验来探究小球能过最高点的速度条件，其中小球刚好过圆周最高点对应的轨道释放位置由前置实验中的学生找出，并利用光电传感器测出小球通过最高点的时间t，用游标卡尺测出小球的直径d，则速度（该速度公式可在苏威尔软件中编辑，d 用具体数据代入，t 直接由传感器测得并显示，从而在软件页面直接显示速度实际值。 如图6）

而在测最高点临界速度的理论值时，首先需测量圆周轨道内径D，并在excel 软件中完成相关实验数据得录入，结合公式直接得到理论值（如图 7）。

探究的理论值和实际值在误差范围内非常接近，学生不断在实验探究和理论推导中，感受物理规律和逻辑推理挑战。将看似索然无趣的知识结论，转变成引人入胜的探究过程，激活了学生灵动的思维。正所谓，教的是思维，收获的是智慧。

教师：光滑圆环限定了小球的轨道，如果用长为L 的细绳拉着小球在竖直面内做圆周运动， 是不是在最高点也需要达到一定的临界速度？

教师请学生上来用手指甩动绳球模型， 并要求学生当小球速度比较小时， 注意观察小球的运动情况。 是否可以加以理论推导？

教师提示： 过山车模型与绳球模型的受力特征不仅在最高点相似， 在最低点和其他位置也完全相同，得出的规律可以相互借鉴。教师要求学生再次演示并体会在球速较小时小球对手指拉力的变化，请猜想或判断拉力的最小点和最大点在何处？

学生结合实验观察判断拉力的最小点在最高点，拉力的最大点在最低处。

为了让学生真切地感受拉力的两个最值点，教师再次应用实验结合理论推导来创设探究情境。

教师做演示实验（装置如图8 所示），为了便于观察，教师把细绳替换为伸缩性比较明显的橡皮筋，实验开始前，小球明显离地面有20-30 cm 的距离，当把细绳拉至水平在释放小球，可以很清晰地看到小球在最低点时把绳子拉得很长，几乎贴地而过，甚至可以听到和地面的摩擦声。此时，学生得到了充分的感性认知，拉力的最大点在最低处。 教师在此并没有得过且过，而是提醒学生，该模型其实已经不是严格意义上的圆周运动，因为圆周半径已经变化， 但实验很好地体现了最低点拉力达到最大值，但这只停留在感性层面。

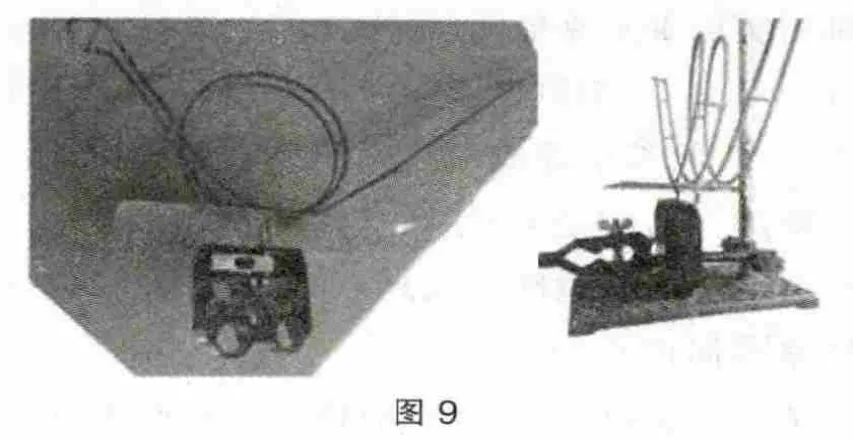
教师做演示实验（装置如图9 所示），将过山车轨道与拉力传感器改装后连为一体，当小球在轨道上运动时，传感器定量地显示了小球在最高点和最低点与轨道间的弹力。

整个流程，学生感性和理性认知都得到了深化，感受了物理学用数据说话的严谨。

四、学生参与，创设生成情境

现代课堂教学的价值取向是探究与生成并重，生成的课堂体现的是教师的主导作用、学生的主体地位，体现的是新课程理念下的教学观。

比如，本课中，教师提出杆球模型（如图10 所示）：即将杆与小球固定，拉着小球在竖直面内做圆周运动。

学生分组实验，教师用课件展示问题7：实验中，你认为小球通过竖直面内圆周最高点时最小速度vmin是多少？ 并提醒学生在实验时注意：刚开始用力使小球快速地在竖直面内转动起来后，然后手不动，让钢丝带动小球自由转动，观察小球最后一次通过最高点的现象。

各小组学生代表回答。

学生代表1：小球通过竖直面内圆周最高点最小速度应该为零。

学生代表2：最高点最小速度有时为零，有时好像不为零。

学生代表3：小球最后一次通过最高点时速度趋向零。

学生代表4：通过最高点时速度就是零。

…

教师面对学生似乎统一而又不统一的答案：“应该”、“好像”、“趋向”、“就是”，是灌输给学生“小球通过竖直面内圆周最高点时最小速度的确是零”，还是教师用实验事实来证明“最小速度的确是零”？ 教师选择的是后者，亲自把实验演示了一遍，发现在速度几乎为零时，都能完成通过圆周最高点。

教师提出问题8：实验中，你认为杆球模型与绳球模型中小球通过圆周最高点时最小速度的不同的本质原因何在？

学生：因为绳在最高点只能对小球产生拉力，而杆在最高点时对小球可以产生拉力， 也可以产生支持力。

教师提出问题9：如图11 所示，已知轻杆长为L，小球质量为m，请结合力学知识分析小球通过圆周最高点时杆对球的作用力与通过速度v 之间的关系表达式。

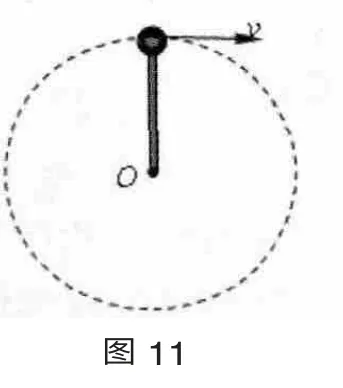
有了前面过山车、绳球模型的铺垫，杆球模型力与速度间关系的理论推导完全放开，即有学生上台板演。

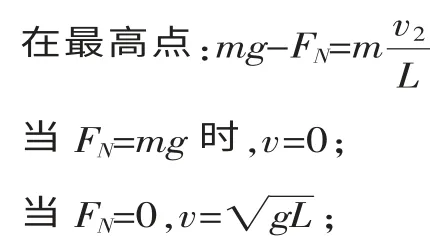
至此，杆球模型的探究学习告一段落，但学生对这一模型的印象和理解是深刻的，因为有了他们参与的身影，有他们自己内化生成了相关知识和规律。

五、激活知识，创设应用情境

在教学中创设有效的物理应用情境，激活知识，使学生运用所学的知识解决生活、社会、科技中的实际问题，感受学习知识的必要性。

比如，本课中的管球模型的展开，教师就是让学生类比杆球模型来获取。

教师：如果让小球在光滑的竖直圆管内运动，如图12 所示，与杆球模型比较，小球在受力和运动上有共同点吗？

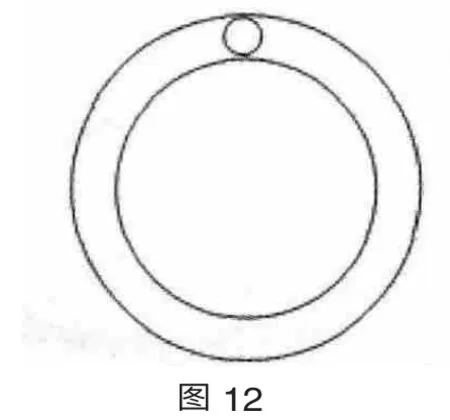
学生：因为小球在管道底部一定挤压外轨，在管道顶部可能挤压外轨，也可能挤压内轨，甚至不挤压内外轨，故完全可类比杆球模型，即当时，小球与内关壁闭挤压受到向上的弹力；当时，与管壁无弹力；当时，小球与外管壁挤压受到向下的弹力。

到此，本节课所呈现的6 个模型均已讲解，为了检验本节课学生实际收获， 教师用课件展示问题10：学习了本节课，你能否解释“水流星”表演中杯在最高点杯口朝下而水不流出的原因吗？

学生：因为水在最高点时速度杯底对水的弹力和重力提供向心力，水当然不会流出来。

通过这样一个习题情境，使学生体会到，物理知识在日常生活中有着实实在在的应用价值。

笔者认为问题情境教学的过程本身就是学生思维发展的过程，教学过程和问题情境的创设首先要符合教材知识结构的特点，同时也应符合学生的认知水平、思维习惯和思维方法，通过有效的问题情境教学使学生的知识水平和思维能力真正得到提高和发展。