基于MATLAB的三次样条插值在绳套型水位流量关系定线推流中的应用
陈 靓朱庆云王书亮
(1.江苏省秦淮河水利工程管理处,江苏南京 210001;2.江苏省水文水资源勘测局南京分局,江苏南京210008;3.江苏省水文水资源勘测局盐城分局,江苏盐城 224000)
1 概述
对于影响因素复杂的绳套型水位流量关系,人们常常难以找到一个解析表达式来表示它们之间的关系,在此情况下,常用连时序法定线,即:手工绘制水位流量关系曲线。笔者较为详细地讨论了绳套型水位流量关系的成因及其常见定线方法,在此基础上,通过实例介绍了利用三次样条插值进行绳套水位流量关系定线的方法,并编写Matlab程序由计算机代替人工完成繁琐的手工作业。同时,还对人工推算值和样条插值计算值进行了误差分析,分析表明,插值流量与人工推算流量的相对误差很小。对于处理绳套型水位流量关系,基于MATLAB的三次样条插值具有简便实用的特点。
2 绳套型水位流量关系的成因
对于不稳定的水位流量关系,其影响因素较多,而绳套型水位流量关系的形成,主要有以下三种情况:
(1)受变动回水影响。当支流测站受干流涨水的顶托;干流测站受下游支流涨水的顶托;下游水库、湖泊、海洋等水体水位的变化引起的顶托;下游渠道闸门的启闭;下游河道壅水或者因水草产生阻力时,测流断面的水面比降受到影响,将引起流量变化,使得水位流量关系点分布散乱。在受变动回水影响时,水位流量关系不仅与本站水情有关,还与下游水体的水情变化有关。随着下游水体对测站影响程度的变化,水位流量关系曲线的走向也不同,有些呈现顺时针绳套,有些呈现逆时针绳套,还有的呈现“8”字或者反“8”字形绳套。
(2)受洪水涨落影响。在洪水涨落过程中,由于洪水波传播引起的附加比降不同,使得断面上的流量和同水位稳定的流量相比产生有规律的增大或者减小。洪水上涨时,其涨率为正,则附加比降为正,其流量大于同水位的稳定流流量;落水时的涨率为负,其流量小于同水位的稳定流流量。这样,一次洪水涨落过程的水位流量关系曲线就呈现为一逆时针绳套曲线。
(3)受综合因素影响。在受到上述两种因素的综合影响时,水位流量关系也会呈现绳套关系。
3 绳套型水位流量关系的几种定线方法
绳套型水位流量关系的定线方法可以总结为:
(1)对于受变动回水影响的测站,可根据具体情况采用等落差法、定落差法、落差指数法定线推流。
(2)对于受洪水涨落影响的测站,可根据具体情况采用校正因素法、低偿河长法定线推流。
(3)对于以上两种情况,也可以采用连时序法定线推流。当影响因素复杂,难以用找到函数表达式来近似表达水位流量关系时,常常采用连时序法。
4 常用的插值方法
在大量的应用领域中,人们经常面临用一个解析函数描述数据(通常是测量值)的任务。插值与数据拟合是非常实用的数值方法,是函数逼近的重要手段。在工程生产和科学试验中,自变量x与因变量y的函数关系式有时不能直接写出,而只能得到函数在若干个点的函数值或导数值。当要求知道观测点之外的函数值时,需要估计函数值在该点的值。因此,通过已有数据信息构造出函数表达式尤为重要。
插值是和拉格朗日(Lagrange)、牛顿(Newton)、高斯(Gauss)等著名数学家的名字连在一起的,它最初来源于天体计算的需要。比如:人们得到了若干观测值,即某个星球在若干已知时刻的位置,需要计算星球在另外一些时刻的位置。所谓插值,通俗地说就是,在若干已知数值之间插入计算一些未知的函数值。
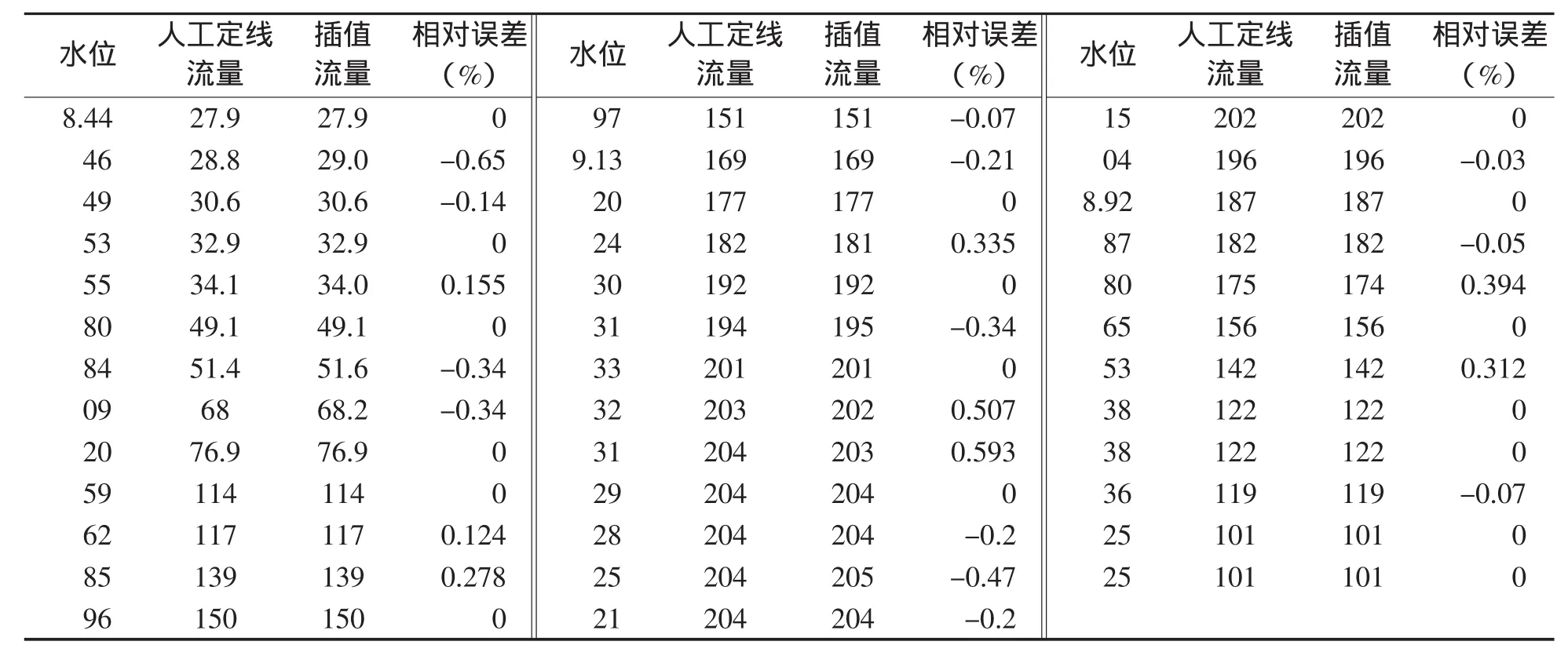
插值问题的提法是,已知n+1个节点(xj,yj)(j=0,1,…,n),其中xj互不相同,不妨设a=x0 求解的思路是,构造一个相对简单的函数y=f(x),称为插值函数,使f通过全部节点,即:f(xj)=yj(j=0,1,…,n),再用 f(x)计算插值,即:y*= f(x*)。 常用的基本插值方法包括拉格朗日多项式插值、分段线性插值和三次样条插值。 拉格朗日多项式插值中,随着节点数的增加,插值函数会出现很大的振荡,即:龙格现象;分段线性插值是将相邻的两个点用直线连接起来,其所形成的一条折线就是线性插值函数。因此,笔者只讨论三次样条插值法。 所谓样条(spline),来源于船舶、飞机等设计中描绘光滑外形曲线用的绘图工具。一根有弹性的细长木条用压铁固定在节点上,其它地方自然弯曲,如此画出的曲线称为样条曲线。人们普遍使用的样条函数是分段三次多项式。 三次样条函数的定义是:函数S(x)∈C2[a,b],且在每个小区间[xj,xj+1]上是三次多项式,其中,a=x0 图1 水位流量绳套关系曲线 (1)将绳套曲线分解为涨水支线和落水支线,分解时一般以峰顶、峰谷为分解点,把分解出的涨水、落水曲线当作单一曲线进行插值。 (2)由于受闸门控制影响,水位在上涨、下落过程出现下降或者回升时,需要分解处理为折线,这样的处理与人工绘制过程线处理方式大体一致,但人工处理时转折处会稍微圆滑一些。 (3)复杂的绳套水位流量关系曲线可以看作若干单一曲线的组合,用插值法处理时,就是把复杂的水位流量关系曲线分解为若干单一曲线之后分别插值。 (4)推求流量时,需要注意水位与单一曲线的对应。 笔者实例选取的资料是滁河晓桥水文站2010年的一次实测洪水过程,该次洪水从9月2日22∶00起涨,9月7日21∶30后落平。 由于受上游襄河口闸以及下游汊河集闸的控制,该站水位流量关系主要受变动回水影响,呈顺时针绳套,可用连时序法定线。 利用连时序定线绘制水位流量关系,受人为因素影响,绘制的绳套曲线会有差异,过程也比较繁琐。 为了解决这一问题,笔者利用三次样条插值法,编写Matlab程序,由计算机完成定线推流。 编写的Matlab程序如下: %晓桥洪水过程三次样条插值程序(可同时绘制水位面积、水位流速关系曲线) A=xlsread(′xiaoqiao2′); %sw=A(:,2), %ll=A(:,3), %mj=A(:,4), %ls=A(:,5), %subplot(2,2,1) %plot(ll,sw) %subplot(2,2,2) %plot(mj,sw) %subplot(2,2,3) %plot(ls,sw) x1=A ([2:10],2) %input stage data y1=A([2:10],3) %input discharge data x11=x1(1):0.01:x1(9), y11=interp1(x1,y1,x11,′spline′), x2=A([10:16],2) %input stage data y2=A([10:16],3) %inputdischarge data i=1:7 j=8-i xx2(i)=x2(j) yy2(i)=y2(j) x22=xx2(1):0.01:xx2(7), y22=interp1(xx2,yy2,x22,′spline′),%subplot(2,2,4) plot(y1,x1,′o′,y11,x11,y2,x2,′o′,y22,x22) 图1为Matlab程序绘制的水位流量绳套关系曲线。由图1可以看出,插值得到的曲线线条光滑,趋势合理。 表1为人工定线流量与插值流量相对误差计算表。结果表明,最大相对误差绝对值为0.65%,表中人工定线流量采用水文资料整编正式成果。 表1 人工定线流量与插值流量相对误差计算表 基于MATLAB程序的三次样条插值可以用于处理绳套水位流量关系,由计算机代替人工完成水位流量关系的定线和推流,处理方法简单实用。在本文实例中,样条插值流量与人工推算流量之间的相对误差最大值为0.65%,误差值很小,且两者之间不存在系统误差。对于复杂的绳套水位流量关系曲线,可以将其看作若干单一曲线的组合,将其分解为若干单一曲线之后分别插值,而每一条单一曲线的插值方法和本文实例完全相同。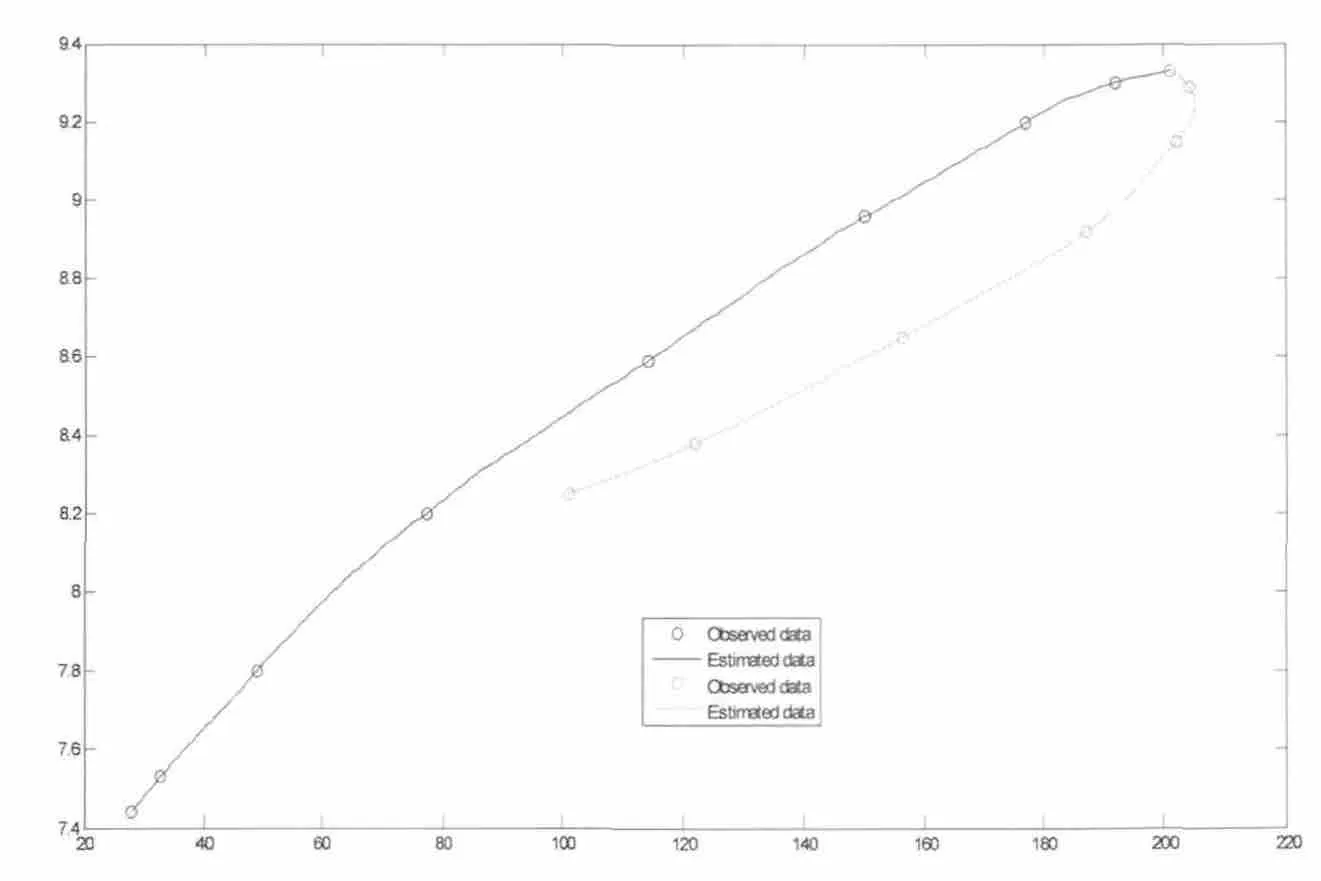
5 三次样条插值处理绳套曲线应该注意的问题
6 三次样条插值定线实例
7 误差分析
8 结语

