基于特征选择和BP神经网络的风电机组故障分类监测研究

童 超， 郭 鹏

（华北电力大学 控制与计算机工程学院，新能源电力系统国家重点实验室，北京102206）

风电机组在恶劣的自然环境下工作，极易出现故障并造成巨大的经济损失.因此，应对风电机组进行有效的实时监测和故障诊断.早期的状态监测与故障诊断技术主要是依靠仪器获取参数（如频率、振幅和速度），并与固有的参数进行比较来确定故障类型.近年来，随着计算机和信号处理技术的迅速发展，多将监测数据传输给计算机进行综合分析，得到频谱图、倒频谱图和包络线等，从而实现风电机组状态的在线监测和远程监测.也有学者通过对风电机组建模［1］来进行监测分析.同时，人工智能和机器学习方法（如神经网络、支持向量机等［2］）也被应用于风电机组状态监测中.郭鹏等［3］采用非线性状态估计技术作为建模方法，对风电机组塔架振动特性及其影响因素进行细致分析的基础上，建立了塔架振动模型，用于风电机组振动状态监测.杨宏晖等［4］提出自适应增强支持向量机集成算法，并结合风机噪声信号的人耳听觉谱特征，对风机故障进行分类识别.龙泉等［5］提出了一种基于粒子群优化反向传播神经网络（BP神经网络）的风电机组齿轮箱故障诊断方法.笔者选择结构简单、应用范围广的BP神经网络对桨距角不对称故障进行分类监测.

但是，直接采用BP神经网络对不对称故障进行分类存在以下问题：首先，由于数据采集与监视控制系统（SCADA系统）记录47个常用的风电机组参数，这些参数之间关系复杂.虽然数据越多，BP神经网络分析得到的信息会越充分、准确性越高，但是由于数据维数过高、数据过于庞大，会出现“维数灾难”的问题［6］，这势必将影响分类器的分类性能；其次，虽然多个参数可能具有很好的分类信息，但是若它们具有非常高的相关性，则将它们一起作为特征向量几乎得不到什么信息，不但增加复杂度且没有获得更多信息.因此，有必要对各个特征向量的分类能力进行评价，选择出分类能力强的特征信号，剔除冗余信息，降低特征向量的维数.目前，特征选择的研究呈现出多样化和综合性的趋势，各种新的搜索算法和评价标准都被应用到特征选择算法中［7］.杨志新等［8］提出了一种基于小波包变换与ReliefF算法的RES识别方法，用于雷达辐射源信号识别，利用ReliefF算法对雷达辐射源信号各个频段特征的分类能力进行评价，从而选择出分类能力强的信号特征组成特征向量；李宗杰等［9］采用自组织的SOM网络进行特征选择；杨飞虎［6］提出RF－MI特征选择算法和ISU－GA特征选择算法，用于网络流量识别，降低了后续分类算法的时间和空间复杂度.郭嘉［10］针对回声状态网络分类方法面向特征维数高、特征间关系复杂数据时的特征选择问题，提出了一种基于微分进化算法的封装式特征选择方法.

笔者参考上述降低特征向量维数的方法，在运用BP神经网络分类之前，选择ReliefF算法对数据进行降维处理.ReliefF算法是目前公认的性能较好的一种特征有效评估方法［8］，具有较高的运行效率且对数据集的数据类型没有限制，同时克服了Relief算法仅解决两种类别数据的分类问题和没有对数据缺失情况进行处理的缺点.

1 桨距角不对称故障分析

桨叶与发电机、轴承和齿轮箱均有直接联系，且桨叶故障的维修费用在风电场总维修费用中占较大比重，与电厂的盈利息息相关.桨叶的原始故障包括桨距角不对称（Blade angle asymmetry）和桨距角不可信（Blade angle implausibility）两大故障［11］.笔者选取桨距角不对称故障进行详细分析.

桨距角不对称故障是由桨距角不同引起的.所研究风电机组的报警系统有以下规定：在自动桨距控制模式下，2个叶片桨距角的偏差0.5°持续10s或偏差4°持续200ms，就会进行桨距角不对称报警.在高风速下，变桨距控制系统调节叶片桨距角，而在低风速时桨叶固定不动.当某一叶片桨距角与其他叶片桨距角显著不同时，就会造成停机.

图1为发生桨距角不对称故障时风机功率与桨距角的变化趋势图，在101采样点处功率下降至0，风电机组停机.图2为101采样点处3个叶片各自桨距角的放大示意图，可以发现2号叶片的桨距角明显超前于1号和3号叶片的桨距角.2号叶片的桨距角与1号叶片的桨距角之差为1.1°，大于0.5°，因此此处桨距角不对称故障引起了机组停机.

图1 桨距角不对称故障时风机功率与桨距角的变化趋势图Fig.1 Tendency chart of wind power and blade angle under asymmetrical fault conditions

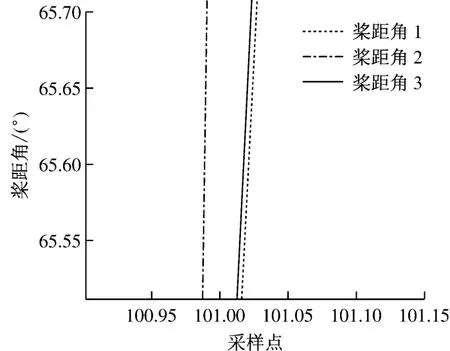
图2 在101采样点处3个叶片各自桨距角的放大示意图Fig.2 Enlarged drawing of three blade angles at sampling point 101

2 ReliefF算法变桨故障特征选择

所研究的风电机组为张家口某风电场的GE 1.5MW变桨变速机组.该机组的额定功率为1.5 MW，切入风速为3m／s，额定风速为12m／s，切出风速为25m／s.该机组的SCADA系统每隔10min记录一次各重要部件传感器的测量参数，如功率、塔架绕曲及电压等共47个参数.由于参数量较多，为了避免“维数灾难”并且去除数据的冗余性，选择ReliefF算法进行数据降维处理.

ReliefF算法的核心思想是：好的特征应使同类样本接近，使不同类样本远离.ReliefF算法首先从数据集中随机选择一个样本，然后从该样本的同类和不同类中均选择出k个最近邻样本，根据权重计算公式（1）更新每一个特征的权重.由于抽样了m次，所以上述过程迭代m次，最终得到每一个特征的平均权重.保留特征权重大于预设权值的特征，组成一个特征子集［6］.算法详细描述如下.

输入：训练数据集D、样本抽样次数m、最近邻样本个数k、特征数目n和特征权重阈值δ.

输出：特征值大于阈值δ的组成特征子集S.算法过程：

（1）初始化.置S为空集，置所有特征权重

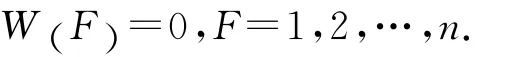
（2）从j＝1到m进行如下操作

①从D中随机选择一个样本R；

②从R的同类样本集中找出R的k个最近邻样本Hi（i＝1，2，…，k），从R 的不同类样本集中找出R的k个最近邻样本

③从F＝1到n进行如下操作

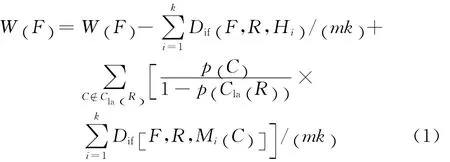
式中：p（C）表示类的分布概率；Cla（R）表示R所属的类别；Hi表示类Cla（R）中R的第i个最近邻样本；Mi（C）表示类C中R的第i个最近邻样本；Dif（F ， R1，R2）表示R1与R2在第F个特征上的差异度.

（3）从F＝1到n进行如下操作

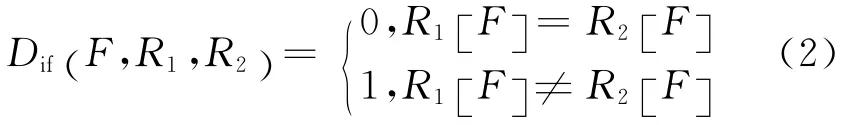
对于连续型特征

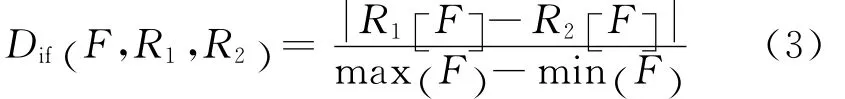
式（2）和式（3）中：R1、R2表示2个样本；R1［］F和R2［］F分别为R1和R2中第F个特征的值.

在ReliefF算法中，特征属性与类别属性的相关性越高，算法赋予的特征权重也就越高，因此可以有效地去除无关特征，但是该算法的局限在于无法去除冗余性的特征.为此，采用相关度分析将冗余的分类能力弱的特征去除.相关度计算公式如下

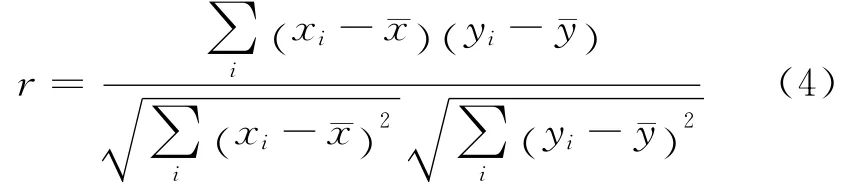
式中：xi和yi为特征值；¯x和¯y为特征均值；r为相关度.

对于给定的相关度阈值，两两分析参数的相关性，在相关性强的一对特征属性中，权重大的被保留，权重小的被去除.因此，最终保留下来的特征属性与类别属性相关性高且冗余信息小.

提取桨距角不对称故障时的数据以及部分风机正常运行时的数据，用于ReliefF算法，相关度阈值设为0.95时，计算出各个参数特征分类能力的权值，前10名示于表1.

表1 特征参数权值排名Tab.1 Weight ranking of various characteristic parameters

本研究的主要目标是建立风电机组桨距角不对称故障分类模型，桨距角不对称故障是由桨距角不同引起的，叶片桨距角偏差是桨距角不对称故障的重要衡量标准，因此应将桨距角偏差加入到最终选择的参数集中.

结合ReliefF算法所得到的结果，选择8个与桨距角不对称故障最相关的参数建立分类模型，这8个参数分别为：桨叶1桨距角偏差、桨叶2桨距角偏差、桨叶3桨距角偏差、功率因数设定值、机舱位置、塔架加速度、传动系统加速度和机舱旋转.其中，桨叶1桨距角偏差为桨叶1与桨叶2桨距角之差，桨叶2桨距角偏差为桨叶2与桨叶3桨距角之差，桨叶3桨距角偏差为桨叶3与桨叶1桨距角之差.

图3为某次发生桨距角不对称故障当天各个被选特征参数的变化趋势图，当天桨距角不对称故障发生时刻为13：03：28，对应于图中第79个采样点（即虚线所示位置）.

由图3可以看出，这8个被选特征参数在虚线附近均发生了明显的变化，其中后5个参数为ReliefF算法选择的参数，从图3可以发现这5个参数相关性低、冗余信息小，充分体现了ReliefF算法所选择的特征属性与类别属性的相关性高、特征属性间冗余信息小的特征.

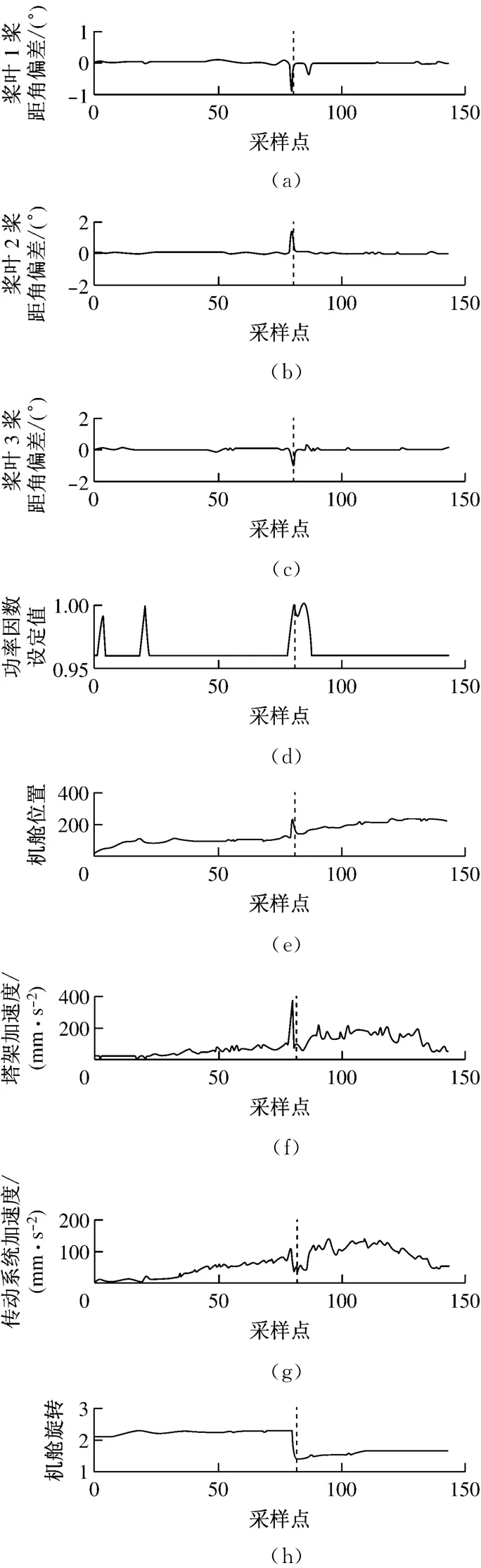
图3 某次发生桨距角不对称故障当天各个被选特征参数的变化趋势图Fig.3 Tendency chart of various characteristic parameters in the case of a certain asymmetrical fault

3 BP神经网络变桨故障分类

分类器的设计采用BP神经网络，其结构简单，是目前神经网络中应用最广的一类网络，已经成功解决了许多领域的实际问题［12］.网络结构见图4.

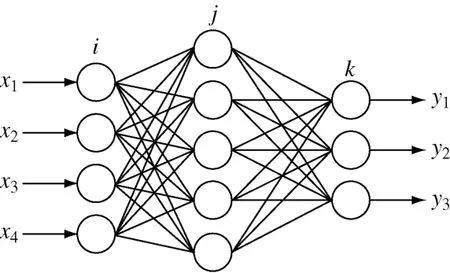
图4 BP神经网络结构Fig.4 Structure of the BP neural network

该网络由输入层、隐含层和输出层3部分组成，能够实现连续的非线性映射.BP神经网络学习过程由正向传播和误差反向传播2个过程组成.在正向传播过程中，输入层各神经元接收输入信息，并传递给隐含层各神经元；隐含层是内部信息处理层，负责信息变换，根据需求，隐含层可以设计为单隐含层或多隐含层结构；最后一个隐含层传递到输出层各神经元的信息经进一步处理后，完成一次学习的正向传播处理过程，由输出层输出信息处理结果.当实际输出与期望输出不符时，进入误差的反向传播阶段.通过网络将误差信号沿原连接通路返回，同时修改各层神经元的权值直至达到期望目标［13］.

采用第2节ReliefF算法分析得到的结论，网络输入参数为8个，即桨叶1桨距角偏差、桨叶2桨距角偏差、桨叶3桨距角偏差、功率因数设定值、机舱位置、塔架加速度、传动系统加速度和机舱旋转.采用3层BP神经网络，隐含层节点数为10，输出层节点数为1，通过输出值判断是否为桨距角不对称故障，若正常，则输出为1，若故障，则输出为0.隐含层的激活函数为Singmoid型正切函数tansig，学习效率为0.1，训练目标的误差为0.000 000 4.

整理出桨距角不对称故障18个点及正常工况342个点，组合成样本集，共360个样本，其中80%作为BP神经网络的训练样本，而剩余的20%用于检验分类的准确性.

图5显示了BP神经网络能较好地收敛于给定的相对误差，其中最佳验证性能为0.024 194，出现在第8次迭代时.图6给出了BP神经网络预测分类与实际类别的对比.由图6可知，在72个验证数据中，70个数据分类正确，2个数据分类错误，分类的准确率为97.22%，准确性较高.

图5 BP神经网络算法性能图Fig.5 Performance of the BP neural network

在分类算法中，支持向量机（SVM）算法也是较常用的方法.利用与BP神经网络相同的训练集构建SVM分类器，并采用相同的测试数据进行分类测试，结果示于图7.由图7可知，在72个验证数据中，68个数据分类正确，4个数据分类错误，分类准确率为94.44%.

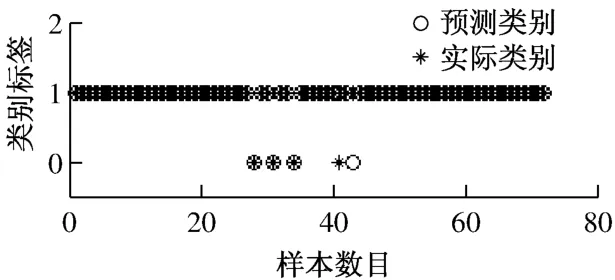
图6 BP神经网络预测分类与实际类别的对比Fig.6 Comparison between BP neural network prediction and actual classification

图7 SVM算法预测分类与实际类别的对比Fig.7 Comparison between SVM prediction and actual classification

对比图6和图7可知，从分类准确率看，对于桨距不对称故障这一对象，BP神经网络算法比SVM算法的分类效果好.

4 结 论

采用ReliefF算法对桨距角不对称故障相关参数进行特征选择，选取桨叶1桨距角偏差、桨叶2桨距角偏差、桨叶3桨距角偏差、功率因数设定值、机舱位置、塔架加速度、传动系统加速度和机舱旋转这8个特征参数，避免了“维数灾难”.采用BP神经网络对桨距角不对称故障进行分类，发现该算法可有效分辨出是否发生了桨距角不对称故障，其准确率高于SVM算法.该方法有利于现场操作人员及时判断故障类型，掌握故障信息，进行故障维护，从而减少风电场经济损失.

［1］徐大平，高峰，吕跃刚.基于混杂系统的风力发电机组建模与控制［J］.动力工程，2009，29（4）：369－374.XU Daping，GAO Feng，LÜ Yuegang.Modelling and control of wind turbine based on hybrid system［J］.Journal of Power Engineering，2009，29（4）：369－374.

［2］吴娜，孙丽玲，杨普.风力机状态监测与故障诊断技术研究［J］.华北水利水电学院学报，2012，33（2）：86－90.WU Na，SUN Liling，YANG Pu.Research on wind turbine condition monitoring and fault diagnosis［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，2012，33（2）：86－90.

［3］郭鹏，徐明，白楠，等.基于SCADA运行数据的风电机组塔架振动建模与监测［J］.中国电机工程学报，2013，33（5）：128－135.GUO Peng，XU Ming，BAI Nan，et al.Wind turbine tower vibration modeling and monitoring driven by SCADA data［J］.Proceedings of the CSEE，2013，33（5）：128－135.

［4］杨宏晖，陈兆基，戴键.基于自适应增强SVM集成算法的风机故障诊断［J］.检测技术，2010，29（7）：72－74.YANG Honghui，CHEN Zhaoji，DAI Jian.Fault diagnosis for fan based on self－adaptive boosting SVM ensemble［J］.Measurement ＆ Control Technology，2010，29（7）：72－74.

［5］龙泉，刘永前，杨勇平.基于粒子群优化BP神经网络的风电机组齿轮箱故障诊断方法［J］.太阳能学报，2012，33（1）：120－124.LONG Quan，LIU Yongqian，YANG Yongping.Fault diagnosis method of wind turbine gearbox based on BP neural network trained by particle swarm optimization algorithm［J］.Acta Energiae Solaris Sinica，2012，33（1）：120－124.

［6］杨飞虎.特征选择算法及其在网络流量识别中的应用研究［D］.南京：南京邮电大学，2012.

［7］KUSIAK A，VERMA A.A data－mining approach to monitoring wind turbines［J］.IEEE Transactions on Sustainable Energy，2012，3（1）：150－157.

［8］杨志新，段美军.ReliefF算法在雷达辐射源信号识别中的应用［J］.成都大学学报，2012，31（2）：151－153.YANG Zhixin，DUAN Meijun.Application of ReliefF algorithm in radar emitter signal recognition［J］.Journal of Chengdu University，2012，31（2）：151－153.

［9］李宗杰，梁海峰.基于特征选择和K－means聚类预处理的风电场功率预测［C］／／中国高等学校电力系统及其自动化专业第二十七届学术年会.北京：中国电机工程学会，2012.

［10］郭嘉.回声状态网络分类方法及其应用研究［D］.哈尔滨：哈尔滨工业大学，2011.

［11］KUSIAK A，VERMA A.A data－driven approach for monitoring blade pitch faults in wind turbines［J］.IEEE Transactions on Sustainable Energy，2011，2（1）：87－96.

［12］韩英莉，颜云辉.基于BP神经网络的带钢表面缺陷的识别与分类［J］.仪器仪表学报，2006，27（12）：1692－1694.HAN Yingli，YAN Yunhui.Discernment and classification of banding strip surface defect based on BP neural network［J］.Chinese Journal of Scientific Instrument，2006，27（12）：1692－1694.

［13］黄金花，彭晖.风电场短期风电功率的神经网络方法预测研究［J］.电工电气，2009（9）：57－60.HUANG Jinhua，PENG Hui.Study of wind power short－term prediction of wind farm based on neural network［J］.Jiangsu Electrical Apparatus，2009（9）：57－60.