伪攻角反馈驾驶仪的极点配置设计方法*

郑鹍鹏，陈星阳，李海峰

(中国空空导弹研究院，河南 洛阳 471009)

0 引言

伪攻角反馈驾驶仪是三回路过载驾驶仪的一种典型结构[1]。与经典的Raytheon三回路驾驶仪[2-5]相比，其增稳回路采用伪攻角反馈，可以消除经典三回路驾驶仪的静差，使闭环增益精确为1，同时能保持较好的时域、频域响应特性以及鲁棒性能，因此在战术导弹上得到广泛的应用。

三回路驾驶仪具有加速度、姿态角(或伪攻角)、姿态角速率3个反馈回路，可以应用极点配置法进行设计[6-9]。若忽略舵机、滤波器等高频部件动态特性的影响，则可以建立闭环极点与系统控制增益的解析关系，从而形成便于工程应用的驾驶仪设计方法。但是目前已有的设计方法主要是针对经典三回路驾驶仪[2-10]，文献[1]给出了伪攻角反馈驾驶仪的结构特点分析和极点配置设计方案，但并未给出控制增益与闭环极点的解析关系；同时，现有的驾驶仪设计方法普遍缺少闭环极点参数与带宽选择的指导性原则。

本文首先从伪攻角反馈驾驶仪的数学模型出发，给出了控制增益与闭环极点、开环截止频率的解析关系式。然后分别阐述了系统时域响应、高频部件带宽、舵机角速率极限及稳定裕度指标对系统截止频率、闭环极点配置形成的约束，进而给出了设计参数选择的指导原则，形成了自洽的驾驶仪设计方案。

1 导弹自动驾驶仪数学模型

1.1 开环系统

若忽略舵机、结构传感器、陀螺及加速度计等高频部件的动态特性，可得到简化的驾驶仪框图如图1所示。

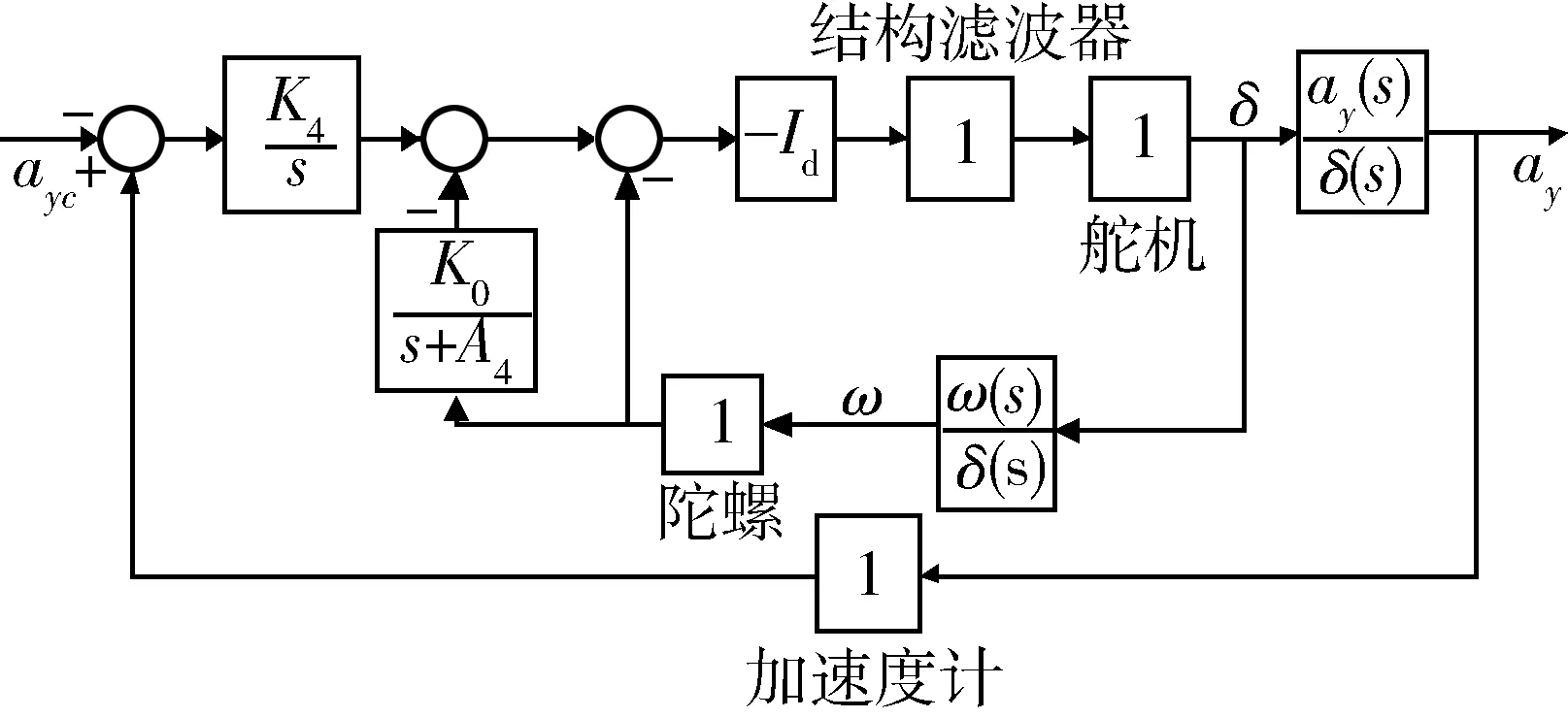
图1 伪攻角反馈自动驾驶仪简化框图 Fig.1 Simplified structure diagram of autopilot with pseudo angle of attack feedback

导弹本体传递函数为

(1)

式中：Ba=a1+a4；Ca=a2+a1a4；ωα=(a3a4-a2a5)/a3；Cz=(a3a4-a2a5)/a5；a1～a5为弹体动力学系数[11]。

将系统在舵机处断开，得到系统开环传递函数为

(2)

一般取A4≈ωα，则开环传递函数为3阶函数，一般形式为

(3)

式中：

(4)

由开环传函HG的幅值为1，可获得系统截止频率ωcr，即

HG(jωcr)=1.

(5)

一般来说，系统开环截止频率远大于导弹本体特征频率，从而可得

ωcr≈N2=Ida3-IdK4va5.

(6)

工程设计中通常将ωcr作为系统带宽的指标[7-9]。

1.2 闭环系统

结合式(3)可得到系统闭环传递函数为

(7)

理想三阶系统的极点配置形式通常是1个实极点与1对共轭极点，即有

s3+(Ba+N2)s2+(Ca+N1)s+N0=
(s+A)(s2+2ξωs+ω2)=
s3+(A+2ξω)s2+(w2+2Aξω)s+Aω2.

(8)

a1+a4+ωcr=A+2ξω,

(9)

a2+a1a4+Ida3ωα+IdK0a3-IdK4va5a1=
ω2+2Aξω,

(10)

IdK4va5Cz=Aω2.

(11)

值得注意的是式(9)建立了系统开环截止频率ωcr与闭环极点之间的关系，即闭环极点的实部之和近似等于ωcr。

在驾驶仪设计过程中，开环截止频率ωcr通常比共轭极点自然频率ω更具实际意义，因此将ωcr、阻尼比ξ、实极点-A作为取定的期望参数，ω以及3个控制增益Id,K0，K4作为未知量，综合式(6)及式(9)～(11)可得到控制增益的解析表达式：

(12)

2 参数选择原则

第1节建立了自动驾驶仪控制增益与系统开环截止频率、闭环极点之间的解析关系。本节将主要讨论闭环极点与开环截止频率的选取原则。

2.1 极点配置共圆准则

三阶系统的闭环等效时间常数(响应至指令63%的时间)近似为[3]

(13)

将式(9)代入式(13)，可得

(14)

(15)

进而可得τt的最小值为

(16)

由式(15)可知，当系统开环截止频率ωcr确定后，为使系统时间常数达到最小，通常将3个极点配置于同一圆上，该圆半径与ωcr及阻尼比ξ相关。

由式(16)可知，系统响应快速性与ωcr成反比，ωcr越大，系统响应越快。但ωcr不能无限制取大值，其取值受到高频部件带宽及舵机角速率限制等因素的制约。

2.2 高频部件带宽的约束

系统开环截止频率ωcr的选择首先受到舵机等高频部件响应特性的制约。为保证系统稳定性，且高频部件特性不对系统响应造成较大影响，工程上一般将驾驶仪开环截止频率ωcr取为高频部件等效带宽ωact的1/5～1/3[8]，保证高频部件在频率ωcr处引起的相移不超过30°。

2.3 舵机角速率极限的约束

作为执行机构的舵机在跟随指令过程中，舵偏转速率是有限的。自动驾驶仪设计时需要考虑这一约束。由式(7)出发，可得到加速度指令到舵偏角速率的闭环传递函数

(17)

将式(8)，(11)带入式(17)，归一化得到

(18)

式中：τ=1/A；T=1/ω；K=Ca/(va5Cz)；n2=1/Ca；n1=1/Ba。

记δc=Kayc，即δc为加速度指令ayc对应的稳态舵偏。若对式(18)进行部分分式分解，则有

(19)

式中：k0，k1，k2分别为不同模态的系数，显然有k0T2+k2τ=n2，k02ξT+k1τ+k2=n1，k0+k1=n0。通过拉普拉斯反变换可得到输入为阶跃响应指令时的舵偏角时域响应函数，即有

(20)

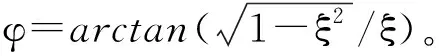
对式(20)求导，可得到舵偏角速率的时域响应函数

(21)

典型阶跃响应下舵偏角速率最大值[12]出现在初始时刻，由式(21)，并结合式(17)～(19)可得

(22)

按照共圆原则配置极点，将Ca=a2+a1a4以及式(15)代入式(22)，可得

(23)

(24)

式中:δc max为最大需用舵偏，进一步可得到对于ωcr的约束公式

(25)

2.4 开环相位裕度

导弹自动驾驶仪设计必须保证鲁棒性，一般要求系统相位裕度>40°。对于图1所示的简化三回路驾驶仪，若其在穿越频率处具有70°左右的相位超前，一般就能保证满足考虑舵机、结构滤波器等部件后完整系统的稳定裕度要求。

将式(6),(9)～(11)代入式(3),则系统开环函数可表达为

(26)

将s=jωcr代入式(18),可得

(27)

(28)

进而可得到简化系统相位裕度的近似值为

(29)

若要求系统开环裕度>γ(rad)，则有

(30)

将式(9)代入式(30),可得

(u-1)x2+ωcrx-a2-k<0,

(31)

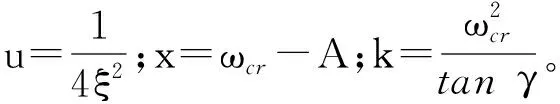
求解不等式(31),可得

(32)

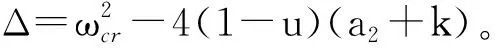
2.5 小结

综上所述，可以对系统带宽参数及极点选择的设计准则归纳如下：

(1) 系统开环截止频率的选择应考虑舵机等高频部件带宽ωact及舵机角速率极限的约束，其选取准则为

ωcr=min(ωcr1,ωcr2).

(33)

(2) 为保证制导大回路的稳定性，自动驾驶仪应具有足够的阻尼[3]。一般将其共轭极点阻尼比ξ取>0.7的数值。

(3) 3个闭环极点按共圆配置，配置圆半径由式(15)确定，这样可以保证同样带宽下系统时域响应最快。

(4) 为满足系统稳定裕度要求，系统带宽、阻尼比和极点选择应满足式(32)。

3 算例验证

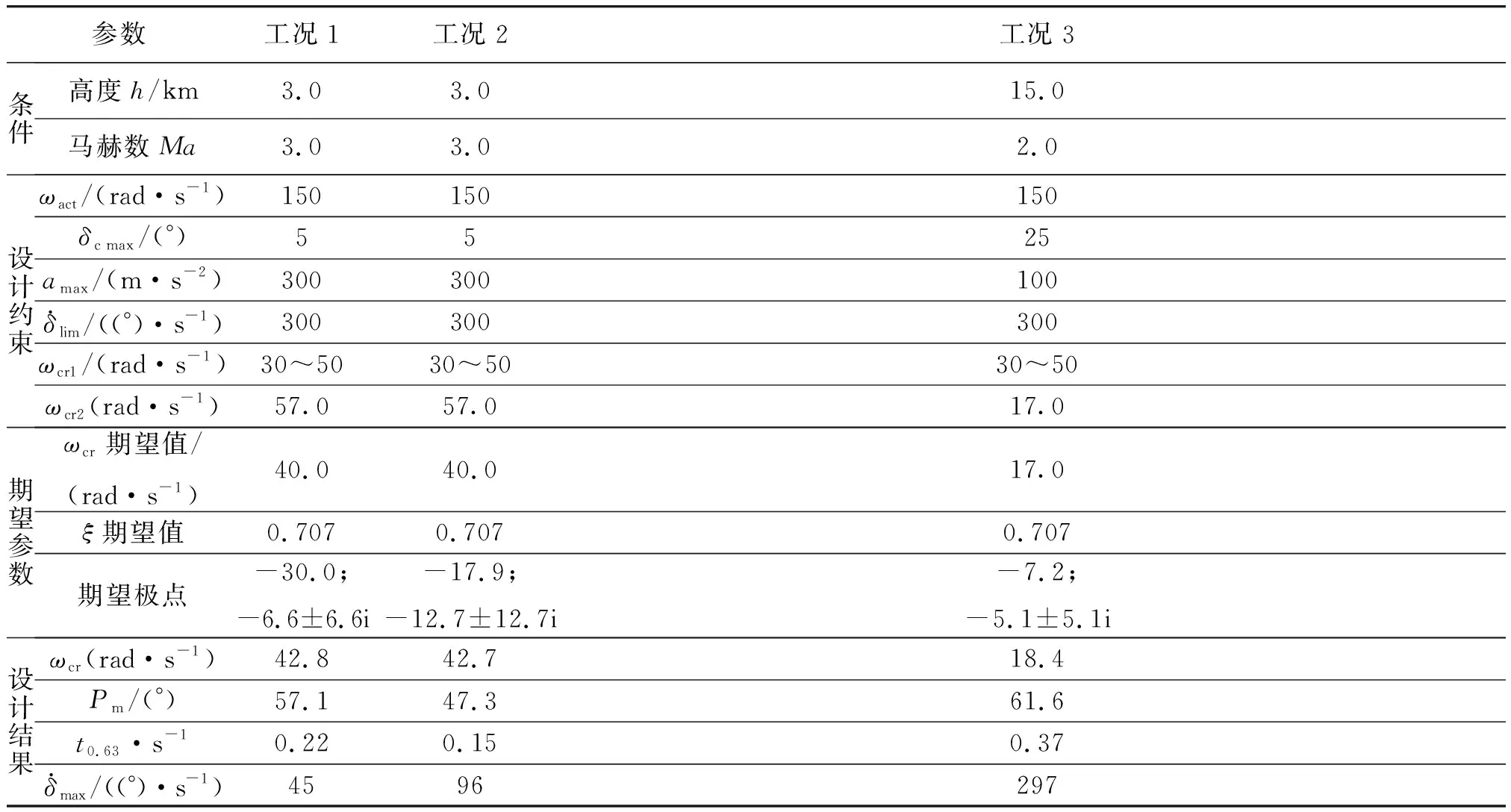
表1 不同工况下设计约束与设计结果

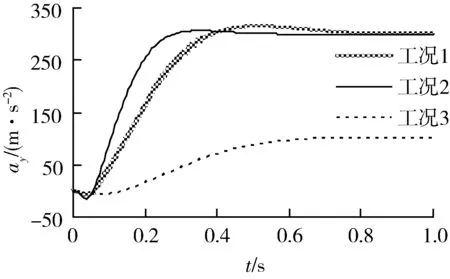
图2 加速度响应 Fig.2 Response of acceleration

图3 舵偏角响应Fig.3 Response of fin deflection angle

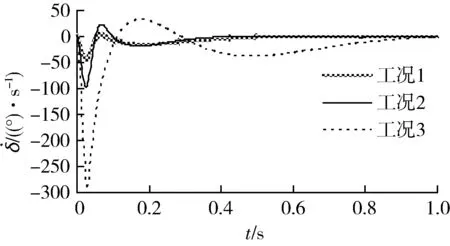
图4 舵偏角速度响应Fig.4 Response of fin rate

从图2～4和表1中可以看出：

(1) 低空大动压条件下需用舵偏小，系统带宽主要受舵机等高频部件带宽约束；高空小动压条件下需用舵偏大，舵偏角速率限制为主导约束。

(2) 与工况1相比，工况2的时域响应明显较快，表明相同带宽下，闭环极点按2.1节共圆准则配置，可以保证更快的响应时间。

(3) 设计结果具有较好的时域和频域性能，表明本文所提出的驾驶仪设计方法有效。

4 结束语

本文首先建立了伪攻角反馈驾驶仪控制增益与开环截止频率及闭环极点的解析关系，然后提出了系统极点配置及开环截止频率选取的指导原则，指出在系统开环截止频率一定的前提下，闭环极点按共圆配置，可获得最快时域响应特性；开环截止频率选择则受到高频部件带宽及舵偏角速率极限的约束。基于此形成了自洽的驾驶仪设计方法，本方法兼顾了系统的时域与频域性能，其有效性通过算例得以验证。

参考文献：

[1] 王辉,林德福,祁载康. 导弹伪攻角反馈三回路驾驶仪设计分析[J].系统工程与电子技术, 2012, 34(1): 129-135.

WANG Hui, LIN De-fu, QI Zai-kang. Design and Analysis of Missile Three-Loop Autopilot with Pseudo-Angle of Attack Feedback[J].System Engineering and Electronics, 2012, 34(1): 129-135.

[2] NESLINE F W, NESLINE M L. How Autopilot Requirement Constrain the Aerodynamic Design of Homing Missiles[C]∥In Proc. of American Control Conference, San Diego, CA,1984,716-730.

[3] 王娟利, 祁载康. 三回路自动驾驶仪特点分析[J]. 北京理工大学学报, 2006, 26(3): 239-243.

WANG Juan-li, QI Zai-kang. Analysis of a Three-Loop Autopilot[J].Journal of Beijing Institute of Technology, 2006, 26(3): 239-243.

[4] MRAEK C P, RIDGELY D B. Missile Longitudinal Autopilots: Comparison of Multiple Three-Loop Topologies [R]. AIAA 2005-6380, 2005.

[5] MRAEK C P, RIDGELY D B. Missile Longitudinal Autopilots: Connections Between Optimal Control and Classical Topologics [R]. AIAA 2005-6381, 2005.

[6] 朱敬举,祁载康,夏群力. 三回路驾驶仪的极点配置方法设计[J]. 弹箭与制导学报, 2007, 27(4): 8-12.

ZHU Jing-ju, QI Zai-kang, XIA Qun-li. Pole Assignment Method for Three-Loop Autopilot Design[J]. Journal of Projectiles Rockets Missiles and Guidance, 2007, 27(4): 8-12.

[7] ZARCHAN P.Tactical and Strategic Missile Guidance[M].5th ed. Washington D C: American Institute of Aeronautics and Astronautics,2007.

[8] 温求遒,夏群力,祁载康. 三回路驾驶仪开环穿越频率约束极点配置设计[J]. 系统工程与电子技术, 2009, 31(2):420-423.

WEN Qiu-qiu, XIA Qun-li, QI Zai-kang. Pole Placement Design with Open Loop Crossover Frequency Constraint for Three-Loop Autopilot[J]. System Engineering and Electronics Technology, 2009, 31(2):420-423.

[9] 刁兆师, 单家元. 基于预测校正的三回路驾驶仪极点配置设计[J]. 系统工程与电子技术, 2012, 34(8): 1668-1674.

DIAO Zhao-shi, SHAN Jia-yuan. Pole Assignment Design with Prediction-Correction Technology for Three-Loop Autopilots [J]. System Engineering and Electronics Technology, 2012, 34(8):1668-1674.

[10] 盛永智. 轨控直接力/气动力复合控制拦截弹的自动驾驶仪设计[J]. 现代防御技术, 2009, 37(6):51-54.

SHENG Yong-zhi. Autopilot Design for Interceptor with Blended Control by Aerodynamic Force and Divert Thruster[J]. Modern Defence Technology, 2009, 37(6):51-54.

[11] 程云龙. 防空导弹自动驾驶仪设计[M]. 北京：中国宇航出版社, 1994.

CHENG Yun-long. Autopilot of Surface to Air Missile Design[M]. Beijing: Chinese Astronautics Press, 1994.

[12] В Г斯维特洛夫,И С戈卢别夫.防空导弹设计[M].北京:中国宇航出版社,2004.

Светлов В Г, Голубев И С. Air Defense Missile Design [M]. Beijing: Chinese Astronautics Press, 2004.