舵面热颤振分析研究*

张永超，朱瑾，刘炜

(北京电子工程总体研究所，北京 100854)

0 引言

国内外航空航天技术的发展，促使飞行器朝着飞行高度更高、飞行速度更快的方向发展。随着飞行速度的提高，气动加热现象引起了广泛关注。气动加热在使飞行器本身温度升高的同时，由于温度分布不均匀而在结构内部产生了热应力[1-2]。因此在飞行过程中，飞行器同时承受着气动力载荷与气动热载荷。此时结构的弹性力、惯性力、气动力和热应力之间相互耦合，引发气动热弹性问题[3]。

国内外对气动热弹性问题的研究取得了一定成果。文献[4]中对一个简单的机翼模型进行了热颤振分析。结果显示温度在(0℃，90℃)范围内，温度增高65℃,热应力改变结构刚度分布，导致颤振临界速度降低约2/3。由于采用的模型比较特殊，其计算结果虽然有一定的合理性，但是不具有普遍性。

文献[5]中提出了一种分步式热颤振工程分析方法，通过非线性热应力分析，获取高超声速飞行器在气动热环境下的结构振动模态，结合非定常气动力的计算分析结构热颤振特性。这种方法在设计中进行了初步应用。文献[6]中采用分层求解思路分析了不同翼面构型情况下热环境对颤振结果的影响。结果显示，对于全动舵面，舵轴刚度对固有频率的影响很大，但舵轴温度变化很小，所以在弦向变化的温度场下，固有频率和颤振特性变化不大。但是在其建模过程中没有考虑折叠机构的影响。

本文主要以带有折叠机构的超声速空气舵为研究对象，在不同温度分布情况下分析其热振动特性和热颤振特性。

1 热颤振分析流程

飞行器在飞行过程中，由于飞行高度、速度、姿态等都随时间变化，气动热环境也随着飞行时间变化，飞行器结构内部温度场分布是时变的。由于结构温度变化的时间尺度与结构动态响应的时间尺度相差很大，所以分析时可以认为温度分布是准定常的，因而可以在典型的温度分布状态下进行模态分析。对于气动弹性的稳定性计算，一般只考虑结构做微幅振动，结构动态变形引起的热流脉冲与飞行器基本姿态下的热流分布相比是小量，因此可以不计其对温度分布的影响[7]。

基于上述原因，可采用弱耦合的热-结构分析方法建立气动弹性仿真模型，在某一时刻将温度场看作稳态，分析给定该温度场下的结构振动特性变化。先进行结构温度分布分析，再进行受热结构模态分析，结合高超声速非定常气动力的计算结果，分析结构气动弹性问题[8-9]，如图1所示。

图1 热颤振分析流程Fig.1 Flow of thermal flutter

1.1 热刚度

温度变化对结构固有特性的影响主要由对刚度矩阵K的影响所体现，主要表现在2个方面：温度改变材料弹性模量；结构温度变化不均匀，在结构内部产生热应力，使结构局部刚度增加或减小，改变结构初始刚度分布。热应力产生的附加刚度为[10-11]

(1)

受热后结构刚度矩阵为

K=K0+Kσ,

(2)

式中：K0为弹性模量随温度变化后的结构刚度矩阵；K为考虑热应力对刚度影响后的结构刚度矩阵。

1.2 颤振分析

采用超声速气动面法求空气舵的非定常气动力。在热环境下，热气动弹性颤振方程[12]为

(3)

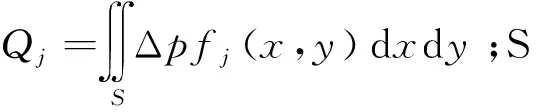
对颤振方程，一般采用P-k法求解，即定一系列速度，反复迭代求颤振速度。

2 算例仿真分析

2.1 热模态分析

高超声速导弹的全动舵面采用小展弦比梯形气动外形。用实体单元建立骨架模型，蒙皮采用壳单元，折叠机构采用MPC及Spring模拟，舵面结构有限元模型如图2所示。通过调节Sping刚度，使有限元模型常温固有频率与常温下舵面试验结果值一致。约束舵轴截面上节点的6个自由度，使舵面处于固支状态。

图2 舵面有限元模型Fig.2 Finite element modal of rudder

材料选用钛合金，只考虑其弹性模量随温度变化，如表1所示。

表1 弹性模量Table 1 Elasticity modulus

当舵面温度依次从20℃升高到100，200，300，400，500 ℃，在只考虑材料弹性模量变化(情况1)和同时考虑弹性模量变化与热应力影响(情况2)这2种情况下，舵面固有频率随温度的变化趋势如图3所示。随着温度的增高，弹性模量降低导致舵面固有频率降低，一阶弯曲和二阶扭转频率之间差值减小；计及温度变化产生的热应力影响后，固有频率下降幅度增大，且呈非线性趋势下降。这点说明对于算例中使用的模型，热应力对结构刚度分布的影响比较大。

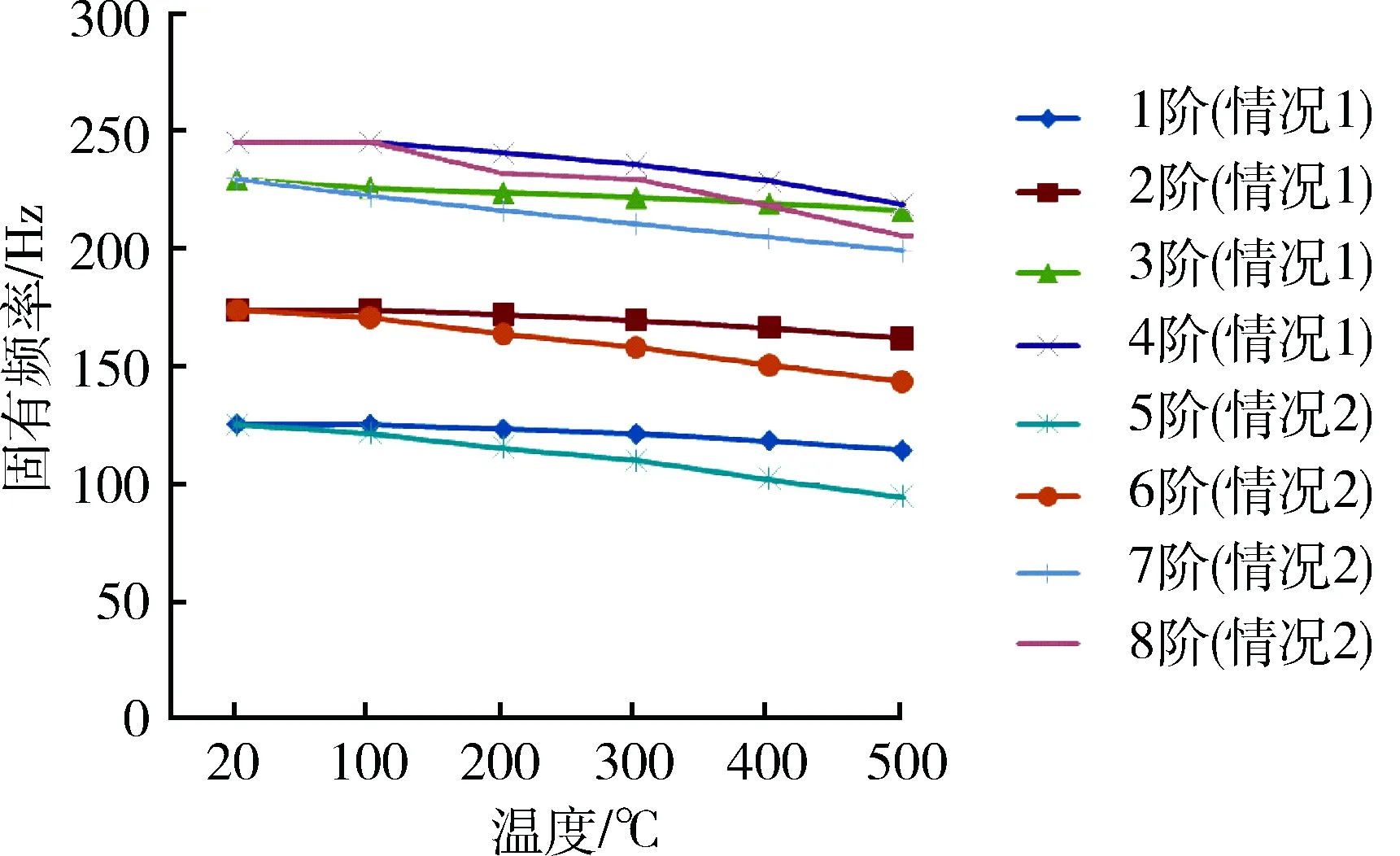
图3 固有频率随温度变化Fig.3 Natural frequency changes with temperature

当结构温度场分布不均匀，迎风面、背风面保持相同的100℃温差时，令迎风面温度增高。温度沿舵面厚度方向线性变化如图4所示。舵面由于不均匀温度场的存在产生翘曲变形如图5所示。图6表明由于MPC和节点约束的存在，转轴处热应力比较大，特别是采用MPC单元模拟折叠机构的部分。图7显示计及热应力后的固有频率的变化幅度也要比只考虑弹性模量时大，呈非线性趋势下降。

图4 温度场Fig.4 Temperature field

图5 热变形Fig.5 Thermal deformation

图6 热应力Fig.6 Thermal stress

图7 固有频率随迎风面温度变化Fig.7 Natural frequency changes with windward temperature

2.2 热颤振分析

首先分析舵面处于20 ℃均匀温度场下的颤振特性，计算结果如图8所示，固支状态下单独舵面的发散速度为3 788 m/s。

在均匀温度温度场下，发散速度随温度增高而减小，如图9所示；舵面迎风与背风面温度相差100 ℃时，舵面发散速度随迎风面温度增加而降低，如图10所示。当迎风面温度固定为400 ℃，随着迎风面与背风面温差的增大，发散速度增高，如图11所示。在均匀温度场或舵面迎风面和背风面温差较小时，舵面发散速度随温度的增高而降低，当舵面温差增加，舵面内热应力增加，使得发散速度随温差增大而增高。

图8 颤振计算结果Fig.8 Result of flutter

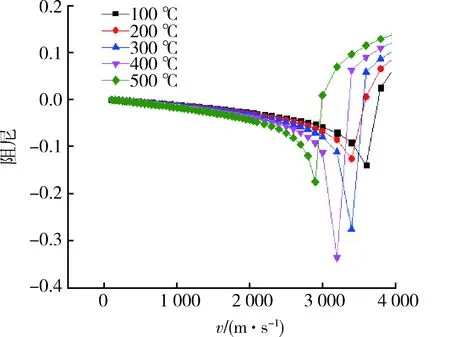
图9 v-g图(均匀温度场)Fig.9 v-g plot (even temperature field)

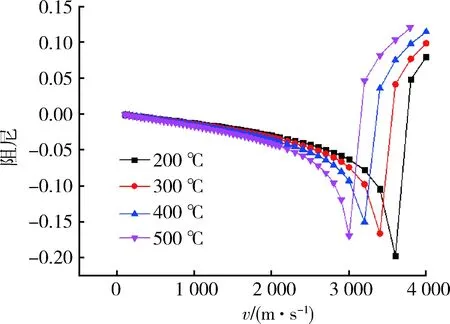
图10 v-g图(温差100℃)Fig.10 v-g plot (temperature difference of 100℃)

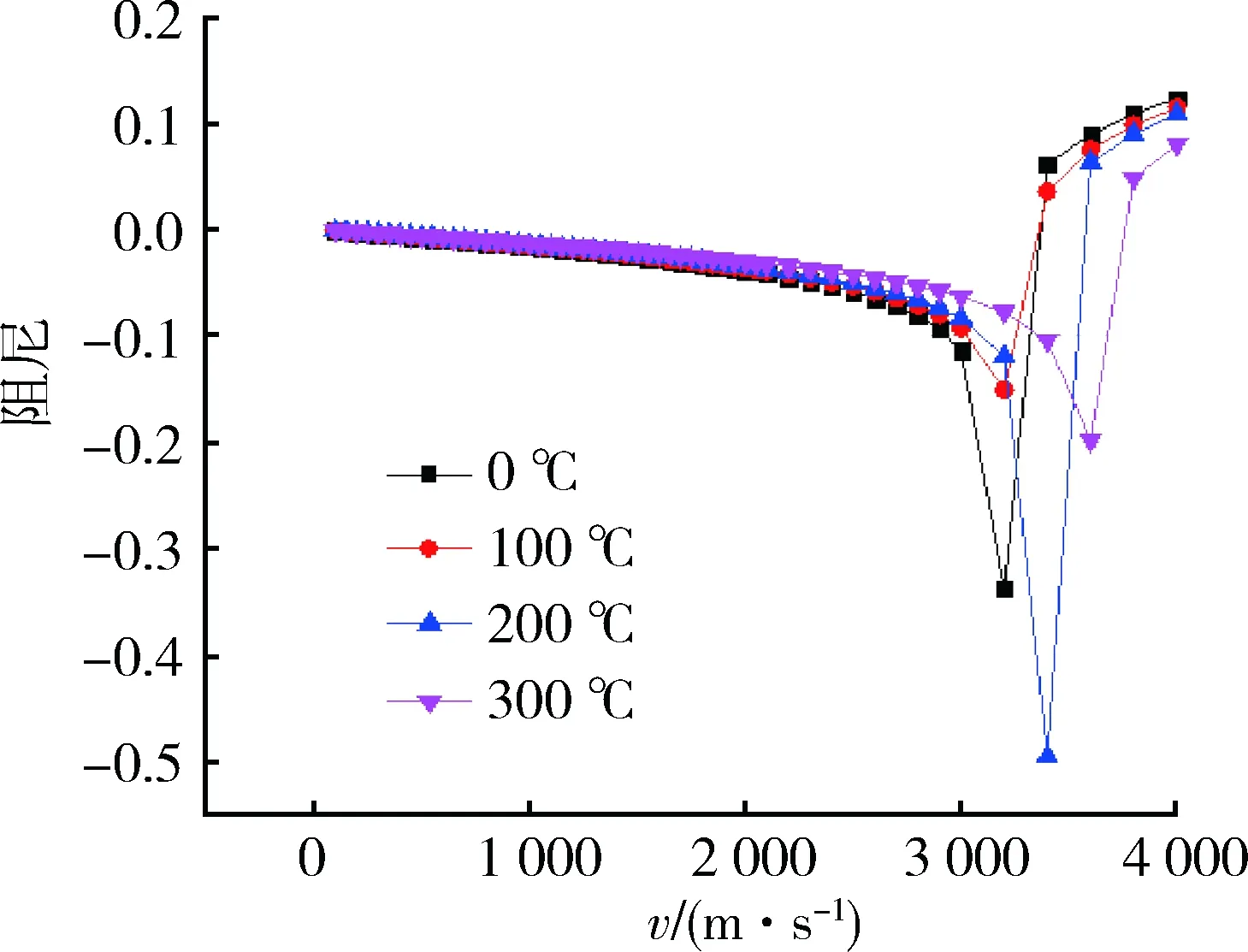
图11 v-g图(迎风面400℃)Fig.11 v-g plot (windward temperature of 400℃)

3 结束语

本文中算例是比较典型高超声速导弹的空气舵，在计算马赫数范围内，不产生颤振现象。但是其分析结果还是揭示出舵面的热振动特性，以及对颤振特性的影响。

舵面温度增高使得空气舵固有频率降低，发散速度降低。计及热应力后，固有频率的下降幅度明显增大，说明热应力的影响比弹性模量变化的影响大。

均匀温度场下舵面温度增高使舵面发散速度降低；随着舵面上下表面温差的增大，热应力增大，使得舵面发散速度增大。

由于舵面有限元模型需要模拟折叠机构，使得在转轴处产生较高的热应力。由计算结果可知热应力对结构刚度的影响比较大，所以折叠机构的建模方法对舵面热振动特性和热颤振特性有很大影响，还需要进行进一步研究。

参考文献：

[1] MCNAMARA J J. Hypersonic Aerothermoelastic Studies for Reusable Launch Vehicles[R]. AIAA,2004-1590, 2004.

[2] 钮耀斌，王中伟.气动加热下高速尾翼的热颤振分析[J].飞机设计,2009,29(5):13-15.

NIU Yao-bin, WANG Zhong-wei. Analysis of Tail Thermal Flutter Under Aerodynamic Heating [J]. Aircrafa Design, 2009,29(5):13-15.

[3] Jack J McNamara. Aeroelastic and Aerothermoelastic Analysis of Hypersonic Vehicles: Currrent Status and Future Trends[C]∥ Honolulu, Hawaii:48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamic, and Materials Conference, 2007:23-26.

[4] 陈文俊. MSC/NASTRAN程序中一个气动热弹性考题的计算结果[J]. 战术导弹技术，1999(4)：32-38.

CHEN Wen-jun. The Results of a Program About Aerothermoelastic in MSC/NASTRAN[J]. Tactical Missle Technology,1999(4):32-38.

[5] 谭光辉，李秋彦，冉玉国,等.一种高超音速热颤振工程分析方法[C]∥第十一届全国空气弹性学术交流会,2003,21(4): 481-486.

TAN Guang-hui, LI Qiu-yan, RAN Yu-guo, et al. Analysis Method for Thermal Flutter of Supersonic Vehicle[C]∥11th Countrywide Aeroelasticity Acadymic Conference,2003,21(4):481-486.

[6] 吴志刚，惠俊鹏，杨超.高超声速下翼面的热颤振工程分析[J].北京航空航天大学学报,2005,31(3),270-273.

WU Zhi-gang, HUI Jun-peng, YANG Chao. Hypcrsonic Acrothcrmoclastic Analysis of Wings[J].Journal of Beijing University of Aeronautics And Astronautics, 2005,31(3):270-273.

[7] Jack JMcNamara,Adam J Culler. Aerothermoelastic Modeling Consideration for Hypersonic Vehicle[C]∥ 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference.

[8] SPAIN C, SOISTMANN D,Eparker.An Overview of Selected NASP Aeroelastic Studies at NASA-Langley Research Center[R].AIAA:1900-5218.

[9] 吕继航，杨茂，陈凤明.超音速舵面热气动弹性仿真[J].计算机仿真，2010，(27)3，43-46.

LÜ Ji-hang, YANG Mao, CHEN Feng-ming. Aerothermoelastic Simulation of Supersonic Missle Rudder[J]. Computer Simulation,2010,(27)3:43-46.

[10] 李增文,林立军,关世义.超声速全动翼面热颤振特性分析[J].战术导弹技术,2008(5):36-39.

LI Zeng-wen, LIN Li-jun, GUAN Shi-yi. Research on the Thermal Flutter Characteristics of Hypersonic All-move Wing[J]. Tactical Missle Technology, 2008(5):36-39.

[11] 杨超.飞行器气动弹性原理[M].北京：北京航空航天大学出版社,2011:52-53.

YANG Chao.Aeroelasticity Theory of Aircraft [M].Beijing:Beihang University Press,2011:52-53.

[12] 张伟伟,夏巍,叶正寅.一种超高音速热气动弹性数值仿真研究方法[J].工程力学,2006,23(2):41-46.

ZHANG Wei-wei, XIA Wei, YE Zheng-yin. A Numerical Method for Hypersonic Aerothermoelasticity[J]. Engineering Mechanics,2006,23(2):41-46.