微电网中分布式电源逆变器数字多环反馈控制方法

李国庆，王星宇，王 鹤

(东北电力大学电气工程学院，吉林吉林132012)

很多分布式电源都需要通过电力电子接口设备与微电网相连。实现直流-交流变换的逆变器是微电网运行与控制的重要基础，逆变器控制的主要目标是控制输出电压的幅值和相角并输出一定的有功和无功功率［1-3］。文献［4］、［5］主要研究微电网中逆变器的控制方法，对微电网的并网及孤岛运行方式分别进行研究，详细介绍了逆变器的恒功率控制(PQ控制)和恒压恒频控制(V-f控制)方法。文献［6］提出了一种微电网中逆变器的下垂控制方法，模拟高压电力系统中发电机的频率和端电压与所输出的有功功率和无功功率之间的下垂特性来协调多个分布式电源。

微电网中含有大量的非线性和不平衡负荷，会造成严重的负序和谐波干扰，微电网中逆变器的控制方法需要具有抑制非线性和不平衡负荷干扰的能力。文献［7］提出了一种分布式电源逆变器的正序/负序电流控制方法，能够使输出电压有效避免非线性负荷的影响。文献［8］-［9］将分布式电源逆变器模仿有源滤波器运行，通过注入谐波电流来抵消非线性或不平衡负荷引起的干扰，改善电压波形。微电网中负荷的非线性和不平衡是同时存在的，现有文献大多没有同时计及它们的影响。此外，注入谐波电流改善电压波形的方法只能针对其中某些谐波或不平衡进行抵消，而且向微电网中注入谐波电流会引入新的谐波源，同时减少了分布式电源正常的功率输出［10］。

本文对微电网中分布式电源逆变器的数字多环反馈控制方法进行研究，在不向微电网中注入谐波电流的情况下改善分布式电源逆变器的输出电压波形。采用无差拍控制提高算法的跟踪速度，采用重复控制方法抑制非线性和不平衡负荷引起的周期性扰动，并通过模拟下垂特性与其他分布式电源逆变器协调，仿真实验结果证明了本文提出方法的有效性。

1 微电网与分布式电源的结构与组成

1.1 微电网的结构和组成

本文选择的微电网主体结构，见图1。

微电网中心控制器(MicroGrid Central Controller，MGCC)安装在中压-低压变电站，对微电网进行统一的协调控制;负荷控制器(Load Controller，LC)和微电源控制器(Microsource Controller，MC)从属于MGCC，分别控制具体的负荷和微电源;MGCC和LC、MC之间需要建立可靠的通信连接［11］。本文采用的微电网结构中包含有2个直流分布式电源和3个负荷。直流分布式电源通过逆变器向微电网供电;负荷1、负荷2和负荷3分别是三相对称线性负荷、三相不对称线性负荷和三相对称非线性负荷。

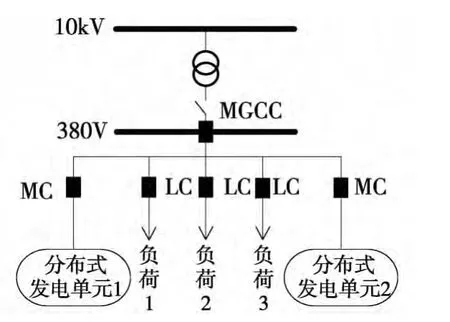
图1 微电网结构与组成

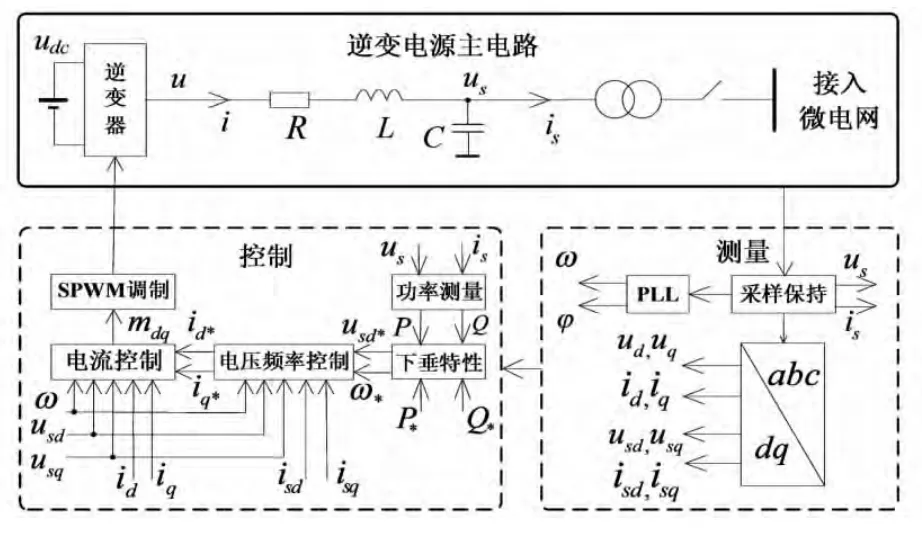
图2 直流分布式发电单元结构与组成

1.2 直流分布式发电单元

图2为直流分布式发电单元由主电路部分、测量部分和控制部分组成。主电路部分包括直流电源、逆变器、LC滤波器、连接变压器和断路器，电源发出的直流电经逆变和滤波后通过连接变压器和断路器接入微电网;测量部分由采样保持电路、数字锁相环(PLL)和abc/dq变换模块组成，通过采样保持电路对主电路中的电压和电流进行数字测量，由数字PLL跟踪频率ω和相位φ，并通过abc/dq变换得到所需的同步旋转坐标系下的各个电压和电流分量;逆变器控制部分由电流控制环、电压控制环和功率控制器3个部分组成，将在下一节详细介绍。

2 分布式电源逆变器多环反馈控制方法

在本文提出的分布式电源逆变器多环反馈控制方法中，电流控制内环实现参考值的快速跟踪;中间的电压控制环负责控制逆变器输出的电压幅值和频率;功率控制器采用下垂控制方式确定逆变器输出电压和频率的参考值［12］。

2.1 电流控制环

电流控制环是多环反馈控制方法中的最内环，电流控制环的输出直接通过SPWM方法控制逆变器交流侧电流的d轴和q轴分量。从图2中的主电路可以看出，逆变器交流侧电流i、电压u和分布式发电单元输出电压us之间满足下述关系

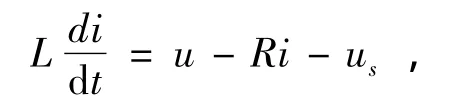
将逆变器交流侧电压u表示为mudc/2，其中udc是逆变器直流侧电压，m是SPWM的调制比，在此基础上将(1)式改写成同步旋转坐标系下的解耦形式

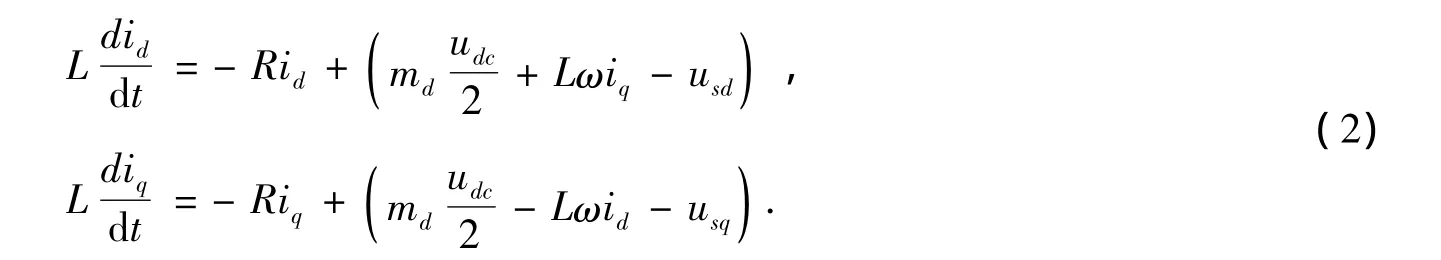
式中:下标d和下标q分别表示各个量的d轴和q轴分量，ω是电压和电流的频率。

对上式以周期Ts采样，得到离散形式

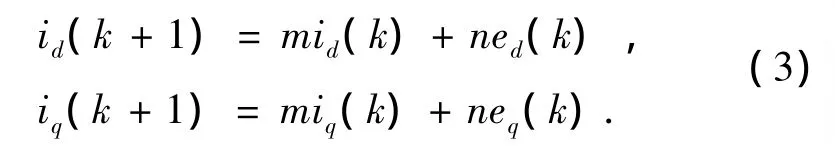
式中:

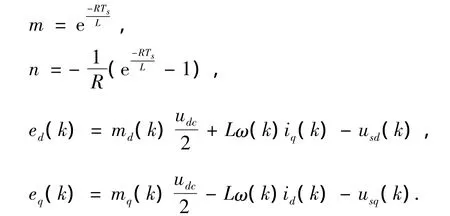
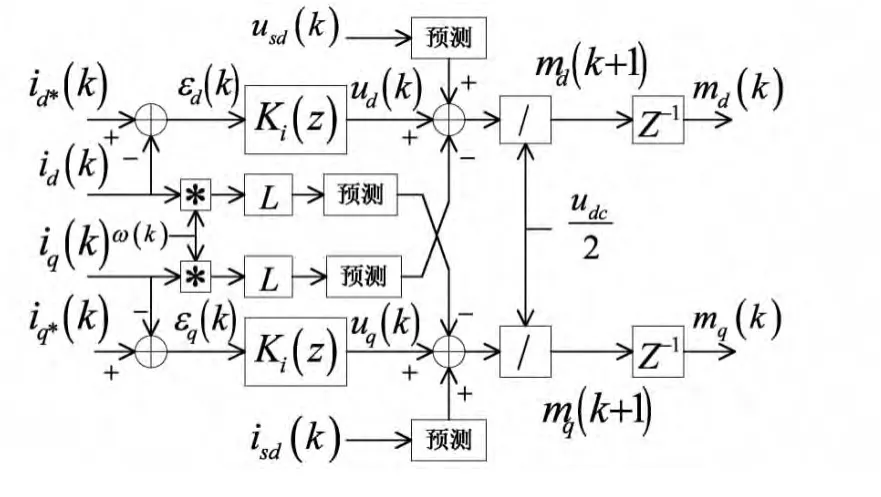
图3 电流控制环原理框图

根据(3)式，设计图3为电流控制环，输入为电流控制参考值id*(k)和iq*(k)，输出为调制比md(k)和mq(k)。

控制环的输出md(k)和mq(k)是通过对md(k+1)和mq(k+1)延迟一个采样周期得到的，引入延迟是为了避免微处理器计算过程中对数据资源的竞争引起冲突。计算md(k+1)和mq(k+1)需要用到测量信号usd(k)、usq(k)、id(k)和iq(k)的预测值usd(k+1)、usq(k+1)、id(k+1)和iq(k+1)，对k+1时刻的预测可以由下式得到

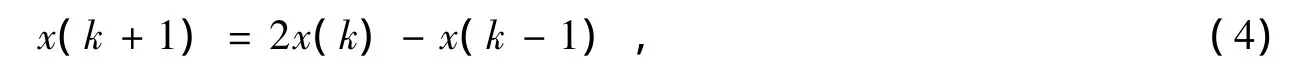
对(3)式做Z变换，根据电流控制环的输入和输出，以d轴为例将电流控制环控制对象的数学模型描述如下式所示，用q轴描述的结果完全相同。

假设(4)式的预测过程是准确的，设计图3中的补偿环节Ki(z)为

可以使电流控制环的闭环极点位于Z平面的原点，得到稳定快速的闭环响应，仍然以d轴为例，整个电流控制环的闭环传递函数为

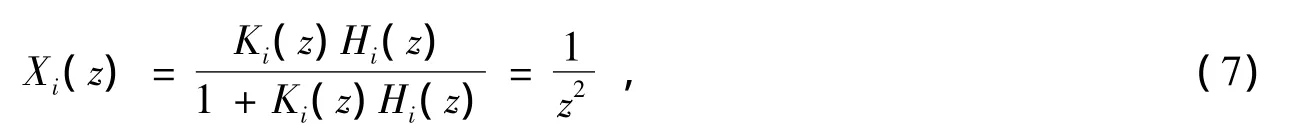
这种闭环极点的设置方法属于无差拍控制，这样就实现了在两个采用周期内对电流控制参考值的快速跟踪［13］。

2.2 电压控制环

电压控制环在多环反馈控制方法中处于中间位置，在电流控制环基础上实现对分布式发电单元输出电压和频率的控制。本文借助数字PLL实现这一过程，假设分布式发电单元输出电压是三相对称的，幅值和相角分别为U和θ，PLL输出相角为θp，则根据派克变换公式，可以得到分布式发电单元输出电压的d轴分量和q轴分量为［14］

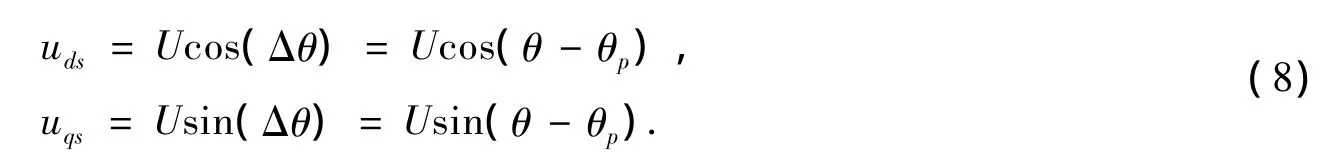
当Δθ=0时，usd=U，usq=0。可以通过控制usq=0来实现数字PLL输出相角对分布式发电单元输出电压相角的跟踪，还可以通过控制usd来控制输出电压的幅值。本文中使用频率误差信号ω*(k)-ω(k)确定usq*(k)，当误差信号为0时，usq*=0，保持输出频率不变;当频率与参考值之间存在偏差时，usq*为一个较小的非零值，可以使输出频率跟踪参考值的变化。

和电流控制环类似，从图2中的主电路可以看出，逆变器交流侧电压u、电流i和分布式发电单元输出电流is之间满足下述关系

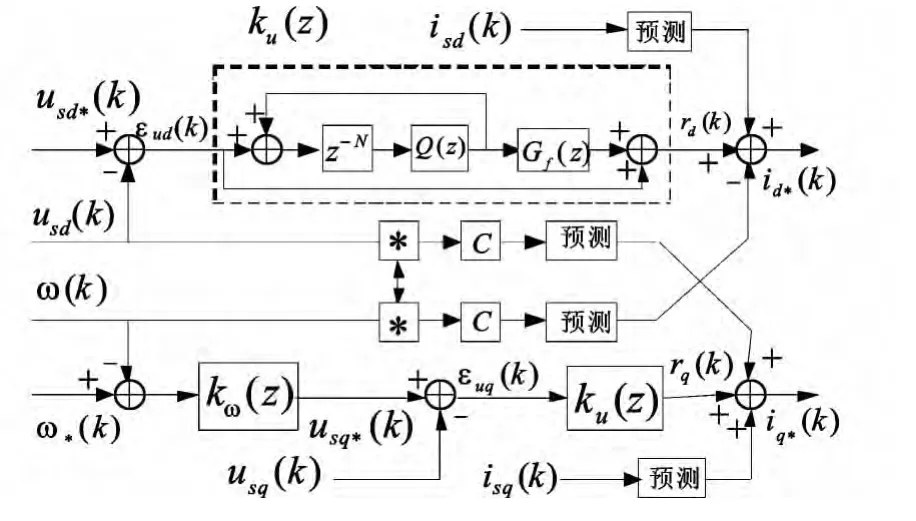
图4 电压控制环原理框图

按照和电流控制环同样的方法，可以得到上式在同步旋转坐标系下的离散形式

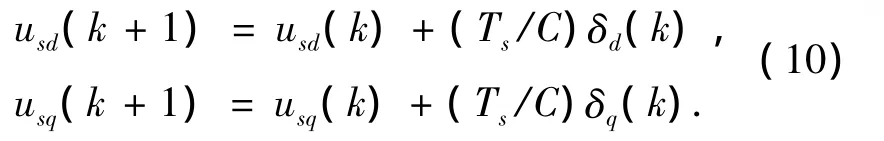
其中

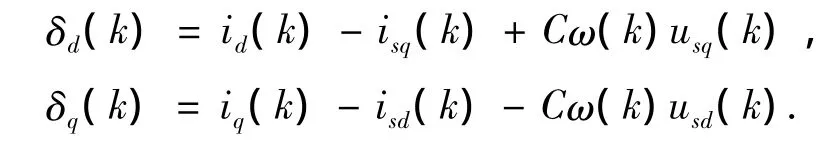
由(10)式，结合上述对电压幅值和频率控制的分析，可以得到图4的电压控制环原理框图，输入为电压幅值参考值usd*(k)和频率参考值ω*(k)，输出为电流控制参考值id*(k)和iq*(k)。

与电流控制环不同，电压控制环中的预测过程为2步预测，本文中采用下式实现

数字多环反馈控制方法中，数字PLL的输出为

式中:kf是滤波增益。由上式，可以通过控制usq(k)实现对ω(k)的控制。图4中，频率误差信号经过补偿环节kω(z)得到usq*(k)。因为usq*(k)的稳态值趋近于0，所以可以简单地选择kω(z)=kω，实现ω(k)对ω*(k)的零稳态误差跟踪。

usd(k)和usq(k)的误差信号经过相同的补偿环节ku(z)，如果负荷是三相对称的线性负荷，则ku(z)可以用PI控制器来实现;但是在不平衡或非线性负荷的影响下，电压和电流测量信号的d轴和q轴分量会出现各种谐波干扰，使电压幅值和频率的控制失效。本文采用重复控制方法代替PI控制器抑制这些周期性的扰动，实现不平衡或非线性负荷下电压幅值和频率的解耦控制。在仿真实验环节，本文对比了电压控制环中PI控制和本文提出的控制方法。

图4中usd(k)的控制环给出了本文中ku(z)的具体实现。根据重复控制的基本原理，可以设计

其中，D=T/Ts，T为干扰信号的周期。由上式，ku(z)中的闭环负反馈会对干扰信号及其谐波分量有很强的抑制作用。因为D不一定是整数，图4中选取N个先进先出的存储单元组成延迟阵列z-N，用整数N作为D的主要整数部分。

图4中的Q(z)用来补偿N近似D的误差，本文中选择m阶FIR滤波器实现对e-s(D-N)Ts的近似

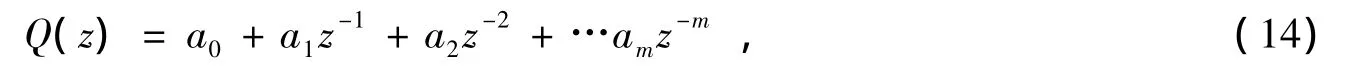
采用对近似误差求极小值的方法，并结合拉格朗日插值公式，可以得到FIR滤波器的系数为

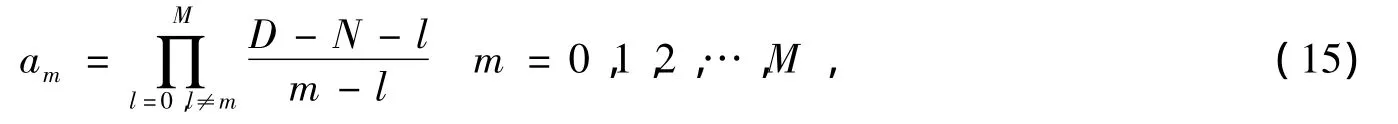
Q(z)的设计需要综合考虑FIR滤波器的阶数和频率响应对e-s(D-N)Ts的近似精度，本文中选择M=9，N=int(D)-4，即 e-s(D-N)Ts中(D-N)的整数部分为4。

下面分析电压控制环的闭环稳定性，与电流控制环类似，电压控制环的控制对象可以用d轴分量为例表示为

本文中选择Gf(z)=z3，通过引入相位超前环节来补偿Hu(z)闭环引起的相位滞后。由文献［15］可知，对含重复控制的闭环系统稳定性分析可以通过对再生谱的分析解决。本文中定义再生谱为重复控制部分中z-N的开环传递函数的倒数

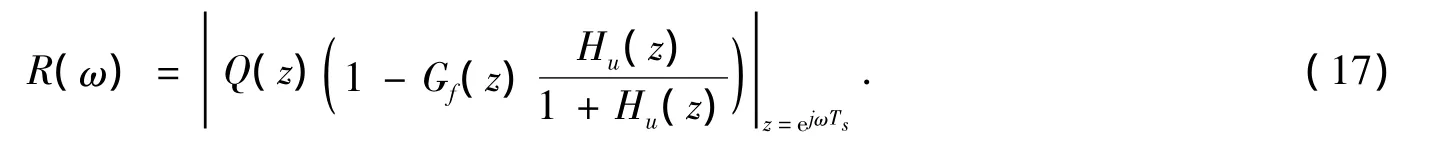
可以证明，本文中设计的重复控制方法满足文献［15］中闭环稳定的三个条件，即Q(z)和Gf(z)是稳定的、Hu(z)是闭环稳定的、在所有频率下R(ω)＜1，所以本文中含有重复控制的电压控制环是闭环稳定的。

2.3 功率控制器

在多环反馈控制方法中，功率控制器通过模拟下垂特性实现多个分布式电源之间的协调，能够通过下垂系数的设置自动实现负荷在多个分布式电源之间的分配，原理框图见图5。

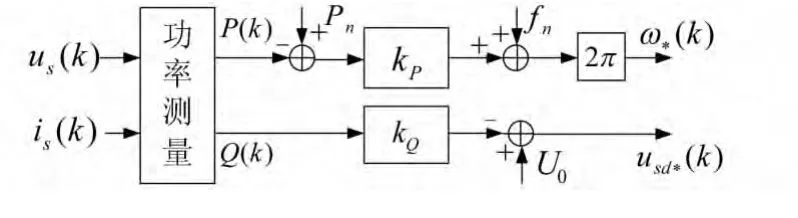
图5 功率控制器原理框图

为了避免非线性和不平衡负荷对功率测量的影响，本文选择文献［16］中基于低通滤波的功率测量方法。由图5，下垂特性可以表示为

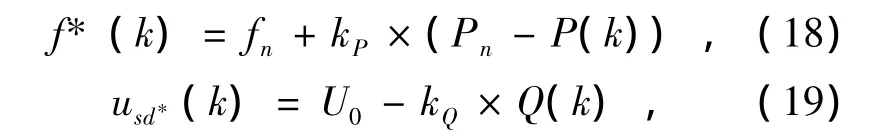
式中:P(k)和Q(k)分别是逆变器发出的有功功率和无功功率，f*(k)和usd*(k)表示逆变器的频率和电压，fn和U0分别是其额定值。Pn是逆变器在额定频率下输出的功率。kP、kQ是下垂系数，可通过下式求得

4 仿真分析

本文采用PSCAD/EMTDC工具软件对微电网中的分布式电源逆变器进行仿真研究。本文共有2个算例，重点对比电压控制环中采用PI控制和本文方法的仿真实验结果，并给出仿真过程中微电网频率和电压的变化，反映功率控制器对下垂特性的模拟。图2中的直流电源采用理想电压源，主电路和控制部分主要参数见表1。

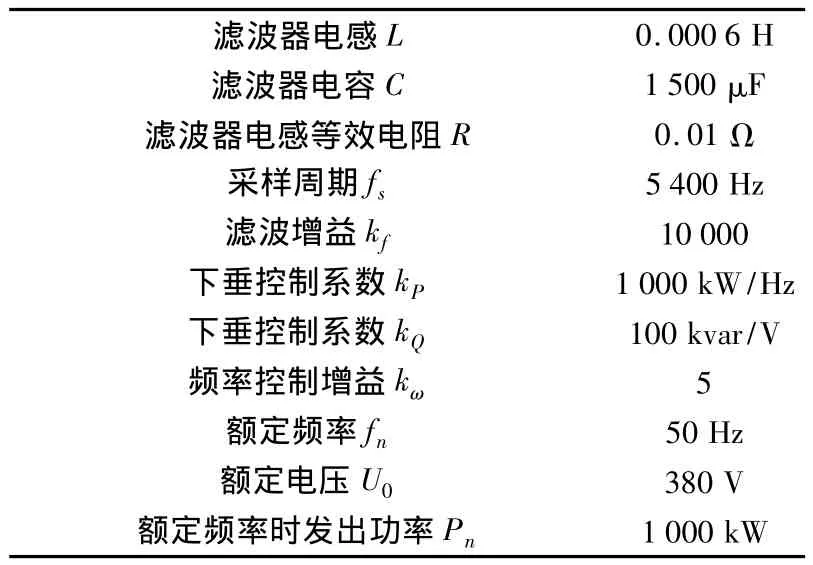
表1 仿真参数

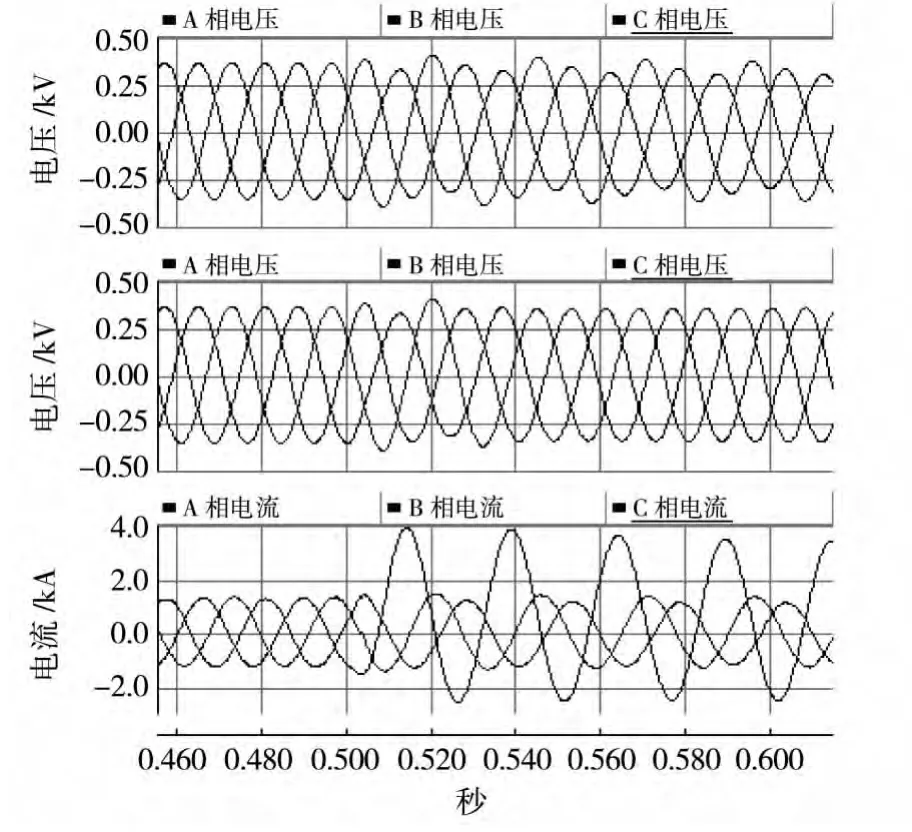
图6 电压电流波形

算例1:图1的微电网孤岛运行，2个直流分布式发电单元同时为负荷供电，仿真开始时只接入负荷1(三相对称线性负荷，每相300 kW，100 kVar)，在0.5 s时刻接入负荷2(不对称线性负荷，A相500 kW，500 kVar)。图6和图7给出了仿真结果。

图6中上面2个子图分别是电压控制环采用PI控制和本文方法时分布式发电单元输出电压波形，第3个子图是电流波形。从图中可以看出，在5 s时刻，微电网接入线性不平衡负荷后，A相电流突然增大。采用PI控制的分布式发电单元输出电压波形受不平衡负荷影响负序分量明显增加;而采用本文方法的分布式发电单元通过重复控制方法抑制周期性扰动，在短暂的调整后就能够继续输出三相对称的电压波形。

图7中上面2个子图分别给出了2种控制方法下逆变器输出的d轴和q轴电压分量对比，仿真结果表明:在5 s时刻后，PI控制电压d轴和q轴分量受到周期性干扰，而本文方法能够有效地抑制这种干扰。第3个子图是2种控制方法下逆变器输出电压负序分量与正序分量之比，在5 s时刻后PI控制的电压负序分量明显增加，本文方法负序分量增加较小。综上所述，图7能够得到与图6相同的结论，本文方法在不平衡负荷条件下能够保持较好的输出电压波形。

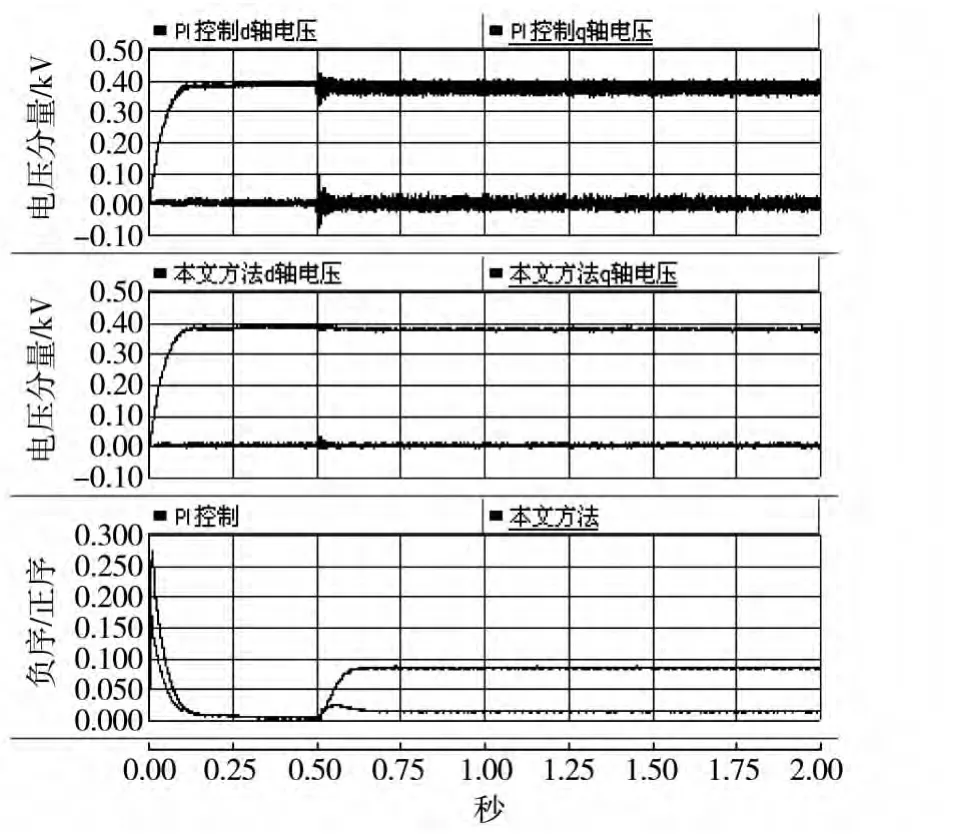
图7 电压分量和负序正序电压比值

算例2:仿真的初始情况与算例1完全相同，在0.5 s时刻改为接入负荷3(对称非线性负荷，三相共300 kW，300 kVar)，仿真结果如图8和图9所示。

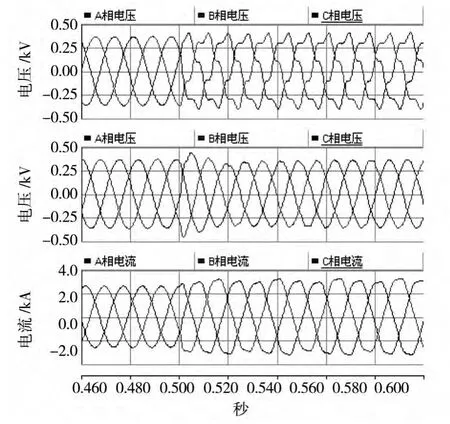
图8 电压电流波形

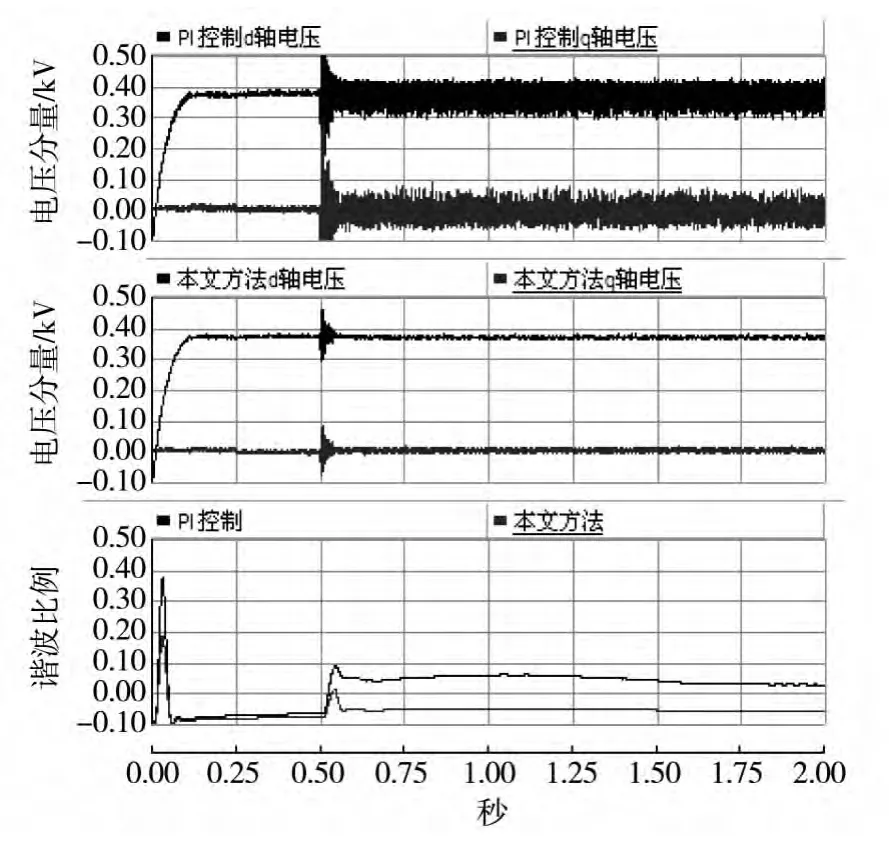
图9 电压分量和谐波比例

图8和图9与图6和图7描述的仿真基本一致，在5 s时刻微电网接入非线性负荷使电流发生畸变，电流变化导致PI控制电压波形发生畸变;本文方法通过抑制周期性的扰动仍然能够输出较理想的电压波形。图9中可以看出PI控制中非线性负荷引起的d轴和q轴分量的周期性干扰更加严重，而本文方法仍然能够很好的抑制这种干扰。图9中第3个子图描述的是电压谐波所占信号的比例，可以看出5 s时刻后PI控制输出电压谐波干扰严重，而本文方法输出谐波较小。

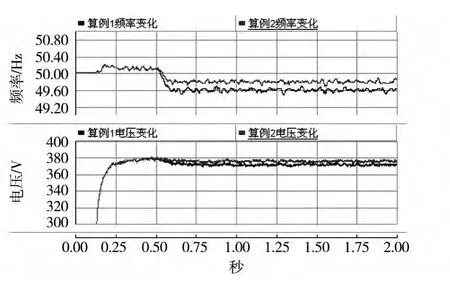
图10 频率和电压的自动调节

从2个算例的仿真实验结果都可以看出采用无差拍控制的电流控制环能够实现很高的响应速度，快速地跟踪参考值的变化。图10给出了2个算例中逆变器输出的频率和电压随负荷变化自动调节的仿真结果。图中前0.2 s为仿真的初始过渡状态，0.2 s后可以看出随着负荷的变化各个逆变器自动调节输出的电压幅值和频率，实现对微电网电压幅值和频率的自动控制。本文算例中2个分布式发电单元逆变器采用相同的下垂系数，承担相同的负荷，可以通过选择不同的下垂系数实现负荷在多个分布式电源之间的合理分配。

5 结 论

本文对逆变器的控制方法进行研究，结合无差拍控制、重复控制等先进控制技术，提出了一种适合于微电网中分布式电源使用的数字多环反馈控制方法。仿真实验结果表明本文提出的方法可以实现较高的响应速度，并且能够克服不平衡和非线性负荷的影响，在各种负荷情况下维持较好的电压输出波形。此外，本文提出的方法还通过模拟下垂特性实现微电网电压幅值和频率的自动控制，实现多个分布式电源之间的协调。

［1］鲁宗相，王彩霞，闵勇，等.微网研究综述［J］.电力系统自动化，2007，31(19):100-107.

［2］丁明，张颖媛，茆美琴.微网研究中的关键技术［J］.电网技术，2009，33(11):6-11.

［3］Chowdhury S，Chowdhury S P，Crossley P.Microgrids and active distribution networks［M］.London，U.K.:IET，2009:122-127.

［4］郭力，王成山.含多种分布式电源的微网动态仿真［J］.电力系统自动化，2009，33(2):82-86.

［5］LOPES J A P，MOREIRA C L，MADUREIRA A G.Defining control strategies for analyzing microgrids islanded operation［J］.IEEE Trans.Power Systems，2006，21(2):916-924.

［6］MOHAMED Y，SAADANY E.Adaptive decentralized droop controller to preserve power sharing stability of paralleled inverters in distributed generation microgrids［J］.IEEE Trans.Power Electron.，2008，23(6):2806-2816.

［7］C.K.Sao and P.W.Lehn.Voltage balancing of converter fed microgrids with single phase loads［C］.Presented at the IEEE Power Energy Soc.General Meeting，Pittsburgh，PA，Jul.2008.

［8］李心广，赖声礼，秦华标，等.电网的无功及三相不平衡综合补偿研究［J］.电网技术，2003，23(10):63-66.

［9］罗安，欧剑波，唐杰，等.补偿配电网电压不平衡的静止同步补偿器控制方法研究［J］.中国电机工程学报，2009，29(6):55-60.

［10］C.K.Sao and P.W.Lehn Control and power management of converter fed microgrid［J］.IEEE Trans.Power Syst.，2008，23(3):1088-1098.

［11］王成山，肖朝霞，王守相.微网综合控制与分析［J］.电力系统自动化，2008，32(7):98-103.

［12］黄伟，孙昶辉，吴子平，等.含分布式发电系统的微网技术研究综述［J］.电网技术，2009，33(9):14-18.

［13］T.Kawabata，T.Miyashita，and Y.Yamamoto.Dead beat control of three phase PWM inverter［J］.IEEE Trans.Power Electron，5(1):21-28.

［14］加德纳.锁相环技术［M］.3版.姚剑清，译.北京:人民邮电出版社，2007:408-418.

［15］Mohammad B.Delghavi，Amirnaser Yazdani.Islanded-mode control of electronically coupled distributed resource units under unbalanced and nolinear load conditions［J］.IEEE Trans.Power Delivery，2011，26(2):661-673.

［16］Mohamed Y，Saadany E.Adaptive decentralized droop controller to preserve power sharing stability of paralleled inverters in distributed generation microgrids［J］.IEEE Trans.Power Electron.，2008，23(6):2806-2816.

［17］顾和荣，杨子龙，邬伟扬.并网逆变器输出电流滞环跟踪控制技术研究［J］.中国电机工程学报，2006，26(9):108-112.

［18］何流.逆变器并网及孤岛检测技术的研究［D］.江苏:南京航空航天大学电气工程学科学位论文，2009:19.

［19］郑宏，史玉立，孙玉坤，等.微电网并网逆变器下垂控制策略的改进［J］.农业工程学报，2012，28(6):191-196.

［20］范元亮，苗逸群.基于下垂控制结构微网小扰动稳定分析［J］.电力系统保护与控制，2012，40(4):1-13.