具有无穷时滞的“食物有限”差分系统的持久性

阮育清

（厦门工商旅游学校，福建厦门361024）

具有无穷时滞的“食物有限”差分系统的持久性

阮育清

（厦门工商旅游学校，福建厦门361024）

研究具有无穷时滞的“食物有限”差分模型。通过对系统进行详尽的分析，得到了系统的无条件持久的结果。

持久性；差分；无穷时滞；食物有限

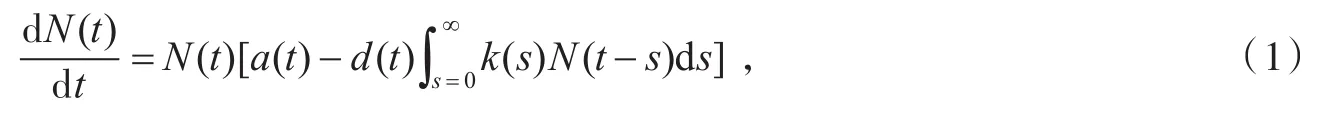
早在1992年，Gopalsamy［1］就提出了如下Logistic方程：并证明了该方程在a(t)，d(t)为有相同周期的连续函数的条件下存在唯一的周期解。Seifert［2］则研究了该系统的持久性，证明了当a(t)，d(t)均为概周期函数且满足时，系统（1）是持久的。徐建华［3］改进了文献［2］的结论，进一步证明了在除去条件（2）的情况下，系统（1）仍是持久的。

然而迄今为止，学者们对食物有限模型的研究仍较少见。本文考虑如下无穷时滞“食物有限”差分系统

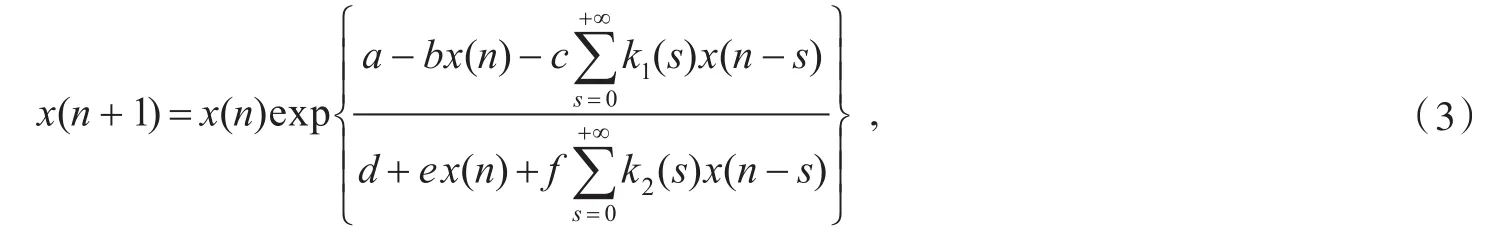
其中x(n)表示第n代种群的密度，表示历史种群对现代种群的影响，ki:[0，+∞)→[0，+∞)为有界非负序列，且满足

由图1可知系统（14）是持久的。数值模拟支持笔者的结论。

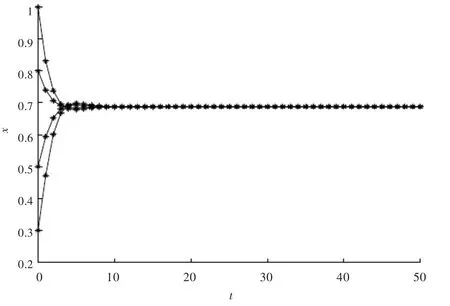
图1 系统（14）的具初值x(t)=0.3，0.5，0.8，1(t=…，-n，-n+1，…，-1，0)的数值模拟图Fig.1Numerical simulation diagram of system（14）with initial value x(t)=0.3，0.5，0.8，1(t=…，-n，-n+1，…，-1，0)

（References）

［1］GOPALSAMY K.Stability and oscillations in delay differential equations of population dynamics［M］.Dordrecht：Kluwer Academic Publisers Group，1992.

［2］SEIFERT G.Almost periodic solutions for delay logistic equations with almost periodic time dependence［J］.Differential In⁃tegral Equation，1996，9（2）：335-342.

［3］徐建华.无穷时滞Logistic方程的概周期解存在定理［J］.数学年刊，2002（3）：307-310.

［4］XU J B，TENG Z D.Permanence for a nonautonomous discrete single-species system with delays and feedback control［J］. Appl Math Lett，2010，23：949-954.

［5］JUAN H，TENG Z D，GAO S J.Permanence and global stability for nonautonomous N-species Lotka-valterra competitive system with impulses［J］.Nonlinear Anal Real World Appl，2010，11（3）：1882-1896.

［6］何尾莲.具连续时滞单种群反馈控制模型的持久性［J］.福州大学学报：自然科学版，2009，37（4）：468-477.

［7］CHEN F D，YANG J H，ChEN L J.Note on the persistent property of a feedback control system with delays［J］.Nonlinear Anal Real World Appl，2010，11（2）：1061-1066.

［8］YANG W S，LI X P，ChEN L J.Feedback control has no influence on the persistent property of a single species discrete model with time delays［J］.Math Comput Modelling，2011，54（9/10）：2007-2013.

［9］FAN Y H，WANG L L.Permanence for a discrete model with feedback control and delay［J］.Discrete Dyn Nat Soc，doi：10.1155/2008/945109.

（责任编辑：强士端）

Permanence of"Food-limited"Discrete System with Infinite Delays

RUAN Yuqing
（Xiamen Industrial&Commercial Tourism School，Xiamen 361024，Fujian，China）

A"food-limited"discrete model with infinite delays is studied.By giving the detail analy⁃sis of the system，obtains that the system is permanent unconditionally.

permanence；discrete；infinite delays；food-limited

O175.14

A

1673-0143（2014）06-0052-05

2014-03-15

阮育清（1985—），女，助讲，硕士，研究方向：生物数学。