CRH2型动车组在大跨度连续刚构桥上的制动响应分析

陈丹华，程海根

(华东交通大学土木建筑学院,南昌 330013)

CRH2型动车组在大跨度连续刚构桥上的制动响应分析

陈丹华，程海根

(华东交通大学土木建筑学院,南昌 330013)

为了研究大跨度连续刚构桥在CRH2型动车组制动力作用下的性能，建立了线路-桥梁有限元分析模型。依据动车组的制动减速度特性曲线，计算了车体的制动力时程。利用线性插值原理，编程计算了钢轨各节点的制动力时程。将轨面各节点的制动力时程和竖向力时程施加于结构，利用Midas有限元软件进行了动力响应分析。结果表明，主梁纵向变形具有累积性；制动力和竖向力联合作用下，连续刚构桥的纵向位移普遍较小，墩底纵向弯矩也在规范静力取值范围之内，表明动车组制动情况下连续刚构桥处于安全状态。

高速列车；制动；连续刚构；动力分析

随着我国经济的发展,高速铁路大规模兴建,伴随铁路建设的是列车不断提速,制动问题也受到了越来越多的关注。列车实施制动时,将对桥上轨面产生一个与运行方向相同的水平纵向力―――列车制动力。列车制动力由线路-桥梁结构系统共同承受。在制动荷载作用下,桥梁的主梁、桥墩的安全性直接影响到列车和旅客的安全。

近些年,高速铁路修建了大量的大跨度预应力桥梁,尤其是大跨度连续梁桥和连续刚构桥。但目前国内外对桥梁承受制动力的研究,荷载主要针对于普通重载列车［1]或公路汽车荷载,研究对象大多是公路或铁路的多跨简支梁桥或者斜拉桥［2],对高速铁路连续梁的研究不多［3],而对于连续刚构桥在高速列车制动力作用下的研究,几乎处于空白状态。

连续刚构桥由于上部主梁连续长度较长,行车舒适性较好,且连续刚构桥的桥墩与主梁固结,省去了主墩大吨位支座,有利于维修养护,但同时墩梁固结会使得梁上的纵向力传递到主墩,主墩受力是否合理,关系到上部桥梁和线路的安全问题。由于连续刚构桥主墩较高,墩顶位移和墩底受力就成为桥墩设计的控制条件。

由于铁路桥梁承受列车制动力的问题涉及列车、轨道、道床及桥梁结构形式,影响因素复杂,需要建立车-线-桥整体分析模型。但车辆-桥梁耦合作用是包含轮轨相互作用的复杂过程［4,5],本文将采用另一种简捷计算方法,将动车组各轮对作用于轨面的竖向力和水平力,作为移动荷载计算,根据高速动车组制动减速度特性得到随时间变化的车辆制动力时程,通过空间离散可得到轨面各节点所承受的制动力时程,将制动力时程和轮对竖向力(轴重)时程直接施加于线路桥梁整体分析模型,利用振型叠加法进行连续刚构桥的动力响应分析。

1 线路-桥梁整体分析模型

1.1 工程背景

桥梁属于新广州站及相关工程跨环城高速特大桥工程,桥孔布置为(94+168+94)m三跨预应力混凝土连续刚构,铁路等级为客运专线,双线铁路。全梁长356 m。主梁为单箱单室,顶宽13.4 m,底宽8.5 m。梁体变高度,端支座及边跨直线段和跨中处梁高为5.5 m,中墩处梁高11 m,梁高按圆曲线变化。腹板厚度在边支点和主墩处加厚,底板厚由跨中的0.5 m按圆曲线变化至中墩梁根部的1.3 m,中墩处加厚到1.8 m；全梁共设7道横隔梁。全梁按悬臂施工方法,共分89个梁段,中墩0号梁段长度13.0 m,一般梁段长度分成3.0 m、3.5 m和4.0 m,合龙段长度2.0 m,边跨直线段长11.0 m。梁体采用三向预应力体系。

主墩采用双薄壁桥墩,壁厚2.5 m,横桥向宽11 m,两侧倒圆,墩高25 m,桥面二期恒载集度185 kN/m。

1.2 有限元模型

采用有限元软件Midas 建立线路-桥梁动力分析模型。梁轨间的道床及扣件的刚度特性以纵向弹簧模拟［6],其他方向为刚性连接。根据国内外大量资料,梁轨相对位移为2 mm,为线路纵向阻力弹、塑性转变点。但在制动荷载作用下,梁轨相对位移总小于2 mm［7],故可按弹性阶段刚度取值。根据《铁路无缝线路设计规范》［8],竖向有载时线路纵向阻力在梁轨相对位移为2 mm时最大,为60 kN/m/线,所以本文计算模型中弹簧的纵向刚度取30 MN/m/m。各单元范围的弹簧刚度取上述每延米刚度乘以相应单元长度进行换算,换算后单位为MN/m或kN/m。

桥梁结构形式为上述356 m三跨连续刚构桥。双薄壁桥墩,墩底固结,墩顶与主梁三向固结。桥梁左右端为纵向活动支承。钢轨、主梁和桥墩采用梁单元模拟,遵循主梁构造变化及施工节段来划分单元。轨道采用我国无缝线路广泛使用的60 kg/m钢轨,并向桥梁左右端路基延伸40 m,以考虑纵向力向桥外的传递。线桥结构全长436 m,有限元分析模型如图1所示。

图1 线路桥梁有限元模型

2 CRH2型动车组制动力

CRH2型动车组的编组形式为4辆动车和4辆拖车,以1动1拖为一个制动单元,采用电气指令微机控制直通式电空制动系统［9-10]。动车组的制动指令由司机制动控制器发出电气指令,经列车信息控制系统传送到每辆车的制动控制单元,由电子控制单元进行运算,按照预定的减速度给定列车制动力。制动方式分为EB紧急制动和1～7级常用制动,图2是动车组速度-黏着模式控制所决定的制动减速度特性曲线［11- 12]。

图2 CRH2型动车组制动减速度特性曲线

本文考虑单线EB紧急制动工况,减速度特性为: 0～70 km/h时,a=1.122 2(m/s2)；70～118 km/h时, a=1.401 7-0.003 993 1v(m/s2)；118～200 km/h时, a=1.179-0.002 105 4v(m/s2)。制动过程中,认为各车辆减速度一致。

制动过程中车辆的减速力F=(1+r)m·a(kN)

其中,r为回转质量系数,CRH2型动车组属动力分散式,其r值取0.08；m为车辆质量,t；a为不同速度时的减速度,m/s2。

而减速力等于制动力加上动车组运行时的基本阻力。为了考虑最不利的制动力情况,本文忽略基本阻力影响,认为减速力全部由电空制动力提供。给定时间步长ΔT,在t+ΔT时刻,假定减速度为常量,利用数值积分法,编程计算制动过程中各时刻车体相应的速度、制动力、运行位置和时间。各车辆制动力随时间变化的时程曲线也由此得到。

本文计算时停车位置选在桥梁右端。动车组制动初速度为200 km/h,从距离桥梁1 361.85 m开始制动,经30.80 s动车组第一轮轴驶入桥梁左侧路基段, 57.46 s时第一轮轴停止于桥梁最右端,制动总距离1 717.85 m。

3 行车竖向力

由于桥梁两端设有纵向活动支座,不仅列车制动力会引起主梁和桥墩的纵向振动,而且行车竖向轮重荷载也会引起主梁产生纵向位移。为了分析行车移动荷载作用下桥梁的制动响应,需要在计入制动力时程的同时,将运行中各时刻的轮轴竖向轴重转换为线路轨面节点的竖向力荷载时程。

4 轨面节点制动力时程和竖向力时程

4.1 空间离散

按照动车组每个车体的质量、轮轴数,可将上述车辆制动力时程换算为各轮轴的制动力时程bj(t)；通过对运行位置的计算可得到各轮轴的位移时程xj(t)。为了方便对结构进行动力时程分析,需要将各车轮的制动力及竖向力(轴重)离散到线桥结构的轨面节点上去。

判断制动过程中任意时刻车轮与轨面节点间的相对位置关系,利用线性插值原理,将轮轴制动力离散到与之相邻的钢轨节点上去［13]。以bj(t)代表已知的各轮轴的制动力时程,轨面节点i和轮轴j的水平坐标分别为xi、xjk(t),以t时刻轨面节点区段［xi-1,xi+1]内进入jk-1～jk+1三个轮对为例,节点i所分配到的制动力Bi(t)为

编程计算制动过程中任意时刻车轮的位置,判断它与轨面节点间的位置关系,按(1)式计算得到轨面各节点的制动力时程曲线。

由车轮轴重产生的节点竖向荷载时程可用同样原理得到。

4.2 节点制动力时程和竖向力时程

CRH2型动车组基本参数为:4辆动车,4辆拖车,总长为201.4 m,其中头车长度25.7 m,中间车长度为25 m。固定轴距为2.5 m,转向架中心间距为17.5 m。列车定员时编组整体质量为408.5 t,各节车体的质量各不相同,最大轴重为140 kN,最小轴重为117 kN。

本文共分析计算了117个轨面节点的制动力时程和竖向力时程,得到了234条节点时程曲线。图3、图4示出了位于中跨的轨面54号节点的制动力时程和竖向力时程。

5 动力方程

线-桥结构系统动力方程为

图3 轨面54号节点制动力时程

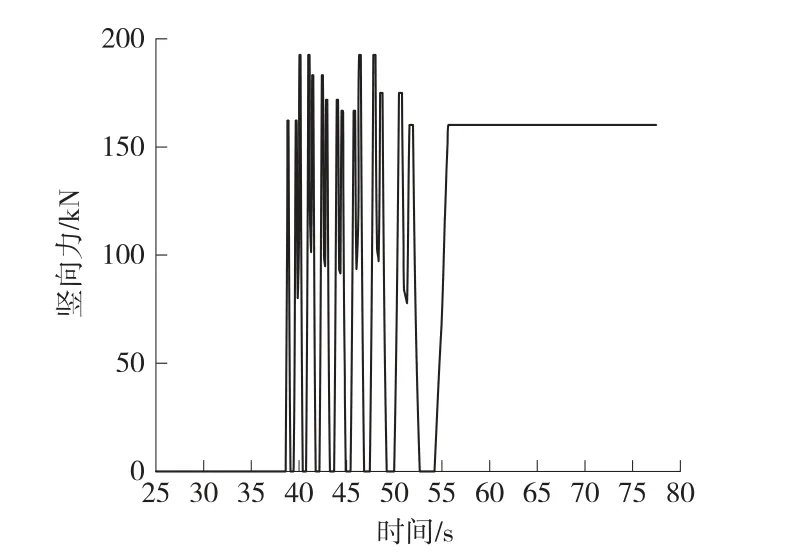
图4 轨面54号节点竖向力时程

式中,［M]、［K]分别为线路和桥梁结构系统的质量和刚度矩阵；［C]为阻尼矩阵,本文采用Rayleigh阻尼；F(t)为荷载向量,由线桥结构的轨面节点的制动力荷载向量和竖向力荷载向量组成。采用振型叠加法进行动力响应的时程分析。分析时间间隔取0.01 s,计算终止时间取停车后20 s。

6 动力响应分析

本文进行了以下3种情况的加载分析:制动荷载单独作用、移动竖向荷载单独作用、制动力和竖向力联合作用。

图5、图6是制动力和竖向力各自单独作用下的主梁位移时程。列车从距离桥梁1 361.85 m开始制动,经30.80 s动车组第一个轮轴到达桥梁左侧路基段,32.20 s到达连续刚构桥的左支点,引起线路-桥梁的动力响应,在57.46 s第一个轮轴停止在桥梁右端支点处。停车瞬间制动力消失,引起了纵向振动,并逐渐衰减。但停车后轮轴竖向力仍然存在,直到计算终止(取停车后20 s)。

从图5看到,列车在40.12 s之前还处于制动减速度上升区段,由此导致各节点纵向水平位移的增长,在40.12 s之后,此时列车速度降至70 km/h以下,制动减速度稳定在1.122 2 m/s2直到停车,所以位移值相对平稳；但与此同时,随着列车向右继续运行,位于右半桥的主梁各节点位移呈缓慢增长趋势,而右半桥主梁各节点位移则正好相反,出现了远离列车的节点,位移逐渐减小的现象。而在中跨跨中附近,大约40 s以后直至停车,变形基本保持恒定,这与时间段内跨中截面附近一直处于有车状态有关。图6是轮轴竖向力单独作用下的时程情况,主梁各点的纵向位移出现了正负交替的变化规律。

图5 制动力单独作用下的主梁纵向位移时程

图6 竖向力单独作用下的主梁纵向位移时程

需要注意的是,30.80～38.56 s是动车组8节车厢共32个轮轴逐一进入线桥结构体系的时间段,由于车轮逐个进入体系,引起了线桥结构所受竖向力及制动力的变化,所以在图5和图6中上升曲线段出现了时程曲线的微小波动。通过输出车轮位置随时间的计算数据,发现38.56 s时,动车组第32个轮轴刚好进入线桥结构的左侧路基段。

图7从侧面显示了动车组共32个轮轴进入线桥结构的过程,在30.80～38.56 s时间段,线桥结构体系上的竖向力总和出现阶梯状递增,直到所有车轮完全进入线桥体系,竖向力总和才保持稳定。

图8是制动力和竖向力联合作用下,主梁一些关键位置处的纵向位移时程。从总体趋势上看,靠近停车位置处的桥梁右端位移最大,桥右侧双薄壁墩次之,中跨跨中持平。桥梁左端的位移区别于其他点,随着列车从左向右的行驶,先出现向右的正向位移,随后出现了负位移,这主要归功于列车轮轴的竖向力荷载的影响。

图7 线桥上的竖向力总和随时间的变化

图8 制动力和竖向力联合作用下的纵向位移时程

从主墩墩底弯矩时程来看,在4个薄壁墩的墩底弯矩中,左侧双薄壁墩的2个薄壁的弯矩时程几乎重合,右侧双薄壁墩也出现一样情况。值得注意的是,右侧双薄壁墩墩底弯矩是正弯矩,而左侧双薄壁墩却呈现出正负弯矩交替变化的现象,且绝对值在减少,这与桥梁左跨各节点(包括桥梁左端)的纵向位移时程变化规律相一致。时程曲线中最大弯矩出现在右侧双薄壁墩,为3 560 kN·m；左侧双薄壁墩受力较小,极值为1 000 kN·m。

按照我国《新建时速200～250公里客运专线铁路设计暂行规定》［14]“制动力采用列车竖向静活载的7%”,当列车荷载采用ZK设计活载,加载长度取用联长356 m,墩高取25 m情况下,且计算模型中主墩4个薄壁如果按平均受力考虑,则薄壁墩墩底截面由制动力引起的弯矩约为10 000 kN·m,远大于本文计算值。表明按照规范进行高速铁路制动力的计算是安全可行的,具有足够的安全储备。

7 结论

(1)由于连续刚构桥属于连续体系梁桥,除了在桥左、右端设有伸缩缝之外,主梁在桥上是连续的,正是这种连续性造成了在制动力作用下的纵向变形具有累积性。从几个关键截面的纵向水平位移看,停车时位移量最小的是桥梁左端,依次增大的是左侧主墩处、中跨跨中、右侧主墩处、桥梁右端处。其中桥梁右端主梁出现了全桥最大位移响应1.124 mm。

(2)同时,由于连续刚构桥形成的墩梁固结体系,使得全桥结构的受力和变形具有时间上的整体同步性。一旦有车轮荷载进入线桥结构,不论是桥梁左侧还是中跨跨中、或是远离列车的桥梁右端,都会发生相应大小的响应；并随着制动减速度的增加,各位置点的纵向位移几乎出现了一致的增长变形。

(3)纵向最大位移量和墩底最大弯矩并没有发生在停车瞬间,而是在制动过程中出现。因为纵向变形不但由水平作用力提供,还有竖向作用,二者的贡献量相差不多；且轮轴竖向力引起的纵向位移有交变的现象。

(4)靠近停车位置的桥梁右侧主墩出现了3～4倍于左侧主墩的弯矩,同时位移也比左墩大得多。

(5)高速列车比普通客运列车或货车的质量轻,通过计算发现,制动力和竖向力联合作用引起的全桥的纵向位移普遍较小,墩底纵向弯矩也在规范静力取值范围之内,表明动车组制动情况下连续刚构桥处于安全状态。

为了对连续刚构桥在CRH2型动车组制动力作用下的性能做进一步了解,还需要对制动力在线桥结构上的传递范围、墩高变化、停车位置、道床参数等因素的影响进行分析和计算。

［1] 雷俊卿,李宏年,冯东.铁路桥梁列车制动力的试验研究与计算分析［J].工程力学,2006,23(3):134-140.

［2] 瞿伟廉,刘嘉,涂建维,周强.天兴洲公铁两用斜拉桥主梁纵向列车制动振动反应分析［J].地震工程与工程振动,2008,28(1): 130-138.

［3] 尹京,王巍,刘鹏辉,姚京川,孟鑫.高速铁路大跨度预应力混凝土连续梁动力性能试验研究［J].铁道建筑,2012(4):6-9.

［4] 程潜,张楠,夏禾,张田.考虑制动条件的高速列车-轨道-桥梁系统动力响应分析［J].中国铁道科学,2013,34(1):8-14.

［5] 黄胜前,杨永清.高墩大跨连续箱梁铁路桥动力性能试验研究［J].铁道标准设计,2012(12):35-39.

［6] 熊震威,谢恺泽,刘浩,王平.列车制动对刚构桥上无缝线路梁轨相对位移的影响研究［J].铁道标准设计,2013(10):10-14.

［7] 李宏年.列车制动力荷载及对桥梁作用机理的研究［D].北京:北京交通大学,2001.

［8] 中铁第四勘察设计院集团有限公司.铁路无缝线路设计规范(送审稿)［R].武汉:中铁第四勘察设计院集团有限公司,2008.

［9] 王月明.动车组制动技术［M].北京:中国铁道出版社,2012.

［10]李和平,林祜亭.高速列车基础制动系统的设计研究［J].中国铁道科学,2003,24(2):8-13.

［11]饶忠.列车制动［M].北京:中国铁道出版社,2010.

［12]赵进.动车组制动实验系统研究［D].北京:北京交通大学,2008.

［13]陈丹华,刘建村.列车制动荷载的空间离散分析及应用［J].华东交通大学学报,2005(4):34-38.

［14]中华人民共和国铁道部.铁建设［2005]140号新建时速200～250 km客运专线铁路设计暂行规定［S].北京:中国铁道出版社,2005.

Analysis on Long-sPan Continuous Rigid Frame Bridge's ResPonse to Braking Force of CRH2 EMU Train

CHEN Dan-hua,CHENG Hai-gen
(School of Civil Engineering and Architecture,East China Jiaotong University,Nanchang 330013,China)

To ascertain the performance of long-span continuous rigid frame bridge under the action of braking force of CRH2 EMU train,a finite element analysis model of track-bridge was established in this study.And then the braking force time-history of car body was calculated according to braking deceleration characteristic curve of the EMU train；also the braking force time-history of every rail nodewas programmed and calculated by the use of linear interpolation theory.Furthermore,the braking force time-history and vertical force time-history of every node on rail surface were applied to the structure,and the dynamic response was analyzed by means of finite element software Midas.Analysis results show that the longitudinal deformation of main beam has accumulative character；under the combined action of braking force and vertical force,the longitudinal displacement of continuous rigid frame bridge is generally small,and the longitudinal bending moment of the pier bottom is within the range of allowable static values which are stipulated in bridge standard code.All this suggests that the continuous rigid frame bridge is in a safe condition under the action of braking force of EMU train.

high-speed train；braking；continuous rigid frame；dynamic analysis

U448.13；U448.23

A

10.13238/j.issn.1004-2954.2014.07.018

1004-2954(2014)07-0075-05

2013-09-26；

2013-10-26

国家自然科学基金资助项目(51368018)；江西省教育厅资助项目(GJJ13324)

陈丹华(1973―),女,副教授,工学硕士,E-mail:chendh73@ 126.com。