桥梁参数对桥上无缝线路伸缩力的影响分析

蔡敦锦，颜 乐，李 悦，宋彦辰，王 平

(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

桥梁参数对桥上无缝线路伸缩力的影响分析

蔡敦锦，颜 乐，李 悦，宋彦辰，王 平

(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

基于有限单元法和梁轨相互作用理论，以铁路常见桥型连续梁桥和简支梁桥为例，建立了线-桥-墩一体化桥上无缝线路计算模型，分析了伸缩力的作用规律及桥梁跨数、支座、墩台纵向水平刚度、桥梁跨度对伸缩力的影响。结果表明：宜增大连续梁相邻简支梁桥墩的纵向水平刚度，以提高其承载能力；对于多达数十跨、数百跨的简支梁，可只取10跨计算；对于多联连续梁桥，可只取相邻5跨简支梁进行计算；我国桥上无缝线路计算中一般未考虑活动支座摩擦系数的影响及将支座视为刚性体，都是偏于安全的；桥梁墩台纵向水平刚度不宜过大。

桥上无缝线路；伸缩力；桥梁跨数；墩台刚度；桥梁跨度

桥上无缝线路不同于路基上的无缝线路,因涉及到桥梁与轨道的相互作用,其研究难度较路基上无缝线路更大,随着高速铁路大规模的建设,特别是既有繁忙干线大范围换铺跨区间无缝线路及新建铁路全面一次铺设跨区间无缝线路,推动桥上无缝线路技术在近些年得到了突飞猛进的发展,极大地丰富了桥上无缝线路的技术内涵［14]。影响有作轨道桥上无缝线路梁轨纵向相互作用规律的因素很多,国内外的学者对桥上无缝线路此方面的研究已相当成熟［58],但是尚未从桥梁的角度出发,全面总结桥梁的各种参数对桥上无缝线路的影响,因此有必要对其进行研究和总结。

连续梁桥和简支梁桥作为最普遍、应用最为广泛的桥梁类型,也是铁路桥的主要桥型,本文以简支梁、连续梁为例,基于有限单元法和梁轨相互作用理论［910],研究了桥上无缝线路伸缩力的作用规律［11],以及桥梁的几种重要参数对伸缩力的影响,为完善桥上无缝线路设计方法提供参考。

1 计算模型及参数

1.1 计算模型

采用ANSYS有限元软件,在满足工程的前提下,通过一定的简化处理,建立的线-桥-墩一体化桥上无缝线路计算模型［12]如图1所示。

图1 线桥墩一体化计算模型

1.2 计算参数

简支梁以图2(a)中的5×32 m梁为例,固定支座位于简支梁左边,梁高3.09 m,自重9 000 kN,桥台纵向水平刚度取为3 000 kN/cm·双线,桥墩纵向刚度按《铁路无缝线路设计规范》规定的最小限值,取值为400 kN/cm·双线,线路阻力按Ⅲ型混凝土枕取值。

连续梁以2×32 m简支梁+(32+48+32)m连续梁+2×32 m简支梁为例,支座布置如图2(b)所示,连续梁墩台纵向水平刚度为1 000 kN/cm·双线,线路阻力参数及桥梁日温差取值与图2(a)中的简支梁相同。

图2 简支梁与连续梁布置

2 伸缩力分布规律

当混凝土桥梁日温差取为15℃时,简支梁桥和连续梁桥上的钢轨伸缩力及墩台纵向力分布如图3所示。

图3 简支梁与连续梁钢轨及墩台纵向力

由图3(a)可知,由于固定墩在左端,桥梁向右伸缩,因此在右桥台活动支座附近钢轨承受最大附加温度压力108.2kN,左桥台附近钢轨承受最大温度拉力83.5 kN；从左至右每跨桥上,钢轨承受的附加压力逐渐增大,附加拉力逐渐减小,说明桥梁伸缩引起的梁轨相互作用向右端逐渐累积叠加。左桥台承受向左方向最大纵向力87.3 kN,而其他桥跨固定支座承受的水平力均较小,约为10 kN左右,这主要是由于其他桥跨上的梁轨位移相等点近似位于跨中,桥梁承受着轨道传递的左右方向近似相等的纵向约束力所致。

由图3(b)可知,由于连续梁左右温度跨度较大,因而在连续梁左右端活动支座附近钢轨承受的附加温度压力分别为176.7、209.2 kN,连续梁右侧温度跨度为80 m,大于左侧温度跨度64 m,导致右侧附加温度压力也大于左侧,更大于全桥为简支梁的情况。左桥台承受向左方向最大纵向力126.4 kN,而其他桥跨固定支座承受的水平力均较小,连续梁固定支座承受向左方向的纵向水平力约为32.6 kN,连续梁左侧相邻的简支梁承受向左方向的纵向水平力约为30.0 kN,远大于全桥为简支梁时中间梁跨的桥墩受力,因此宜增大连续梁相邻简支梁桥墩的纵向水平刚度,以提高其承载能力。连续梁右侧相邻简支梁承受向右方向的纵向水平力约为19.5 kN,是受到了连续梁向右伸缩作用的影响所致。

3 桥梁跨数的影响

3.1 简支梁桥梁跨数的影响

设简支梁固定支座布置与图2(a)中相同,只改变简支梁跨数,钢轨最大伸缩压力及墩台最大纵向力分布如图4所示。

图4 简支梁伸缩力随跨数的变化

由图4可知,简支梁上钢轨最大伸缩压力随跨数增加而逐渐增大,左桥台承受的纵向力则随跨数的增大而逐渐降低,但当跨数增加至一定程度后,钢轨伸缩力及墩台纵向力基本上不再变化。这主要是由于各跨简支梁均向右伸缩,带动桥上钢轨也向右伸缩,随着跨数的增加,伸缩力不断累积,致使右桥台处钢轨的伸缩压力增大,左桥台处钢轨的伸缩拉力减小,因而左桥台承受的纵向力也同时减小,考虑到线路阻力的作用,伸缩力累积传递范围有限,从图4中可以看出,当简支梁跨度达到10跨及以上时,伸缩力的累积作用几乎可以忽略,钢轨及墩台承受的纵向力几乎不变。

3.2 连续梁相邻简支梁跨数的影响

以图2(b)中连续梁为例,当连续梁左、右侧简支梁跨数增加,其他参数不变时,钢轨最大伸缩压力及墩台承受的最大纵向力分布如图5所示。

图5 连续梁伸缩力随跨数的变化

由图5可知,随着连续梁两侧简支梁跨数的增加,钢轨伸缩力及墩台纵向力均逐渐减小,当两侧简支梁达到5跨及以上时,连续梁两端的钢轨伸缩力及桥墩所受纵向力几乎不再改变,左桥台的纵向力受连续梁伸缩的影响越来越小。这主要是因为简支梁在连续梁与路基间起到了缓冲作用。

4 支座的影响

4.1 支座布置的影响

通常铺设无缝线路的桥梁支座布置遵循着以下几点原则:使桥梁的温度跨度尽可能小；使桥墩受力尽可能小；固定支座宜设置在具有较大支座反力的地方；下坡方向桥台或平坡行车前方桥台支座宜设置为固定支座；固定支座设置方向宜一致；不宜将两跨梁的固定支座设置在同一桥墩上等等。遵循以上原则,改变连续梁桥第一、二跨简支梁的支座布置如图6所示,钢轨伸缩力及墩台纵向力分布如图7所示。

图6 改变后的连续梁支座布置

图7 连续梁支座改变后伸缩力分布

由图7可知,连续梁桥左侧两跨简支梁支座布置改变后,因连续梁左侧温度跨度减小,连续梁左端钢轨伸缩压力由176.7 kN降低至138.4 kN,同时连续梁右端钢轨的伸缩压力也由209.2 kN降低至192.7 kN,这对钢轨受力是有利的；但由于连续梁两侧温度跨度相差较大,两侧纵向力不平衡,连续梁桥墩受力由32.6 kN增加至54.3 kN,同时左右桥台上均为活动支座,不承受纵向力,桥梁墩台的受力不合理。因此需通过对钢轨及桥梁的检算来综合确定支座的合理布置方式。

4.2 活动支座摩擦力的影响

测试表明:活动支座的摩擦系数在0.02～0.05,改变活动支座的摩擦系数,则简支梁桥、连续梁桥的钢轨伸缩力及伸缩位移、墩台受力的变化如表1所示。

表1 活动支座摩擦系数对桥上无缝线路的影响

由表1可知,考虑了活动支座摩擦系数后,桥梁伸缩过程中将承受反向的支座摩擦力作用,相当于约束了桥梁的伸缩,这样将使钢轨受力减小,墩台受力增大；而且活动支座摩擦系数越大,钢轨伸缩力越小,墩台纵向力越大。由于不考虑活动支座摩擦系数计算所得的钢轨伸缩力有所增大,而该伸缩力一般又是桥上无缝线路设计中的控制因素,因此我国桥上无缝线路计算中一般未考虑活动支座摩擦系数的影响,是偏于安全的。

4.3 弹性支座的影响

铁路桥梁一般采用钢支座、盆式橡胶支座等,有固定支座、单向活动支座、多向活动支座之分,为简化计算,通常认为支座本身是刚性的。假定图2中所有的支座均为水平刚度为60 000 kN/m·双线的弹性支座,其他计算参数不变,则钢轨伸缩力、墩台纵向分布如图8所示。

从图8中可见,如果桥梁支座全部是弹性支座,那么桥梁伸缩导致的累积作用不明显,简支梁每跨上钢轨伸缩力分布近似相同,最大伸缩压力约为72.1 kN,墩台最大纵向力约为35.1 kN；连续梁上钢轨伸缩力呈对称分布,最大伸缩压力约为179.4 kN,墩台最大纵向力约为52.0 kN。无论是简支梁还是连续梁,钢轨及墩台的受力均远小于刚性支座的情况,可见将支座视为刚性体进行桥上无缝线路计算也是偏于安全的。

5 墩台纵向水平刚度的影响

5.1 墩台纵向水平刚度大小的影响

仅改变墩台纵向水平刚度值的大小,简支梁及连续梁上钢轨最大伸缩压力、墩台最大纵向力变化如表2所示,其余计算参数同前。

表2 墩台纵向水平刚度对伸缩力的影响

由表2可知,随着桥梁墩台纵向水平刚度的增大,无论是简支梁还是连续梁,钢轨伸缩力、墩台纵向力均随着增大,但增加幅度在逐渐减缓。这是因为桥梁墩台纵向水平刚度越大,在钢轨反作用力下桥梁整体位移所受约束越强,梁轨位移相等点越靠近固定支座,相等点两侧的纵向阻力之和越大,致使钢轨及桥梁承受的纵向力也越大。因此,从减小钢轨伸缩力的角度考虑,桥梁墩台纵向水平刚度不宜过大。

5.2 墩台纵向水平刚度差的影响

由于地形的限制,桥梁各个墩台的高度是很难建造成一致的,因而各墩台的纵向水平刚度也不会相同,假定图2(a)中简支梁与连续梁中间跨的墩台高度大于其他梁跨的墩台高度,即中间梁跨(图2(a)中第3跨简支梁与图2(b)中连续梁固定墩)的桥墩纵向水平刚度较其他梁跨小一些,则钢轨伸缩力及墩台受力的大小如表3所示。

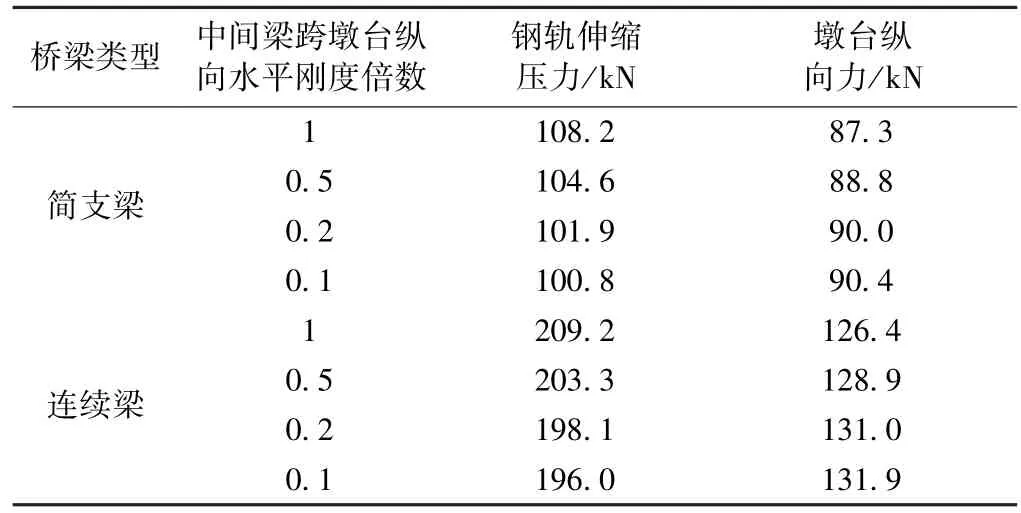
表3 墩台纵向水平刚度差对伸缩力的影响

由表3可知,中间主跨桥墩的纵向水平刚度越大,钢轨伸缩力越大,墩台受力越小,钢轨位移也越大,但变化量较小。因此,各桥墩纵向水平刚度差对伸缩力的影响很小,不作为影响钢轨伸缩力的控制因素。

6 桥梁跨度的影响

桥梁跨度对伸缩力的影响其实是温度跨度的影响,以图2中简支梁、连续梁为例,简支梁桥假设其跨度从24 m变化至64 m,连续梁桥中间跨的跨度从32 m变化至80 m,其他参数不变,钢轨最大伸缩压力及墩台所受纵向力随桥梁跨度的变化如图9所示。

从图9中可见,无论是简支梁还是连续梁,钢轨伸缩力、墩台纵向力均随桥梁跨度的增加而呈比例线性增加,说明桥梁跨度也即温度跨度是影响桥上无缝线路伸缩力较为重要的因素。当桥梁温度跨度增加至一定程度后,就需设置小阻力扣件、钢轨伸缩调节器或传力机构,以减缓钢轨及桥梁的受力。

图9 简支梁与连续梁伸缩力随跨度的变化

7 结论及建议

(1)连续梁相邻的简支梁承受的纵向水平力远大于全桥为简支梁时中间梁跨的桥墩受力,因此宜增大连续梁相邻简支梁桥墩的纵向水平刚度,以提高其承载能力。

(2)对于多达数十跨、数百跨的简支梁,为简化计算,可以只取10跨简支梁进行计算；对于多联连续梁桥,可只取相邻5跨简支梁进行计算。

(3)桥梁支座的合理布置形式,需通过对钢轨及桥梁的检算来综合确定。

(4)我国桥上无缝线路计算中一般未考虑活动支座摩擦系数的影响,将支座视为刚性体都是偏于安全的。

(5)从减小钢轨、桥墩受力的角度考虑,桥梁墩台纵向水平刚度不宜过大。

(6)当桥梁温度跨度增加至一定程度后,就需设置小阻力扣件、钢轨伸缩调节器等,以减缓钢轨及桥梁的受力。

［1] 广钟岩,高慧安.铁路无缝线路［M].北京:中国铁道出版社,2005.

［2] 蔡成标.高速铁路特大桥上无缝线路纵向附加力计算［J].西南交通大学学报,2003(5):609-614.

［3] 唐乐,陈秀方,朱文珍.连续梁桥上无缝线路伸缩附加力计算研究［J].铁道科学与工程学报,2005(4):35-61.

［4] 魏贤奎,王平,徐浩,陈嵘,肖杰灵.铁路上承式拱桥上无缝线路断缝影响因素［J].中南大学学报,2013(7):3053-3060.

［5] 闫斌,戴公连.高速铁路斜拉桥上无缝线路纵向力研究［J].铁道学报,2012(3):83-87.

［6] RUGE P,BIRK C.Longitudinal Track-bridge Interaction due to sudden Change of Coupling Interface［J].Computers&Structures, 2007,85(7-8):458-475.

［7] BATTINI J M,MAHIR U K.A Simple Finite Element to Consider the Non-linear Influence of the Ballast on Vibrations of Railway Bridges［J].Engineering Structures,2011,33(9):2597-2602.

［8] 戴公连,闫斌.高速铁路斜拉桥与无缝线路相互作用研究［J].土木工程学报,2013(8):90-97.

［9] 徐庆元,陈秀方,李树德.高速铁路桥上无缝线路纵向附加力研究［J].中国铁道科学,2006(5):8-12.

［10]Ladislav FRYBA.无缝线路与铁路桥梁温度力的相互作用［J].铁道标准设计,1987(4):46-54.

［11]谢恺泽,徐井芒,魏贤奎,王平.桥上无缝线路附加伸缩力放散的计算研究［J].铁道标准设计,2012(4):28-30.

［12]魏贤奎,陈小平,王平.有作轨道基础桥上无缝线路计算软件开发与应用［J].铁道建筑,2010(8):115-118.

Analysis on How Bridge Parameters Affect the ExPansion and Contraction Force of Continuous Welded Rail on Bridge

CAI Dun-jin,YAN Le,LI Yue,SONG Yan-chen,WANG Ping
(Ministry of Education's Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University,Chengdu 610031,China)

In this study,based on the finite element method and the theory of interaction between girder and rail,the commonly used bridge types,which include continuous girder bridges and simply-supported girder bridges,were cited as the examples.Subsequently,an integrated track-bridge-piers calculation model of continuous welded rail on bridge was established；the expansion and contraction force characteristics was analyzed；and the influences upon the expansion and contraction force caused by the number of bridge spans,by bridge bearing,by longitudinal horizontal rigidity of pier and abutment,and by bridge span length,were researched.The result shows that:(a)It is necessary to increase the longitudinal horizontal rigidity of the pier of the simply-supported girder adjacent to the continuous girder of the bridge,so as to increase this pier's bearing capacity.(b)The simply-supported girder bridge, which is made of tens to hundreds of spans,can be calculated by only taking its ten spans.(c)The multi-unit continuous girder bridge can be calculated by only taking five adjacent simply-supported girders.(d)In China,the continuous welded rail on bridge is calculated generally without considering the effect of friction coefficient of movable bearing and the bearing is regarded as a rigid body.Those practices are on the safe side.(e)The longitudinal horizontal rigidity of bridge pier and abutment should not be designed too large.

continuous welded rail on bridge；expansion and contraction force；the number of bridge spans；rigidity of pier and abutment；bridge span length

U213.9

A

10.13238/j.issn.1004-2954.2014.07.007

1004-2954(2014)07-0030-05

2013-10-23；

2013-10-30

中央高校基本科研业务费专项资金资助项目(编号: 2682013CX043)

蔡敦锦(1989―),男,硕士研究生,E-mail:1198876623@ qq.com。