基于竞争风险模型的居民活动-出行计划研究

吴文静，罗清玉，贾洪飞

（吉林大学 交通学院，长春130022）

基于竞争风险模型的居民活动-出行计划研究

吴文静，罗清玉*，贾洪飞

（吉林大学 交通学院，长春130022）

对出行者活动-出行计划行为的研究有助于进一步解析出行者的行为决策机理，也是制定和实施交通管理政策的前提.本文扩展了传统的基于单一删失事件的生存风险研究，将竞争风险模型应用于出行者活动时间分配行为的研究，基于吉林市居民出行数据的分析，提取出行者制定活动计划的影响因素，通过敏感性分析，解析出行者在连续时间轴上活动参与类型与活动持续时间的联合选择过程.结果表明：出行者N次与N+1次活动之间存在相互联系、相互制约关系，且关系强度又随着参与活动类型的不同而存在显著差异，竞争风险模型能有效应用于这些差异性的分析，丰富和扩展了出行行为的分析理论与方法.

城市交通；活动-出行行为；竞争风险模型；时间分配；出行者

1 引 言

交通需求管理和控制与时间因素密切相关，出行者的时间分配模式与其日活动计划、出行安排存在相互制约关系，是出行行为分析的核心内容.随着社会经济的发展，居民的生活范围逐渐扩大，除了上班、上学等刚性需求外，人们往往会根据自己的需要和喜好在一天中的其他时段内安排长度不等、数量有限的弹性需求活动，例如购物、聚餐、休闲健身等，并利用出行从空间和时间上将这些分散的活动连接起来.人们的时间分配模式将直接影响其活动类型、出行次数、目的地选择等行为决策.本文的研究将探讨出行者的时间分配模式与其自身的社会经济属性及交通系统之间的相关性，解析出行者的时间分配过程、活动安排，从而为预测出行者的出行需求提供参考，为制定和实施交通管理政策、引导人们的出行需求提供依据.

在对时间安排的行为建模中，最为常见的是持续时间分析模型.持续时间分析模型分析事件在已持续时间的影响下结束时刻的条件概率，引入时间依赖性的概念，建立事件结束概率与已持续时间之间的数量关系，能描述事件发生的动态过程.它主要应用于生物学和医学，用于评估和预测生物和人的生存时间.目前，持续时间分析模型已广泛应用于出行者活动开始时间、活动持续时间等行为的分析，例如Hamed&Mannering和Bhat研究了通勤者工作结束后所参与的非工作活动的出发时间选择行为[1，2]；Abu-Eisheh&Mannering研究了上班出发时间[3]；Mannering&Hamed研究了出行者为避开高峰时段而选择的通勤时间[4]；Andersen等对生存风险模型与方法的优缺点进行了讨论[5]；吴文静运用加速失效模型研究非通勤者活动-出行时间选择行为[6].但是，从现有的研究来看，这些模型都没有考虑到各项活动在时间维中存在的竞争关系.从活动的时空消耗特性来看，除刚性需求活动外，出行者参与的其他活动类型之间、在家（单位）活动和外出活动之间都普遍存在着替代效应，例如若安排给工作的时间多了，那么娱乐的时间就会减少；在有限的时间内，人们会在购物与休闲娱乐活动之间选择.而传统的风险持续模型都无法体现这些活动之间的替代和竞争关系.

因此，本文将扩展持续时间分析模型在出行行为中的应用，引入竞争风险模型用于分析出行者活动-出行的时间分配行为，分析出行者时间安排的外部影响因素，并探讨出行者各项活动之间的竞争关系.

2 竞争风险模型

传统的持续时间分析研究仅关心某一个终点的情况，然而在实际问题中，观察的终点往往不是单一的，而是存在多个终点和竞争风险.比如失业者找到工作或者退出劳动力市场都会导致失业状态结束，引起贷款抵押终止的原因可能是贷款者提前还贷也可能是违约.因此，若在可能会发生多个终点事件的情况下仍应用单终点分析方法，将会由于竞争风险的存在而导致对这些终点事件概率的估计偏差.同时，由于同一观察对象的不同终点之间存在相关，因此也不宜采用多次单一终点的持续时间分析方法进行分析.此时对事件终止概率的研究需要考虑不同的原因，也即不同的风险，这就是竞争风险模型（competing risks）.目前这一模型已成为处理具有多重原因的经济持续数据的重要方法.基于Cox的竞争风险模型的模型基本表达式为

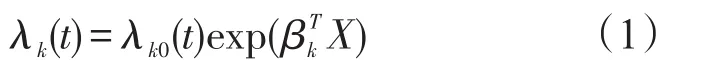
式中 λk(t)表示协变量X在时间t上发生第k种终点事件的风险率；λk0(t)表示第k种终点事件在时间t上的基础风险率；βk是协变量X的系数向量.其联合生存函数为

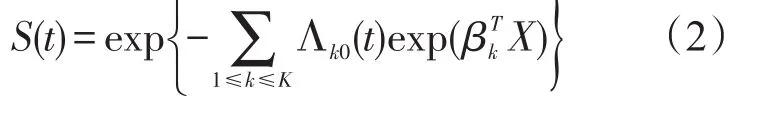
式中 Λk0(t)表示累积基础风险函数；K为导致事件终止的风险类型的集合.此时第n个观察的第k种风险事故发生的概率为Pkn，则其风险概率为

协变量参数的部分似然函数为

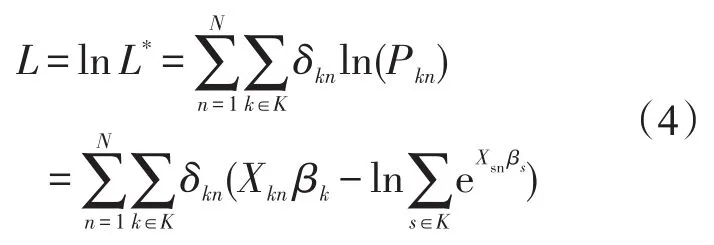
式中 δkn表示第n个观察的第k种风险的指示变量.令 dL∕dβ=0，使用最大似然法的Newton-Raphson进行迭代，得到估计参数β.由协变量估计的似然函数结构可知，其参数的估计与MNL模型相类似，因此可以借鉴MNL模型的参数估计方法即极大似然估计方法应用于此模型的研究，分析协变量对应变量的影响.

3 竞争风险模型在出行者的活动计划行为中的应用

将上述对出行行为的分析与竞争风险模型相联系，可将出行者一系列活动链中相邻两项活动的计划与时间安排作为分析对象.出行者某次活动结束有多种可能，例如某个人上班结束后，可能会直接回家，那么他一天的活动就此结束，成为删失事件；但也可能去购物或是聚会，此时活动结束就存在多种结果，即互为竞争风险事件.在此，我们把出行者完成了某次活动（N次活动）后的继续活动（N+1次活动）作为我们的观测事件，分析出行者N+1次活动的安排.其中，N+1次活动根据其类型可以划分为上班(k=1)、购物(k=2)、娱乐休闲（k=3）、个人事务（k=4）四种竞争类型，而活动结束打算回家作为删失(k=0).

此外，由分析可知出行者N+1次活动的安排受到多种因素的影响，例如N活动的持续时间、N+1次活动的预算时间等，具体来说可分为以下几种类型：

（1）出行时间：基于聚集效益理论，通常出行者对某些活动地点的选择与到达该地点所花费的出行时间成反比.因此，例如出行者到达某地点进行娱乐活动所需花费的出行时间越长，那么出行者到达该地点活动的可能性就越小.

（2）出行方式：相比于轨道交通、公交车等公共方式，出租车、私家车具有较大的机动性和灵活性，因此私家车主的活动范围及活动计划相对而言更为复杂.

（3）活动的开始时间：N+1次活动开始时间会影响N次活动的持续时间.例如某人上班时间提前，因此在家至单位之间的预算时间减少，从而会影响在上班开始前的某一次活动的进行.

（4）活动结束时间：N次活动的结束时间同样也会影响到N+1次活动的开始，例如某人的下班时间提前，那么可能在下班途中会增加一次购物出行.

（5）出行者特征：出行者的性别、年龄、收入等属性会影响到出行者的行为偏好与价值取向，从而影响到出行者活动计划的制定.

4 案例分析

4.1 样本数据分析

（1）活动链计划.

应用某年吉林市居民出行数据，基于活动链分析，统计出行者的活动计划行为.每一次出行都存在着与之相关联的下一次出行.通过统计，出行者的活动链计划如表1所示.

表1 出行者活动-出行计划表Table 1 Activity travel schedule of travelers

由此可见，吉林市居民大部分的活动都在家与单位之间往返，当然也包括上下班途中的购物与娱乐休闲活动.

（2）活动持续时间.

基于stata软件的Kaplan-Meier分析对观测事件进行样本分析，对活动计划还未结束的某次活动的持续时间进行估计，结果如图1所示.

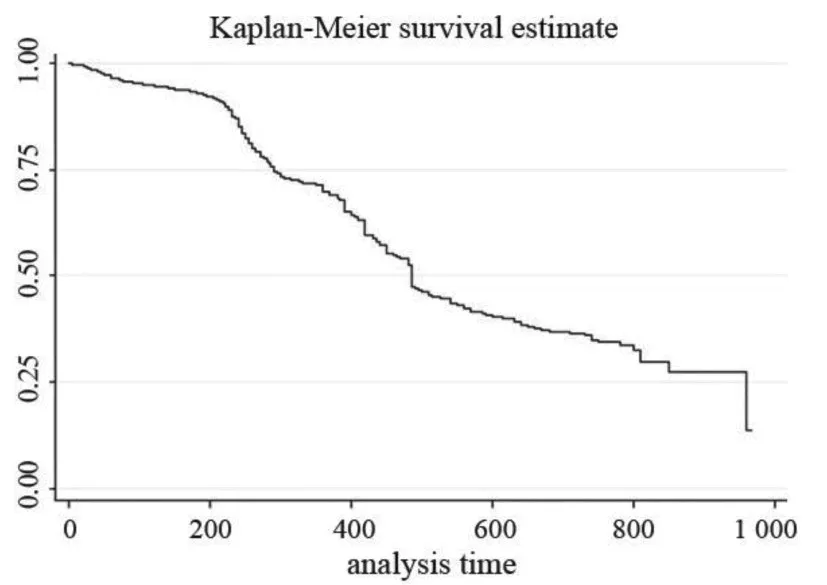
图1 活动持续时间的生存曲线Fig.1 Survey curve of activity duration time

通过检验，其形状参数P为1.71＞1，因此可以判断活动时间服从weibull分布，并且可以用威布尔回归来进行分析.

4.2 基于weibull模型的协变量参数估计与结果分析

对竞争风险模型的协变量中的参数进行估计，结果表明在第3节中所列出的影响因素中，其中出行者的年龄(age)、收入水平(salary)、至N+1个地点的出行时间（traveltime）以及N次活动的结束时间(endtime)对出行者活动的持续时间存在显著影响，结果如表2所示.其中，对不同类型的样本数据分布进行估计，见形状参数F值，系数β表示每增加一个单位，风险度改变多少倍.

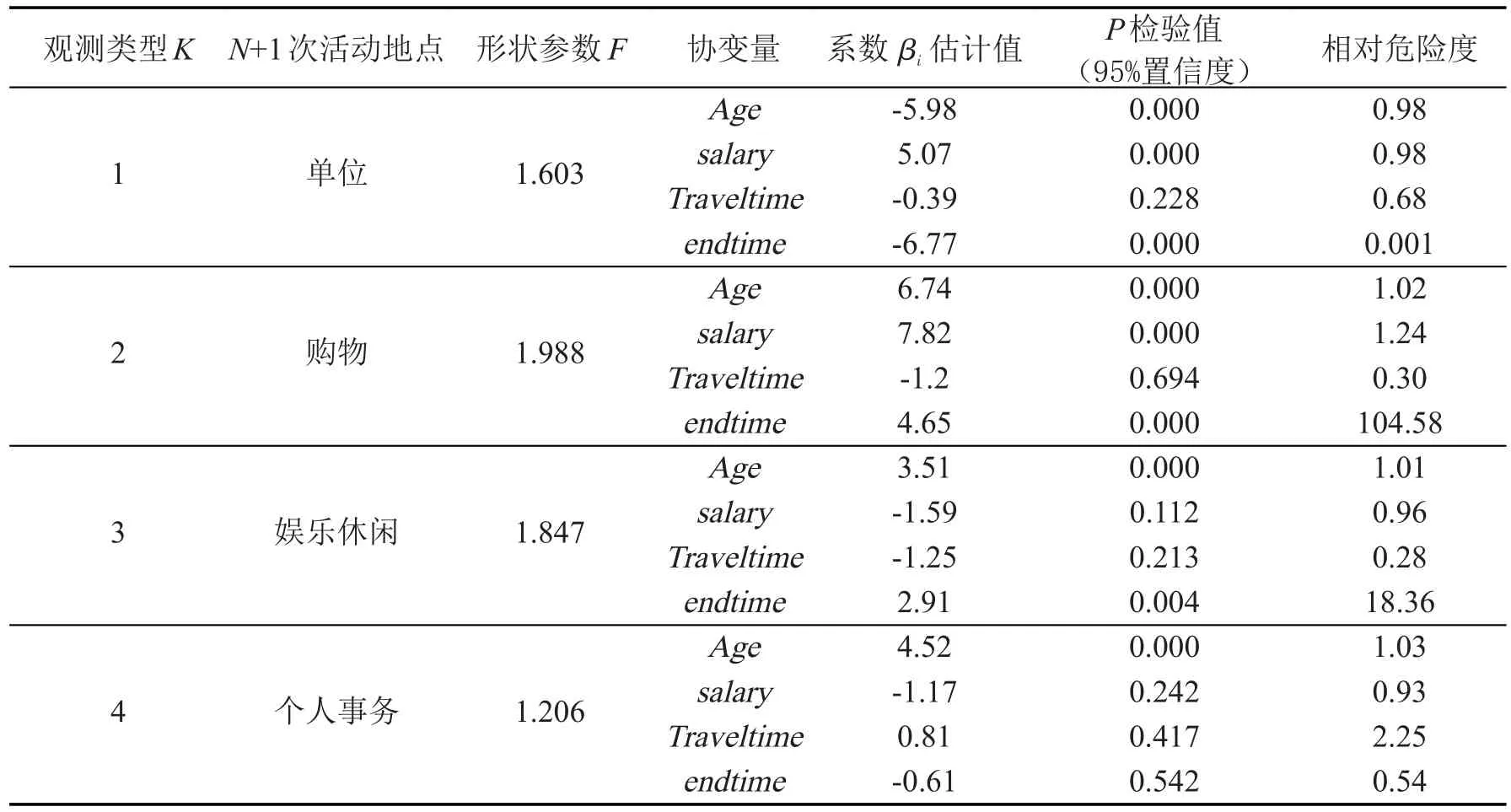
表2 基于weibull分布的模型参数估计结果Table 2 Estimation result of parameters based on weibull model

由此可见：

（1）除了至单位活动外，其他类型活动的相对危险度都随着年龄的增加而增加，表明年龄越大，至单位的活动就越重要，出行者会压缩去单位前的活动而保证上班活动的正常.从收入水平来看，高收入水平的居民上班前的活动时间较少，而购物活动开始前的活动持续时间较长.而低收入者的购物活动往往穿插在多次活动的间歇进行，因此购物活动开始的前一次活动持续时间较短.

（2）出行时间的持续时间是包含在N次活动的持续时间内的，因此出行时间越长，N次活动的可利用时间就越短，反过来，如果N+1次活动是刚性需求，那么出行时间越长，N次活动就会被压缩，甚至取消.由结果可知，出行时间影响下，至单位、购物、娱乐活动开始前的活动持续时间都受到了影响，其中至单位的影响最为显著，随着出行时间的增加，出行者上班前的活动参与的风险率增加了68%，其次受到影响的是购物与娱乐活动.而由结果可知，随着出行时间的增加，处理个人事物前的活动反而也延长了，可能是由于居民如果要去距离比较远的地方办理事务，通常会在完成必要的一些工作之后再进行.

（3）endtime反映的是N次驻停活动的结束时间，由结果可知，N次活动的结束时间对居民N+1次上班活动的影响并不太显著，可能在上班前居民的活动范围并不是太广，且通常会保证上班活动正常进行.影响最为显著的是购物与娱乐休闲，结果表明，结束时间每推迟一个单位，风险度变化的幅度急剧上升，甚至超过100%，结合数据分析，吉林市居民的购物与休闲活动主要集中在早晨与晚上，因此如果早晨的可利用时间不够，很多居民会将购物与休闲活动转移到晚上.

4.3 基于极大似然估计的模型参数估计结果分析

基于式（5）在此借鉴MNL模型的参数估计方法对参数β进行估计，如表3所示，并分析各影响因素对出行者活动计划影响的敏感性，其中将k=0作为参照项，Aim变量表示出行者N次活动的类型，Aim1为上班、上学；Aim2为购物；Aim3为娱乐活动；Aim4为个人事物.

表3 基于极大似然估计的模型参数估计结果Table 3 Estimation result of parameters based on MLE model

由结果可知：

（1）若下一次活动为去单位上班（K=1），那么出行者的上一次活动可能是购物、休闲或者也是上班，且从系数的正负表明，购物活动后出行者去单位的概率减少，而在上班前相比于购物与上班活动，出行者更有可能参与的是休闲娱乐活动.

（2）若下一活动为购物（K=2），结果表明出行者在休闲娱乐过后最愿意去购物，而且相比于个人事物，在上班之后进行购物的概率最小.

（3）若下一活动为休闲娱乐（K=3），那么表明出行者的休闲娱乐活动发生在购物之后的概率比发生在上班之后的可能性更大.

（4）若下一次活动为处理个人事物（K=4），那么表明此次活动更容易发生在购物之后.

4.4 模型比较及结果分析

本文分别选择了服从weibull分布的参数估计方法与极大似然估计方法对竞争风险模型的参数进行估计和比较两类模型.

（1）基于weibull分布的参数估计模型是研究某一种类型，其生存状况参照于所有其他非此类的删失样本的情况下的分析结果.例如分析k=1类，其删失样本为（k=0及k＞1）.而基于极大似然估计的参数估计模型是相比于参照项，即出行者已完成活动计划的情况下，即k=0的情况下的分析结果.

（2）由于模型估计方法的差异性，两类模型分析的影响因素不同，前者分析了某一因素对出行者某次活动的持续时间的影响，而后者反映了某一因素对某次活动发生情况的影响.

5 研究结论

出行者的时间分配模式、活动计划在交通需求管理策略和交通控制措施的制定和评价中越来越受到重视.尤其对于通勤者在上下班高峰时期的活动链选择行为的研究，有助于交通管理部门采取相应措施有效引导出行者的出行行为，对于缓解高峰时期的交通压力具有实际意义.本文扩展了传统的基于单一删失事件的生存风险研究，将生存分析中的竞争风险模型应用于出行行为的研究，不仅可以分析出行者的时间选择行为，也可分析出行者的活动计划.本文模型方法还存在着一些需要进一步研究的地方：

（1）因为吉林市的经济发展原因，导致模型结果存在一定偏差，一是出行者参与购物、娱乐等活动的样本量并不是很多，因此影响了对这一出行行为的分析结果的准确性;二是购物、娱乐等活动的时间分布与上班等活动的时间分布的差异性不够明显.

（2）应探讨行为分析结果与需求管理政策的结合，如何根据模型结果调节出行需求，从而缓解现实中存在的交通问题是需要进一步研究的内容.

[1] Bhat, et al. A comprehensive econometric microsimulator for daily activity-travel patterns[J]. Transportation Research Record,2004,1894:57-66.

[2] Hamed M M,Mannering F L.Modeling travelers’postwork activity involvement:toward a new methodology[J]. Transportation Scicence, 1993,27: 381-394.

[3] Abu-Eisheh S A,Mannering F L.Discrete∕Continuous analysis of commuters’route and departure time choices[J].Transportation Research Record,1989,1138: 27-34.

[4] Mannering, Hamed. Occurrence, frequency, and duration ofcommuters’ work-to-home departure delay[J].Transportation Research B,1990,24(2):99-109.

[5] Andersen P K,Geskus R B,de Witte T,et al.Competing risksin epidemiology:possibilitiesand pitfalls[J]. International Journal of Epidemiology,2012.

[6] WU Wen-jing,JUAN Zhi-cai,GAO Jing-xin,et al. Research on time-choosing behaviors of travelers based on AFT model[C]∕1st International Conference on Sustainable Construction and Risk Management,2010: 1050-1055.

Activity-travel Schedule Planning Based on Competing Risk Hazard Model

WU Wen-jing,LUO Qing-yu,JIAHong-fei
(Transportation College,Jilin University,Changchun 130022,China)

The study of the schedule planning of travelers helps to understand the process of travelers’decisions.Also it is the premise of enacting and implementing traffic management strategy and policy.A competing risk hazard model,which describes simultaneously the duration of the present activity and the choice of the next activity,is presented.The application of the model extended to the field of traditional hazard models which account for only one delete events.The model is estimated based on the survey data of Jilin City,China.The covariates used in the model represent factors that affect activity scheduling.The estimated model suggesting that there is interrelated and constraint relationship between N and N+1 times activities of travelers,Moreover,the strength of that relations are change significantly with type of activities. The competing risk models used in this paper are a useful tool for describing such differences.These fundamental works is help for enriching and expanding the travel behavior analysis theory and method.

urban traffic;activity-travel behavior;competing risk hazard model;time allocation;travelers

2014-06-23

2014-10-15录用日期：2014-10-22

国家自然科学基金项目（51278221）；博士后科学基金（2013M541307）.

吴文静（1980-），女，江苏省苏州市人，博士，讲师. *

luoqy@jlu.edu.cn

1009-6744（2014）06-0171-05

U491

A