基于时间剩余的随机后悔最小化路径选择

李梦甜，纪翔峰，张 健，冉 斌*

（1.东南大学 城市智能交通江苏省重点实验室，南京210096；2.现代城市交通技术江苏高校协同创新中心，南京210096）

基于时间剩余的随机后悔最小化路径选择

李梦甜1,2，纪翔峰1,2，张 健1,2，冉 斌*1,2

（1.东南大学 城市智能交通江苏省重点实验室，南京210096；2.现代城市交通技术江苏高校协同创新中心，南京210096）

出行者路径选择行为的正确性直接影响到交通规划“四阶段”模型最后一步交通分配的可靠性，对交通规划领域具有重要意义.近年来，为了克服出行者路径选择主要理论（随机效用最大化模型）存在的问题，Chorus提出了随机后悔最小化模型.本文借用经济学领域中的无差异曲线概念，建立基于时间剩余的出行时间和出行费用双重约束下的随机后悔最小化模型，并对模型中存在的路径重叠和路径感知方差问题进行改进.最后运用示例性路网进行数值检验.结果显示，改进模型更加合理，具有更好的可靠性.

交通工程；路径选择；双约束随机后悔模型；时间剩余；无差异曲线；路径重叠；路径感知方差

1 引 言

构建出行者的路径选择模型，对城市交通系统的分析具有重要的理论价值和实践意义，其结论的科学性直接影响到交通分配模型的可靠性.路径选择模型是否能够真实地反映出行者的选择行为，主要取决于选择模型的行为假设.从七十年代中期以来，基于随机效用最大化（Random utility model,RUM）假设的离散选择模型是研究出行者随机选择行为的主要模型[1-3].该模型假设当出行者面对一系列的出行选择时，倾向于选择效用最大的路径.目前，RUM模型不仅已经成功地应用到了交通规划的科学研究中，而且很多商业仿真软件(例如TransCad)也基于RUM模型进行了有效开发.

尽管RUM模型取得了众多的成果，在研究的过程中，研究者也发现RUM模型存在的一系列问题.首先，模型假设出行者是完全理性的，这对于出行者提出了极高的要求，基本无法实现；其次，最初的RUM模型存在无法克服的IIA特性（Independence of irrelevant alternatives，IIA）.很多研究者很早就观察到了这一特性并对模型进行了一系列的改进[4,5]，但是结果仍然不如人意.随着行为科学的发展，国内外研究者[6-9]考虑到出行者的有限理性，类比RUM模型，Chorus在2008年引入基于后悔最小化理论的理性选择模型（Random regret model, RRM）[9]进行路径选择行为刻画.

RRM模型的行为假设基于后悔最小化，同时考虑了后悔值没有完全覆盖的随机因素.当一个出行者必须在多个选择方案的多个属性之间进行权衡时，如果一个未选择方案的一个或者几个属性的效用优于已选择方案，就会产生后悔.相比于RUM模型，RRM模型关于未选择方案后悔值最小化的理论更能刻画出行者的选择心理和行为.此外，RRM模型还能够有效地克服IIA特性[10-12].

无差异曲线是西方经济学中的一个概念，JudithWang[13]在文献中创新性地将该概念引入到出行者的路径选择模型中.本文将进一步将基于无差异曲线的时间剩余概念和随机后悔最小化模型联系起来，并改进RRM模型存在的路径重叠和路径感知方差问题，建立改进的基于时间剩余的出行时间和出行费用双重约束下的随机后悔最小化模型，并对模型存在的两个问题进行修正和算例验证.最后，本文运用示例性路网进行数值检验，并与基于时间剩余的RUM模型进行了对比，验证模型的可靠性.

2 无差异曲线及时间剩余

无差异曲线（Indifference curve）是指在一定的条件下，消费者为了获得相同的满意度，增加一种商品的消费必须减少另外一种商品，不能同时增加或减少.将无差异曲线应用到出行时间和出行费用双重约束的交通网络上，出行时间和出行费用可组成一条无差异曲线.即在交通网络中，如果出行者希望花费更少的时间，那么他必将愿意支付更高的费用.图1为基于出行时间和出行费用的无差异曲线的示例，无差异曲线在本文表示出行费用和出行者愿意花费的出行时间之间的函数关系，是定义时间剩余的基础.

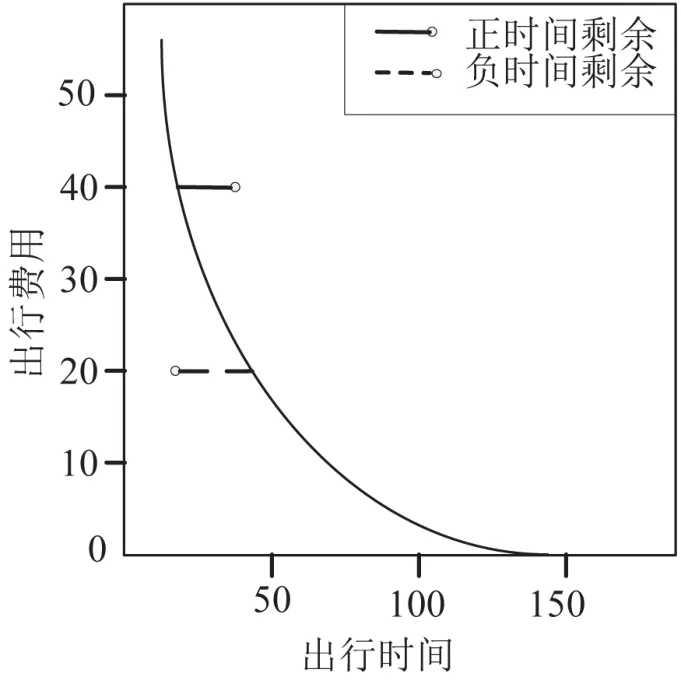
图1 基于出行时间和出行费用的无差异曲线Fig.1 An indifference curves between time and roll

本文引用文献[10]提出的时间剩余的概念，即出行者愿意花费的出行时间减去出行者实际花费的出行时间.在出行时间和出行费用双重约束的交通路网中，出行者愿意花费的出行时间是通过无差异曲线这一函数关系由出行费用转化得到.根据定义，容易发现出行者更愿意选择时间剩余大的路径.时间剩余有正负之分，正时间剩余可以理解为出行者愿意选择某条路径，而负时间剩余可以视为一条不受欢迎的路径.但是，文献[13]只考虑了正时间剩余，默认若出现了负时间剩余，出行者不会出行.然而，如果出行者既不愿意支付费用，又不愿意花费更多的出行时间，对于该出行者而言，所有的有效路径都是负时间剩余，但是出行仍然是存在的.为了克服这个问题，本文采用了随机后悔最小化模型来描述时间剩余，将负时间剩余定义为正后悔值，而将正时间剩余定义为负后悔值.

假设出行时间和出行费用的无差异曲线方程为 f(x)，则对于起点O和终点D之间的OD对，设fa、τa、ta分别为路段a的流量、收费和出行时间，得到路径i的时间剩余TSi的表达式为

则考虑随机因素影响的后悔值Ri的表达式为

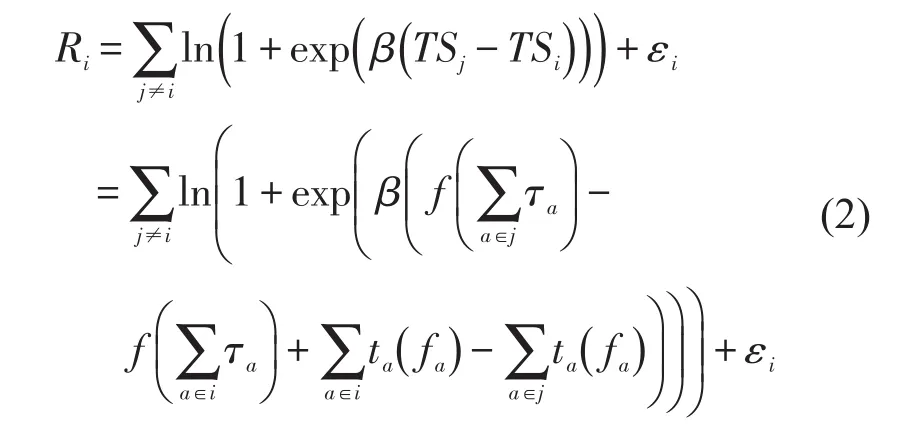
式中 εi——随机误差；

β——时间剩余差值的估计参数.

式（2）中，后悔值表示的是两条路径的时间剩余差值的演化形式，其中时间剩余的差值就是TSj-TSi，路径i表示的是基准路径（也就是选择的路径），路径 j表示非基准路径（也就是与所选择路径进行对比的路径），而上述演化形式参考了Chorus[7，9-11]的一系列研究成果.

3 模型建立

3.1 RRM模型

随机后悔最小化模型的关键概念是当出行者在所有的备选方案中进行选择时，他会将当前方案与其它方案的每个特征属性一一对比，尽量避免其它方案的特征属性由于当前方案的特征属性而导致的后悔.在本文中不同路径的特征属性为时间剩余.

假设随机误差εi服从Gumbel分布，则选择集C中路径i的选择概率Pi计算如式（3）所示.

3.2 路径重叠和基于效用改进参数的RRM模型

尽管RRM模型不像MNL模型那样受IIA特性制约，但是仍存在一定缺陷，路径重叠即为其中之一，即RRM模型在计算相关联路段情况时结果不准确.为了克服这一缺点，较为常用的方法是在概率函数的指数表达式中引入效用改进参数，计算如式（4）所示.

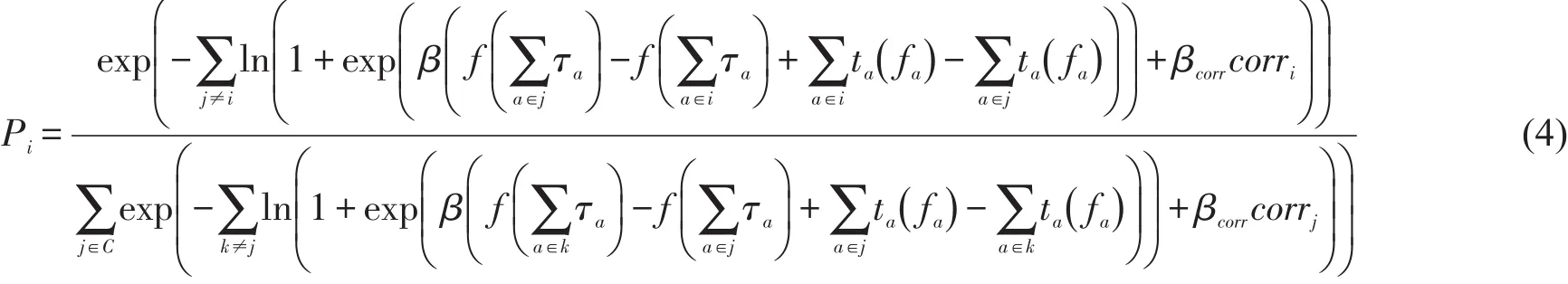
式中 corri——效用改进参数；

βcorr——效用改进参数的估计参数.

效用改进参数corri引用共同项来表达重叠程度，其中“长度”定义为路径无关的花费（例如物理长度或者自由流旅行时间）.

式中 Li——路径i的长度；

Lj——路径 j的长度；

Lij——路径i和 j的重叠长度.

3.3 路径感知方差和基于位置的RRM模型

传统的RRM模型不能够解释不同路径间的感知方差.如图2所示的两个具有两条路径的交通网络，两条路径间的时间剩余差均为5.但是，图2（a）中的长路径时间剩余是短路径时间剩余的两倍，而图2（b）中的长路径时间剩余仅仅比短路径时间剩余大4%.

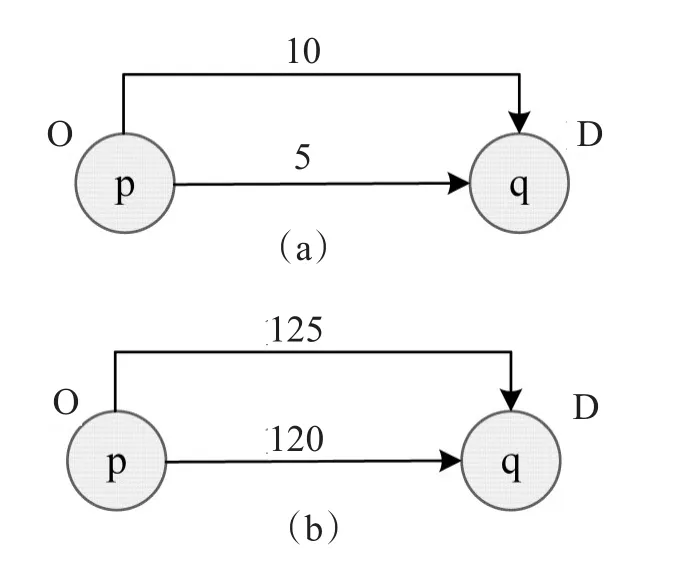
图2 不同路径感知方差的双路径交通网络图Fig.2 Two route network for different perception variance

采用传统的RRM模型，可得图2两种情况下的长路径选择概率分别为：

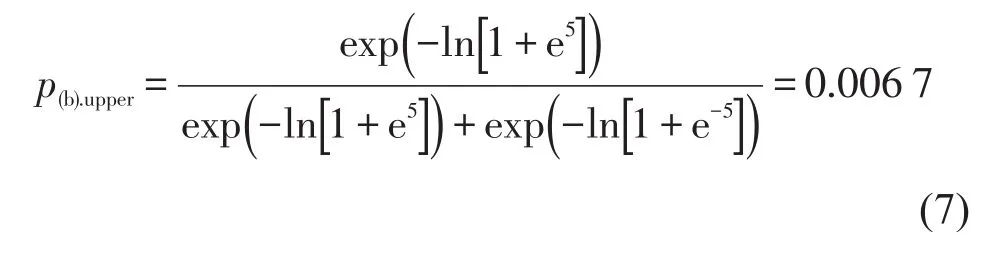
但是，在实际的出行选择行为中，对于图2（a）的网络，采用传统的RRM模型计算出的结果大致正确，而对于图2（b）的网络，由于路径时间剩余的基值比较大，因此两条路径间的时间剩余差值体现得不明显，在实际选择过程中两条路径的选择概率并没有太大差距，因此采用传统的RRM模型在这一问题上的结果并不能完全的反映现实情况.

针对这一问题，本文采用基于位置的RRM模型来研究基于时间剩余的路径感知方差问题，该模型是基于我们已有的研究成果[14]，计算如式（8）所示.

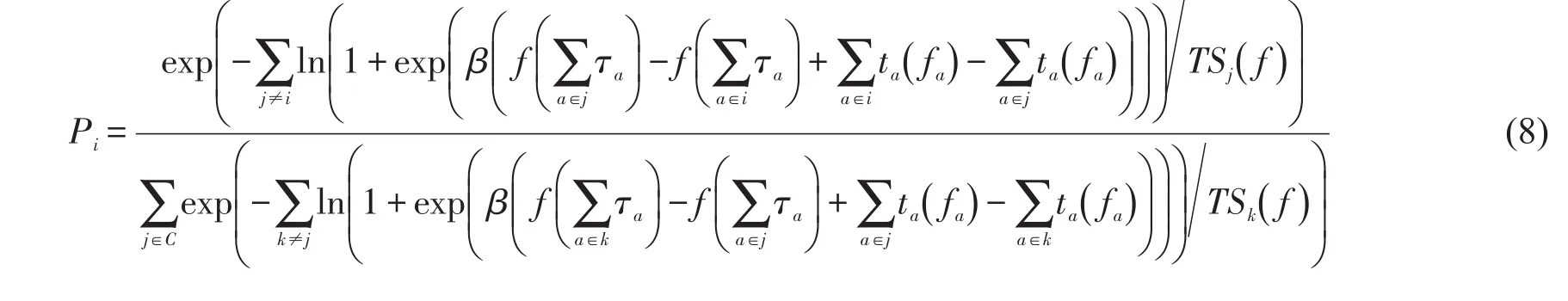
3.4 改进的基于时间剩余的随机后悔最小化模型

综合3.2节和3.3节，得到改进的基于时间剩余的随机后悔最小化模型为

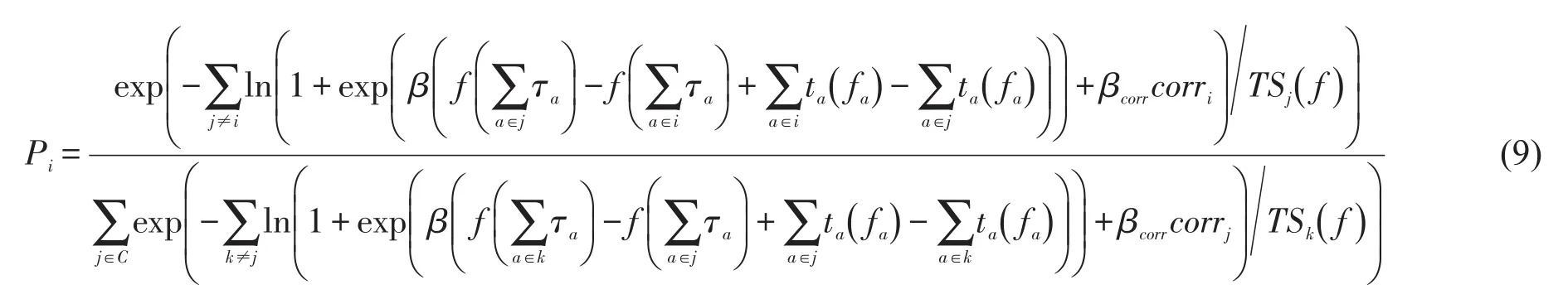
4 数值检验

本文采用图3所示的“loop-hole”网络[15]来检验基于效用改进参数的RRM模型.如图3所示，这个交通网络有三条路径，路径1和路径2有一段重叠路径，路径3为独立路径.

假设每条路径的费用为10，出行时间为100，重叠路径的长度为x，x的取值范围为0到100之间.令 β=βcorr=1，根据式(3)和式(9)，计算得到RRM模型和RRM-CF模型的独立路径选择概率如图4所示.

图3 “loop-hole”网络Fig.3 Loop-hole network

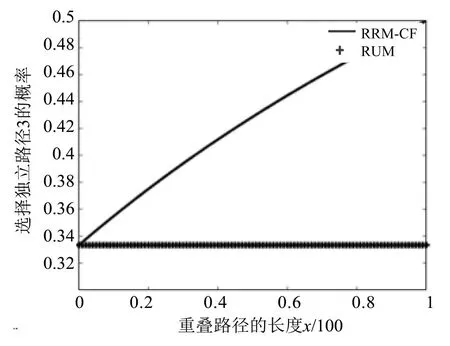
图4 RRM模型和RRM-CF模型独立路径选择概率Fig.4 Probability of choosing route 3

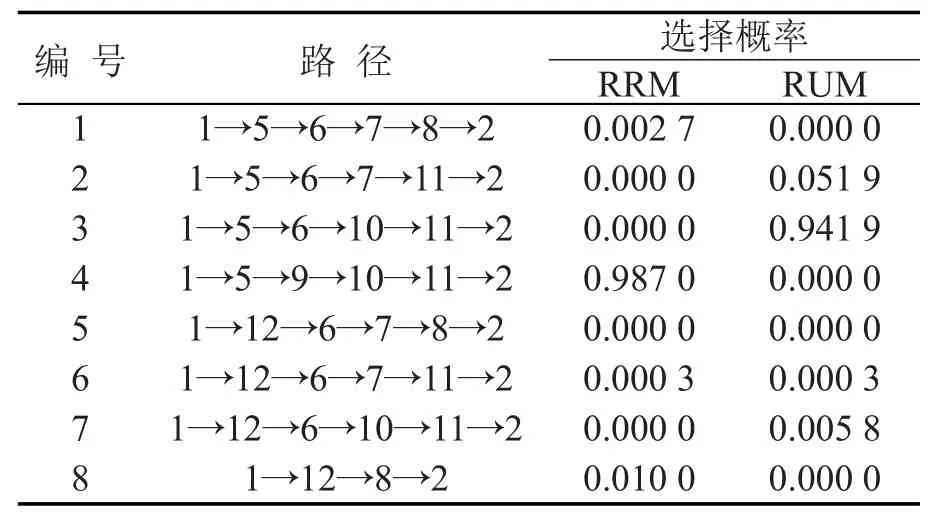
表1 起点1至终点2不同路径选择概率表Table 1 Routes and choice probability

从图4中可以得出，当重叠路径的长度x在0至100间移动时，采用传统的RRM模型，选择独立路径3的概率一直不变，为0.33.而采用基于效用改进参数的RRM模型，选择路径3的概率从0.33（当x=0时）增长至0.5（当x=100）时，即重叠路径的长度越长，选择独立路径的概率越大，更符合实际情况.

应用基于位置的RRM模型，分别计算图2所示的交通网络中时间剩余较长路径的选择概率如下：

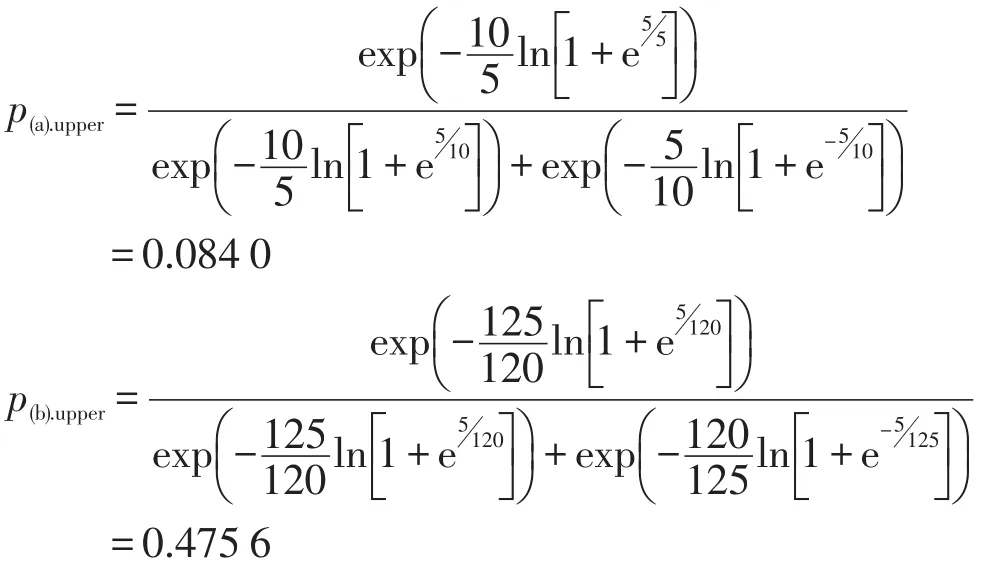
从结果可以明显看出，对传统的RRM模型进行改进后，图2（a）长路径的选择概率变化不大，而图2（b）长路径的选择概率有明显变化，更符合实际情况，证明了模型的合理性.

最后，通过示例性路网来验证本文提出的改进的基于时间剩余的随机后悔最小化模型，并跟RUM模型进行对比.

图5 示例交通路网图Fig.5 A sample network

如图5所示的路网，分别对节点和路段进行标号，其中加粗的路段位于CBD地区，实施拥堵收费政策，对于每一条路段实施在高峰期间固定收费，每一条路段的收费均为5.设无差异曲线方程为本文假设所有路径的旅行时间服从N( ) 2,0.28对数正态分布，进行一次模拟，分别计算基于时间剩余的RRM模型的选择概率和基于时间剩余的RUM模型的选择概率，其中RUM模型的研究已经非常成熟，本文不再赘述，可以参考McFadden[16]，由此得到由起点1至终点2的路径选择概率如表1所示.

5 研究结论

本文简要地回顾了路径选择中常用的随机效用最大化模型（RUM）和随机后悔最小化模型（RRM），并应用了西方经济学中无差异曲线的概念，考虑出行时间和出行费用的双重约束，建立了基于时间剩余的随机后悔最小化模型.由于RRM模型存在路径重叠及路径感知方差问题，本文将模型进行了改进，并且验证了改进模型的准确性.最后，本文应用所提出的模型计算了一个示例性交通路网中特定OD对间路径的选择概率，并与基于时间剩余的RUM模型进行了对比.

本文重点研究了路径选择理论，采用较小的路网进行测试，在未来的研究中，将本文的模型结合变分不等式理论，进一步构建为交通分配模型，并在较大规模的路网中进行测试.其次，RUM模型和RRM模型从本质上属于两种不同的行为经济学模型，如何将两种理论进行结合，分析出行者的路径选择模型，是未来研究的方向之一.

[1] Quattrone A,Vitetta A.Random and fuzzy utility models for road route choice[J].Transportation Research Part E: Logistics and Transportation Review,2011,47(6):1126-1139.

[2] Manski C.The structure of random utility models[J]. Theory and Decision,1977,8(3):229-254.

[3] Cascetta E,Papola.A random utility models with implicit availability∕perception of choice alternatives for the simulation oftraveldemand[J].Transportation Research Part C:Emerging Technologies,2001,9(4): 249-263.

[4] Danganzo C,Sheffi Y.On stochastic models of traffic assignment[J].Transportation Science,1977,11:253-274.

[5] Sheffi Y.Urban transportation networks:equilibrium analysis with mathematical programming methods[C]. Englewood Cliffs,N.J:Prentice-HallIncorporated, 1984.

[6] 鲜于建川,隽志才,朱泰英.后悔理论视角下的出行选择行为[J].交通运输工程学报.2012,3(12):67-72. [XIANYU J C,JUAN Z C,ZHU T Y.Travel choice behavior based on regret theory view[J].Journal of Traffic and Transportation Engineering,2012,3(12):67-72.]

[7] Chorus C.A generalized random regret minimization model[J]. Transportation Research part B: Methodological,2014,68:224-238.

[8] 栾琨,隽志才,倪安宁.出行路径选择的随机后悔最小化模型[J].交通信息与安全，2012,30(6):77-80. [LUAN K,JUAN Z C,NI A N.Random regret minimization model of travel route choice[J].Computer and Communication,2012,30(6):77-80.]

[9] Chorus C,Arentze T,Timmermans H.A random regretminimization model of travel choice[J].Transportation Research part B:methodological,2008,42(1):1-18.

[10] Chorus C.A new model of random regret minimization [C].EJTIR,2010.

[11] Chorus C,DeJong G C.Modeling experienced accessibility for utility-maximizer and regret-minimizers [J].Journal of Transport Geography,2011,19(6):1155-1162.

[12] Prato C G.Estimating random regret minimization models in the route choice context[C].Proceedings 13th International Conference on Travel BehaviourResearch, 2012.

[13] Wang J,Ehrgott M.Modelling route choice behaviour in a tolled road network with a time surplus maximization bi-objective user equilibrium model[J].Transportation Research Part B,Methodological,2013,57:342-360.

[14] Ji X F,Zhang J,Hu Y K,et al.Location-based route choice model under random regret minimization[C].14th COTA International Conference of Transportation Professionals,2014.

[15] Kitthamkesom S，Chen A.Modeling overlapping and heterogeneous perception variance in stochastic user equilibrium problem with weibit route choice model[J]. Transportation Research Part B:Methodological,2013, 57:378-397.

[16] McFadden D.Spatial interactiontheory and planning models[M].Amsterdam:North Holland,1978.

Route Choice Behaviour Based on Time Surplus Random Regret-minimization Model

LI Meng-tian1,2,JI Xiang-feng1,2,ZHANG Jian1,2,RAN Bin1,2
(1.Jiangsu Key Laboratory of Urban ITS,Southeast University,Nanjing 210096,China;2.Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies,Nanjing 210096,China)

The last step of conventional four-stage transport planning model,traffic assignment,is mainly based on the results of modeling the route choice behaviour of travellers.In order to overcome the drawbacks for the majority of travel choice model,random utility-maximization model,Chorus presented an alternative named random regret-minimization model.This paper proposes a dual-constrained random regret model rooted in the economic theory of indifference curve.Considering the case of overlapping and route perception variance,an improved formulation is provided,and the proposed model is tested in sample networks.Numerical results demonstrate the validity of the formulations.

traffic engineering;route choice;dual-constrained random regret-minimization model;time surplus;indifference curve;overlapping;route perception variance

2014-06-25

2014-09-21录用日期：2014-10-08

国家重点基础研究发展计划（2012CB725405）；国家自然科学基金（51308115）；东南大学优博基金（YBJJ1344）.

李梦甜（1990-），女，江苏南京人，硕士生.*通讯作者：bran@seu.edu.cn

1009-6744（2014）06-0158-06

U491

A