Stackelberg博弈下海盗活动地区海军护航选择优化

朱乐群，吕 靖，李 晶

（大连海事大学 交通运输管理学院，辽宁 大连 116026）

Stackelberg博弈下海盗活动地区海军护航选择优化

朱乐群，吕 靖*，李 晶

（大连海事大学 交通运输管理学院，辽宁 大连 116026）

为了优化海军在海盗活动区域的护航选择决策，更好地保护过往船舶，维护海上运输安全，在对实际护航行动涉及的海军与海盗两方主体博弈关系分析的基础上，建立了一个包括海军和海盗双方在内的非合作非零和Stackelberg博弈对双方行为进行描述，并选取双层规划模型将博弈关系进行数学转换.针对该双层规划模型的特点，采用基于灵敏度分析的启发式算法（SAB）对反应函数具体形式进行计算，并进行模型求解算法设计.最后，以索马里海盗活动区域为例进行实例分析，得出海军继续选择亚丁湾进行护航，海盗活动区域将向红海转移的结果，结果也说明了模型与算法的合理性.

水路运输；海军护航优化；Stackelberg博弈；海上通道安全；双层规划

1 引 言

近年来，海盗袭击、劫持船舶事件不断发生，严重威胁全球海上贸易与海上运输安全.目前，海军护航是保障海盗活动区域海上运输安全的主要手段.然而，由于海军护航舰艇数量有限，难以实现对所有海盗活动区域的护航覆盖；另一方面，随着海军护航行动的展开，海盗开始不断调整袭击区域以躲避海军对其打击.因此，海军必须在有限护航能力的前提下，根据海盗活动的新特点来对护航区域进行调整，以达到护航效益的最大化.因此，希望通过对该问题的研究为海军调整护航区域提供决策依据，以更好地保护过往船舶，维护海上运输安全.

现有关于海盗问题的研究大多集中在海盗行为经济性的考量，Anja Shortland[1]通过对大量文献的分析与实际数据的处理，对2008-2010年在亚丁湾执行任务的国际海军的效率进行了评价；Brishti Guha[2]研究了海盗对海上贸易的影响，计算了海盗活动产生的经济影响.除此之外，已有的危险货物运输网络规划研究对该问题有重要的借鉴意义，陈钢铁[3]进行了非合作下危险物品运输网络的双层模型及博弈研究，在政府和运输商的双层约束条件下设计了一个双层规划模型对危险物品运输网络进行优化；Allison Reilly[4]等建立了非合作非零和博弈模型对恐怖分子威胁下，政府关闭危险货物运输线路中重要基础设施的决策进行优化.本文在前人研究的基础上，分析海军与海盗的博弈关系，建立海军护航区域选择模型，通过求解模型的最优解来优化海军护航区域.

2 问题描述与模型建立

2.1 海盗活动区域海军护航选择问题

根据现有的海盗袭击案例，在该问题中，存在海军与海盗两个决策主体，海军的策略集为是否对各个区域实施护航，海盗的策略集为是否对各个区域实施攻击.海军的“支付”是护航带来的该区域的海上安全，海盗的“支付”是袭击为其带来的经济上的收益.海军与海盗之间存在下列一个动态的决策过程（图1）.

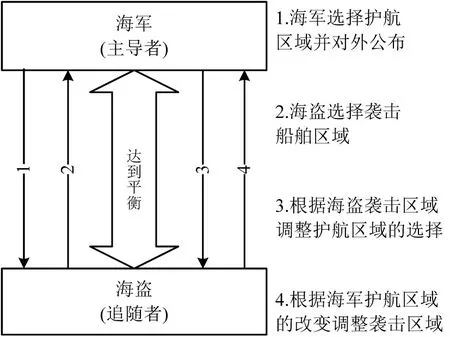
图1 海军与海盗的博弈过程Fig.1 The gaming process of navy and piracy

该问题构成了一个典型的Stackelberg博弈问题[5]，其中领导者为海军，海盗为追随者，可以用一个海军—海盗双层数学规划模型[6]来描述.

其中y(x)由下层规划问题求得，

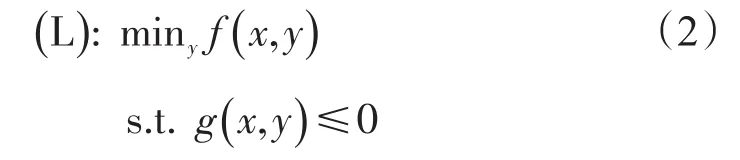
式中 F(x ,y(x) )——x是海军的决策目标函数和决策变量；

G——海军的决策变量相应的约束函数；

f和y——海盗的目标函数和决策变量；

g——海盗的决策变量相应的约束函数.

上层海军护航选择问题(U)的求解依赖于下层问题(L)，需要分别对两方行为进行建模.

2.2 海盗攻击区域分配模型

在海盗攻击区域分配模型中，海盗面临的决策是如何选择区域袭击，以达到收益最大化.假定海盗是利益追求者，利益最大化是其区域选择的主要因素，风险作为第二考虑.海盗的收益来自成功劫持船舶与船员，海盗面临的风险来自于船舶对海盗袭击的抵抗和附近护航军舰对船舶进行救援时对其的打击.以海盗行动收益为目标函数，以收益最大化为目标，建立海盗攻击区域分配模型.

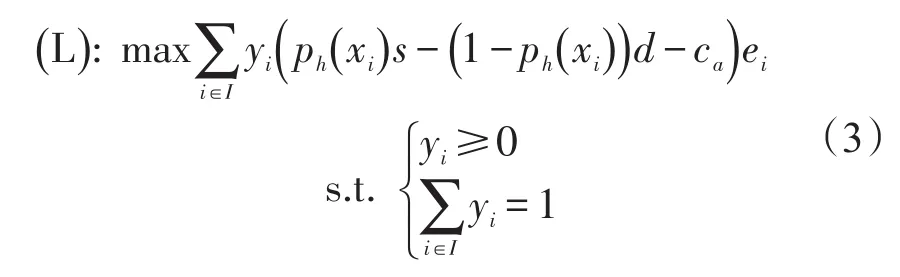
式中 I——所有海盗活动区域的集合；

i——代表一个海盗活动区域，i∈I；

xi——代表海军是否选择i区域进行护航，护航则为1，不护航则为0；

yi——代表海盗袭击每个区域的概率；

ph——代表海盗袭击每个区域时成功劫持船舶的概率，ph是x的函数；

s——代表海盗成功劫持船舶的收入；

d——代表海盗行动失败的损失；

ca——代表海盗每次袭击的成本；

ei——代表海盗袭击的区域修正系数.

由于各个不同区域的海况、距离海盗路上基地的距离不同，因此海盗对于不同区域存在不同的袭击倾向，据此设置了海盗袭击区域修正系数ei对各个区域的海盗袭击收益进行修正.

2.3 海军护航区域选择模型

海军护航行为的目的在于维护海上安全，保障过往船舶不受海盗袭击，因此以船舶通过海盗活动区域时受海盗袭击期望损失最小为目标.

式中 lh——代表遭受海盗劫持时船东的损失；

cd——代表船舶防御海盗袭击所产生的成本；

X——代表海军护航能力能够覆盖的区域数量；

fi——海军护航区域选择的修正系数.

由于各个区域海上船舶交通量不同，通行船舶的类型不同，对世界贸易的重要程度不同，因此通过设置区域修正系数 fi来对不同区域的期望损失进行调整.

2.4 海盗活动区域海军护航选择双层规划模型

因此海盗活动地区海军护航区域选择问题的双层规划模型描述如下：

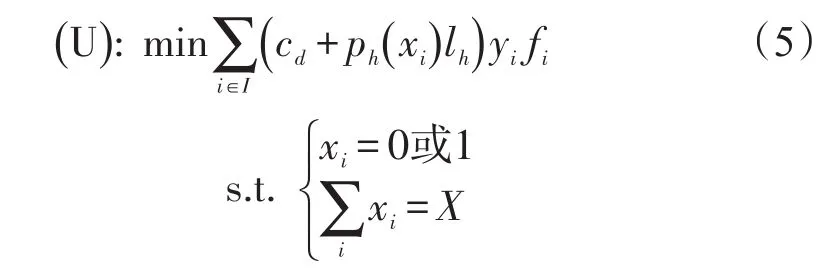
其中y由下层模型求得：

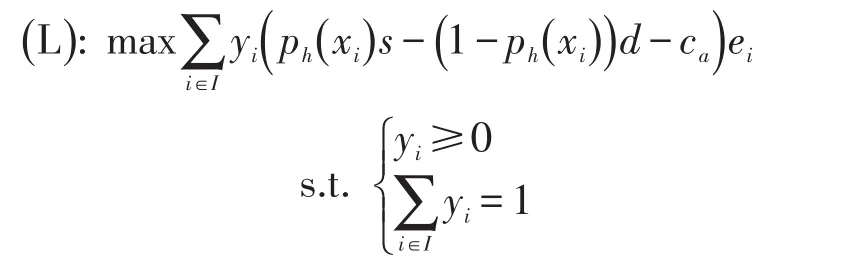
3 基于灵敏度分析（SAB）的启发式算法

双层规划是一个NP-hard问题，不存在多项式求解算法[5].但是如果可以找到反映领导层与从属层目标函数之间的具体反应函数y() x的形式，则可以转换为单层规划进行求解.对反应函数具体形式的求解，可以通过数学变换将一个有约束的最优化问题转化为等价的变分不等式，采用灵敏度分析求出变分不等式扰动参数的导数，继而得出变量间的导数关系，最后再运用泰勒展开式对反应函数求近似解，即采用基于灵敏度分析的启发式算法（SAB）[7].

在模型中，扰动参数为海军选择的护航区域 x.当下层模型 f(y)中存在海军护航区域选择的扰动参数x，即 f(y,x)变分不等式形式如式（6）所示.

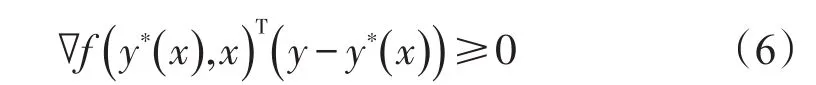
其中 y∈{y (x) |Y=y(x)∧T,y(x)≥0} ，y∗(x)为模型均衡解

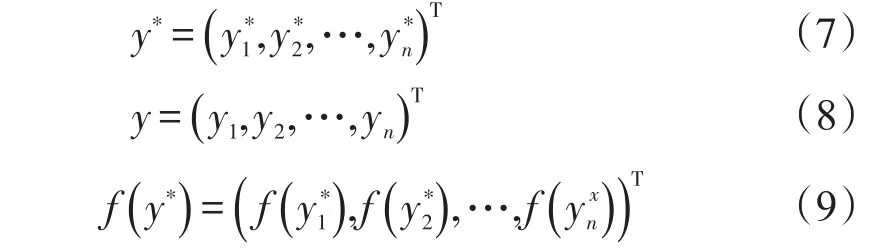
式中 ∧=(1 ,1,…,1)T∈En——维数是N、元素全是1的列向量.

假定已知变分不等式在x=x(0)时的解有且仅有y∗(x(0))，则在x=x(0)时解的必要条件为：

式中 μ——方程等式约束的拉格朗日乘子向量.

设Z(x)=[y (x),μ(x)]T，用 Jz(x)表示式（9）、式（10）对于 [y ,μ] 的雅克比矩阵，用Jx(x)表示式（9）、式（10）对于X的雅克比矩阵，则有

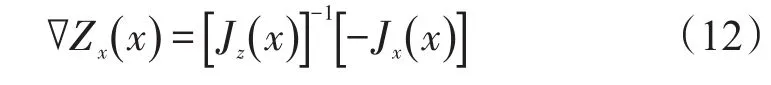
假定X(0)为海军护航区域选择的初始值，那么在这个初始值下可以通过求解从属层问题得到海盗的区域选择结果Y*(X(0)).并且通过灵敏度分析方法得出海盗攻击区域分配对海军护航选择的导数关系为，则反应函数的泰勒展开式近似为

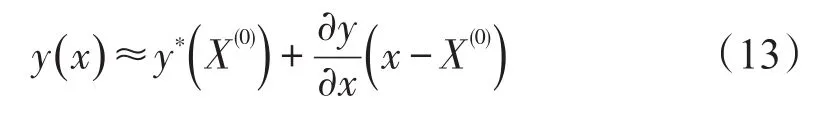
式（13）即为反应函数 y() x的具体形式，将其代入到决策层目标函数中，那么决策层问题就转化为一个普通的非线性优化问题，可以用已经存在的方法求解.而对于通过决策层问题来求的海军最优的护航区域，需要再次求解从属层问题，才能得到海军护航区域变化后的海盗袭击区域选择结果.根据上述思路，本文设计用于求解海军护航区域选择双层规划模型算法的具体步骤如图2所示.

图2 算法流程Fig.2 The step of algorithm

4 索马里海盗活动区域实例计算

4.1 索马里海盗活动区域划分

为了验证模型与算法的合理性，选取索马里海盗活动区域进行实证研究.通过对国际海事组织（IMO）公布的2010-2011年索马里海盗袭击船舶数据的处理，得到2010-2011年索马里海盗发动袭击船舶的地点分布如图3所示.因此共选择了五个护航区域（I），分别为亚丁湾（I1）、红海（I2）、阿拉伯海（I3），印度洋（I4）和索马里区域（I5）.

图3 2010-2011年索马里海盗袭击船舶地点Fig.3 2010-2011 Somalia piracy attack area’s location distribution

4.2 海盗攻击区域分配模型参数

海盗每次袭击的平均成本主要包括海盗行动所需的人力与物力成本，由于缺乏海盗袭击的详细资料，难以准确核算，但根据已有的研究，海盗每次行动的平均袭击成本ca为4万美元.

海盗的收益存在两种可能，一是船东拒绝支付赎金，海盗占有船舶，二是船东支付海盗要求的赎金.第一种情况下，船东拒绝支付赎金的情况多发生在海盗劫持渔船中，这时认为海盗的收益为110万美元.如果船东选择支付赎金，则根据近期船东支付赎金平均情况（表1），假定海盗的赎金收益为332万美元.根据以往海盗劫持船舶的案例，虽然政府呼吁拒绝向海盗支付赎金，但大部分船东（约90%）出于商业利益的考虑选择支付赎金，因此假定海盗劫持船舶成功的收益s为310万美元（332×0.9+110×0.1）.

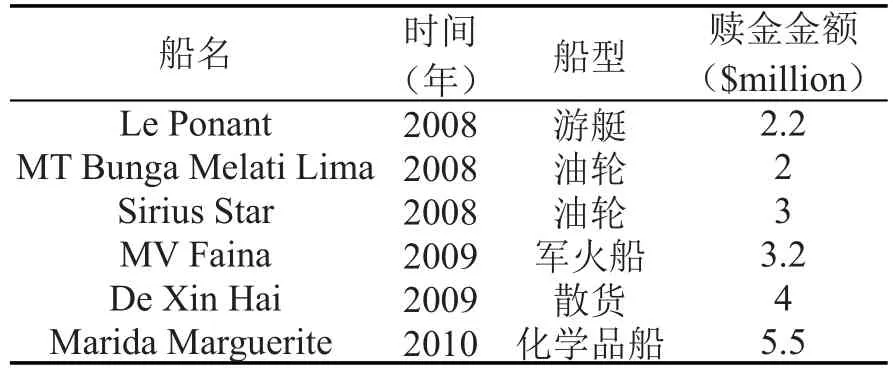
表1 索马里海盗劫持船舶赎金情况Table 1 The ransom of hijacked vessels by Somali piracy

如果海盗袭击失败，则意味着海盗在试图劫持船舶过程中遭遇了来自船舶的抵抗和附近海军护航力量的打击，在海盗劫持成本之外，海盗需承担由于人员伤亡带来的损失.根据Juan Carlos Sevillano[8]的相关研究结论，每名海盗的统计生命价值为25万美元.假定海盗袭击失败将导致2名海盗死亡，则海盗袭击失败的损失d为50万美元.

海盗成功劫持船舶率ph为x的函数，本文假定ph(x)采用幂函数形式，即ph(x)=axb+c，由于国际海军在亚丁湾护航开始于2008年末，本文通过对比分析2008年前后亚丁湾地区海盗劫持船舶成功率来确定常数a、b、c的值.如表2所示，根据2008年与2009年数据对常数a、b、c的值进行估计，c为0.35，a为-0.18，b为0.5，得出ph(x)=0.35-0.18x0.5

表2 2008-2011年索马里海盗劫持船舶成功率Table 2 The successful percent of hijacked by Somali piracy in 2008-2011

索马里海盗对各个区域存在不同的袭击倾向，自2008年起，由于海军在亚丁湾进行护航，使得海盗对袭击区域的选择发生改变，因此可通过分析2008年之前数据，得出海盗袭击倾向来对修正系数ei进行估计，为了使得系数更具可比性，对系数进行归一化处理，得到系数值为

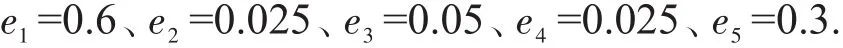
4.3 海军护航区域选择模型参数

船舶在通过海盗区域均会采取一定的防海盗措施会产生一系列的反海盗成本，根据Carney研究的结果，抵抗海盗袭击的平均成本cd为22万美元.

若船舶被海盗劫持，则遭受海盗劫持时船东的损失lh包括船东需要支付的船舶赎金及海盗在袭击过程中对船东造成的损失，平均赎金支付为332万美元.对船东造成的损失，主要是船体受损、船员伤亡及货物损失，由于船员伤亡的损失最大且容易衡量，因此只考虑船员伤亡带来的损失，假设在袭击过程中造成1名船员的死亡，Carlos Sevillano[8]测算一名西班牙船员的价值为265万美元，则lh为597万美元.

根据前文对海军护航现状的描述，目前由于海军护航能力有限，因此假定海军能够实施护航的区域数量X为1，随着海军护航力量的加大，X的取值可随实际情况进行变化.

海军护航区域修正系数 fi则通过各个区域通过的货运量与在全球航线中发挥的作用进行估计.该区域船舶实时AIS图如图4所示.根据现有航线情况和实时船舶AIS图的点分布情况对海军护航区域修正系数进行估计，同样进行归一化处理，得到如下结果：f1=0.35、f2=0.3、f3=0.2、f4=0.1、f5=0.05.

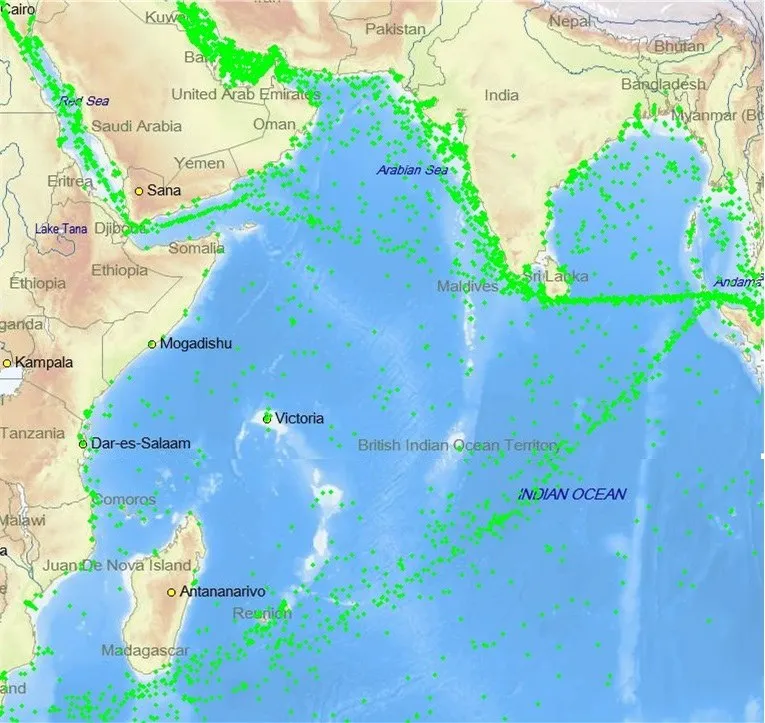
图4 索马里海盗活动区域船舶AIS图Fig.4 The AIS map of ships in the areas of Somali piracy

4.4 计算结果

按照已设计的算法进行编程，并将已计算的参数结果代入运算.初始化xi=[0，0，0，0，0]进行运算，经过5次迭代，运算结果收敛，得到海军护航区域选择结果xi=[1，0，0，0，0]，即海军选择集中力量在亚丁湾区域进行护航，得到相应最终海盗袭击分配结果，y1=0.185，y2=0.283，y3=0.050，y4=0，y5=0.482.又选取xi=[1，0，0，0，0]、xi=[0，1，0，0，0]、xi=[0，0，1，0，0]、xi=[0，0，0，1，0]和xi= [0，0，0，0，1]作为初始数据进行计算，5组初始数据收敛结果相同.

计算结果表明，虽然数据显示目前索马里海盗的袭击区域受海军亚丁湾护航的影响已经发生变化，但由于目前海军护航能力受限，海军目前最优的护航选择依然是继续实施亚丁湾护航.在海军继续维持亚丁湾护航的情况下，相应的海盗袭击概率的区域分配为亚丁湾区域0.185、红海区域0.283、阿拉伯海区域0.050，印度洋区域0和索马里区域0.482，海盗更加倾向于选择索马里区域和红海区域发动袭击，但由于索马里区域在所选区域中通过的货运量与在全球航线中发挥的作用较小，因此海盗活动的总体影响下降.

5 研究结论

本文研究了海盗活动区域的海军护航决策选择问题，在Stacklberg博弈基础上，设计了海盗活动区域海军护航选择模型对该问题进行描述，并根据索马里海盗活动的实际情况运用基于灵敏度分析的启发式算法进行了案例计算.本文的研究结果表明，模型可以预测海盗对护航区域设定的反应，海军在亚丁湾护航行动开始后，海盗将更倾向于选择索马里区域和红海区域实施袭击，在现有护航力量情况下，海军应对海盗袭击最优的护航区域选择依然为亚丁湾.结果较为符合当前海军的护航做法，说明本文模型与算法是合理可靠的，能够为海军护航区域选择决策提供支持.

[1] Anja Shortland，Marc Vothknecht.Combating“maritime terrorism”off the coast of Somalia[J].European Journal of Political Economy，2011，27:133-151.

[2] Brishti Guha,Ashok S Guha.Pirates and traders:Some economics of pirate-infested seas[J]. Economics Letters,2011，111:147-150.

[3] 陈钢铁,帅斌.非合作下危险物品运输网络的双层模型及博弈研究[J].兰州交通大学学报,2011,30(3):71-74.[CHEN G T，SHUAI B.Bi-level network model and game of non-cooperation dangerous goods transport[J]. Journal of Lanzhou Jiaotong University,2011,30(3):71-74.]

[4] Allison Reilly,Linda Nozick,Ningxiong Xu，et al.Game theory-based identification of facility use restrictions for the movement of hazardous materials under terrorist threat[J].Transportation Research Part E，2012，48:115-131.

[5] 黄松，杨超，杨珺.基于Stackelberg博弈的变质物品分销网络设计模型[J].中国管理科学，2009,17（6）：122-129.[HUANG S，YANG C，YANG J.Distribution network design model for deteriorating items based on stackelberg game[J].Chinese Journal of Management Science.2009,17（6）：122-129.]

[6] 李昌兵，杜茂康，付德强.求解双层规划问题的层次混沌量子遗传算法[J].系统工程学报,2013,28(2):159-166.[LI C B，DU M K，FU D Q.Hierarchical chaotic quantum-inspired genetic algorithm solving bi-level programming problem[J]. Journal of Systems Engineering,2013,28(2):159-166.]

[7] 曹守华，袁振洲，李艳红，等.交通流诱导条件下的路网随机平衡双层规划模型[J].交通运输系统工程与信息，2007,7(4):36-42.[CAO S H，YUAN Z Z，LI Y H，et al.A Model for road network stochastic user equilibrium based on bilevel programming under the action of traffic flow guidance system[J]，Journal of Transportation Systems Engineering and Information Technology，2007，7(4):36-42.]

[8] Juan Carlos Sevillano,David Rios Insua,Jesus Rios. Adversarial risk analysis the Somali pirates case[J]. Decision Analysis，2012，06:1-10.

Optimization of Zone Selection of Naval Escort in Pirates Active Areas Based on Stackelberg Games

ZHU Le-qun,LU Jing,LI Jing
(College of Transportation Management,Dalian Maritime University,Dalian 116026,Liaoning，China,)

To optimize the zone selection of naval escort for enhancing maritime security in pirates active areas.Firstly,the decision behaviors of the naval force and pirates in such areas are systematically analyzed. Secondly,a non-cooperative non-zero sum Stackelberg game is developed.The game builds the interactive relationships among the naval force and a pirate,which also can be described as a bi-level programming model.In order to solve this model,a heuristic algorithm called SAB is designed.Finally,the Somali pirates are taken as an example to implement the calculation.The results show that the best selection of naval escort zone is still the Gulf of Aden,while the pirates will be more willing to choose the Red sea area.The results also prove the rationality of models and the algorithm.

waterway transportation;optimized selection of naval escort;Stackelberg games;safety of sea line of communication;bi-level programming model

2014-06-18

2014-09-22录用日期：2014-10-08

教育部哲学社会科学研究重大课题攻关项目（11JZD049）.

朱乐群（1990-），男，江苏连云港人，博士生. *

lujing@dlmu.edu.cn

1009-6744（2014）06-0152-06

U698

A