基于统计提升准则的注塑工艺参数优化

谭 帅，彭 俊，李 闯

（1．东北大学 信息科学与工程学院，沈阳 110004；2．中能电力科技开发有限公司，北京 100034）

基于统计提升准则的注塑工艺参数优化

谭 帅1，彭 俊1，李 闯2

（1．东北大学 信息科学与工程学院，沈阳 110004；2．中能电力科技开发有限公司，北京 100034）

为了同时改善生产平板型注塑制品时的总体收缩度和收缩均匀度，提出基于统计提升准则的注塑成型工艺参数的多目标优化方法，寻找平衡两个质量指标的优化设计．首先利用小规模的实验设计方法获得建模数据集，针对应用中存在的建模数据奇异点问题提出一种数据预处理方法，并依此分别建立两个指标的初始替代模型，用于代替优化过程中代价高昂的计算分析；随后依据Pareto统计提升准则寻找新的采样点加入建模数据集来重新建模，使寻优结果不断趋近真实的Pareto前沿．仿真结果表明，较常规的建模优化方法，本文提出的方法能使用较少的采样数据，显著地改善平板制品的收缩质量．对于HDPE材质的矩形制品，保压曲线先恒定后线性递减可以获得好的收缩均匀度，使用压力上限值恒定保压可以获得好的平均收缩度．

注塑成型；收缩；多目标优化；统计提升准则；Kriging模型

制品收缩是注塑成型工艺中的重要质量指标．影响收缩指标的最关键工艺是保压阶段，保压压力的大小及其作用时间对制品的收缩有显著影响［1－2］．X．Chen、C．Li等［3－4］采用收缩匀度为指标，将保压曲线作为优化变量，未考虑其他工艺参数．K．M．B．Jansen等［5］通过实验分析得到，对于半结晶材料，各工艺参数中保压压力对收缩影响最大，模具温度次之；但论文只给出各参数对总体收缩影响程度的定性分析，并未在工艺参数可行范围内，给出最优的工艺设定解．

使收缩均值和均匀度都尽可能达到最优，是一个双目标优化问题．对于这类问题，往往无法找出能够同时使2个指标都达到最优的可行解，取而代之的是求出一组非支配解集（Pareto解集），解集内任一解均部分优于其他解，该解集对应的目标函数曲线被称为Pareto前沿［6］．获取Pareto解集最简单的方法是标量化方法，比如目标加权法［7］；另一种方法是一次性求取Pareto解集的多目标优化方法，NSGA－Ⅱ是此类方法的代表［8－9］．以上两类方法都建立在精确的优化模型基础上，可利用替代模型来拟合真实模型［10］．建立精确的替代模型需要大量建模数据，为进一步减少计算代价，J．Knowles等［11］提出了一种多目标迭代优化方法，但由于采用标量化方法来转化多目标问题，因此也继承了标量化方法的缺点．为克服这个缺点，A．J．Keane等［12］提出一类Pareto统计提升（SI）准则，折衷算法的全局和局部搜索能力，将局部搜索和全局收缩能力结合到一起，迭代结果可以覆盖整个Pareto前沿．

本文采用基于Kriging替代模型的迭代寻优方法，并引用Pareto SI准则，来解决双目标优化问题；同时，针对应用中存在的一类数据奇异点，分析了其对迭代寻优过程的恶劣影响，并提出了一种数据预处理方法，用于克服这种影响；最后，将带有数据预处理的迭代优化方法，用于基于制品收缩均值和均匀度指标的双目标优化问题，并从工艺角度对寻优结果进行分析解释．

1 替代模型

1．1 K riging模型

Kriging模型实际上是一种插值模型，该模型的优势在于它不仅能给出可行域任意点的预测值，还能够给出该预测值的不确定度．已知可行域内的N个k维样本点[x（1），x（2），…，x（N）]，其对应的输出响应y＝[y（1），y（2），…，y（N）]T，定义样本点x（i）与可行域内任一点x对应响应值的相关函数为

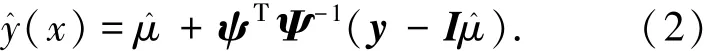
式中：θm和pm为第m维输入对应的待定模型参数；I为N维单位列向量；

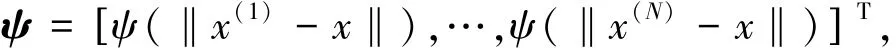
可逆矩阵Ψi，j＝ψ（‖x（i）－x（j）‖），i，j＝1，2，…，N，常数

如果将确定的函数y（x）视为满足高斯分布的随机过程Y（x）的一个实现，那么对于目前已知的输出响应y（满足高斯分布），Y（x）在任一点x处的均值和方差分别为式（2）和

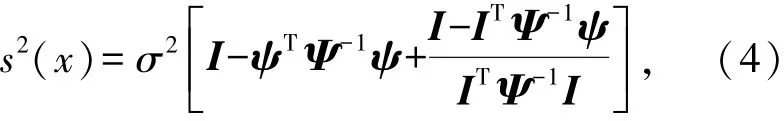
其中

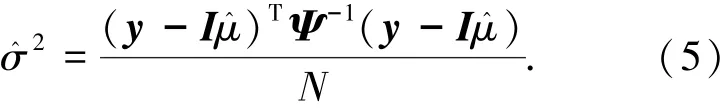
1．2 Pareto SI准则

设待插值的2个函数为f1e（x）和f2e（x），对应输出响应为y1和y2，由N个初始采样得到包含M0个采样的初始Pareto解集

其对应的Pareto前沿如图1所示．

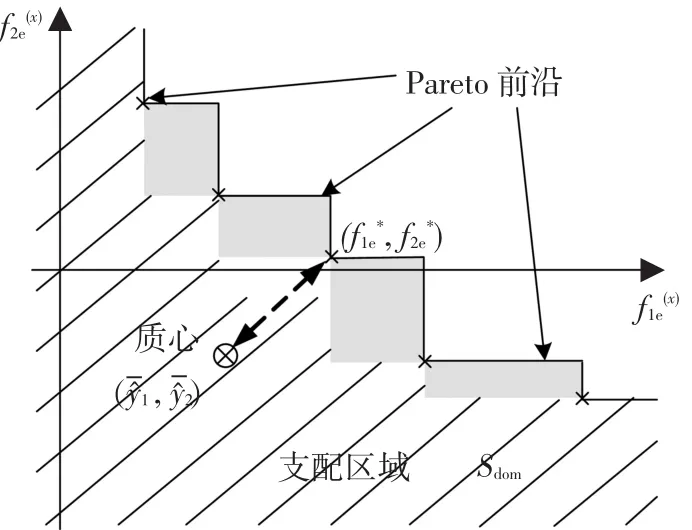
图1 Pareto前沿及其支配区域示意图

假设由N个训练数据对，分别插值得到的一对Kriging替代模型1（x）和2（x）彼此是独立的，可行域内任意点x对应预测值和及其标准差分别为μ1、μ2和s1、s2，那么1（x）和2（x）对应的二维联合概率密度函数为

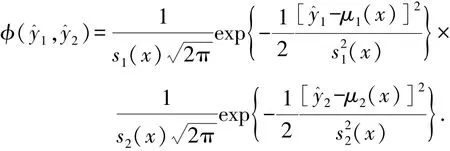
显然，当采样点响应值位于图1中Sdom区域时，初始Pareto前沿提升较大，因此这里要找到可行域内最有可能落入Sdom中的点作为新加入点，即最大化概率提升

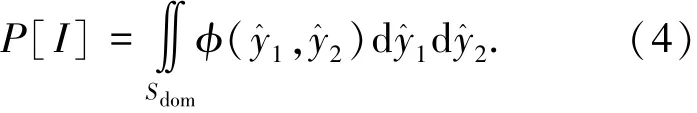
除了概率提升，还可以最大化期望提升．考虑指标提升的幅度

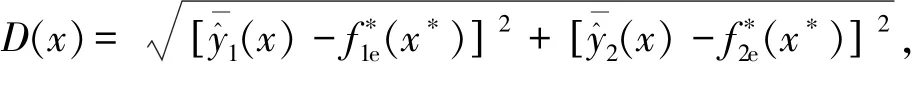
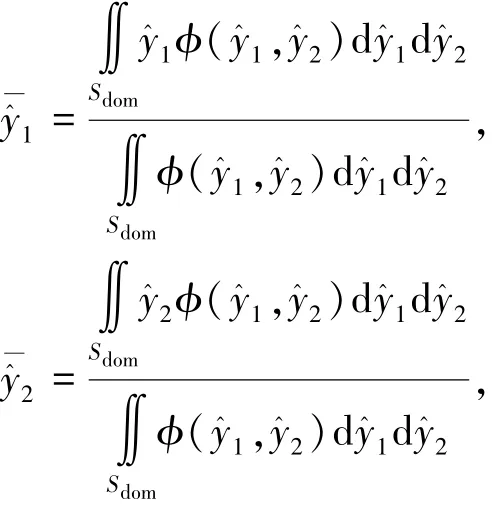
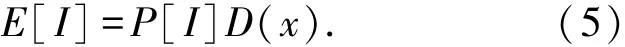
由于考虑了预测误差的不定度，2个统计提升函数E［I］和P［I］都具备全局搜索能力．但E［I］考虑了指标提升的幅度，因此实际优化时它的搜索幅度较P［I］更大，并且E［I］也与2个指标的加权系数有关，而P［I］则无关．

2 优化策略的实现

2．1 数据预处理

基于替代模型的多目标迭代优化过程可概括为，利用初始采样数据建模，再根据Pareto SI准则寻找新的加入点，加入训练数据集后重新建模，如此循环直至满足收敛准则，显然建模准确与否是迭代优化能否正确进行的基础．尽管Kriging方法适用于插值高度非线性模型，但前提是被插值模型是光滑和连续的［14］，然而在实际的寻优问题中，常会在可行域内出现一些数值相对较大或较小的奇异点，如图2（a）所示，这将直接影响建模结果，从而影响迭代寻优过程．

图2 带有奇异点的函数及其分段压缩过程

为了限制奇异点的幅值，同时又不改变响应值的相对大小，这里采用奇异点线性变换的方法来解决该问题．基本思想如图2（b）所示，首先根据初始采样数据的分布，设定监测来判断奇异点，一旦新采样超过监测限，则进行数据压缩，即把从压缩限到奇异点的响应值，线性变化到压缩限与监测限之间．这样做就把奇异点压缩到正常范围，从而保证建模和迭代寻优过程的进行．

2．2 迭代优化策略的流程

带有数据预处理步骤的多目标迭代优化方法的实现流程如图3所示，具体步骤如下：

图3 带预处理步骤的双目标迭代优化流程图

1）数据产生．使用拉丁超立方方法产生N个初始采样点，拉丁超立方是一种实验设计方法，具有抽样次数少结果稳定的特点［15］．再通过实验产生与输入对应的N对响应值．

2）首次数据预处理．分别根据两种指标的响应值，计算出指标对应的监测限和压缩限，并对超出压缩限数据进行压缩．令监测上下限为Ru和Rd，压缩上下限为Cu和Cd，具体定义如下：

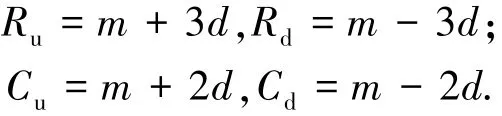
式中，m为N个响应的均值，d为标准差．如果最大值响应y（s）（奇异点）超出Ru，（s）为y（s）压缩后的数值，设y（i）为待压缩的采样值，y～（i）为y（i）压缩后的结果，那么

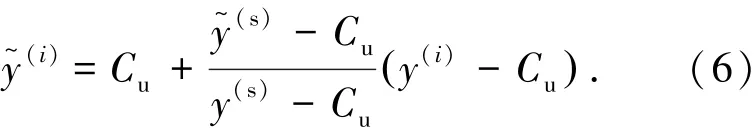
3）建立模型．分别利用采样数据对，建立2个指标的Kriging模型，即采用极大化似然函数的方法［14］，获得式（1）中的待定参数p和θ．

4）寻找加入点．在可行域内优化式（4）或式（5），找到当前插值模型下的一个全局提升加入点．

5）终止准则．如果加入点数达到初始采样个数N的一到两倍的时候，迭代寻优终止，否则进入步骤6．

6）获取新响应值后，再进行处理．对新加入采样要先获取其对应响应值，如果其超出当前压缩限，先对其进行压缩，若压缩后仍超出监测限（新的最大值出现），则用它替换掉式（6）中的y（s），再用式（6）对所有超出压缩限的采样重新压缩，之后回到步骤3，重新进行建模．

3 迭代优化实例

本例选取多目标函数［8］

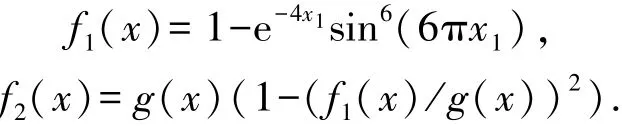
图5和图6分别给出了Kriging模型参数随迭代进行的变化情况，这里实线和虚线分别表示带有和不带有预处理步骤时的情况，而细线表示θ1参数，粗线表示θ2参数．从图6中可明显看出：当迭代进行到10次之后，不带预处理步骤时拟合出的模型参数迅速到达边界，这说明模型已经不能正确描述实际函数f2（x）了；而带有预处理步骤的参数则一直在正常的范围内波动．同时，在f2（x）的Kriging模型恶化之后，f1（x）的Kriging模型参数也开始加剧震荡，进而Pareto EI准则也随之失效，Pareto前沿很难再向理想前沿靠近了．

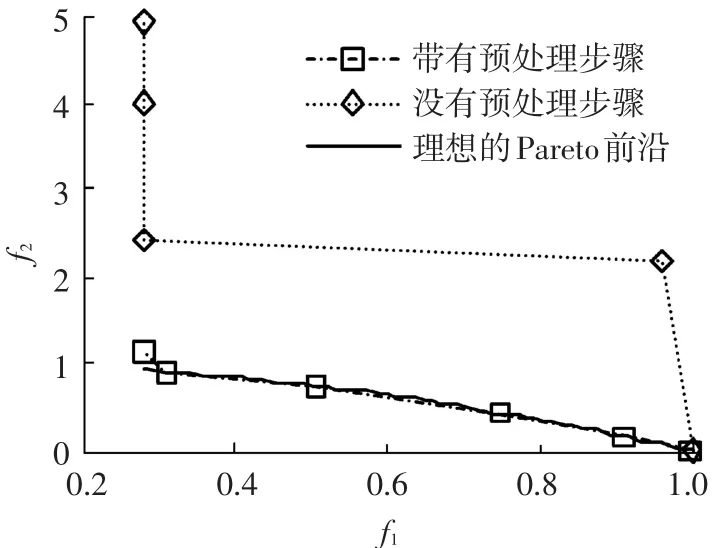
图4 带有和不带有预处理步骤优化所得的Pareto前沿

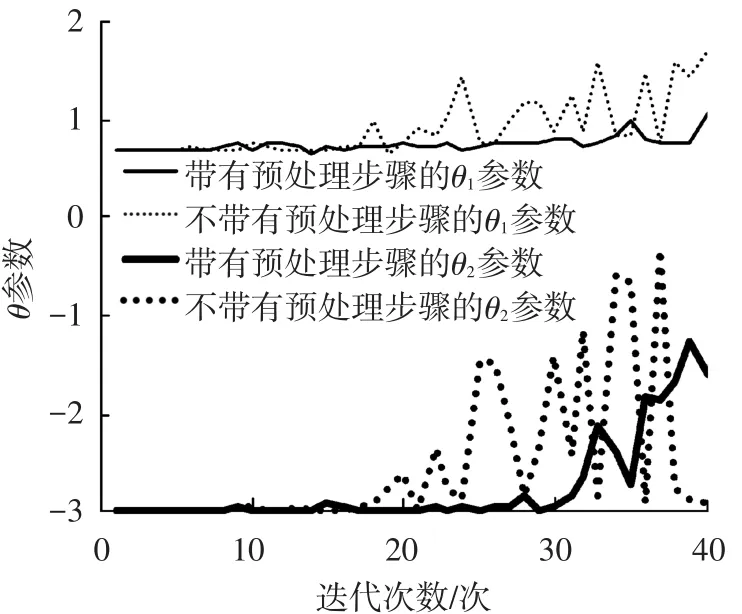
图5 函数f1（x）的K riging模型参数随迭代的变化情况

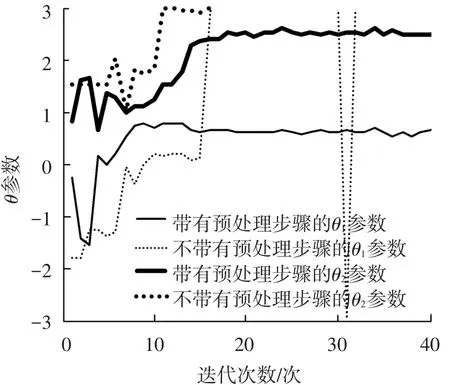
图6 函数f2（x）的K riging模型参数随迭代的变化情况

4 平板型制品质量的多目标优化

4．1 优化模型

本文用于研究保压曲线优化的注塑制品形状如图7所示，它是一个规格为150 mm×30 mm× 2 mm带有扇形浇口的矩形制品．材料选用Dow Chemical USA生产的牌号为Dowlex IP－10的HDPE．制品总体收缩指标采用制品顶出时各点体积收缩率的均值来表示，而均匀度指标则采用标准差表示．这里在图7中等间隔选取18个点，来计算收缩率的2个统计量：

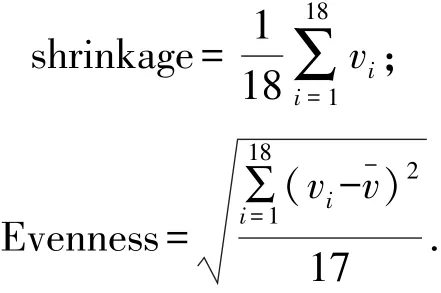
式中：vi表示图中第i个点的体积收缩；表示所有检测点收缩的均值，显然，该指标越小制品质量越均匀．

根据注塑工艺分析，保压曲线是影响2个收缩指标最关键的因素；而相对模具温度和熔体温度，注射速度对2个指标的影响最为间接．针对HDPE材质的矩形制品，Jansen等人［5］通过收缩指标影响因素分析实验，也给出了相似的结论．因此，这里确定优化变量为保压曲线、模具温度和熔体温度．

图7 矩形制件及其浇注系统的Fusion网络模型

保压曲线定义为先恒压后线性递减的形式．恒压压力设定为注塑机合模力可承受的上限［4］，这里选为100 MPa；最大保压时间应保证大于在最高的模具温度θmold和熔体温度θmelt下的浇口封死时间，这里选为10 s．这样，保压曲线就可以由保压曲线转折时间t，以及曲线的下降倾角ϕ两个参数来描述，如图8（a）所示．该描述可以表示恒定保压（ϕ＝0°或ϕ＝90°）和先恒定后递减保压（0°＜ϕ＜90°），此外还可表示保压时间小于10 s的情况，如图8（b）所示．

图8 保压曲线的两种形式

至此，优化问题可以描述为

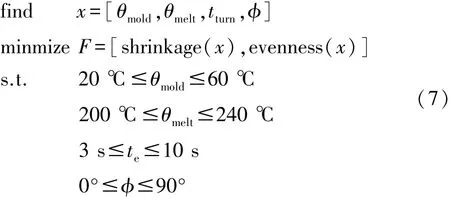
4．2 优化结果及分析

按照2．2节流程图，首先取40组初始输入采样，而后使用Moldflow对制品生产进行仿真分析获取收缩均值和均匀度，获得Pareto解集，如表1所示．仿真时，保压曲线形状参数以外其它的工艺参数设定如下：恒定注射速度40 mm/s．应用带有数据预处理方法的多目标迭代优化策略对过程进行优化，并将2个指标分别进行规一化处理，使Pareto EI准则不带有偏好，数据压缩边界仍取为y～（s）＝m＋2．9d．经过60次迭代，获得一个由实际采样组成的Pareto解集，如表2所示，其中最优收缩均值和均匀度，分别对应于1号和8号工艺设计．解集对应Pareto曲线如图9中的实线所示，与初始40个采样对应的Pareto曲线（如图9中虚线所示）比较，迭代使Pareto前沿有了显著的提升．

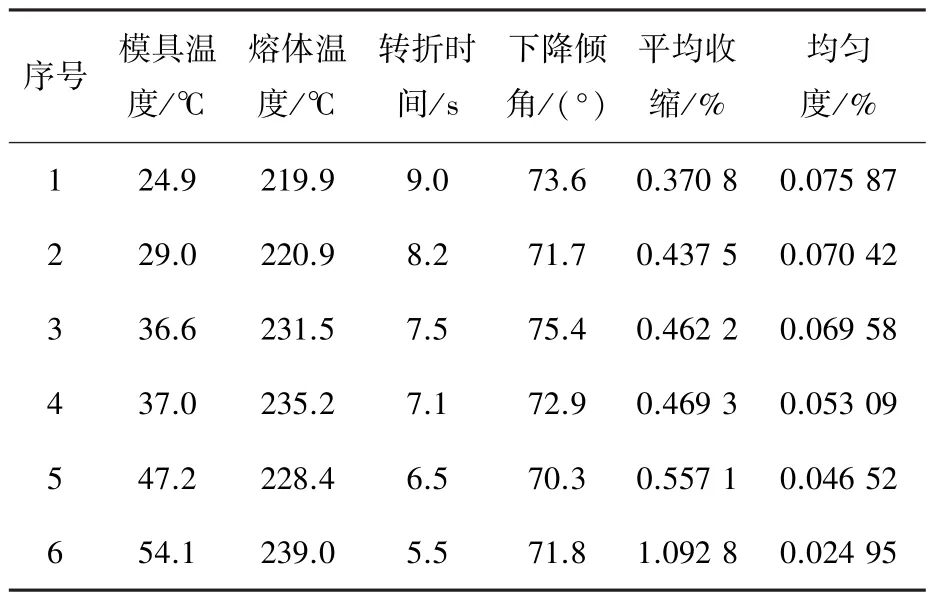
表1 初始采样对应的Pareto解集

表2 基于收缩指标的注射工艺参数双目标优化问题的Pareto解集

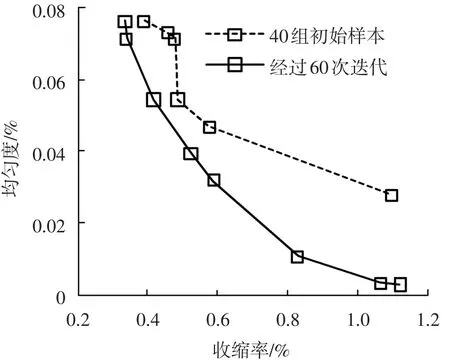
图9 初始采样和迭代优化后采样的Pareto前沿

由表2可知，最优收缩均匀度设计对应解集中最低的模具温度和较低的熔体温度，而最小平均收缩设计正与之相反．这是因为较高的模具温度使得制品的凝固时间增长，对于收缩均值，这将使得HDPE制品的结晶度较高，从而加大制品的总体平均收缩；而对于收缩均匀度，这将导致保压压力对制品作用时间长且传递较均匀：因此制品收缩分布会随温度升高而变得更加均匀．熔体温度对制品收缩的影响与模具温度相似，但是却没有模具温度作用显著．这从表2中2个收缩指标随着2个温度变化的趋势和程度上就可以看出．

最优收缩均值和均匀度设计对应的保压曲线分别如图10（a）和（b）所示．

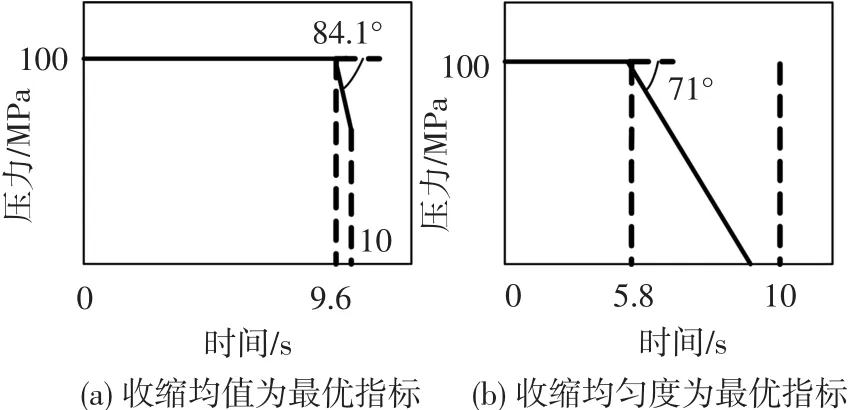
图10 最优指标对应的保压曲线

表面上看，两者都是先恒定后线性递减的保压曲线，但如果考虑制品浇口封死时间，那么两者的实际作用时间都会缩短．通过Moldflow仿真可知，对于图10（a）该时间为6．2 s，而对于图10（b）则为8．5 s．这样最优均值设计的保压曲线等价于恒定保压曲线，而最优均匀度设计的保压曲线仍是先恒定后递减型的，解集里其余的设计则是两者之间的过渡．前者容易理解，因为若想使制品总体收缩最小，必然要使用恒定的最大保压曲线来保压；后者则不然，远浇口（图7中制品B处）未冻结之前，即5．8 s之前应采取最大保压压力，以使制品各处收缩最均匀，但从此刻开始直到浇口封死，则应采用递减保压曲线，以使远近浇口的收缩差异减小，令制品更均匀［4］．

4．3 决策制定

获得Pareto解集后，必须从中选取一个解作为最终的优化结果，这个过程通常被称为决策制定．一种简单的决策方法是，分别计算Pareto解集内的解与理想点的距离，选择距离理想点距离最小的解作为最终决策解．对于本文的双目标优化问题理想点是［0．335 2，0．002 64］，为消除目标幅值对距离的影响，先对Pareto解集及理想点归一化之后，再进行数据点差异程度计算，结果如表3所示，显然应选择数值最小的设计4作为最终优化解．

表3 理想点与Pareto解集内阁点之间的差异程度

上述方法只考虑了Pareto解集内各点与理想点的距离，从注塑工艺角度看，这未必是最优的．实际生产中，除了希望优化两个收缩指标外，还希望注塑成型周期尽可能短，或者最优解的鲁棒性强等等．如果考虑成型周期就可以选择模具温度和熔体温度较低，所需保压和冷却时间短的设计；如果考虑最优解的鲁棒性，就要通过进一步的灵敏度实验来分析判别．具体用哪种策略，需要根据实际生产的需求来确定．

5 结 论

本文针对注塑制品收缩指标的双目标优化问题，采用基于Kriging替代模型的迭代寻优方法．该方法在迭代过程中使用现有采样数据及Pareto SI准则，来确定新的数据加入点，使得采样集的Pareto前沿不断趋于理想前沿．此外本文还提出了一种数据预处理方法，用于克服奇异点对该迭代寻优过程的坏影响．实际应用结果表明，迭代优化方法通过初始采样以外的60次实验，使得Pareto前沿显著提升．

通过对Pareto解集的工艺分析可知，对于HDPE材质的矩形制品，若想获得最优收缩均匀，模具温度越高越好，保压曲线应为先恒定后线性递减；若想获得最优的平均收缩，模具温度越低越好，保压曲线应使用压力上限值恒定保压．最终进行决策制定时，应考虑实际生产需求，从Pareto解集中选择最能满足实际需求的解作为最优设计．

［1］ROSATO D V，ROSATO M G．Injection MoldingHandbook［M］．3rd ed．Boston：Kluwer，2000．

［2］周云郊，兰凤崇，黄信宏，等．钢铝板材压力连接模具几何参数多目标优化［J］．材料科学与工艺，2011，19（6）：86－99．ZHOU Yunjiao，LAN Fengchong，HUANG Xinhong，et al．Multi⁃objective optimization of geometry of clinc⁃hing tools for steel⁃aluminum blank sheets［J］．Materi⁃als Science and Technology，2011，19（6）：86－93．

［3］CHEN Xi，GAO Furong．A study of packing profile on injection molded part quality［J］．Materials Science Engineering：A，2003，358（1/2）：205－213．

［4］LIChuang，WANG Fuli，CHANG Yuqing，et al．A modified global optimizationmethod based on surrogate model and its application in packing profile optimiza⁃tion of injectionmolding process［J］．Int JAdv Manuf Technol，2010，48（5）：505－511．

［5］JANSEN K M B，Van DIJK D J，HUSSELMAN M H．Effect of processing conditions on shrinkage in injec⁃tion molding［J］．Polymer Engineering Science，1998，38（5）：838－846．

［6］KNOWLES J，CORNE D，DEB K．Multiobjective Problem Solving from Nature：from Concepts to Appli⁃cations［M］．Berlin：Springer⁃Verlag，2007．

［7］KIM I Y，De WECK O L．Adaptive weighted sum method for multiobjective optimization：a new method for Pareto frontgeneration［J］．StructMultidisc Optim，2006，31（2）：105－116．

［8］DEB K，PRATAP A，AGARWAL S，etal．A fast and elitistmultiobjective genetic algorithm：NSGA⁃II［J］．IEEE Transactions on Evolutionary Computation， 2002，6（2）：182－197．

［9］金溪，高金良，张杰，等．利用NSGA－Ⅱ算法求解供水管网优化改造模型［J］．哈尔滨工业大学学报，2008，40（12）：1969－1976．JIN Xi，GAO Jinliang，ZHANG Jie，et al．Optimal re⁃habilitation model of water supply network with non⁃dominated genetic algorithm⁃II［J］．Journal of Harbin Institute of Technology，2008，40（12）：1969－1976．

［10］WILSON B，CAPPELLERI D，SIMPSON W，et al．Efficient pareto frontier exploration using surrogate ap⁃proximations［J］．Optimization Engineering，2001，2：31－50．

［11］KNOWLES J，HUGHESE J．Multiobjective optimiza⁃tion on a budget of 250 evaluations［J］．Evolutionary Multi⁃Criterion Optimization，LNCS，2005，3410：176－190．

［12］KEANE A J．Statistical improvement criteria for use in multiobjective design optimization［J］．AIAA Journal，2006，44（4）：879－891．

［13］RASMUSSEN C E，WILLIAMS C K I．Gaussian Processes for Machine Learning［M］．Massachusetts：The MIT Press，2006．

［14］FORRESTER A IJ，KEANE A J．Recent advances in surrogate⁃based optimization［J］．Progress in Aerospace Sciences，2009，45（1/2/3）：50－79．

［15］SACKS J，WELCH W J，MITCHELL T J，et al．Design and Analysis of Computer Experiments［M］．Berlin：Springer⁃Verlag，2003．

（编辑 程利冬）

M ulti⁃objective optim ization of injection molding process parameters based on statistical im provement criterion

TAN Shuai1，PENG Jun1，LIChuang2

（1．School of Information Science＆Engineering，Northeastern University，Shenyang 110004，China；2．ZhongNeng Power Technology Development Co．Ltd．，Beijing 100034，China）

To improve the shrinkage and evenness of the production of injection molded slab，this article introduces an iterativemulti⁃objective optimizationmethod based on Kriging surrogatemodel to find the Pareto set of the optimization problem．The idea of the iterative optimization method is first to establish two approximation function relationships between those index and process parameters by a small size of design of experiment（DOE）with surrogate model to alleviate the expensive computational expense in the optimization iterations．And then statistical improvement criterion of Pareto front is used to provide direction in which additional training samples could be added to better the surrogatemodel．This process will loop and bring the optimization result close to the ideal Pareto front．Simulation results show that amuch better shrinkage quality ofmolded part can be achieved with the proposed method with smaller amount of samples compared with traditionalmodeling and optimization method．For rectangular HDPE products，good evenness can be gotten using linear decreasing pressure curve after a period of constant value，and good shrinkage can be gotten using holding pressure with upper limits．

injection molding；shrinkage；multi⁃objective optimization；statistical improvement criterion；krigingmodel

TQ 320．66

A

1005－0299（2014）02－0068－07

2013－10－02．

中央高校基本科研专项资金资助项目（N120304004）；中国博士后科学基金资助项目（2013M530937）．

谭 帅（1983－），女，博士．

谭 帅，E⁃mail：tanshuai＠ise．neu．edu．cn．