两类与等差数列有关的组合恒等式
萧振纲
(湖南理工学院, 湖南 岳阳 414006)
两类与等差数列有关的组合恒等式
萧振纲
(湖南理工学院, 湖南 岳阳 414006)
巧妙地构造出一个多项式, 利用著名的Lagrange插值公式和L′Hospital法则, 得到了两类与等差数列有关的新颖而深刻的组合恒等式.
∶ Lagrange插值公式; 等差数列; 组合恒等式
先给出一条引理.
引理设f(x)是一个次数不超过n的多项式, 则
ⅰ) 对任意复数x, 恒有
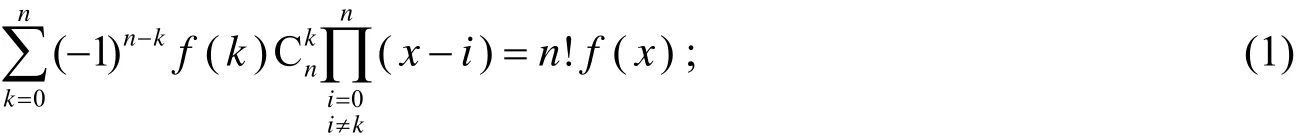
ⅱ) 当x≠0,1,…,n时, 有
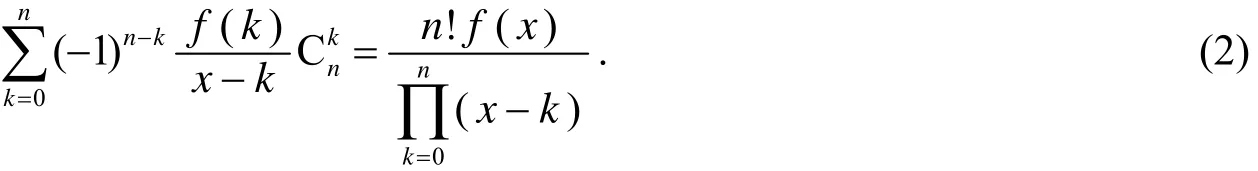
证明因f(x)是一个次数不超过n的多项式, 由Lagrange插值公式[1], 对任意n+1个互不相同的数x0,x1,…,xn, 恒有
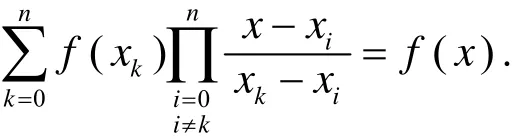
于此式中, 取xk=k,k= 0, 1, …,n, 并注意

定理设是公差分别为d1,d2, …,dn+1,d的等差数列, 且bk≠0(k= 1, 2, …,n),d≠0, 则有
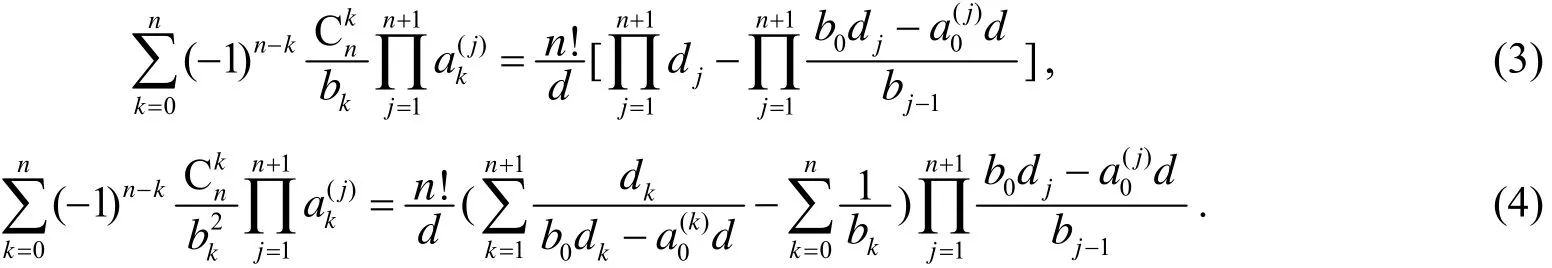
证明作多项式
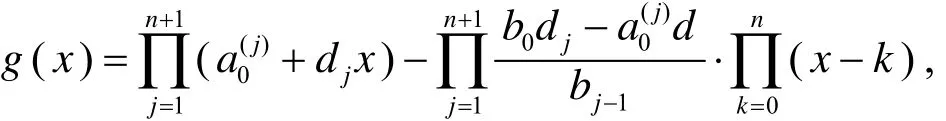
则g(x)的次数不超过n+1. 显然

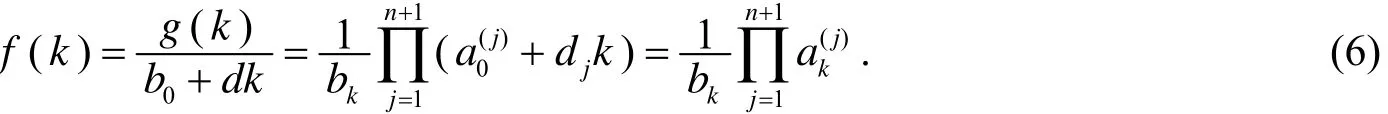
于是由(1)式, 有
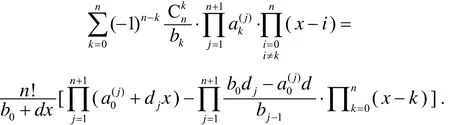
比较等式两边xn项的系数即得(3)式.
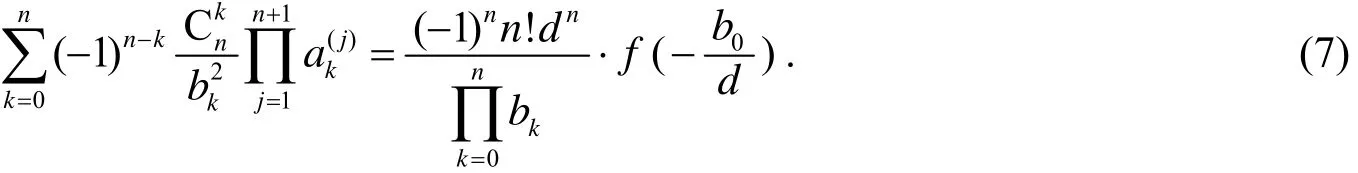
由L′ Hospital法则[2],有
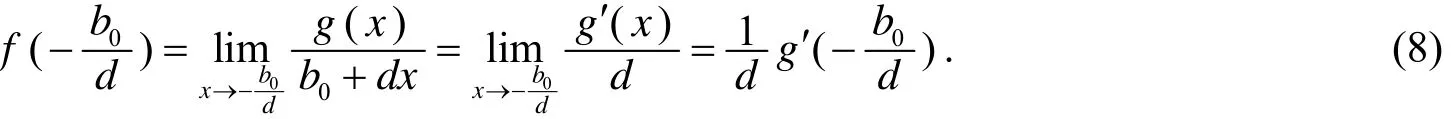
又不难知道

因而由(5)式容易得到
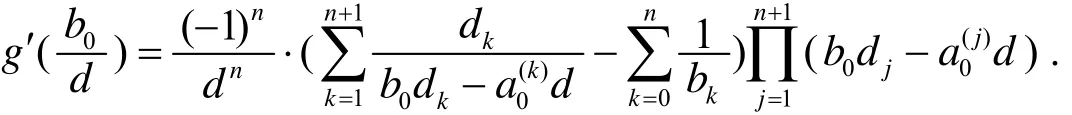
再由(7)、(8)两式立即得到(4)式.
推论1设是公差分别为d1,d2, …,dn+1的等差数列, 则有
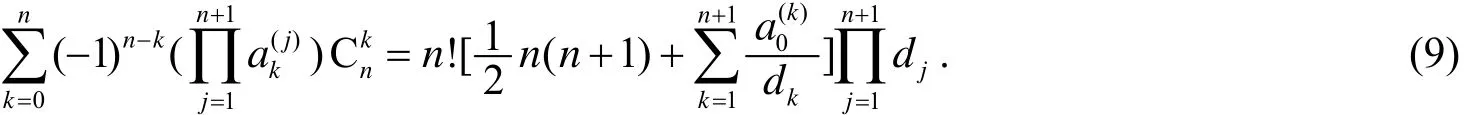
证明于(3)式中, 令b0=1, 则当d→0时, (3)式的左边→(9)式的左边. 又
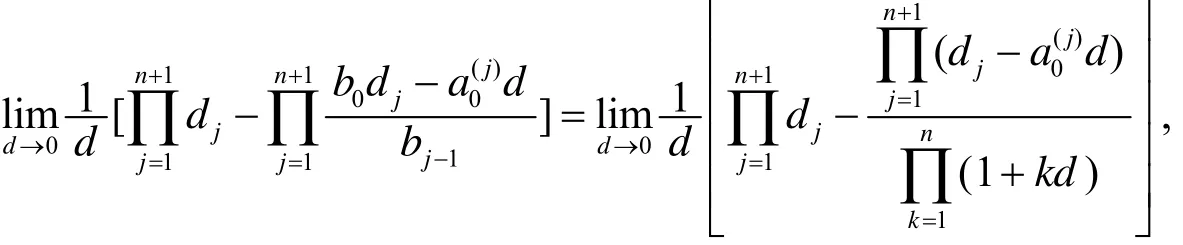
于是, 由L′ Hospital法则, 有
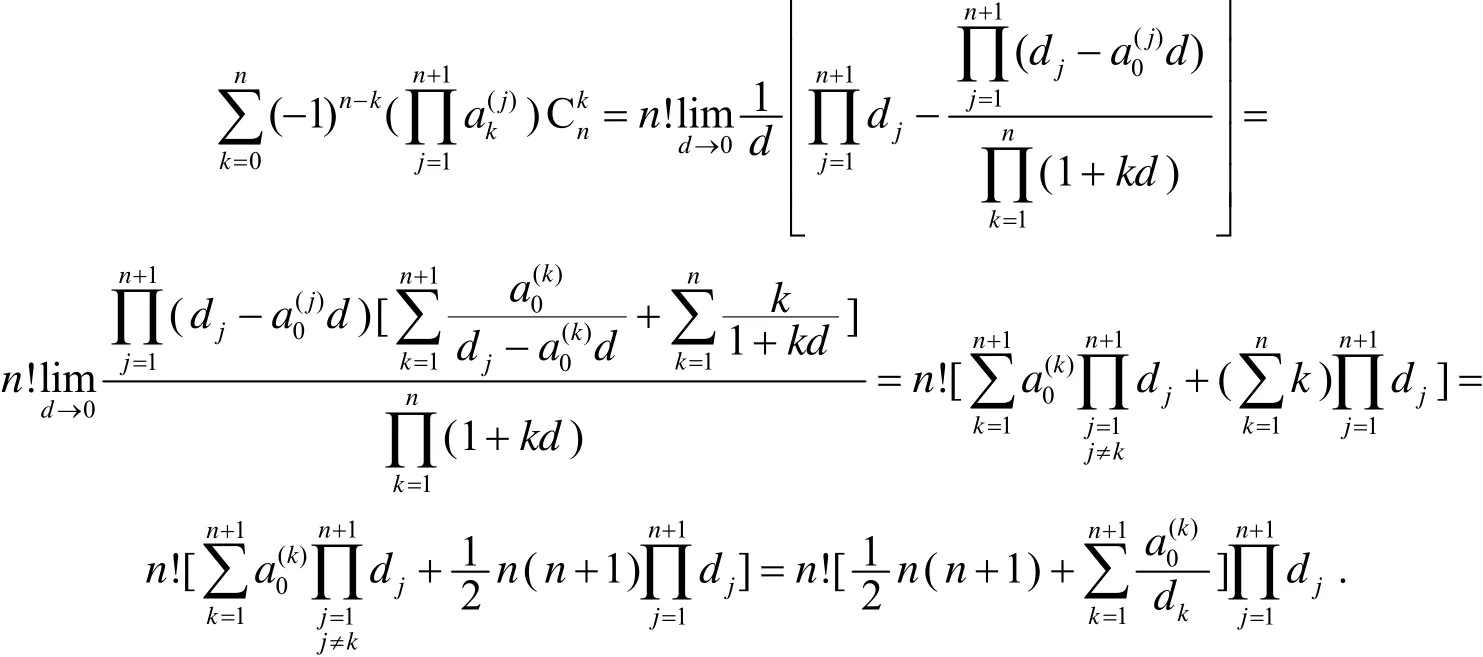

再设{ak}是公差为d的等差数列, 取则dj=d(j= 1, 2, …,n+1). 因
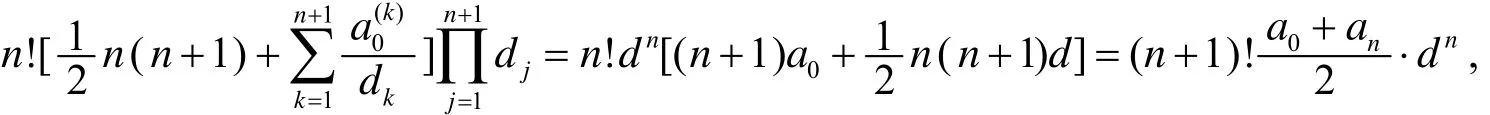
于是, 由(9)式, 有
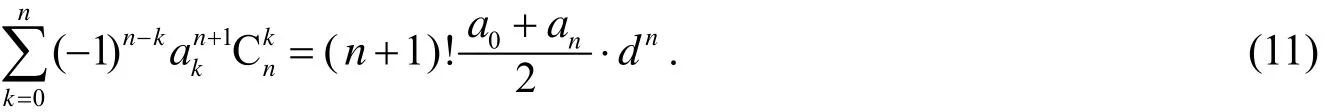
(10)、(11)两式即拙文[3]所证明的两个组合恒等式.
推论2设{bk}是公差分别为d1,d2,…,dm,d的等差数列, 且bk≠0(k= 1, 2, …,n),d≠0, 则当0≤m≤n时, 有
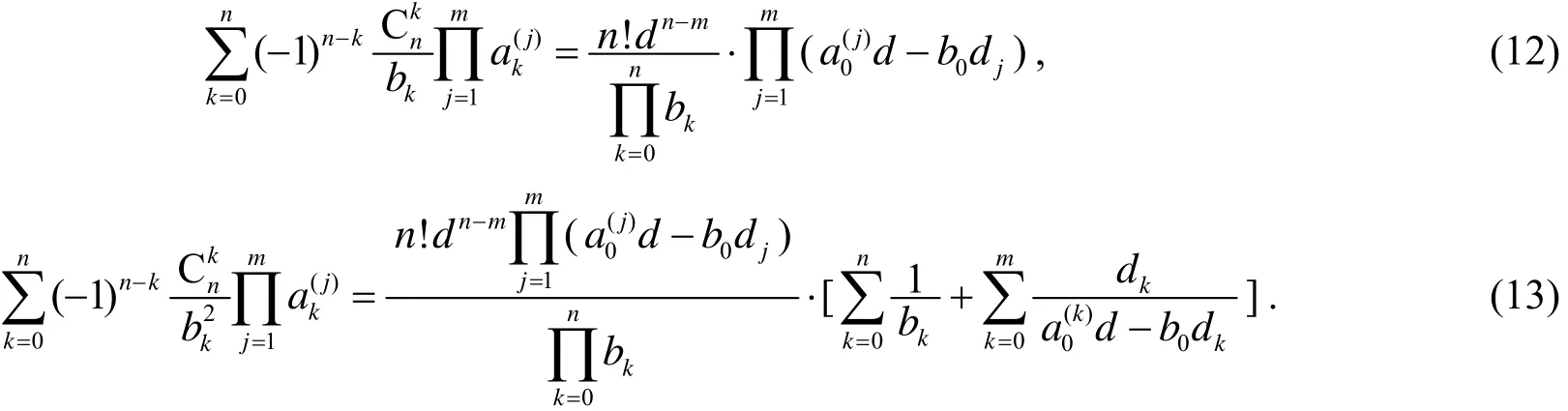
其中d0=1.
证明当d≠0时, 于定理中, 取=…==1(k= 1, 2, …,n), 则d=…=d=0, 于是由(3)、m+1n+1(4)两式即知(12)、(13)两式成立; 当d=0时, 由(10)式, 并注意当m=n时,dn−m=1即知(12)、(13)两式也成立.
推论3设{ak}, {bk}是公差分别为da,db的两个等差数列, 且bk≠0(k= 1, 2, …,n), 则当0≤m≤n时, 有
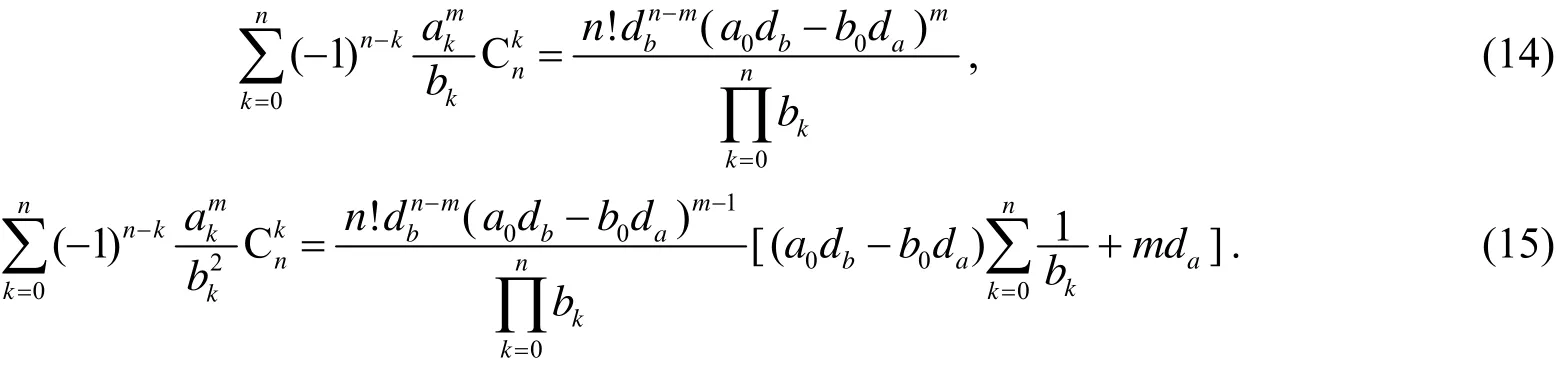
证明令=a(k= 0, 1, …,n), 则d=d=…=d=d, 且d=d, 于是, 由(12)、(14)两式即可得到(14)、(15)两式.
容易知道, 等式(14)、(15)推广了拙文[4]中的两个组合恒等式(原文(20)、(21)式):
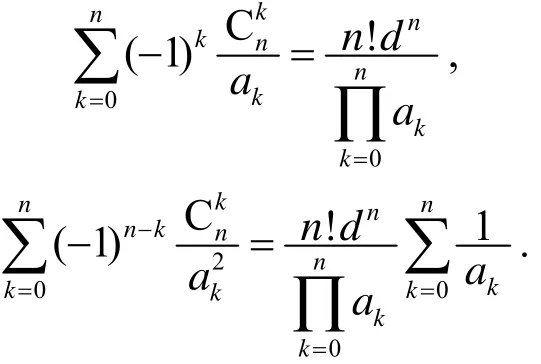
于(14)、(15)两式中, 取ak=k,bk=k+1(k= 0, 1, …,n), 则由da=db=1, 有
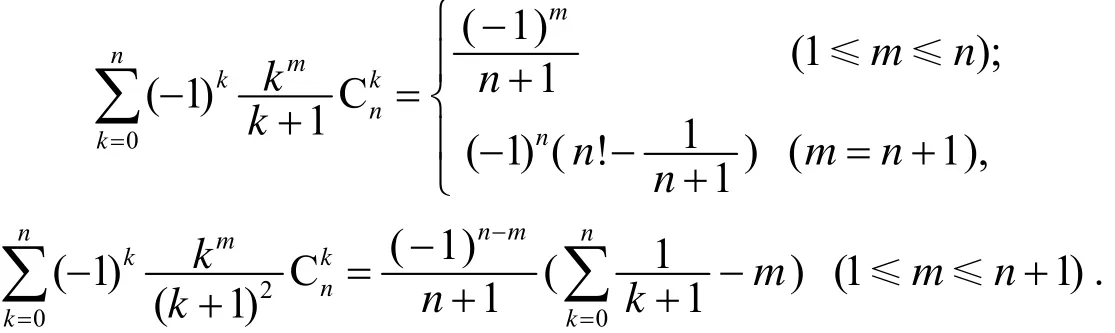
如果取ak=k,bk=2k+1(k= 0, 1,…,n), 则有
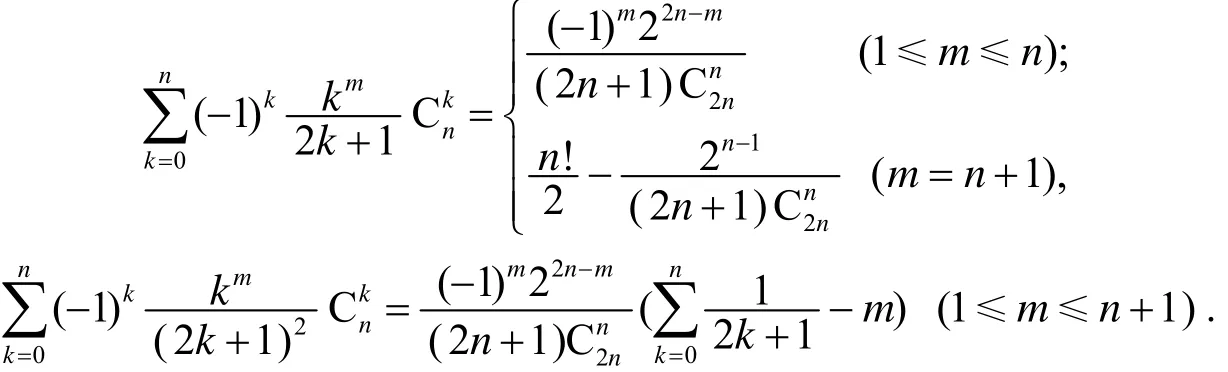
[1] 张禾瑞, 郝鈵新. 高等代数[M]. 第4版. 北京: 高等教育出版社, 1999: 65
[2] 欧阳光中, 朱学炎, 秦曾复. 数学分析(上册)[M]. 上海: 上海科学技术出版社, 1982: 185~187
[3] 萧振纲. 两类有趣的组合恒等式[J]. 数学通讯, 1994(1)
[4] 萧振纲. Vandermonde行列式的一个推广及其在初等数学中的应用[J]. 数学通报, 1994(9)
Two types of Combinatorial Identities Related to Arithmetic Sequence
XIAO Zhen-gang
(Hunan Institute of Science and Technology, Yueyang 414006, China)
In this paper, a polynomial was constructed ingeniously, and by using of the famous Lagrange's interpolation formul a and L'Hospital rule, two types of novel and profound combinatorial identities related to arithmetic sequence were deduced.
Lagrange's interpolation formula; arithmetic sequence; combinatorial identity
O122.7
A
1672-5298(2014)03-0014-04
2013-10-08
萧振纲(1957− ), 男, 湖南华容人, 湖南理工学院数学学院教授. 主要研究方向: 初等数学与竞赛数学

