浅层岩土室内、外热物性测试的相关性

高 平,张延军,2,方静涛,张 庆,李宏伟

1.吉林大学建设工程学院，长春 130026 2.吉林大学地下水资源与环境教育部重点实验室，长春 130021 3.吉林大学资产管理与后勤处，长春 130012

浅层岩土室内、外热物性测试的相关性

高 平1,张延军1,2,方静涛1,张 庆1,李宏伟3

1.吉林大学建设工程学院，长春 130026 2.吉林大学地下水资源与环境教育部重点实验室，长春 130021 3.吉林大学资产管理与后勤处，长春 130012

对于浅层岩土热物性参数测试中常用的实验室和现场热响应试验方法，结合上海某工程的实际情况，提出一种基于室内试验的岩土综合热物性参数确定方法。首先，根据室内、外试验测试结果的差异，选取地层厚度、含水率、密度及渗透系数作为影响二者热物性参数测试差异的主要因素，使用层次分析法确定各影响因素的权值，并按权值大小修正室内热物性参数测试结果。然后，分别模拟室外现场热响应试验和修正后的室内热物性参数以及实际地层的传热过程，得出三者在热量传导能力之间的差距分别为1.2%、1.1%及2.3%。最后，提出埋管深度和导热系数的乘积可代表岩土层的换热能力，且计算出修正后的室内热物性参数对应的均一导热系数与现场热响应试验测出的综合导热系数分别为1.832 W/(m·℃)和1.778 W/(m·℃)。

热物性参数；测试方法；层次分析法；相关性

0 引言

准确确定岩土层的热物性参数是科学应用地源热泵技术的关键之一，通过测定热物性参数以确定其热交换能力。主要的热物性参数包括导热系数、比热容和热扩散系数等，其中导热系数是衡量换热能力的关键参数。目前，热物性参数的测试主要有2种方法：实验室测试法和现场热响应试验法[1-2]。实验室测试法主要包括稳态热流法和非稳态热流法；现场热响应试验法是地源热泵领域广泛采用的一种测试岩土热物性参数的原位方法。然而，实验室测试不论是哪一种方法都存在明显的局限性，因为采集的岩土试样只能是局部深度的代表样品，其结构、含水量以及地下水流动对其导热的影响等均发生了变化，所测试的结果不能完全反映岩土层的换热能力。现场热响应试验是测试换热深度内整体岩土层热物性参数的平均值，它能够较真实地模拟地源热泵的实际运行情况[3]，测出的实验数据可以作为实际系统运行的数据，故利用该方法测试地下岩土体的热物性参数是进行换热器设计的最佳选择。不过，现场热响应试验也受许多因素的影响，如试验周期、供电稳定性、热损失或热增益等[4]。

以往的研究主要是针对现场热响应试验，如：于明志等[5]、管昌生等[6]对试验中用到的理论模型进行了研究；国内外研究人员考虑不同的影响因素，对现场测试仪器进行了改进和研发[1,7-9]；Lim等[10]、管昌生等[11]、胡平放等[3]对测试结果进行了不确定分析；Signorelli等[12]、Wanger等[13]对现场热响应试验进行过分析评价。然而，很少有针对实验室测试法测出的热物性参数的研究，仅有少数研究者指出其与现场热响应试验测出的热物性参数的差异及未考虑的因素[2,8,12,14-15]，对2种室内外热物性参数测试方法之间相关性的研究更少。

笔者结合上海地区某地块的热物性试验，深入分析研究在实验室中测试的热物性参数结果与现场热响应试验结果的区别。比较2种测试方法，分析实验室测试法中没有考虑的因素，而后选取影响热物性参数的主要因素。利用层次分析法[16]确定各个影响因素的权重，然后，按权值大小修正实验室测出的热物性参数，则变化后的数值能反映研究区地下岩土层的热传导能力。最后，利用课题组研发的地源热泵模拟程序模拟修正后的实验室测试的热物性参数与现场热响应试验测出的数值，验证二者在计算岩土体热量传导能力方面的作用基本相同，以说明该方法的适用性，并进一步与地埋管换热器的实际传热过程进行对比。通过对2种试验方法之间相关性的研究，可以更好地利用室内热物性参数，为地源热泵系统设计提供数据参考，其对室外现场热响应试验也是一种补充，进而可以部分替代热响应试验。

1 基本原理

一般来说，在取岩土样品的过程中，其结构、含水量等总会受到影响，使导热系数与实际情况总是有较大的出入，故在地源热泵设计中基本采用现场热响应试验的结果。根据这些情况，笔者提出一种方法：考虑主要影响因素，采用层次分析法修正室内测出的数据，反演导热系数，可以取得与现场热响应试验相近的测试结果。

每个影响热物性参数的因素对其影响程度均不同，如：比热容对导热系数造成的误差很小[17],但随着含水率、密度的逐渐增大，其对导热系数的影响却逐渐变大;而密度与孔隙率密切相关，但影响却与之相反[18-19]；地下水渗流对导热系数的影响更明显[14,20-23]。结合以往的研究成果，本文的研究思路如下：

1)不同地层的厚度、含水率、密度及渗透系数作为影响室内外试验热物性参数差异的主要因素；

2)开展详尽的野外勘探、现场热响应试验及室内测试，取得准确的岩土热物性参数、物理参数及岩性资料；

3)采用层次分析法建立导热系数的层次结构模型，确定影响因素的权重值；

4)利用热传导模型和渗流模型模拟修正前后的导热系数及实际情况下的地下岩土层的换热能力，以验证本文提出方法的可行性。

1.1 层次分析法

运用层次分析法进行导热系数影响因素权重分析可分为3个阶段[24]。首先，采用Saaty[16]建议的1-9标度法构造出n×n阶的判断矩阵A：

(1)

式中：aij为因素i相对于因素j的重要程度。

然后，分别计算因素权向量ω、最大特征值λmax和随机一致性比率CR：

(2)

(3)

(4)

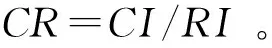
(5)

式中：ωi为因素权重值；n为矩阵阶数；CI为一致性指标；RI为平均随机一致性指标，见表1。

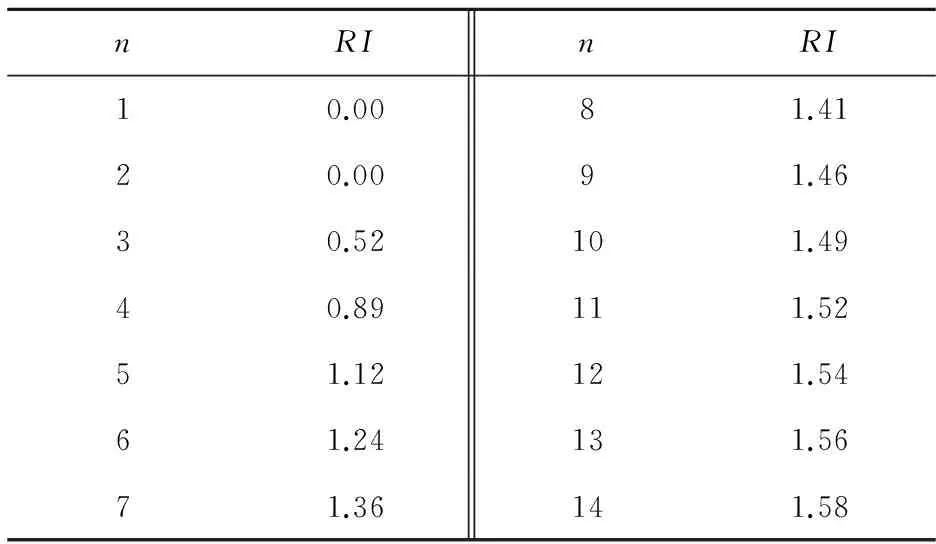
表1 平均随机一致性指标

最后，通过式(6)、(7)计算层次总排序及对应的一致性比率。

(6)

(7)

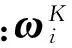
对于计算出的权值，采用热传导模型模拟现场热响应试验和修正前后的室内实验的热物性参数。

1.2 传热数学模型

为了模拟地下换热器在岩土层中的实际传热过程，必须建立完备的地埋管传热数学模型。其中，热质运移的对流-弥散传热过程，类似溶质的运移机理，并可以借助达西定律、质量守恒原理及多孔介质理论。该过程涉及到传热传质多种因素，要建立完备的耦合理论模型是相当困难的，故需要做很多的简化来建立理论模型进行数值求解。

热质运移方程如下：

(8)

式中：ε为含水层介质有效孔隙度；ρf为流体密度，kg/m3；cf为流体比热容，J/(kg·℃)；cs为孔隙介质比热容，J/(kg·℃)；ρs为孔隙介质密度，kg/m3；λf为流体热导率，W/(m·℃)；λs为孔隙介质导热系数，W/(m·℃)；DH为热动力弥散系数张量，W/(m·℃)；T为单元体内两相介质的温度，℃；I为3阶单位矩阵；ρ*为流体源项密度，kg/m3；T*为流体源项的温度，℃；q为流体源汇项强度，流入为正，流出为负，m3/(m3·s)；v为流体速度向量，m/s；qH为热源强度，W/m3。

地下水流动的偏微分方程为

(9)

式中：p为流体的压力，Pa；k为多孔介质的渗透率张量，m2；μ为动力黏滞系数，kg/(m·s)；g为重力加速度，m/s2；t为时间，s。

2 工程实例验证

2.1 工程概况

上海某工程的用地面积为50 578 m2，总建筑面积约122 988 m2，其中，地上建筑面积约615 93 m2，地下建筑面积约613 95 m2。

为了应用地源热泵技术，在该地区进行了岩土热物性测试，包括3个孔，共计6个工况的现场热响应试验测试，以及1#孔的15个原状岩土样品的室内热物性测试。现场热响应试验结果如表2所示。

根据野外钻探结果，该地区自然地面以下100 m深度范围内所揭示的地基土主要以黏土、粉土及砂土为主。参考钻孔岩性资料，将该研究区100 m深度范围内的地基土从上到下概化为淤泥质黏土(15 m)、粉质黏土(15 m)、黏土(30 m)及砂土(40 m)4种类型。另外，研究区内揭示有潜水含水层及承压含水层，地下水流速一般为1.2～1.5 cm/d，同时受场地周边降水、排水等因素的影响。

2.2 层次分析法确定权重

2.2.1 建立导热系数分析的递阶层次结构模型

根据影响导热系数的主要因素，结合上海某地区的地质条件和测试结果，组成导热系数的主要地层类型为淤泥质黏土、黏土、粉质黏土以及砂土，而影响各类型土导热系数差别的主要因素为地层厚度、含水率、地层密度及渗透系数,则导热系数分析的递阶层次结构模型如图1所示。

2.2.2 构造判断矩阵及确定权重并进行一致性检验

对准则层的因素两两比较，并咨询相关专家的意见及参考以往研究成果，综合分析各种情况确定目标层对准则层影响因素的导热系数判断矩阵A：

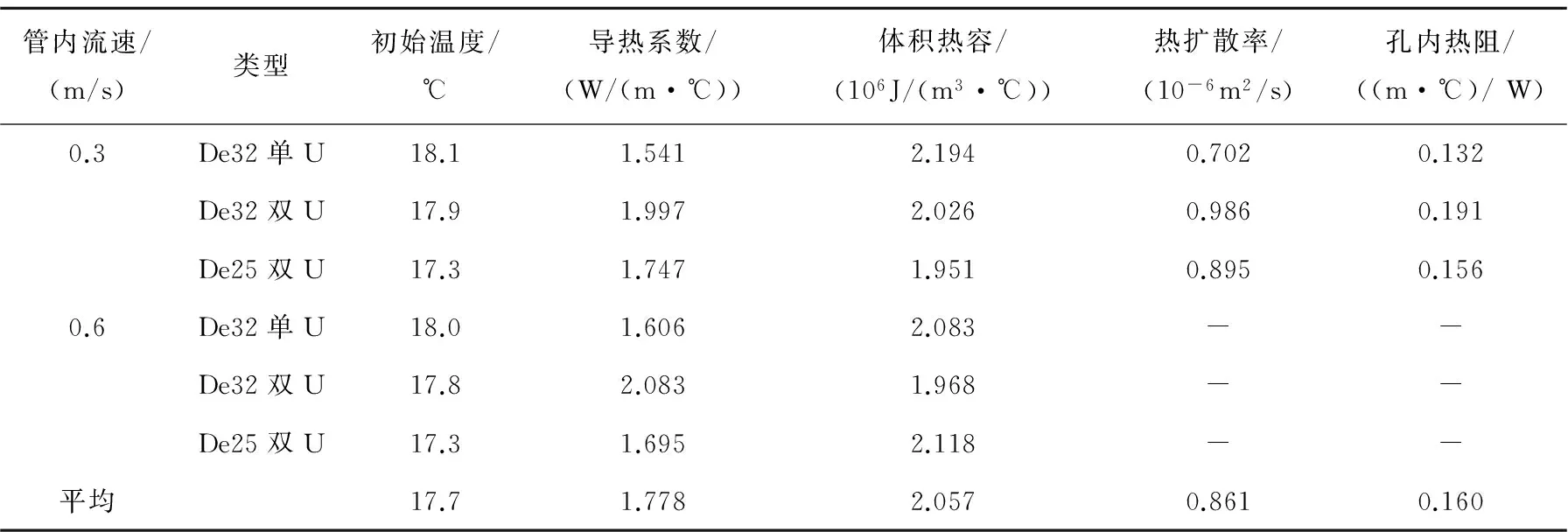
(10)

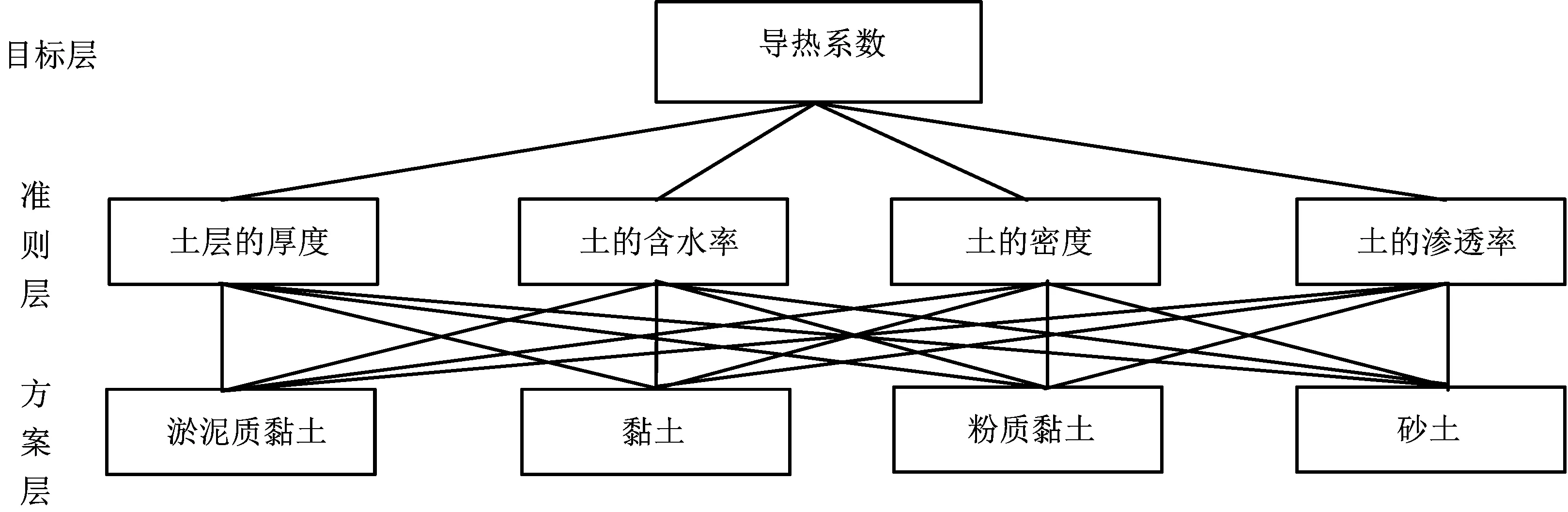
图1 导热系数分析的递阶层次结构模型Fig.1 Hierarchical structure model of thermal conductivity analysis

根据式(2)计算土层的厚度、土的含水率、密度及渗透率的权重值分别为0.470 8、0.171 5、0.073 6及0.284 1。

根据式(10)求得最大特征值以及偏离一致性指标，代入式(5)可得随机一致性比例：

CR=0.02<0.10 。

因此，判断矩阵A满足一致性要求。

同理，可以构造准则层对方案层的判断矩阵，并计算权重且进行一致性检验，得出各个判断矩阵的权重值，见表3。最后根据综合权重的计算公式(6)，得出各类型土在影响导热系数方面所占的比例，这些判断矩阵均经过检验，满足一致性要求。淤泥质黏土、黏土、粉质黏土及砂土的综合权重值分别为0.183 5、0.226 6、0.183 7及0.406 2。可以看出，权重值最大的是砂土，而淤泥质黏土、粉质黏土的权重值基本相同，黏土的权重值比二者稍大。这是因为砂土的孔隙连通性较好，渗透性强，有利于热量的传递，而其他3种土虽然孔隙比较大，但是孔隙的连通性较差，不利于热量的传递。

表3 各影响因素判断矩阵的权重值

Table 3 Weighted values of every influencing factor judgment matrixes

判断矩阵ω1ω2ω3ω4土层的厚度0.14120.26530.14120.4545土的含水率0.46580.27710.16110.0960土的密度0.14110.14110.26310.4547土的渗透率0.09410.15780.24710.5010

2.3 模型验证

研究区的岩土层较稳定，初始温度平均为17.7 ℃。此次现场热响应试验中，3个钻孔直径皆为150 mm，钻孔深度均在100 m左右，分别采用单U及双U型地埋管，管外径为32 mm，管内径为26 mm。将各个岩土层的热物性参数进行均一化并根据上述计算出的权重值，计算修正后的室内测出的导热系数和热扩散率，见表4。

为了验证计算出的权重值的正确性，根据工程的实际情况，在不影响模拟精度和能得出相对准确模拟结果的情况下，建立U型地埋管换热器的数值模型，来模拟权重修正后的室内测出的导热系数与现场热响应试验的在地下岩土层中的热传导能力，具体的模型建立如下。

1)数值模型：模型示意图如图2所示，宽度为5 m，深度为100 m，从上到下依次分为淤泥质黏土层(15 m)、粉质黏土层(15 m)、黏土层(30 m)及砂土层(40 m)。

2)初始条件：初始温度为17.7 ℃，不考虑季节变化的影响。

3)边界条件：假定四周边界均为定温度边界，上部和底部为隔热边界。

4)网格剖分：在本模型中，z方向坐标向下，采用均匀网格的剖分方法。

5)其他设置：热源设置在模拟区域的中心节点上，其埋管深度为95 m，模拟夏季连续运行工况，负荷为3.5 kW；时间总长度为259 200 s，即为3 d。

根据上述建立的U型地埋管换热器的数值模型，分别对现场热响应试验和室内测出的热物性参数及权值修正后的室内热物性参数分别进行模拟。在模拟现场热响应试验时，采用的是均一土层及现场测出的热物性参数，见表2；而在模拟室内实验时的热物性参数取上述4种类型土的平均值，见表4。模拟结果云图见图3、图4。

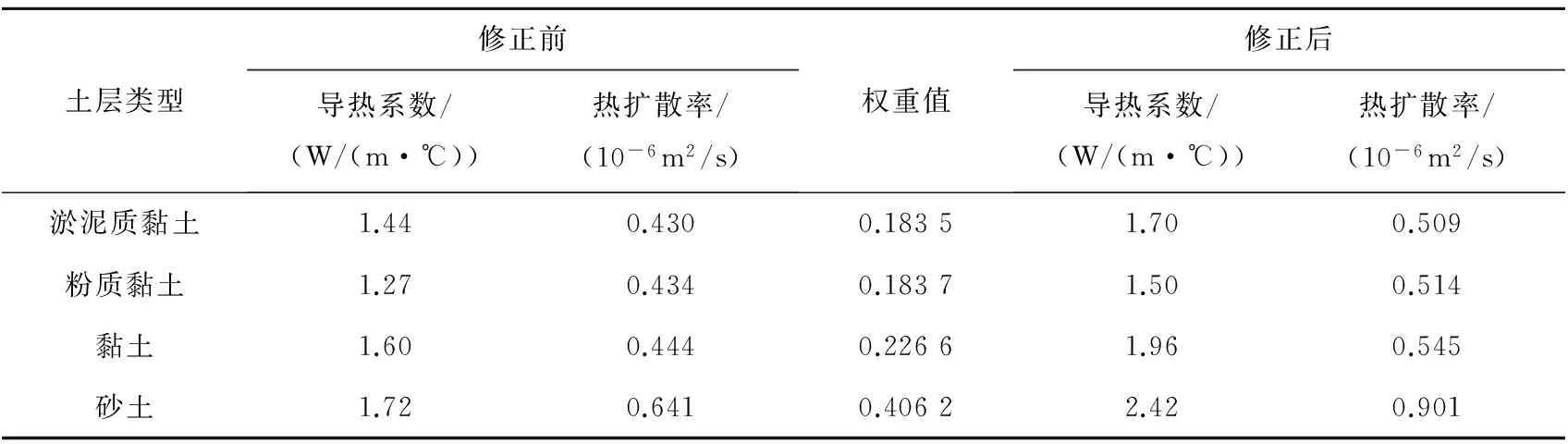
表4 修正前后室内实验的热物性参数

图2 数值模型示意图Fig.2 Diagram of numerical model

从图3中可以看出，在模拟现场热响应实验时，热量沿中心热源向四周均匀扩散，地下温度场的分布变化以热源为中心对称分布。选取x=2 m截面，如图中红线所示，即与中心热源距离约为0.5 m的截面，在模拟深度范围内，通过该截面的总热流量Q=1 606.9 J/(m·s)。

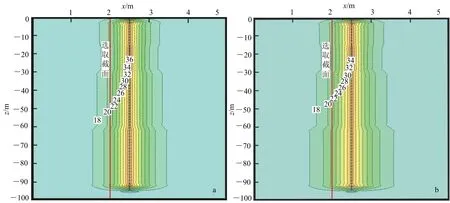
a.修正前；b修正后。图4 室内实验模拟结果云图Fig.4 Contour of indoor experiments numerical results

图3 现场热响应实验模拟结果云图Fig.3 Contour of field thermal response tests numerical results

从图4a中可以看出，与图3明显不同，地下温度场分为4个部分，这是因为淤泥质黏土、粉质黏土、黏土及砂土等4种土的热物性参数不同；可以看出，随着导热系数增大，其热量向四周岩土层传递的越多，反之，热量在热源附近积累，但每部分温度场依然以热源为中心对称分布，热量均匀地向四周岩土层扩散。通过上述截面的Q=1 356.4 J/(m·s)，与图3相差15.6%，这只是该截面的差值，对于整个研究区，整个热量差值会更大，说明室内测出的岩土热物性参数仅能反映一定的热传导能力，与实际情况差距较大。

从图4b可以看出，与图4a相似，其地下温度场也分成4部分，在考虑土层厚度、土的含水率、土的密度及土的渗透率等影响因素后，各土层的导热系数增大，因此热量向周围岩土层传递得较多，通过上述截面的Q=1 587.7 J/(m·s)，与图3仅相差1.2%，即使考虑整个研究区域，其热量差值也基本相同，误差能满足工程设计的要求，说明在考虑主要影响因素后，修正后的导热系数基本能反映岩土层的换热能力。

为了模拟地源热泵的实际传热过程，根据工程的实际情况，建立一个U型地埋管换热器的数值模型，模型的建立过程与上面相似。只是考虑地下水渗流的影响，在砂土层位加入了从右向左的地下水流，具体模型示意图如图5所示。根据现场的抽灌水试验，地下水的渗流速度为1.73×10-7m/s；地下水的平均温度、导热系数、比热容、黏度及膨胀系数分别为18.02 ℃、0.6 W/(m·℃)、4.182 kJ/kg、0.001 Pa·s及0.000 2 /℃。而根据工程的热物性试验和土的物理力学性质实验，将各地层的参数进行平均得到模拟所需的参数，见表5。

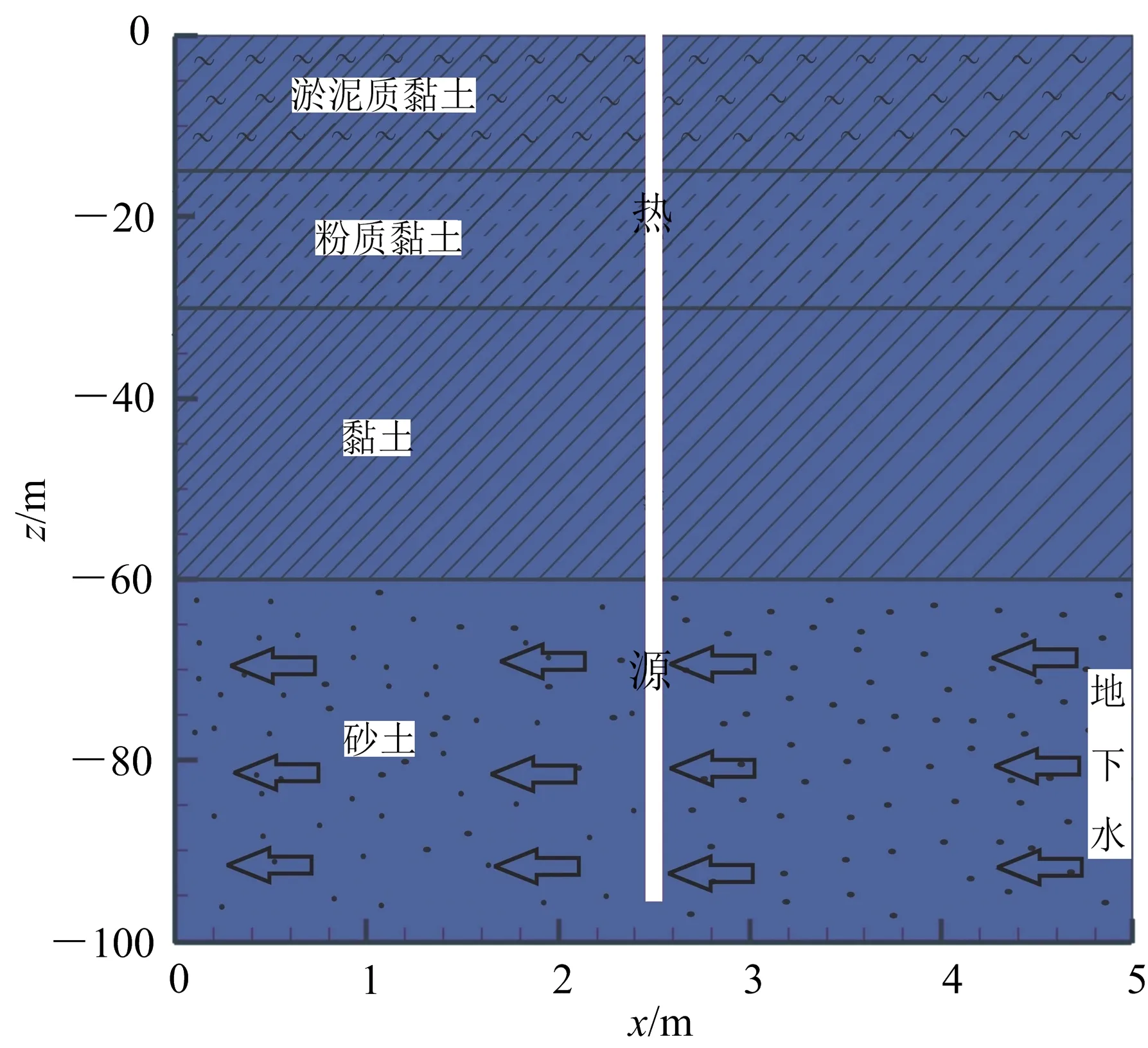
图5 数值模型示意图Fig.5 Diagram of numerical model

根据上述建立的数值模型，对地源热泵的实际传热过程进行模拟，得出地下温度场的变化结果，地埋管周围的岩土层温度场的变化云图见图6。可以看出：上部土层在无地下水流动的影响时，温度场的分布变化基本上是沿着垂直U型地埋管换热器对称分布，这说明地埋管换热器的传热与周围岩土体的换热是以U型地埋管为轴线向四周均匀传热的；下部砂土层有地下水渗流的存在，温度场受水流的影响不再以垂直U型地埋管换热器为中心成对称分布，而是沿水流方向有所偏移，在地下水渗流的影响下，地层温度有所降低。与图3、图4b类似，该图通过x=2 m这个截面的Q=1 624.8 J/(m·s)；该截面的热流量与图3、图4b之间的差距分别为1.1%及2.3%，说明三者在地下岩土层热量传递方面的能力相同，进一步验证了本文修正方法的可行性。

表5 岩土层热物性参数

Table 5 Thermal physical parameters of geotechnical layers

土层类型ερ/(kg/m3)λ/(W/(m·℃))a/(10-6m2/s)c/(kJ/m3)淤泥质黏土0.5417901.440.4303349粉质黏土0.5118301.270.4342926黏土0.4419451.600.4443604砂土0.4020001.720.6412683

注：ρ为密度；c为比热容；λ为导热系数；a为热扩散率。

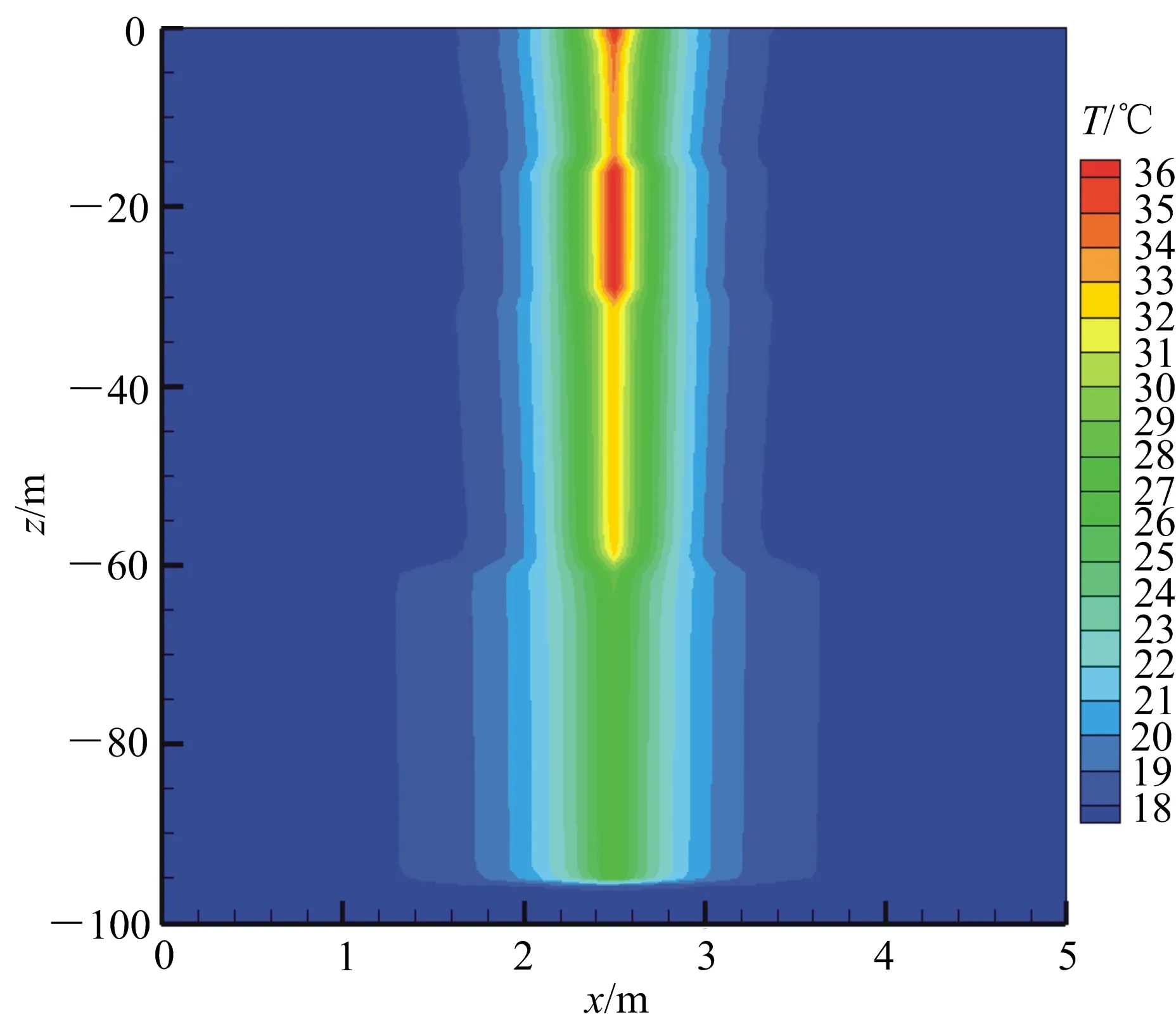
图6 地埋管换热器周围温度场云图Fig.6 Contour of temperature field around underground heat exchanger

另外，在地源热泵系统工程设计中，其所涉及的关键设计参数为埋管深度和导热系数，二者的乘积可代表其换热能力。对于现场热响应试验而言，K0=Hλ=177.80 W/℃。其中，H为岩土层的总厚度，m。

修正后的室内实验测试的导热系数，见表4，为各层的导热系数与各层厚度乘积之和。从上面的研究可以得出，该值在理论上应该接近现场热响应试验结果，但由于各种地质、测试等因素影响，笔者建议再乘以一个系数(1-η)，其与计算模型概化程度有关：

(9)

其中：λ*为修正后的均一导热系数，W/(m·℃)；h1,…,hn为岩土层中概化后各层的层厚，m；λ1,…,λn为各岩土层对应的导热系数，W/(m·℃)；η=0.01～0.15为修正系数，与地基土概化的简易程度有关，概化越简单，其数值越高。于是，

对应的λ*=1.832 W/(m·℃)，与现场热响应试验的λ=1.778 W/(m·℃)基本相同，这样就可以方便用于工程设计。

3 结论

1)对比室内热物性测试与现场热响应试验之间的差异，并结合上海某地区的实际情况，提出影响二者的主要因素为土层厚度、土的含水率、土的密度及土的渗透率。

2)结合上海地区某地块的热物性试验，运用层次分析法确定出淤泥质黏土、粉质黏土、黏土及砂土对综合导热系数的权重分别为0.183 5、0.183 7、0.226 6、0.406 2。

3)对现场热响应试验及修正后的室内热物性实验分别进行模拟，得出相同截面的热量差异仅为1.2%；采用课题组研发的地源热泵模拟程序，模拟地源热泵的实际传热情况，得出相同截面的热流量与现场热响应实验及修正后的室内热物性实验之间的差距分别为1.1%及2.3%，说明三者在热量运移方面的能力基本相同，验证了本文修正方法的可行性。

4)在地源热泵工程设计中，关键设计参数为埋管深度和导热系数，其二者的乘积可代表其换热能力，对于修正后的室内热物性参数，其乘积为183.24 W/℃，对应的均一导热系数1.832 W/(m·℃)，与现场热响应试验测出的综合导热系数1.778 W/(m·℃)基本相同。

本文提出的方法是对现场热响应试验的较好补充，可以在一定程度上代替现场热响应试验。但由于该方法的提出基于上海地区某地块的热物性实验，对于其他地区的适用性需要做进一步的研究。

[1] 王书中，由世俊，张光平.热响应测试在土壤热交换器设计中的应用[J].太阳能学报，2007，28(4)：405-410. Wang Shuzhong，You Shijun，Zhang Guangping. Application of Geo-Thermal Response Test in the Design of Ground Heat Exchanger[J]. Acta Energiae Solaris Sinica，2007，28(4)：405-410.

[2] 张庆，张延军，周炳强，等.天然冷源对地下水源热泵的影响规律[J].吉林大学学报：地球科学版，2013，43(2)：537-549. Zhang Qing, Zhang Yanjun, Zhou Bingqiang, et al. Influence of Nature Cold Source on Groundwater Heat Source Pump[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(2)：537-549.

[3] 胡平放，孟庆丰，管昌生，等.岩土综合热物性参数的不确定性分析[J].湖南大学学报：自然科学版，2009，36(12)：35-39. Hu Pingfang，Meng Qingfeng，Guan Changsheng，et al. Uncertainty Analysis on the Parameters of the Rock-Soil Thermal Properties[J]. Journal of Hunan University: Natural Sciences，2009，36(12)：35-39.

[4] 宋欣阳.用于地源热泵系统现场热响应测试的土壤热物性实验研究[D].天津：天津大学，2009. Song Xinyang. The Experimental Research on Thermo-Physical Properties of the Soils for the In-Site Thermal Response Test of Ground Source Heat Pump System[D]. Tianjin：Tianjin University，2009.

[5] 于明志，彭晓峰，方肇洪，等.基于线热源模型的地下岩土热物性测试方法[J].太阳能学报，2006，27(3)：280-283. Yu Mingzhi，Peng Xiaofeng，Fang Zhaohong，et al. Line Source Method for Measuring Thermal Properties of Deep Ground[J]. Acta Energiae Solaris Sinica，2006，27(3)：280-283.

[6] 管昌生，万兆，胡平放.地源热泵地埋管多层岩土温度场的数值分析[J].武汉工程大学学报，2011，33(4)：42-45. Guan Changsheng，Wan Zhao，Hu Pingfang. Numerical Analysis on Multilayer Geotechnical Temperature Field of GSHP Buried Tube[J]. Journal of Wuhan Institute of Technology，2011，33(4)：42-45.

[7] 孟祥瑞.便携式地层热物性原位测试仪的研究及应用[D].长春：吉林大学，2011. Meng Xiangrui. Application and Research on Portable Device for In-Situ Testing Strata Thermo-Physical Properties[D].Changchun：Jilin University，2012.

[8] 王华军，齐承英，王恩宇，等.土壤热响应特性的一种改进实验装置[J].太阳能学报，2010，31(5)：615-619. Wang Huajun，Qi Chengying，Wang Enyu，et al. Improved Equipment of Thermal Response Test of Rock Soils[J]. Acta Energiae Solaris Sinica，2010，31(5)：615-619.

[9] Gehlin S. Thermal Response Test-Method Develo-pment and Evaluation[D]. Sweden：Lule? University of Technology，2002.

[10] Lim K， Lee S， Lee C. An Experimental Study on the Thermal Performance of Ground Heat Exchanger[J]. Experimental Thermal and Fluid Science，2007，31(8)：985-990.

[11] 管昌生，刘卓栋，陈绪义. 地源热泵换热器随机因素分析与可靠性设计方法[J].建筑热能通风空调，2009，28(1)：46-49. Guan Changsheng，Liu Zhuodong，Chen Xuyi. Analysis of Random Factors and Reliability Design Method of Geothermal Heat Exchanger[J]. Building Energy & Environment，2009，28(1)：46-49.

[12] Signorelli S,Bassetti S.Numerical Evaluation of Ther-mal Response Tests[J]. Geothermics，2007，36(2)：141-166.

[13] Wanger R，Clauser C. Evaluating Thermal Response Tests Using Parameter Estimation for Thermal Conductivity and Thermal Capacity[J]. Journal of Geophysics and Engineering，2005，2(4)：349-356.

[14] 范蕊，马最良，姚杨，等.地下水流动对地下埋管换热器影响的实验研究[J].太阳能学报，2007，28(8)：874-880. Fan Rui，Ma Zuiliang，Yao Yang，et al. Experimental Research on Influence of Groundwater Advection on Performance of GHE[J]. Acta Energiae Solaris Sinica，2007，28(8)：874-880.

[15] 于明志，方肇洪.现场测量深层岩土热物性方法[J].工程热物理学报2002，23(3)：354-356. Yu Mingzhi，Fang Zhaohong. A Method for in Situ Determining the Thermal Properties of Deep Ground[J]. Journal of Engineering Thermophysics，2002，23(3)：354-356.

[16] Saaty T L. The Analytic Hierarchy Process[J]. Strategic Management Journal，1980(9)：22-71.

[17] 李朝佳.浅层岩土热物性参数测试试验与研究[D].长春：吉林大学，2009. Li Zhaojia. Research and Testing Experiment of Thermal Parameters of Shallow Layer Soil and Rock[D]. Changchun：Jilin University，2009.

[18] Abu-Hamdeh H N. Thermal Properties of Soils as Affected by Density and Water Content[J]. Biosystems Engineering，2003，86(1)：97-102.

[19] 肖琳，李晓昭，赵晓豹，等.含水量与孔隙率对土体热导率影响的室内实验[J].解放军理工大学学报：自然科学版，2008，9(3)：241-247. Xiao Lin，Li Xiaozhao，Zhao Xiaobao，et al. Laboratory on Influence of Moisture Content and Porosity on Thermal Conductivity of Soils[J]. Journal of PLA University of Science and Technology：Natural Science Edition，2008，9(3)：241-247.

[20] 范蕊，马最良.地下水流动对地下管群换热器传热的影响分析[J].太阳能学报，2006，27(11)：1155-1162. Fan Rui，Ma Zuiliang. Heat Transfer Analysis of Geothermal Heat Exchanger Under Coupled Condition and Groundwater Advection[J]. Acta Energiae Solaris Sinica，2006，27(11)：1155-1162.

[21] Chiasson A D，Rees S J，Spitler J D. A Preliminary Assessment of the Effects of Ground Water Flow on Closed-Loop Ground Source Heat Pump System[J]. ASHRAE Transactions，2000，106(1)：380-393.

[22] 陆观立.地下水渗流对土壤源热泵地埋管换热特性影响研究[D].成都：西南交通大学，2009. Lu Guanli. Study of Effect of Groundwater Seepage on Characteristic of Heat Transfer in Ground Source Heat Pump System[D]. Chengdu：Southwest Jiaotong University，2009.

[23] 王中华.地下水渗流下地埋管换热器的数值模拟分析[D].广州：华南理工大学，2011. Wang Zhonghua. Numerical Simulation of Under-Ground Heat Exchanger Under Groundwater Advection Conditions[D]. Guangzhou：South China University of Technology，2011.

[24] 汪应洛.系统工程[M].北京：机械工业出版社，2003. Wang Yingluo. System Engineering[M]. Beijing：Mechanics Industry Press，2003.

Correlation of Shallow Layer Rock and Soil Thermal Physical Tests in Laboratory and Field

Gao Ping1，Zhang Yanjun1,2，Fang Jingtao1，Zhang Qing1，Li Hongwei3

1.CollegeofConstructionalEngineering，JilinUniversity，Changchun130026，China2.MinistryofEducationKeyLaboratoryofGroundwaterResourcesandEnvironment，JilinUniversity，Changchun130021，China3.AssetManagementandLogisticsDepartment，JilinUniversity，Changchun130012，China

The authors propose a method to determine synthetically geotechnical thermal physical parameters according to laboratory experiments for a certain project in Shanghai. Based on discrepancy of testing results between laboratory and field test，formation thickness，water ratio，density and osmotic coefficient are chosen as primary factors that affect difference of thermal physical parameters between laboratory testing and field testing. And the weighted values of every factor are determined using analytic hierarchy process (AHP)，which are used to modify testing results of thermal physical parameters in laboratory. Furthermore the authors simulate field and modified laboratory thermal physical parameters simulates and practically heat transferring，respectively.It shows that the discrepancy of heat conduction capacity are 1.2%，1.1% and 2.3% for three conditions. The heat transfer capacity can be reoresented by the value of product of pipe depth multiplied by thermal conductivity. Uniform thermal conductivity computed by modified parameters of laboratory is basically equal to comprehensive thermal conductivity tested by field thermal response test，which are 1.832 W/(m·℃) and 1.778 W/(m·℃) respectively.

thermal physical parameters; testing method; analytic hierarchy process; correlation

10.13278/j.cnki.jjuese.201401203.

2013-05-06

国家“863”计划项目(2012AA052803)；国家自然科学基金项目(40972172,41372239)；高等学校博士学科点专项科研基金项目(20110061110055)

高平(1987-)，男，博士研究生，主要从事岩土热力学研究，E-mail:gaoping12@mails.jlu.edu.cn

张延军(1968-)，男，教授，博士生导师，主要从事岩土多场耦合研究，E-mail:zhangyanj@jlu.edu.cn。

10.13278/j.cnki.jjuese.201401203

P641.139;TK521

A

高平,张延军,方静涛,等.浅层岩土室内、外热物性测试的相关性.吉林大学学报:地球科学版,2014,44(1):259-267.

Gao Ping，Zhang Yanjun，Fang Jingtao，et al.Correlation of Shallow Layer Rock and Soil Thermal Physical Tests in Laboratory and Field.Journal of Jilin University:Earth Science Edition,2014,44(1):259-267.doi:10.13278/j.cnki.jjuese.201401203.