大地电磁场三维地形影响的矢量有限元数值模拟

顾观文，吴文鹂，李桐林

1.吉林大学地球探测科学与技术学院，长春 130061 2.中国地质科学院地球物理地球化学勘查研究所，河北 廊坊 065000

大地电磁场三维地形影响的矢量有限元数值模拟

顾观文1, 2，吴文鹂2，李桐林1

1.吉林大学地球探测科学与技术学院，长春 130061 2.中国地质科学院地球物理地球化学勘查研究所，河北 廊坊 065000

地形对大地电磁场的影响规律研究对于实际大地电磁测深反演解释具有重要的意义。基于矢量有限元法进行了大地电磁三维地形响应数值模拟。首先与二维地形模拟结果比较，验证了算法的正确性；接着，分别对1个山峰地形和1个山谷地形进行了模拟；最后，比较了二维模拟与三维模拟结果。结果表明：三维阻抗张量的Zxy模式和Zyx模式都会受到地形影响；用二维地形模拟结果去近似三维地形响应，二维TE模式与真实三维响应结果差别很大，TM模式接近真实三维响应结果；如采用二维反演处理带地形的三维MT数据，TM极化模式反演更为合理。

大地电磁；三维地形；数值模拟；矢量有限元法

0 引言

地形会对大地电磁信号产生很大的干扰，在地形复杂地区进行电磁勘探时，必需考虑地形的影响，所以用数值方法模拟计算地形对大地电磁信号的影响非常重要。为此，国内外在这方面已有不少研究:Chouteau等[1]和Wannamaker等[2]用有限元法模拟了二维地形对大地电磁测深信号的影响；赵广茂等[3]基于二次场实现了二维起伏地形大地电磁响应的有限元数值模拟；徐世浙等[4]、阮百尧等[5]采用边界元法模拟三维地形大地电磁场；Chen等[6]基于有限差分法模拟三维地形的大地电磁响应；Baba等[7]将FS(flat seafloor)技术结合Mackie等[8]的大地电磁三维有限差分模拟技术实现了海底起伏地形下的三维数值模拟；Sasaki[9]采用交错网格有限差分法模拟了三维山丘地形的大地电磁响应。

矢量有限单元法在地球物理电磁法领域的应用研究起步较晚，但近十年在大地电磁三维数值模拟中的应用取得了比较大的进展。2002年，Yoshimura等[10]利用矢量有限单元法对一系列频率的大地电磁场响应进行了数值模拟，并与交错网格有限差分法的计算结果进行了对比；2004年，Mitsuhata等[11]将磁场分解为电场矢量势和磁场标量势，并利用矢量有限单元法和节点有限单元法相结合的方法对大地电磁场进行了三维数值模拟；同年，Shi等[12]研究了结合散度校正的大地电磁法矢量有限单元法三维正演；2007年，Jin Nam Nyung[13]等基于棱边有限元法模拟了MT(magnetotelluric)三维地形响应；2008年Liu等[14]和2010年刘长生等[15]基于非结构化四面体网格的H型自适应矢量有限元法对大地电磁场进行了三维正演。

在前人[11-13]研究基础上，笔者采用矢量有限元法模拟大地电磁场三维地形影响。首先研究矢量有限元算法，然后通过与山脊地形二维模拟结果比较，验证算法的正确性。为了研究三维地形的影响，分别对1个三维山峰地形和1个山谷地形进行模拟，分析地形对两种极化模式的影响；通过与相应的二维地形模拟结果比较，讨论用二维地形模拟结果去近似三维地形响应的情况。

1 三维矢量有限元正演模拟算法

1.1 基本理论

在大地电磁研究的频率范围内(10-4～103Hz)忽略位移电流的作用。取时谐场为e-iωt，麦克斯韦方程组的微分形式表示如下：

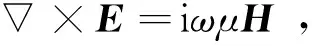
(1a)

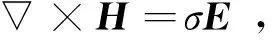
(1b)

(1c)

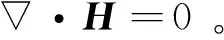
(1d)

式中：E是电场强度矢量；H是磁场强度矢量；σ是介质的电导率；μ是介质的磁导率；ε是介质的介电常数；ρf是自由电荷密度函数。对式(1a)两边取旋度，再将式(1b)代入到式(1a)，则将电磁场满足的一阶微分方程变为二阶微分方程，可以得到E满足如下方程：

(2)

这是3个电场分量相互耦合在一起的方程式。求解偏微分方程组(2)得到电场分量Ex、Ey、Ez的分布后，可以根据式(1a)求得磁场分量Hx、Hy、Hz的分布。

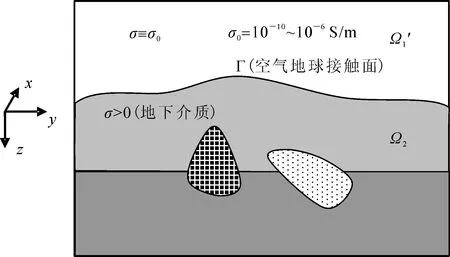
图1 带地形的三维MT数值模拟区域剖面示意图Fig. 1 Profile of the numerical modeling domain for 3D MT with topography

将式(2)写成

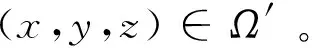
(3)

取第一类边界条件

(4)

其中,g是边界上的矢量电场，可以采用一维或者二维MT计算值[16-18]。这样，式(3)和式(4)构成了大地电磁三维正演的边值问题。

1.2 矢量有限元分析

有限元法求解上述区域(图1)的电磁场问题，需要将研究区域离散化，即对研究区域进行六面体网格剖分(图2a)。沿x、y和z轴方向分别剖分成Nx、Ny和Nz段，网格间距分别为Δx(i)(i=1,2,…,Nx)、Δy(j)(j=1,2,…,Ny)和Δz(k)(k=1,2,…,Nz)。经推导，每个六面体单元的内部电场分量可用六面体的12条棱边的场值分量(图2b)通过插值求取：

(5)

式中,上标e表示第e个网格单元。

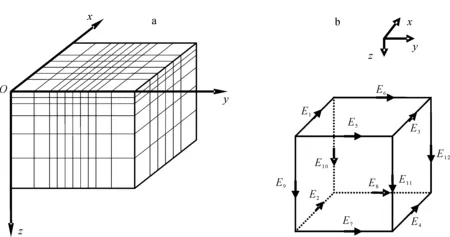
a.区域剖分示意图；b.电场分量位置图。图2 矢量有限元法的区域剖分示意图Fig. 2 Region subdivision schemes of the vector finite element method

将式(5)写成矢量形式：

(6)

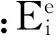
(7)

(8)

(9)

式中：坐标转换函数ζ=(x-xc)/a，η=(y-yc)/b，ζ=(z-zc)/c；(xc,yc,zc)是六面体的中心坐标；2a,2b,2c分别是六面体x,y,z方向的长度；(ζi,ηi,ζi)的取值与棱边编号有关。

由式(3)定义矢量余函数为

(10)

把矢量基函数作为权函数，采用迦辽金方法使整个域内的积分矢量余函数为最小，即

(11)

式中,N为计算域网格单元总数。

将式(10)代入到式(11)，对于第e个单元，得到

(12)

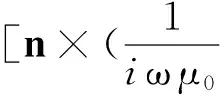
(13)

其中：se表示场源项；Ee表示棱边上的电场；Ke是单元刚度矩阵。Ke是一个12×12阶的复数矩阵，可按下式[19]解析计算得出

(14)

将每个单元电场满足的线性方程进行组合，可以得到整个计算域上电场满足的线性方程组：

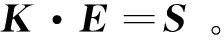
(15)

其中：K是系统刚度矩阵；S是源向量，由计算域的上、下、左、右的边界场值与边界上的单元刚度矩阵计算得到。

采用BICGSTAB方法[20]结合对角块矩阵的不完全LU分解技术求解大型稀疏对称方程(15)，就可以得到计算域上网格单元棱边上的电场值，然后根据麦克斯韦方程组(1a)微分求取磁场。

1.3 视电阻率及阻抗相位计算

根据Newman等[21]的研究，假设两种线性无关的场源激发的表面电场和磁场分别为Ex1，Ey1，Hx1，Hy1，Ex2，Ey2，Hx2，Hy1，可以计算三维MT的张量阻抗：

(16)

张量阻抗的每一个分量可表示成：

(17a)

(17b)

(17c)

(17d)

式(17b)和(17c)定义的响应分别称为xy和yx模式响应，按照下面公式可以求出三维介质的视电阻率和相位：

(18)

其中：i=x,y；j=x,y。

2 三维地形影响模拟与分析

2.1 模型与地形剖分

本项研究基于矩形六面体剖分，矩形网格x，y和z方向的间距可以是不均匀的。地形剖分也采用矩形六面体，比如三维山峰地形的剖分(图3)。

2.2 算法正确性检验

为了验证算法对MT地形影响数值模拟的效果，采用Wannamaker等[2]的二维山峰模型。模型背景电阻率为100 Ω·m，山峰地形如图4所示。设二维山峰地形的走向为x方向，山峰倾向为y方向，z方向垂直向下为正。为了尽量避免对y方向的三维影响，将山峰地形沿x方向延伸34.3 km，整个模型区域(34 300 m×34 300 m×91 993 m)沿x、y和z方向剖分为43×43×29(其中z方向山峰顶面以上7层为空气层)个网格单元。山峰地形采用9个纵向网格单元的划分，网格间距为50 m。

采用本文算法对上述模型进行三维正演模拟，计算频率f=2 Hz时TE极化模式和TM极化模式的视电阻率曲线图(图5)。从图5中可以看出，本文算法(三维矢量有限元)计算的结果与二维有限元的计算结果基本一致，说明本文算法的计算结果准确可靠。

2.3 三维地形影响

为了研究三维地形对MT响应的影响，分别对1个三维山峰地形和1个山谷地形模型进行模拟计算，并与相应的二维地形模拟结果进行比较。

2.3.1 山峰地形

在图4的基础上，将二维山峰地形扩展为三维山峰地形，三维地形在yOz和xOz剖面上的地形图如图6所示。

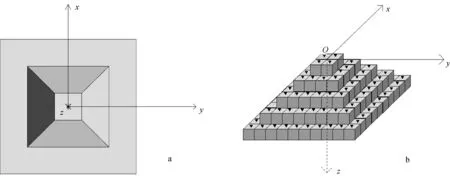
x、y轴向外为正方向。图3 三维地形(a)及地形网格剖分和MT测点(b)示意图Fig. 3 Diagram of 3D terrain(a) and topography grid subdivision and measuring points on MT(b)

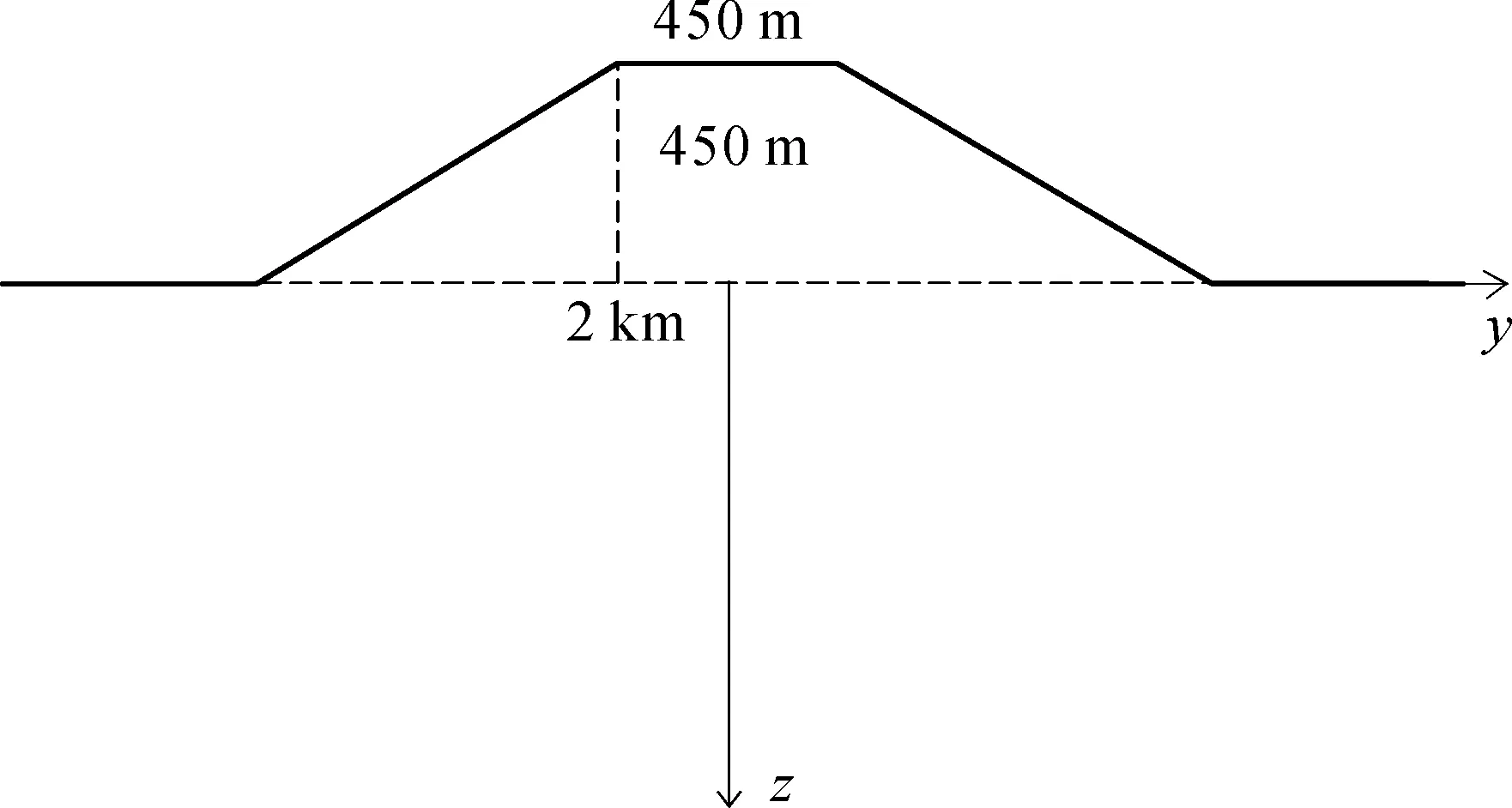
图4 二维山峰地形示意图Fig. 4 Diagram of 2D ridge

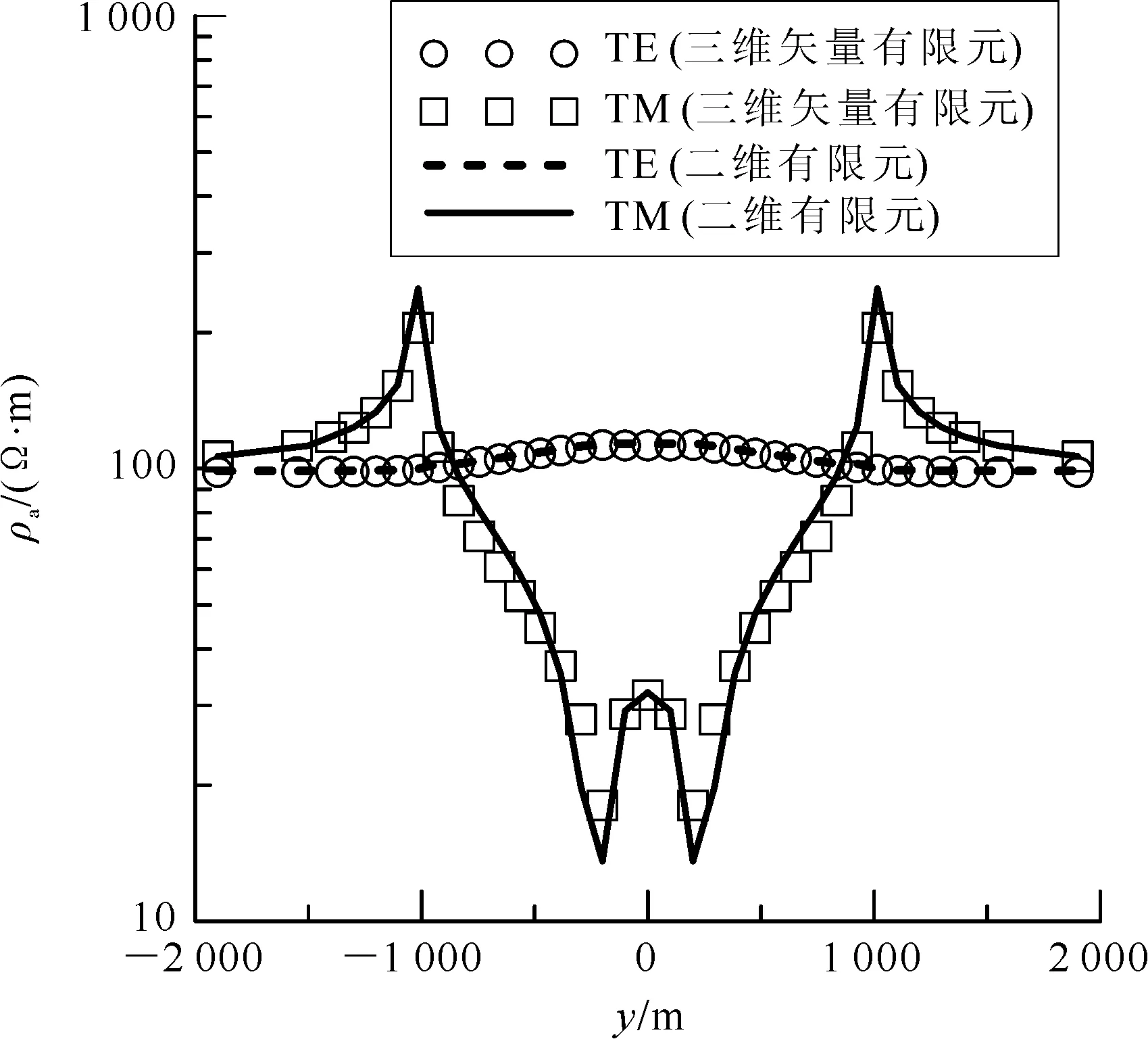
图5 本文算法计算的二维地形影响与二维有限元结果对比图Fig. 5 Comparision between modeling results of 3D VFEM and 2D FEM for 2D ridge

图6 三维山峰地形的yOz(a)和xOz(b)剖面图Fig. 6 Profiles of yOz (a) and xOz (b) of 3D positive trapezoidal-hill

整个模型区域沿x、y和z方向剖分为43×43×29(其中z方向山峰顶面以上7层为空气层)个网格单元。采用本文算法对该模型进行三维正演模拟，模拟结果见图7。从图7可以看出：对于Zxy模式，在山峰左右两边根部的ρaxy高于背景电阻率值，而在山峰上面，ρaxy明显低于背景电阻率值；对于Zyx模式，如果将ρayx平面图旋转90°，其响应规律与ρaxy相同。

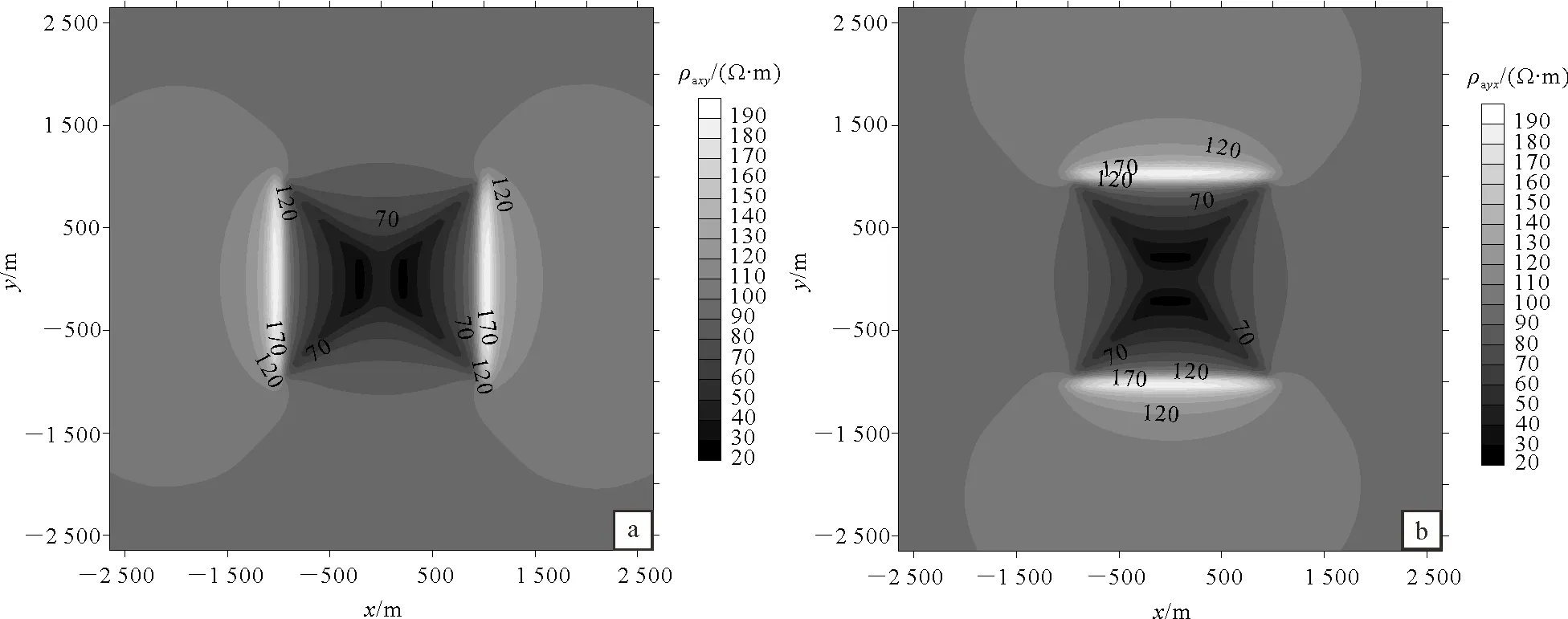
图7 频率为2 Hz山峰模型Zxy模式(a)和Zyx模式(b)的正演视电阻率平面图Fig. 7 Apparent resistivities in Zxy (a) and Zyx (b) modes at 2 Hz for the positive trapezoidal-hill

为了确定是否可以用二维地形模拟结果去近似三维地形的响应，将沿着y方向(x=0，见图6a)的三维模拟结果与二维模拟结果进行比较，比较结果见图8。从图8a可以看出：在山峰上面，Zyx模式的ρaxy值低于背景电阻率值，在山峰根部，ρaxy值高于背景电阻率值；其ρaxy曲线形态与二维TM模式视电阻率曲线形态基本一致。从图8b可以看出，三维Zxy模式的ρaxy与二维地形TE模式响应完全不同，在山峰上面Zxy模式的ρaxy低于背景电阻率值，而二维TE模式视电阻率高于背景电阻率值。

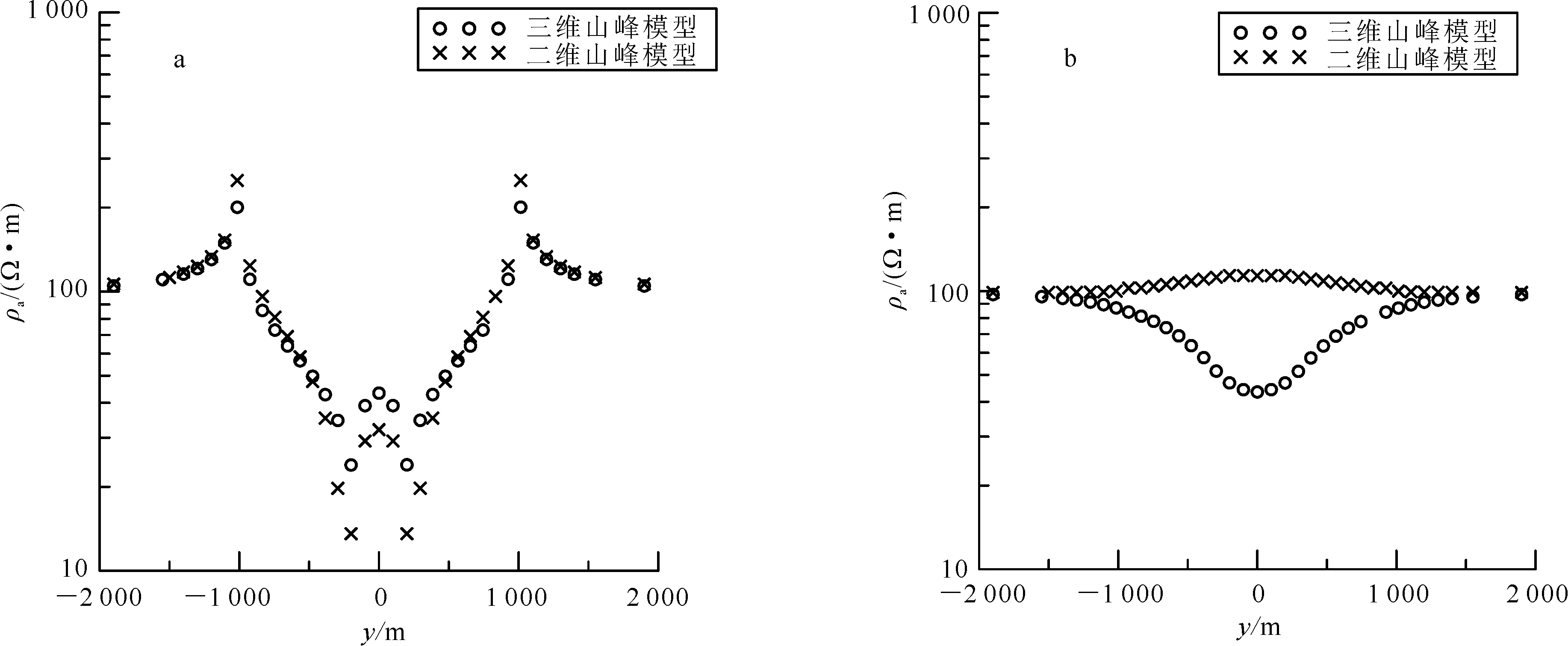
图8 频率为2 Hz山峰地形沿y方向(x=0)的Zyx(a)和Zxy(b)模式与二维TM(a)和TE(b)模式响应视电阻率比较Fig. 8 Apparent resistivities at 2 Hz in Zxy (a) and Zyx (b) modes along line y(x=0) for the positive trapezoidal-hill model,and those in TM (a) and TE (b) modes given by 2D modeling

2.3.2 山谷地形

三维山谷地形如图9所示，其背景电阻率值与三维山峰地形(图6)一样，为100 Ω·m；模型计算区域和网格剖分也与三维山峰模型一致。频率为2 Hz的三维正演模拟结果如图10所示，从图10可以看出，山谷模型正好与山峰模型正演视电阻平面图形态相反：对于Zxy模式，在山谷左右两边顶部的ρaxy低于背景电阻率值，而在山谷底部正上方，ρaxy明显高于背景电阻率值；对于Zyx模式，如果将ρayx平面图旋转90°，其响应规律与ρaxy相同。

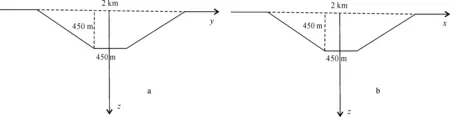
图9 三维山谷地形的yOz(a)和xOz(b)剖面图Fig.9 Profiles of yOz (a) and xOz (b) of 3D negative trapezoidal-hill

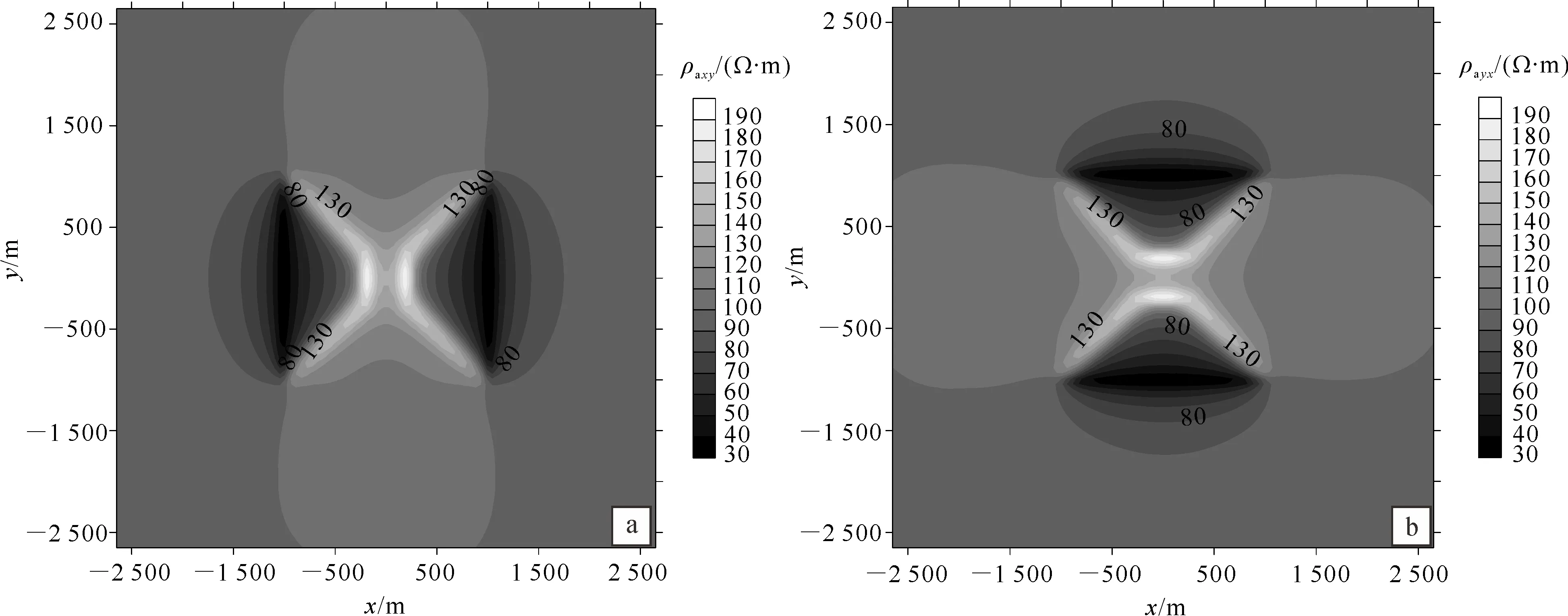
图10 频率为2 Hz山谷模型Zxy模式(a)和Zyx模式(b)的正演视电阻率平面图Fig.10 Apparent resistivities in Zxy (a) and Zyx (b) modes at 2 Hz for the negative trapezoidal-hill

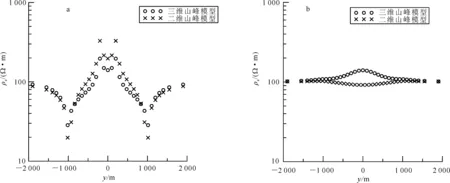
图11 频率为2 Hz山谷地形沿y方向(x=0)的Zyx(a)和Zxy(b)模式与二维TM(a)和TE(b)模式响应视电阻率比较Fig.11 Apparent resistivities at 2 Hz in Zxy (a) and Zyx (b) modes along line y(x=0) for the negative trapezoidal-hill model,and those in TM (a) and TE (b) modes given by 2D modeling

同样，为确定是否可用二维地形影响近似三维地形影响，将沿y方向(x=0，图9a)的三维模拟结果与二维模拟结果进行比较，比较结果见图11。从图11a可以看出，在山谷底部上面，Zyx模式的ρaxy值高于背景电阻率值，在山谷两边的顶部，ρaxy值低于背景电阻率值，其ρaxy曲线形态与二维TM模式视电阻率曲线形态基本一致。从图11b可以看出，三维Zxy模式的ρaxy值与二维地形TE模式响应完全不同，在山谷底部上面Zxy模式的ρaxy高于背景电阻率值，而二维TE模式视电阻率低于背景电阻率值。

3 结论

1)对山脊地形三维正演模拟结果与二维算法模拟结果的比较表明，本文的三维矢量有限元正演计算程序可靠、准确，能够有效地进行大地电磁场的三维地形影响模拟。2)对三维山峰地形和山谷地形的数值模拟表明，MT三维阻抗张量的Zxy模式和Zyx模式都受到地形的影响。3)通过三维山峰地形和山谷地形的三维数值模拟结果与相应二维地形的二维模拟结果比较发现，如果用二维地形模拟结果去近似三维地形响应，二维TE模式与真实三维Zxy模式响应结果差别很大，TM模式接近真实三维Zyx模式响应结果。由模拟结果的比较可得到启示，如果采用二维反演处理带地形三维MT数据，在二维反演剖面展布方向确定的情况下，采用TM极化模式反演更为合理。

[1] Chouteau M, Bouchard K. Two-Dimensional Terrain Correction in Magnetotelluric Surveys[J]. Geophysics, 1988, 53(6): 854-862.

[2] Wannamaker P E,Stodt J A,Rijo L.Two-Dimensional Topographic Responses in Magnetotelluric Model Using Finite Elements[J]. Geophysics,1986, 51(11): 2131-2144.

[3] 赵广茂，李桐林，王大勇，等. 基于二次场二维起伏地形MT有限元数值模拟[J]. 吉林大学学报：地球科学版，2008，38(6)：1055-1059. Zhao Guangmao, Li Tonglin, Wang Dayong, et al. Secondary Field-Based Two-Dimensional Topographic Numerical Simulation in Magnetotellurics by Finite Element Method[J]. Journal of Jilin University: Earth Science Edition, 2008, 38(6): 1055-1059.

[4] 徐世浙，阮百尧，周辉. 大地电磁场三维地形影响的数值模拟[J].中国科学：D辑，1997，27(1): 15-20. Xu Shizhe, Ruan Baiyao, Zhou Hui. Numerical Modeling of 3-D Terrain Effect on MT Field[J]. Science in China: Series D, 1997,27(1): 15-20.

[5] 阮百尧，徐世浙，徐志锋. 三维地形大地电磁场的边界元模拟方法[J]. 地球科学:中国地质大学学报，2007，32(1): 130-134. Ruan Baiyao, Xu Shizhe, Xu Zhifeng. Modeling the 3D Terrain Effect on MT by the Boundary Element Method[J]. Earth Science:Journal of China University of Geosciences, 2007, 32(1): 130-134.

[6] Chen Pofang, Hou Zuozhong, Fan Guohua. Three-Dimensional Topographic Responses in MT Using Finite Difference Method[J]. Acta Seismologica Sinica: English Edition, 1998, 11(5): 631-635.

[7] Baba K,Seama N.A New Technique for the Incor-poration of Seafloor Topography in Electromagnetic Modelling[J]. Geophys J In,2002, 150(2): 392-402.

[8] Mackie R L, Smith J T, Madden T R. Three-Dimensional Electromagnetic Modeling Using Finite Difference Equation: The Magnetotelluric Example[J]. Radio Science, 1994, 29(4): 923-935.

[9] Sasaki Y.3-D Electromagnetic Modelling and Inver-sion Incorporating Topography[C]//ASEG Extended Abstracts. Alderley: Australian Society of Exploration Geophysicists, 2003: 1-7.

[10] Yoshimura R,Oshiman N.Edge-Based Finite Element Approach to the Simulation of Geoelectromagnetic Induction in 3-D Sphere[J]. Geophysics Research Letters, 2002, 29(3): 1039-1042.

[11] Mitsuhata Y,Uchida T.3D Magnetotelluric Modeling Using the T-Ω Finite-Element Method[J]. Geophysics, 2004, 69(1): 108-119.

[12] Shi X, Utada H, Wang J, et al. Three Dimensional Magnetotelluric Forward Modeling Using Vector Finite Element Method Combined with Divergence Corrections(VFE++)[C]//17th IAGA WG 1.2 Workshop on Electromagnetic Induction in the Earth. Hyderabad: [s.n.], 2004:465-473.

[13] Nyung Jin Nam, Hee Joon Kim, Yoonho Song, et al. 3D Magnetotelluric Modelling Including Surface Topography[J]. Geophysical Prospecting, 2007, 55(2): 277-287.

[14] Liu C, Ren Z, Tang J, et al. Three-Dimensional Magnetotellurics Modeling Using Edge-Based Finite-Element Unstructured Meshes[J]. Applied Geophysics, 2008, 5(3): 170-180.

[15] 刘长生，汤井田，任政勇，等. 基于非结构化网格的三维大地电磁自适应矢量有限元法模拟[J]. 中南大学学报：自然科学版，2010，41(5)：1855-1859. Liu Changsheng, Tang Jingtian, Ren Zhengyong, et al. Three-Dimension Magnetotellurics Modeling by Adaptive Edge Finite-Element Using Unstructured Meshes[J]. Journal of Central South University: Science and Technology, 2010, 41(5): 1855-1859.

[16] Mackie R L, Madden T R, Wannamaker P E. Three-Dimensional Mangnetotelluric Modeling Using Difference Equations-Theory and Comparisons to Integral Equation Solutions[J]. Geophysics, 1993, 58(2): 215-226.

[17] Siripunvaraporn W, Egbert G, Lenbury Y. Nu-merical Accuracy of Magnetotelluric Modeling: A Comparison of Finite Difference Approximations[J]. Earth Planets Space, 2002, 54(6): 721-725.

[18] 汤井田，薛帅. MT有限元模拟中截断边界的影响[J]. 吉林大学学报：地球科学版，2013，43(1)：267-274. Tang Jingtian, Xue Shuai. Influence of Truncated Boundary in FEM Numerical Simulation of MT[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(1): 267-274.

[19] 金建铭. 电磁场有限元方法[M]. 西安：西安电子科技大学出版社，1998：179-189. Jin Jianming. The Finite Element Method in Electromagnetic Fields[M]. Xi’an: XiDian University Press, 1998: 179-189.

[20] Sadd Y. Iterative Methods for Sparse Linear Systems[M]. 2nd ed. Philadelphia: Society of Industrial and Applied Mathematics, 2003: 228-234.

[21] Newman G A, Alumbaugh D L. Three-Dimensional Magnetotelluric Inversion Using Non-Linear Conjugate Gradients[J]. Geophys J Int, 2000, 140(2): 410-424.

华北地台、华北克拉通、华北板块、华北古陆、华北地块等名词的用法

邱殿明，蒋 函，刘雅琴

吉林大学学报(地球科学版)编辑部，长春 130026

地学科技期刊中华北地台、华北克拉通、华北板块、华北古陆、华北地块等词汇比较常见，但使用比较混乱，有必要梳理这几个名词的定义及用法，以便在这些词汇使用上有一个统一性。

槽台学说基于地壳活动和稳定性的差别，将地壳的一级构造单元划分为地槽(褶皱系)和地台；板块构造说认为地球表层是由为数不多的大小不等的岩石圈板块拼合起来的，将六大板块作为全球的一级构造单元，并将分隔它们的边界也作为构造带看待。 华北地台、华北板块词汇分别是上述2种学说中的一级单元内部进一步划分出的次一级，乃至更小的构造单元，分属于2种学说的专有名词;而其他词汇均为构造地质学上的普通专业名词。

地台(platform)又称为陆台，指地壳上稳定的、形成后未再遭受褶皱变形的地区。地台具有双层结构：上部为未经变形、大体保持水平产状的浅海相或陆相沉积盖层；下部是已经强烈变形和变质的前寒武纪结晶基底。华北地台(North China platform)挟持于阴山-燕山与秦岭--大别两条造山带之间，范围包括华北、东北南部、渤海湾等地。因它包括朝鲜半岛，黄汲清(1945)又称之为中朝地台；鉴于它的面积较世界上其他地台小得多，且活动性较大，又称为中朝准地台。有些学者又称为中朝克拉通(Sino-Korea craton)[1]。

克拉通(craton)是地壳形成之后(至少自显生宙以来)保持稳定状态、极少经受强烈构造变形的构造单元。现今的克拉通指大陆克拉通[1]。华北(中朝)克拉通范围同华北地台。

板块(plate)是地球岩石圈被洋中脊、岛弧海沟系、转换断层等三大构造活动带分割形成的大小不一的连续的岩石圈块体。全球由欧亚板块、太平洋板块、印度洋板块、非洲板块、美洲板块和南极洲板块等六大板块组成[1]。华北(中朝)(North China plate)板块属于中板块，其范围包括了华北地台及其边缘造山带。

古陆(oldland)泛指地史时期中各种形式的古老剥蚀陆地，未严格区分其规模大小、海拔高度、地貌形态和延续时间。华北(中朝)古陆(North China oldland)包括华北地区大部、内蒙古南部、东北南部及整个朝鲜半岛范围，在大地构造单元上属于中朝地台范围，地质历史中也具有大体相似的古地理面貌[1]。当华北地台在地史某个时期中呈剥蚀陆地状态时，称为华北古陆。一般描述古地理的时候称华北古陆。

地块(land mass)是具有一定综合结构形态，属于一定构造体系的地质块体[1]。华北地块(North China block)原属古中国地块的一部分，是一个具有古老构造基底的地台。其范围同原华北地台，主体位于阴山以南和秦岭、大别山系以北广大地区之间。震旦纪至三叠纪，经历了漫长的相对稳定时期，主要表现为地块整体升降，地层岩相稳定，厚度变化不大，岩浆活动不发育。中、新生代构造活动活跃，受断裂控制，逐渐解体为规模不等的断块。黄汲清(1945)认为李希霍芬等命名的“震旦地块”，不仅包含华北并且还包含朝鲜的大部，因而应改称为中朝地块(Sino-Korea massif)。它包括内蒙地轴、东满地块、南朝鲜地块、山东地块及淮阳地盾、秦岭地轴、鄂尔多斯地台等次一级的构造单元。1980年黄汲清等在进一步综合大量的基本资料后，改称为中朝准地台[2]。可见，华北地块和中朝地块及中朝准地台基本一致，建议尽量使用中朝准地台，而不要使用中朝地块。

论文描述的时候，如果采用板块构造学说，那么就应称为华北板块；若采用槽台学说就称为华北地台(中朝地台、中朝准地台)。至于华北克拉通，可以分别与华北板块和华北地台一起使用，但华北板块和华北地台不能一起使用。而华北古陆使用时应当慎重，华北地台只是某个时期处于剥蚀状态时才能称之为华北古陆。华北地块是一个泛词，可用于各个学说里。

参考文献：

[1] 《地球科学大辞典》编委会.地球科学大辞典：基础学科卷[M]. 北京：地质出版社，2006.

[2] 地质矿产部地质辞典办公室.地质辞典：一：普通地质构造地质分册下册[M].北京：地质出版社，1983.

Modeling for the Effect of Magnetotelluric 3D Topography Based on the Vector Finite-Element Method

Gu Guanwen1, 2, Wu Wenli2, Li Tonglin1

1.CollegeofGeoExplorationScienceandTechnology,JilinUniversity,Changchun130061,China2.InstituteofGeophysicalandGeochemicalExploration,Langfang065000,Hebei,China

It is of great significance to study the effect of topography to the magnetotelluric inversion and interpretation. A vector finite-element algorithm has been applied to simulate magnetotelluric (MT) effect of 3D topography models. First, the algorithm was verified by comparison with the modeling result of a 2D ridge model. Then, the effect of 3D topography was simulated for a 3D positive trapezoidal-hill model and a negative trapezoidal-hill model respectively. In addition, we also compared the results of 2D and 3D simulation. The results show thatZxyandZyxare both affected by the terrain, the difference between 2D TE mode and real 3D response is great, whereas the 2D TM mode response is similar to the real 3D response. If we invert the 3D MT data by a 2D program with terrain, the TM polarization mode inversion is more reasonable.

magnetotelluric; 3D terrain; numerical modeling; vector-finite-element

10.13278/j.cnki.jjuese.201405302.

2014-02-01

国家重大科学仪器设备开发专项项目(2011YQ05006006);中国地质调查局项目(1212011220247)

顾观文(1975--)，男，博士研究生，高级工程师，主要从事电磁法正、反演研究及其软件研制工作，E-mail:guguanwen@igge.cn

李桐林(1962--)，男，教授,博士生导师，主要从事电磁法理论及应用研究，E-mail:litl@jlu.edu.cn。

10.13278/j.cnki.jjuese.201405302

P631.3

A

顾观文，吴文鹂，李桐林. 大地电磁场三维地形影响的矢量有限元数值模拟.吉林大学学报:地球科学版,2014,44(5):1678-1686.

Gu Guanwen, Wu Wenli, Li Tonglin. Modeling for the Effect of Magnetotelluric 3D Topography Based on the Vector Finite-Element Method.Journal of Jilin University:Earth Science Edition,2014,44(5):1678-1686.doi:10.13278/j.cnki.jjuese.201405302.