基于多元线性回归的HTEM三维异常体电导率－深度识别

嵇艳鞠，冯 雪，于明媚，徐 江，呼彦朴，关珊珊

吉林大学仪器科学与电气工程学院/地球信息探测仪器教育部重点实验室，长春 130026

0 引言

时域航空电磁法（helicopter－borne timedomain electromagnetic method，HTEM）被成功应用于金属矿勘查、地质填图、水文地质调查和环境监测等领域［1－3］。该方法具有快速、经济、勘探深度大、解释精度高、分辨率高等优点，是矿产资源勘查的有效方法之一，尤其适用于我国老矿区周边寻找新矿以及深部找矿［4］。

目前，时域航空电磁数据处理主要集中在电导率深度转换、电导率深度成像方面。王绪本等［5－6］计算了视电阻率以及一维反演、二维近似反演方面的研究。强建科等［7］进行了时域航空全区视电阻率计算研究。朱凯光等［8］研究了神经网络、主成分分析等电导率－深度成像方法，并取得了良好效果。

在航空电磁飞行测量时，每个飞行架次测量的数据量在几万兆字节以上，数据量很大，进行电导率深度成像（conductivity depth imaging，CDI）需要花费大量时间。因此，学者们开始研究航空电磁数据的快速解释和异常识别方法。Liu［9］基于水平薄板，将电阻率－深度图像用于航空瞬变电磁数据处理中。Smith等［10］研究球体模型的电导率离散方法，进而推断导体的深度。Claprood等［11］采用加权多元线性回归方法，基于薄板模型对电磁异常进行了检测和精细识别，并在加拿大地区薄板类VMS（volcanogenic massive sulphides）矿床进行了验证，并取得了较好的效果。

目前计算时域三维异常体的电磁响应已实现，为开展三维异常体的快速识别奠定了基础。笔者基于航空瞬变电磁理论，用三维异常体模型近似表示地下复杂的矿体分布，计算不同电导率、深度的异常体响应值，提取属性后，应用社会科学统计软件包（statistical product and service solutions，SPSS）进行回归分析［12］。建立异常体电导率、深度与属性之间的回归方程，进而实现异常体的电导率和深度快速计算。

1 三维模型样本建立及属性提取

笔者基于三维有限差分数值计算方法［13－15］，结合吉林大学研制的直升机时域电磁测量系统参数［16］，计算了多组直立三维异常体的三分量感应电动势Vx（t）、Vy（t）、Vz（t）（t为取样时间），构建了三维异常体模型电磁响应样本库。时域航空电磁系统工作参数如表1所示。三维异常体模型计算参数如表2所示。

表1 航空电磁系统工作参数Table 1 Operating parameters of airborne electromagnetic system

表2 航空三维异常体模型计算参数Table 2 Calculation parameters of airborne three－dimensional anomalies model

对上述感应电动势Vx（t）、Vy（t）、Vz（t）进行取样，t为0.2～1.5ms，得到一系列反应三维异常体电磁响应与位置关系的剖面曲线。剖面曲线形态基本包含以下几种情况：单峰异常、双峰异常和多峰异常，如图1所示。

为提取表示三维异常体特征的电磁属性，以判断地下异常体的形状、长度和时间独立性，我们定义了如下参数：Vx1（t）为x方向感应电动势的较大峰值，Sx1为Vx1（t）所对应的横坐标，即异常体相对于原点的水平位移；Vx2（t）为x方向感应电动势的较小峰值，Sx2为Vx2（t）所对应的横坐标。同上，Vz1（t），Sz1，Vz2（t），Sz2为相应的z方向的参数。V1为较大峰值所对应的总感应电动势，V2为较小峰值所对应的总感应电动势。总感应电动势公式表示为

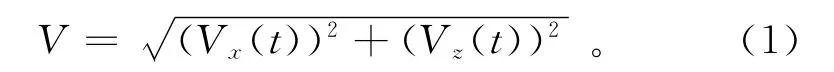
电磁属性的定义如表3所示。按航空三维异常体模型的计算参数，将相应计算得到的感应电动势和7个电磁属性整理到一起，即得到三维异常体模型的样本库。

2 多元线性回归方程建立

在建立航空三维异常体模型样本库，提取电磁响应属性的基础上，建立流程图如图2所示的回归方程。

表3 电磁属性定义Table 3 Definition of meaning of attributes

具体步骤如下。

1）以三维异常体的电导率、深度为因变量，建立电导率、深度参数全回归方程；

2）应用学生化剔除残差和库克距离2个参量对样本数据进行离群值诊断，一旦出现离群值，将该组数据剔除，重新建立全回归方程，再进行离群值诊断，直到样本数据中不存在离群值为止；

3）从方差扩大因子、特征值、条件索引、方差比例4个方面进行多重共线性诊断，如果存在多重共线性，采用逐步回归方法剔除一些不重要的自变量，进行参数优化；

图1 剖面曲线的属性参数描述Fig.1 Attribute parameters of profile curve

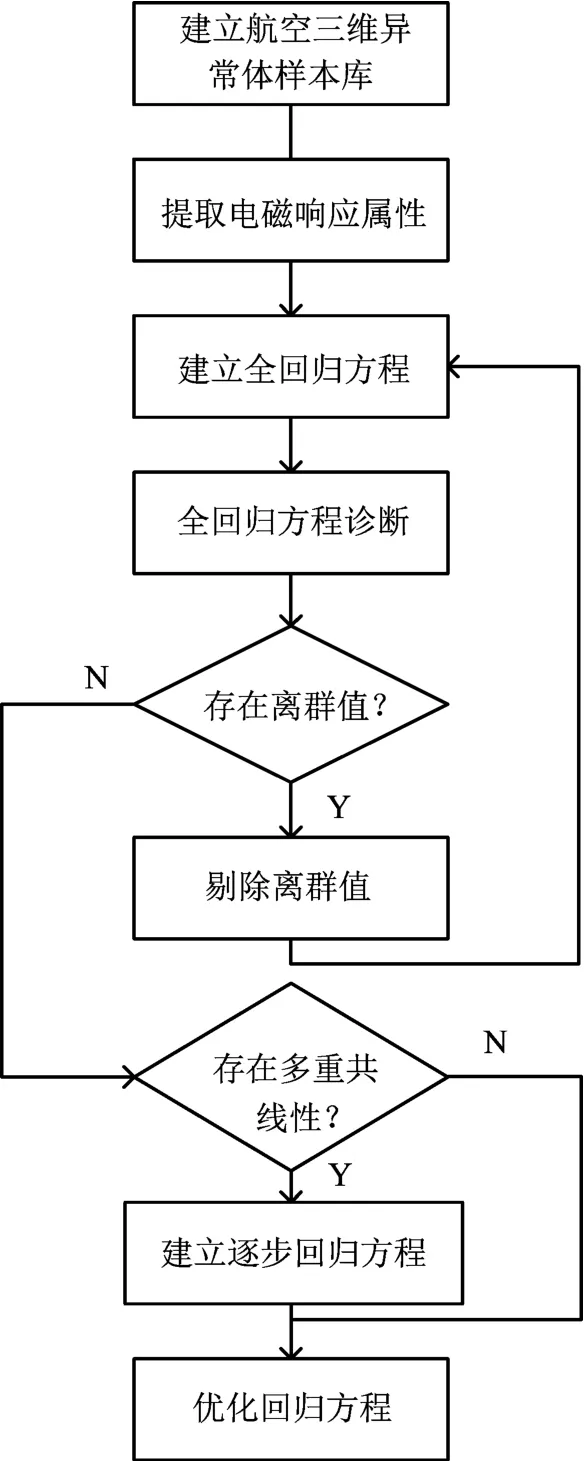
图2 回归方程建立流程图Fig.2 Flow chart of building regression equation

4）最后采用逐步回归法，建立电导率、深度参数的最优回归方程。

2.1 电导率参数回归方程

2.1.1 全回归方程的建立

采用已有样本库中的722组数据，将异常体电导率作为回归方程的因变量，本文定义的7个属性作为自变量，把自变量全部引入到回归方程中，建立全回归方程。基于 OLSE（ordinary least square estimation），建立电导率的全回归方程，表达式为

式中：α1—α7前面的系数为标准回归系数，即消除了因变量与自变量所取单位影响的回归系数。标准回归系数的绝对值大小直接反映了它所对应的自变量对因变量的影响程度。

初步建立回归方程后，根据回归诊断理论，对回归方程的合理性、准确性和可靠性进行检查，进而不断地改善和提高回归分析的质量［16］，得到最优的回归方程。

2.1.2 方程的诊断

回归方程一旦出现离群值或者多重共线性问题，将导致方程精度降低或使方程不稳定。

1）离群值诊断

离群值主要指回归方程中的异常值［17］，它的存在将导致统计分析误差增大、测量精度降低。笔者通过学生化剔除残差对全回归方程（2）的因变量进行离群值诊断，采用库克距离对自变量数据进行离群值诊断［18］。

首先进行因变量的离群值诊断。第i个观测值的学生化剔除残差eSDRi的表达式为

式中：eSDRi为第i个观测值的学生化残差；n为样本数据数；p为自变量数。在利用学生剔除化残差诊断异常值时，一般认为｜eSDRi｜＞3的相应观测值为异常值［19］；而全回归方程（2）｜eSDRi｜的极大值为2.306，故因变量的样本数据中无离群值。

而后进行自变量的离群值诊断。需要先判断样本数据中的强影响点。hii为H（因变量的帽子矩阵）主对角线的第i个元素，也称为杠杆值，将杠杆值中心化为

其平均值为

当或时，样本点为强影响点，本文取前者。若某一点被判断为强影响点，需要进一步计算该样本点对应的库克距离来判断该离群值是否由自变量的原因导致。

第i个观测值对应的库克距离Di的表达式为

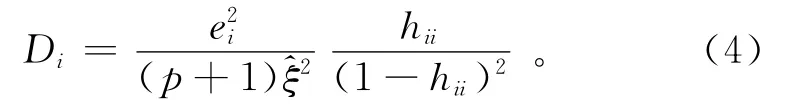
式中：ei为残差为误差项的方差。

若所测样本数据的库克距离极大值大于1，则认为存在由自变量的原因产生的离群值［19］。电导率回归方程（2）的库克距离极大值为3.165，故判断自变量存在离群值。

基于以上诊断剔除因变量和自变量的离群值，重新建立回归方程：

回归方程（5）的复相关系数R＝0.784，统计量F＝162.722。当分子自由度为7、分母自由度为712时，查表得显著性水平取0.05所对应的F值为F0.05＝2.022 4。由于F＞F0.05，故离群值诊断后所建立的方程显著。

2）共线性诊断

如果建立的回归方程存在多重共线性，回归参数估计量的抽样误差就会偏大；同时，回归参数值和符号都会不稳定。这些问题会使建立的回归方程失去实际意义，因此要对全回归方程（2）进行共线性诊断。

一种是利用方差扩大因子法进行诊断。若某个自变量对应的方差扩大因子VIF（variance inflation factor）≥10，则此自变量与其余自变量之间有严重的多重共线性，需要对此自变量进行处理。经计算，文中定义的7个自变量中，只有α3对应的VIF3＝37.032≥10和α4对应的VIF4＝43.452≥10，所以α3、α4与其余自变量之间存在多重共线性。

另一种是利用特征根判定法进行共线性诊断，表4给出了在维数逐渐增加时对全回归方程（2）诊断结果。X是多元线性回归中的设计矩阵，维数是指观测样本的组数。当维数为8时，X′X的特征根为0。根据矩阵行列式的性质可知，若｜X′X｜＝0，则由特征根判定法推断该方程存在多重共线性［19］。另外，若存在条件数k≥10，说明各自变量间存在多重共线性。由SPSS软件计算，计算结果最大的条件数k8＝129.77，由此也可推断方程存在较强的多重共线性。

2.1.3 逐步回归方程

为了消除多重共线性的影响，笔者采用逐步回归法剔除一些不重要的自变量，建立逐步回归方程［20］。

在逐步回归中，引进变量和剔除变量的显著性水平是不同的，进入方程的显著性水平取0.05，出方程的显著性水平取0.10，不符合这些指标的自变量会被SPSS软件自动剔除。表5给出了自变量逐步引入的过程。一般认为：R2越大，且越接近于1.000，则回归方程显著性越高，效果越理想；SSE（残差平方和）越小，则方程建立的效果越好。表5显示的是按标准回归系数的大小引入自变量的过程，其结果说明，随着自变量的引入，回归方程的效果逐渐变好。

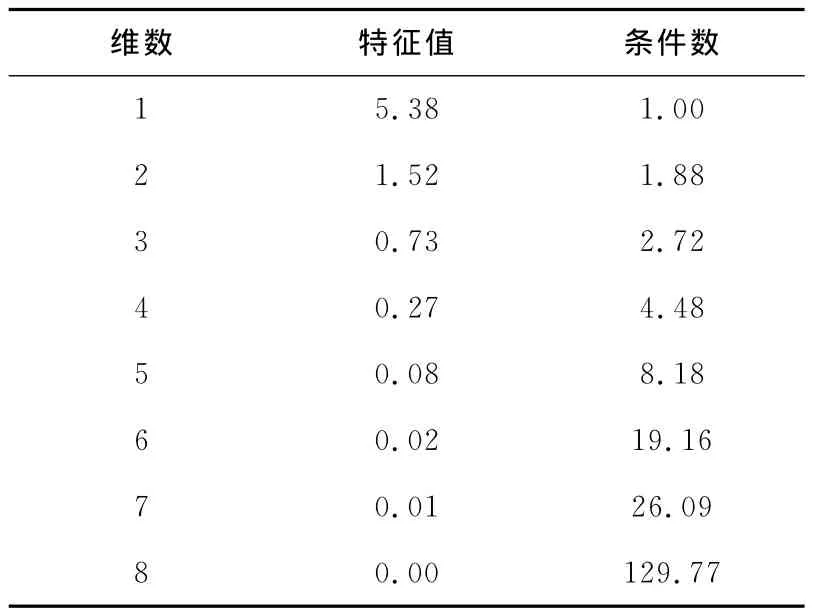
表4 全回归方程共线性诊断结果Table 4 Results of multicollinearity diagnosis of the full regression equation

表5 逐步方程的引元过程Table 5 Process of importing the independent variables in the stepwise regression

最后，建立电导率的逐步回归方程表达式为

在回归方程表达式（8）中：经计算验证，自变量α1，α5，α6的方差扩大因子均小于10，说明该方程中不存在多重共线性；F统计量显著性为0，故自变量整体对因变量高度显著；t分布双尾显著性概率皆小于0.05，故标准回归系数都显著。另外由（8）可知，自变量α5的标准回归系数的绝对值最大，因此α5对因变量的影响最大。

2.2 深度参数回归方程

由表2提供的参数，笔者共计算得到209组不同深度的样本模型。根据与电导率参数回归方程相同的步骤，建立深度参数全回归方程。进行离群值和共线性诊断后，建立异常体深度的逐步回归方程，其表达式为

3 回归方程正确性分析

根据时域电磁场理论，三维异常体的电导率直接决定了电场和磁场衰减曲线的规律［21］，以及剖面曲线的半峰值宽度，而衰减曲线和剖面曲线的这些性质直接影响了α5、α1、α6的值。由此可见，电导率与α5、α1、α6是互相制约、互相影响的，这从理论上说明在以电导率为因变量的回归方程引入自变量α5、α1、α6是正确的。与此同时，将本文的回归方程与Maxime Claprood［11］建立电导率的逐步回归方程进行对比，引入的自变量相同，与本文结论一致。

电磁波传播的趋肤深度与异常体的电导率、电磁响应的衰减快慢有直接关系，这些性质与电磁属性α4，α5相关。因此，深度参数的回归方程引入自变量α4，α5是合理的；并且这与Palacky等［22］的结论一致。

表6给出了电导率和深度逐步回归方程的调整R2和SSE值。可以看出，深度参数的调整R2接近于1.000，其逐步回归方程高度显著，说明深度回归方程有效。在建立电导率方程时，采用的样本数据量较小，三维正演模型电导率的取值偏离正态分布较大，导致其调整R2较小。尽管如此，由于建立电导率方程的SSE值较小，这说明电导率回归方程依然有效。

表6 逐步回归方程参数Table 6 Parameter of regression equation

4 模型精度和校验精度

模型精度显示回归方程对建立此方程的样本数据的适应情况；校验精度显示回归方程对样本以外数据的适应情况。笔者利用相对误差来检验模型精度和校验精度。假设三维异常体模型的实际参数为ψ0，其估计值为，该参数相对误差为

采用用来建立回归方程的722组电导率数据、209组深度数据样本进行回归方程的模型精度测试。当取样时间t为0.2～1.5ms时，电导率模型的相对误差为1.14%～11.95%，深度模型的相对误差为0.36%～13.19%。

由于现有数据的限制，笔者选取6组非检测模型精度的数据模型（图3）对回归方程进行校验精度分析。6组模型的布线方式均为中心回线方式，异常体尺寸均为60m×60m×60m，围岩电导率均为0.01S/m，异常体电导率和深度如表7所示。计算结果为：当t为0.20～0.37ms时，电导率校验的相对误差为0%～19.07%；当t为0.46～0.87ms时，深度校验的相对误差为0.39%～11.15%。此结果说明电导率、深度回归方程对一个异常体的模型识别较准确，适用性较好。

图3 校验模型一Fig.3 Calibration mode one

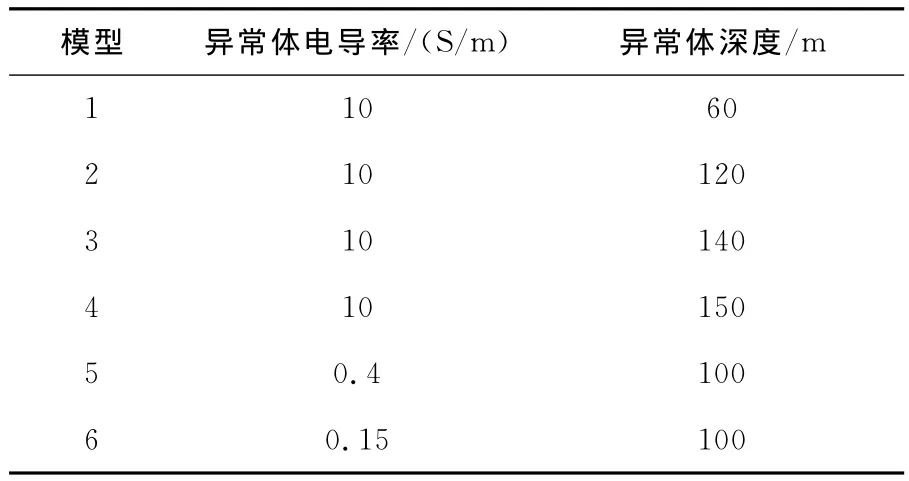
表7 航空三维异常体校验模型电导率及深度Table 7 Conductivity and depth of airborne three－dimensional anomalies calibration model

为了进一步探究回归方程（8）和（9）的适用性，笔者计算了同时存在两个异常体的模型。异常体1的尺寸为60m×60m×60m，异常体2的尺寸为30m×30m×30m，其他参数如图4所示。计算模型的感应电动势值，并提取属性后，将相应属性带入电导率逐步回归方程（8）和深度逐步回归方程（9）。当t为0.2～0.5ms时：取40m为ψ0进行对深度的精度校验，相对误差为2.76%～40.47%；取10S/m为ψ0进行电导率精度校验，相对误差为2.46%～29.13%；取0.1S/m为ψ0进行电导率精度校验，相对误差均大于100%。由此可知，两个异常体的总电导率效果趋近于异常体1单独存在的电导率，此回归方程用于检测两个异常体时精度不高；说明笔者建立的回归方程用于两个异常体的模型识别时结果不准确，适用性较差。

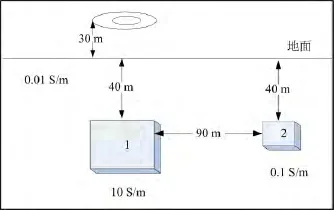
图4 校验模型二Fig.4 Calibration mode two

5 结语

时域航空电磁飞行测量数据量大、数据解释困难，笔者在建立三维异常体的电磁响应样本库的基础上，采用多元线性回归法，建立异常体电导率、深度的多元回归方程。笔者通过调整分析回归方程的相关系数和残差平方和，计算模型精度和校验精度，并且建立电导率回归方程和深度回归方程，分别与Maxime Claprood的电导率回归方程和Palacky的深度回归方程进行对比，结果显示引入的自变量相同，与本文结论一致，说明本文采用逐步回归法建立三维异常体电导率和深度方程是完全可行的，是一种有效、准确、快速的识别方法。

笔者在建立电导率、深度回归方程时，采用的模型数据量相对来说较少，电导率取值分布不成正态分布，这导致当样本数据发生改变时，回归方程不稳定。当地下有两个异常体时，回归方程的识别效果不太理想。只有当模型数量足够多，充分考虑异常体的多样性，才可以提高回归方程的稳定性，进而真正用于野外航空电磁飞行测量时的海量数据异常快速检测和识别。

（Reference）：

［1］Fountain D.60Years of Airborne EM－Focus on the Last Decade［C］//AEM 2008 5th International Conference on Airborne Electromagnetics.Haikko Manor：［s.n.］，2008.

［2］雷栋，胡祥云，张素芳.航空电磁法的发展现状［J］.地质找矿论丛，2006，21（1）：40－53.Lei Dong，Hu Xiangyun，Zhang Sufang.Development Status QUO of Airborne Electromagnetic［J］.Contributions to Geology and Mineral Resources Research，2006，21（1）：40－53.

［3］张昌达.航空时间域电磁法测量系统：回顾与前瞻［J］.工程地球物理学报，2006，3（4）：265－273.Zhang Changda，Airborne Time Domain Electromagnetic System：Look Back and Ahead［J］.Chinese Journal of Engineering Geophysics，2006，3（4）：265－273.

［4］嵇艳鞠，栾卉，李肃义，等.全波形时间域航空电磁探测分辨率［J］.吉林大学学报：地球科学版，2011，41（3）：885－891.Ji Yanju，Luan Hui，Li Suyi，et al.Resolution Study of Full－Waveform Airborne TEM［J］.Journal of Jilin University：Earth Science Edition，2011，41（3）：885－891.

［5］毛立峰，王绪本.航空电磁快速反演技术［C］//中国地球物理·2009.合肥：中国科学技术大学出版社，2009.Mao Lifeng，Wang Xuben.Fast Inversion of Airborne Electromagnetic［C］//The Chinese Geophysics·2009.Hefei：University of Science and Technology of China Press，2009.

［6］郑凯，王绪本，陈斌，等.基于矩阵束法的时域航空电磁响应数据的重构［J］.物探与化探，2010，34（6）：737－749.Zheng Kai，Wang Xuben，Chen Bin，et al.Reconstruction of Time Domain Airborne Electromagnetic Response Data Based on Matrix Pencil Method［J］.Geophysical ＆ Geochemical Exploration，2010，34（6）：737－749.

［7］强建科，罗延钟，汤井田.航空瞬变电磁法的全时域视电阻率计算方法［J］.地球物理学进展，2010，25（5）：1657－1661.Qiang Jianke，Luo Yanzhong，Tang Jingtian.The Algorithm of All－Time Apparent Resistivity for Airborne Transient Electromagnetic（ATEM）Survey［J］.Progress in Geophysics，2010，25（5）：1657－1661.

［8］Zhu Kaiguang，Ma Mingyao，Cheng Hongwei，et al.PC－Based Artificial Neural Network Inversion for Airborne Time－Domain Electromagnetic Data［J］.Applied Geophsics，2012，9（1）：1－8.

［9］Liu G.Conductance－Depth Imaging of Airborne TEM Data［J］.Exploration Geophysics，1993，24：655－662.

［10］Smith R S，Salem A S.A Discrete Conductor Transformation of Airborne Electromagnetic Data［J］.Near Surface Geophysics，2007，5：87－95.

［11］Claprood M，Chouteau M，Cheng L Z.Rapid Detection and Classification of Airbrone Time－Domain Electromagnetic Anomalies Using Weighted Multi－Linear Regression［J］.Exploration Geophysics，2008，39：164－180.

［12］朱建伟，赵刚，刘博，等.油页岩测井识别技术及应用［J］.吉林大学学报：地球科学版，2012，42（2）：289－295.Zhu Jianwei，Zhao Gang，Liu Bo，et al.Identification Technology and Application of Well－Logging About Oil Shale［J］.Journal of Jilin University：Earth Science Edition，2012，42（2）：289－295.

［13］许洋铖，林君，嵇艳鞠，等.航空时间域电磁法回线源有限差分初始场计算［J］.电波科学学报，2010，25（2）：259－264.Xu Yangcheng，Lin Jun，Ji Yanju，et al.Calculation of Initial Field for Loop Source in Airborne Time－Domain Electromagnetic by Finite－Difference Approch［J］.Journal of Radio Science，2010，25（2）：259－264.

［14］闫述，陈明生，傅君眉.瞬变电磁场的直接时域数值分析［J］.地球物理学报，2002，45（2）：275－283.Yan Shu，Chen Mingsheng，Fu Junmei.Direct Time－Domain Numerical Analysis of Transient Electromagetic Fields［J］.Chinese Journal of Geophysics，2002，45（2）：275－283.

［15］许洋铖，林君，李肃义，等.全波形时间域航空电磁响应三维有限差分数值计算［J］.地球物理学报，2012，55（6）：2105－2114.Xu Yangcheng，Lin Jun，Li Shuyi，et al.Calculation of Full－Waveform Airborn Electromagnetic Response with Three－Dimention Finite－Difference Solution in Time－Domain［J］.Chinese Journal of Geophysics，2012，55（6）：2105－2114.

［16］王寅琮.回归分析中异常值与共线性的诊断［D］.秦皇岛：燕山大学，2011.Wang Yincong.Diagnoses About Abnormal Values and Co－Linearity in Regression Analysis［D］.Qinhuangdao：Yanshan University，2011.

［17］王中宇，张海滨，刘智敏.剔除离群值的学生化残差新方法［J］.仪器仪表学报，2006，27（6）：624－637.Wang Zhongyu，Zhang Haibin，Liu Zhimin.The Novel Method for Outliers’Rejection of the Studentized Residual Error［J］.Chinese Journal of Scientific Instrument，2006，27（6）：624－637.

［18］段晨龙，赵跃民，何亚群，等.废弃电路板破碎产物粒度分形分布的研究［J］.中国矿业大学学报，2009，38（3）：357－360.Duan Chenlong，Zhao Yuemin，He Yaqun，et al.Research on the Fractal Model of Size Distribution of Crushed Waste Printed Circuit Boards［J］.Journal of China University of Mining ＆ Technology，2009，38（3）：357－360.

［19］何晓群，刘文卿.应用回归分析［M］.3版.北京：中国人民大学出版社，2011.He Xiaoqun，Liu Wenqing.Applied Regression Analysis［M］.3rd ed.Bejing：China Renmin University Press，2011.

［20］徐金明，刘斌，孙昆仑.岩体边坡中流体包裹体参数的逐步 回 归 分 析［J］.岩 石 学 报，2007，23（9）：2059－2062.Xu Jinming，Liu Bin，Sun Kunlun.Stepwise Regression Analysis to Parameters of Fluid Inclusion Planes in Rock Slopes［J］.Acta Petrologica Sinica，2007，23（9）：2059－2062.

［21］嵇艳鞠.浅层高分辨率瞬变电磁系统中全程二次场提取技术研究［D］.长春：吉林大学，2004.Ji Yanju.All－Time Secondary Electromagnetic Field Extraction in High Resolution Transient Electromagnetic System for Subsurface Imaging［D］.Changchun：Jilin University，2004.

［22］Palacky G，West G.Quantitative Measurements of Input AEM Measurements［J］.Geophsics，1973，38：44－50.