纵横波弹性阻抗联合反演方法

张广智，杜炳毅，陈怀震，高建虎，李 超，李 远

1.中国石油大学（华东）地球科学与技术学院，山东 青岛 266580

2.中国石油勘探开发研究院西北分院，兰州 730020

3.东方地球物理公司新兴物探开发处，河北 涿州 072750

0 引言

为了充分利用实际地震资料非零炮检距的特点，近年来，许多学者对叠前地震反演做了大量的研究工作［1－5］。Connolly［6］根据声阻抗的思想提出了弹性阻抗（elastic impedance）的概念，并且推导了弹性阻抗公式。Larsen［7］利用PP波和PS波叠前地震数据同步反演方法获取了较好的纵波阻抗和横波阻抗的估计值。Milos［8］将弹性阻抗反演应用到实际资料中，充分利用小角度道集和大角度道集资料，提高了反演的可靠性。Duffaut等［9］在Connolly研究的基础上提出横波弹性阻抗的概念，将转换波地震数据与测井数据联系起来。由于弹性阻抗值随着角度变化没有统一的量纲，不利于不同角度的弹性阻抗进行对比，Whitecombe［10］对弹性阻抗做了标准化处理。Gonzalez［11］将转换波反射系数表示成纵波入射角的函数，进而得到转换波弹性阻抗公式，用不同角度转换波弹性阻抗的交会来识别岩性和流体。马劲风［12］、王保丽等［13－15］对弹性阻抗反演都做了大量的研究工作。崔杰等［16］研究了各向异性介质中的转换波弹性阻抗，并且分析了各向异性参数对转换波弹性阻抗的影响。陈天胜等［17］对纵横波联合反演方法做了相应的研究。

笔者选取合适的转换波弹性阻抗公式，对选取转换波弹性阻抗进行标准化处理；在此基础上探索研究纵横波弹性阻抗联合反演方法，并且选用二维Marmousi模型和实际井模型，在合成角度道集添加信噪比（S/N）为3的随机噪声，对该反演算法进行试算；最后从反演的弹性阻抗和转换波弹性阻抗体中提取了精确的弹性参数。

1 纵横波弹性阻抗联合反演

1.1 基本原理

1.1.1 纵横波弹性阻抗定义

Connolly［6］在1999年率先提出了弹性阻抗的概念，并在Aki－Richards近似式［2］的基础上推导了弹性阻抗的表达式，将弹性阻抗EI表示为入射角θ、纵波速度vP、横波速度vS及密度ρ的函数：

其中：

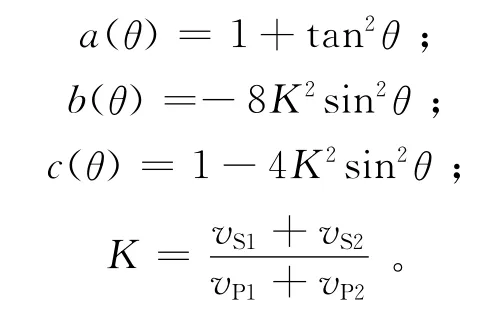
式中：vP1、vS1为分界面上部介质的纵波速度和横波速度；vP2、vS2为分界面下部介质的纵波速度和横波速度（图1）。

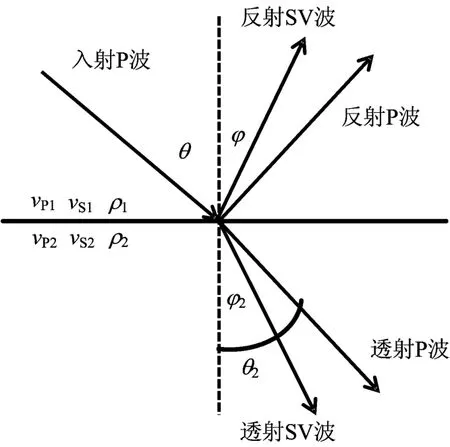
图1 弹性波在弹性界面上的反射与透射Fig.1 Reflection and transmission on elastic interface

Duffaut［9］在转换波反射系数近似的基础上，推导了转换波弹性阻抗公式：

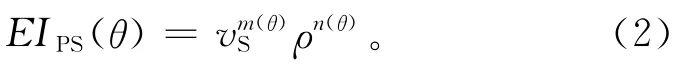
式中：

2006 年，Gonzalez［11］利用 Aki－Richards［2］近似将转换波弹性阻抗公式表示成入射角θ的函数形式：

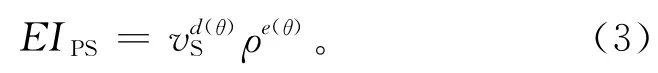
式中：

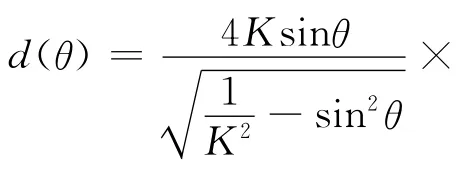
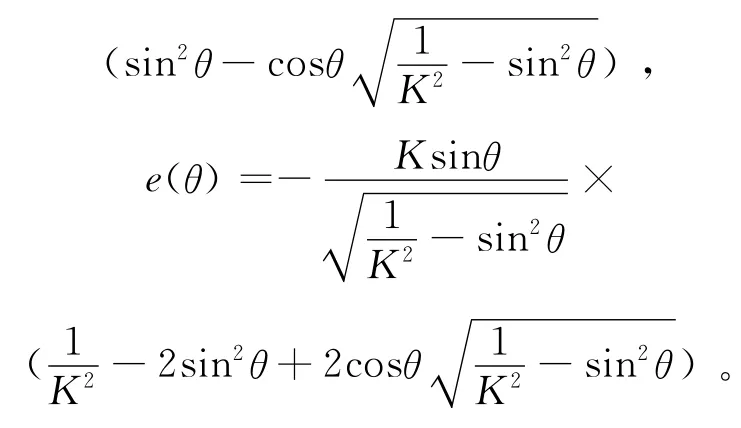
利用Goodway（1997）三层含气砂岩与页岩模型［1］（参数见表1），将由Zoeppritz方程得到的精确转换波反射系数、由Aki－Richards近似得到的转换波反射系数及由转换波弹性阻抗得到的反射系数进行对比，图2是转换波反射系数曲线对比图。可以看出，在小角度情况下，由Duffaut转换波弹性阻抗得到的反射系数比由Gonzalez转换波弹性阻抗得到的反射系数更加接近Zoeppritz方程得到的反射系数，且方程形式更加简单。因此，采用Duffaut推导的转换波弹性阻抗公式。

表1 Goodway模型参数Table 1 Parameters of Goodway model

1.1.2 纵横波弹性阻抗标准化

Whitecombe［10］于2002年对弹性阻抗进行标准化处理，消除了入射角对弹性阻抗尺度的影响。弹性阻抗标准化公式如下：

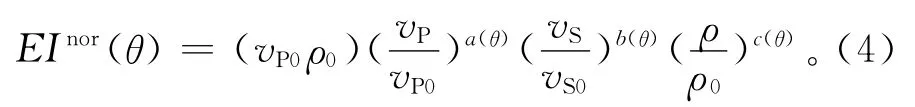
其中：

式中：vPi，vSi和ρi（i＝1，…，N）分别是第i个采样点的纵波速度、横波速度及密度。

同理，笔者对转换波弹性阻抗也进行标准化处理：

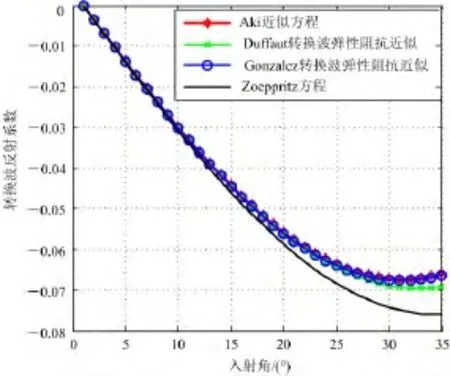
图2 Goodway模型不同近似的转换波反射系数Fig.2 Different PS wave approximate reflection coefficients of Goodway model

1.2 反演流程

王保丽等［15］提出了弹性阻抗反演的基本流程。笔者针对纵横波弹性阻抗联合反演，提出了以下反演流程（图3），包括纵波角度道集和转换波角度道集的提取、弹性阻抗和转换弹性阻抗的计算、地震子波的提取和纵横波弹性阻抗反演等步骤。

1）纵波角度道集和转换波角度道集的提取。在进行纵横波弹性阻抗联合反演之前，需提取不同角度的纵波地震数据体和转换波地震数据体。对于纵波地震数据体，把共中心点道集转化为共角度道集［18］；对转换波地震数据体，把共转换点道集转换为共角度道集［19］。

2）弹性阻抗和转换波弹性阻抗的计算。根据测井资料的纵波速度、横波速度以及密度利用公式（4）和（5）计算井位置处的弹性阻抗曲线和转换波弹性阻抗曲线。弹性阻抗及转换波弹性阻抗的计算一方面会影响地震子波的提取，另一方面可为纵横波弹性阻抗联合反演提供低频信息，从而可以提高反演的分辨率。

3）地震子波的提取。地震子波的提取条件是使观测地震数据与合成地震记录的误差能量差达到最小。分别提取不同角度的纵波和转换波角度道集的地震子波。地震子波的提取是反演的关键问题之一，会直接影响地震反演的精度［20］。

4）纵波弹性阻抗体和转换波弹性阻抗体反演。获取地震子波和测井处的弹性阻抗曲线和转换波弹性阻抗曲线之后，对不同角度的纵波角度道集和转换波角度道集进行反演，得到弹性阻抗体和转换波弹性阻抗体［13］。

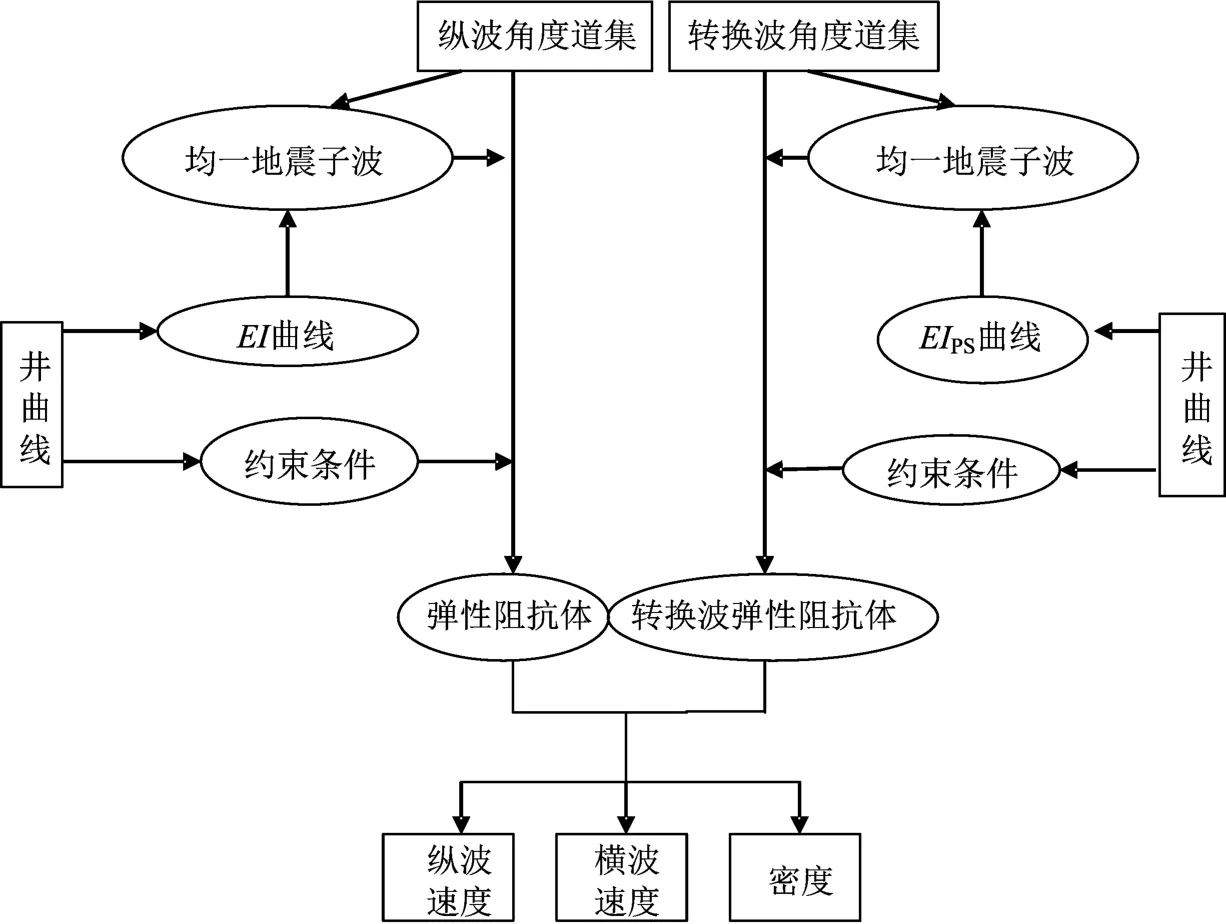
图3 纵横波弹性阻抗联合反演流程Fig.3 Workflow of joint elastic impedance inversion of PP and PS wave

1.3 弹性参数提取

为了将弹性阻抗体和转换波弹性阻抗体与实际的储层预测联系起来，需从弹性阻抗体和转换波弹性阻抗体中提取纵波速度、横波速度及密度等弹性参数。由于每一个采样点处的K值不同，在提取弹性参数时需计算每个采样点处的a（θ），b（θ，K），c（θ，K），m（θ，K），n（θ，K）。对某一采样点处的弹性阻抗和转换波弹性阻抗作线性化处理，即对式（4）和（5）两边取对数，有

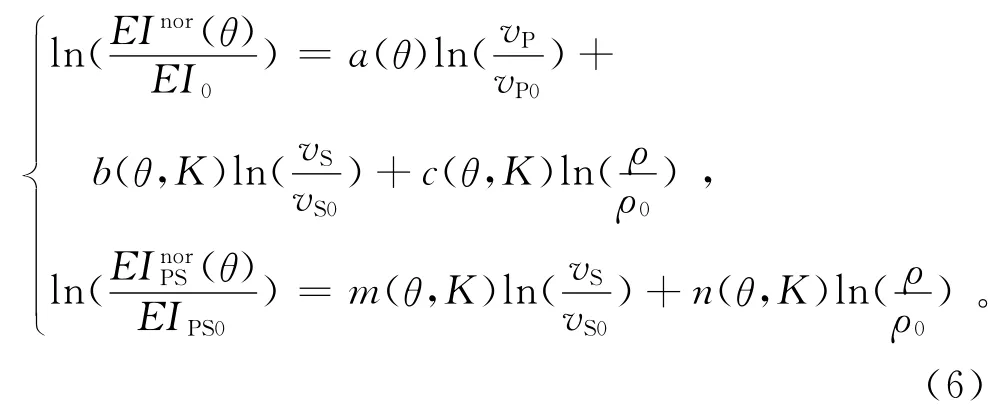
式中：EI0＝vP0ρ0，EIPS0＝vS0ρ0。

在不同角度入射的情况下，所有采样点线性化处理的弹性阻抗和转换波弹性阻抗可以写成矩阵形式，即：

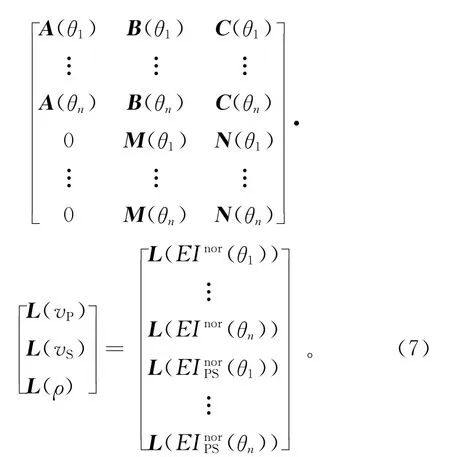
其中：

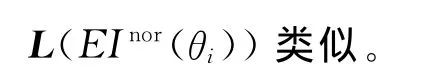
式中：θn为第n个入射角；diag表示对角矩阵。

通过求解上述矩阵，可以从弹性阻抗体和转换波弹性阻抗体中提取纵波速度、横波速度和密度等弹性参数，进一步识别储层特征。

2 二维模型及实际井模型测试

2.1 2D模型纵横波弹性阻抗联合反演

根据纵横波弹性阻抗联合反演的基本原理，利用Marmousi2模型得到合成角度道集，并在PP和PS角度道集分别加入了SNR为3的随机噪音，对该反演算法进行模型测试。图4是CDP 42（common depth point，CDP）正演得到的纵波角度道集和转换波角度道集（用PP波时间表示）；图中圆圈内是气层在不同角度下的地震特征，较其他层段反射振幅更加明显。图5是抽取CDP42处不同角度的弹性阻抗和转换波弹性阻抗的反演结果；从图中可以看出，不同角度的弹性阻抗和转换波弹性阻抗反演结果与原始值吻合程度较高。图6是由纵横波弹性阻抗联合反演和由单纯纵波弹性阻抗反演提取的弹性参数与真实值的对比；结果显示，纵横波弹性阻抗联合反演得到的弹性参数比单纯纵波弹性阻抗反演精度高，特别是密度曲线更加稳定，提取的弹性参数与真实值吻合更好。

图7是不同角度的纵波和转换波角度叠加剖面（用PP波时间表示）；在纵波角度叠加剖面中，蓝色圈内地震反射振幅明显增加，为主要的含气储层，但是该储层在转换波角度叠加剖面中没有响应；这是因为转换波对流体的变化不敏感。图8是纵横波弹性阻抗联合反演得到的不同角度的弹性阻抗剖面和转换波弹性阻抗剖面；在弹性阻抗剖面和转换波弹性阻抗剖面中均能清楚地显示气层所在的位置，这为下一步弹性参数的提取提供了数据基础。图9是经纵横波弹性阻抗联合反演提取的弹性参数（纵波速度、横波速度和密度）剖面与模型剖面对比；结果显示，纵横波弹性阻抗联合反演的弹性参数估计值与真实值基本吻合，能够准确反映岩层信息和流体信息。

2.2 实际井模型的纵横波弹性阻抗联合反演

对某实际工区A井建立模型，在PP和PS角度道集加入S/N为3的随机噪音进行反演，验证该反演方法的有效性。图10是正演得到的纵波和转换波角度道集（用PP波时间表示）。从该图中可以看出，时间为2.0～2.1s时，振幅随入射角的变化有明显的变化，为主要的储层段；表明利用该特征进行叠前纵横波弹性阻抗联合反演可以较好地识别储层。图11是不同角度弹性阻抗和转换波弹性阻抗的反演结果，图中显示估算值与真实值匹配程度较高。图12是从弹性阻抗和转换波弹性阻抗中提取的弹性参数与真实值的对比。可见，复杂的实际井资料模型，也能得到较好的反演结果。

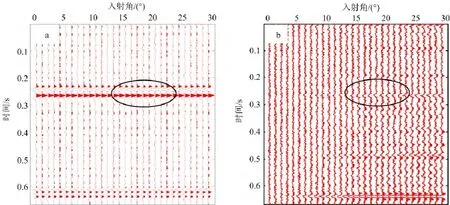
图4 正演得到的角度道集（用PP波时间表示）Fig.4 Pre－stack synthetic seismogram（represented by PP wave time）

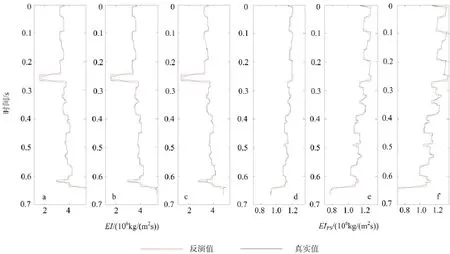
图5 CDP 42处弹性阻抗（a，b，c）及转换波弹性阻抗（d，e，f）反演结果Fig.5 Inversion result of EI（a，b，c）and EIPS（d，e，f）in CDP 42

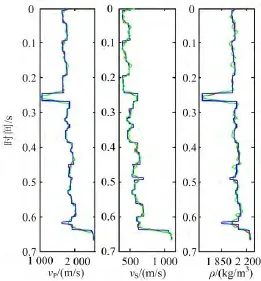
图6 CDP 42纵横波弹性阻抗联合反演（红色曲线）及单纯纵波弹性阻抗反演（绿色曲线）提取的弹性参数与真实值（蓝色曲线）对比Fig.6 Comparison of joint PP and PS EI inversion（red curve）and single PP EI inversion（green curve）with original data（blue curve），elastic parameters extracted fromEI and EIPSin CDP 42

3 结语

在选取精确的转换波弹性阻抗公式的基础上进行纵横波弹性阻抗联合反演方法研究，建立纵横波弹性阻抗联合反演流程，该方法充分利用了纵波和转换波的地震数据，既能较好地利用叠前信息，又具有较高的反演分辨率。

二维模型以及实际井资料模型反演结果表明，纵波弹性阻抗和转换波弹性阻抗反演精度较高，从中提取的纵波速度、横波速度及密度等弹性参数的估测值与真实值之间吻合程度很好，尤其是密度反演更加精确，克服了常规地震反演中密度反演精度不高的缺点，为储层预测和流体识别提供了可靠的地球物理依据。

在反演中依然存在以下问题需要进一步研究：转换波由偏移距道集转化为角度道集的算法；就实际资料而言，反演之前横纵波速度比K的确定。

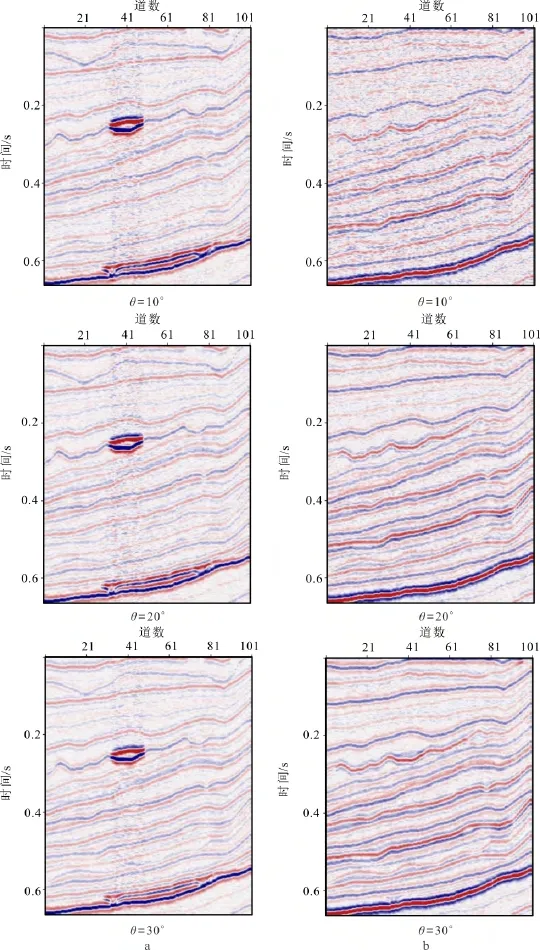
图7 纵波角度叠加剖面（a）和转换波角度叠加剖面（b）Fig7 PP wave angle stacked sections（a）and PS wave angle stacked sections（b）

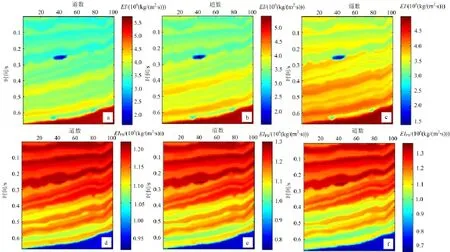
图8 弹性阻抗（a，b，c）及转换波弹性阻抗（d，e，f）反演结果Fig.8 Inversion result of EI（a，b，c）and EIPS（d，e，f）

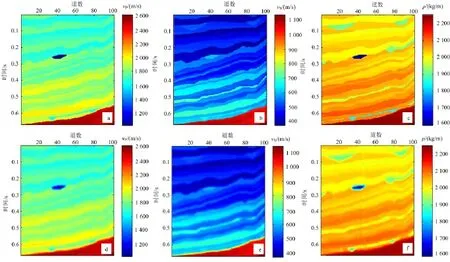
图9 弹性参数真实值（a，b，c）与反演值（d，e，f）Fig.9 Real elastic parameters（a，b，c）and inverted elastic parameters（d，e，f）

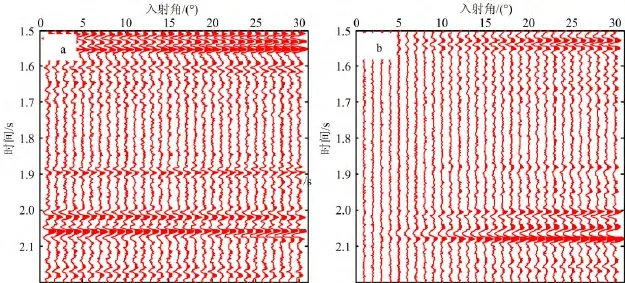
图10 正演得到的角度道集（用PP波时间表示）Fig.10 Pre－stack synthetic seismogram（representecl by PP wave time）

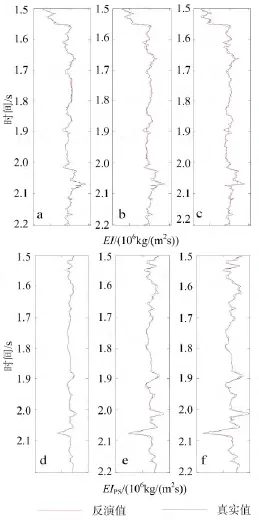
图11 弹性阻抗（a，b，c）及转换波弹性阻抗（d，e，f）反演Fig.11 Inversion result of EI（a，b，c）and EIPS（d，e，f）

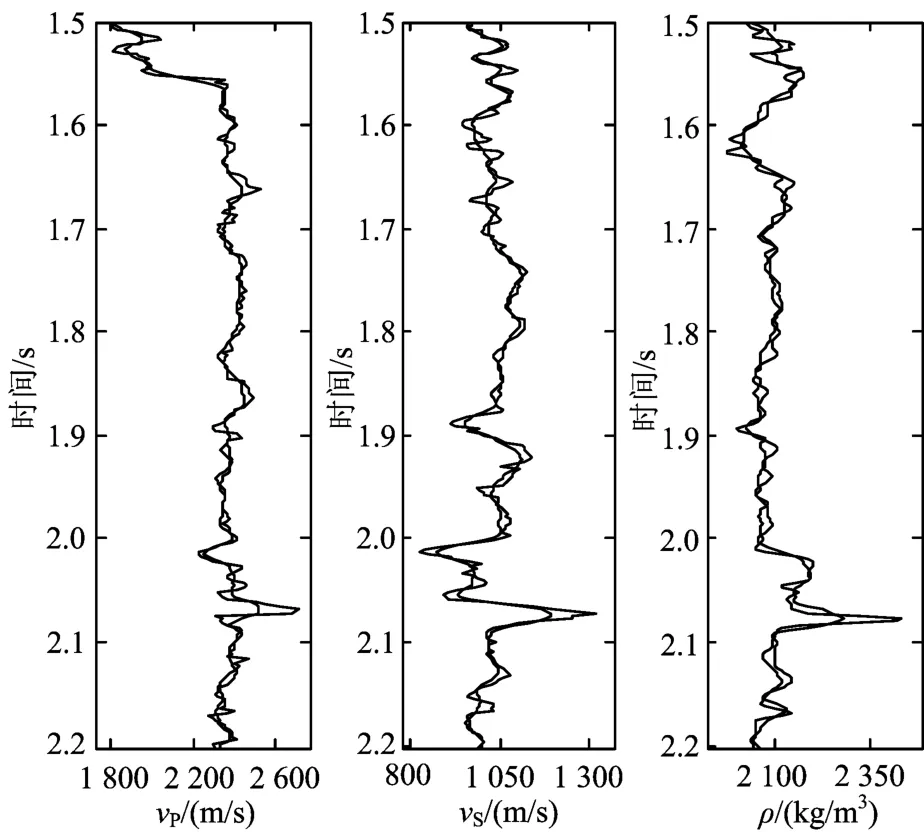
图12 纵横波弹性阻抗联合反演提取的弹性参数（红色曲线）与真实值（蓝色曲线）对比Fig.12 Comparison of joint PP and PS EIinversion（red curve）with original data（blue curve），elastic parameters extracted fromEI and EIPS

（References）：

［1］印兴耀，张繁昌，孙成禹.叠前地震反演［M］.青岛：中国石油大学出版社，2010：34－56.Yin Xingyao， Zhang Fanchang， Sun Chengyu.Prestack Seismic Inversion［M］.Qingdao：China Universtiy of Petroleum Press，2010：34－56.

［2］Aki K，Richards P.Quantitative Seismology：Theory and Methods［M］.Mill Valley：University Science Books，1980.

［3］张广智，王丹阳，印兴耀，等.基于 MCMC叠前地震反演方法研究［J］.地球物理学报，2011，54（11）：2926－2932.Zhang Guangzhi，Wang Danyang，Yin Xingyao，et al.Study on Prestack Seismic Inversion Using Markov Chain Monte Carlo［J］.Chinese Journal of Geophysics，2011，54（11）：2926－2932.

［4］陈建江，印兴耀，张广智.层状介质AVO叠前反演［J］.石油地球物理勘探，2006，41（6）：656－662.Chen Jianjiang， Yin Xingyao， Zhang Guangzhi.Prestack AVO Inversion of Layered Medium［J］.Oil Geophysical Prospecting，2006，41（6）：656－662.

［5］张广智，陈怀震，印兴耀，等.基于各向异性AVO的裂缝弹性参数叠前反演方法［J］.吉林大学学报：地球科学版，2012，42（3）：845－851.Zhang Guangzhi，Chen Huaizhen，Yin Xingyao，et al.Method of Fracture Elastic Parameter Inversion Based on Anisotropic AVO［J］.Journal of Jilin University：Earth Science Edition，2012，42（3）：845－851.

［6］Connolly P.Elastic Impedance［J］.The Leading Edge，1999，18（4）：438－452.

［7］Larsen J.AVO Inversion by Simultaneous PP and PS Inversion［D］.Calgary：University of Calgary，1999：9－37.

［8］Milos S.Elastic Impedance Inversion in Practice［C］//SEG Technical Program Expanded Abstracts.Calgary：［s.n.］，2000：689－692.

［9］Duffaut K，Martin L.Shear－Wave Elastic Impedance［J］.The Leading Eadge，2000，19（11）：1222－1229.

［10］Whitecombe D.Elastic Impedance Normalization［J］.Geophysics，2002，67（1）：60－62.

［11］Gonzalez E.Physical and Quantitative Interpretation of Seismic Attribute for Rocks and Fluids Identification［D］.Alto：Stanford University，2006：6－35.

［12］马劲风.地震勘探中广义弹性阻抗的正反演［J］.地球物理学报，2003，46（1）：118－124.Ma Jinfeng.Forward Modeling and Inversion Method of Generalized Elastic Impedance in Seismic Exploration［J］.Chinese Journal of Geophysics，2003，46（1）：118－124.

［13］王保丽，印兴耀，张繁昌.弹性阻抗反演及应用研究［J］.地球物理学进展，2005，20（1）：89－92.Wang Baoli，Yin Xingyao，Zhang Fanchang.Elastic Impedance Inversion and Its Application［J］.Progress in Geophysics，2005，20（1）：89－92.

［14］王保丽，印兴耀，张繁昌，等.基于Fatti近似的弹性阻抗方程反演［J］.地球物理学进展，2008，23（1）：192－197.Wang Baoli，Yin Xingyao，Zhang Fanchang，et al.Elastic Impedance Equation Based on Fatti Approximation and Inversion［J］.Progress in Geophysics，2008，23（1）：192－197.

［15］王保丽，印兴耀，张繁昌，等.基于Gray近似的弹性波阻抗方程及反演［J］.石油地球物理勘探，2007，42（4）：435－439.Wang Baoli，Yin Xingyao，Zhang Fanchang，et al.Gray Approximation Based on Elastic Wave Impedance Equation and Inversion［J］.Oil Geophysical Prospecting，2007，42（4）：435－439.

［16］Cui Jie，Han Liguo，Liu Qiankun，et al.P－SV Wave Elastic Impedance and Fluid Identification Factor in Weakly Anisotropic Media［J］.Applied Geophysics，2010，7（2）：135－142.

［17］陈天胜，刘洋，魏修成.纵波和转换波联合AVO反演方法研究［J］.中国石油大学学报：自然科学版，2006，26（1）：33－37.Chen Tiansheng，Liu Yang，Wei Xiucheng.Joint Amplitude Versus Offset Inversion of P－P and P－SV Seismic Data［J］.Journal of China University of Petroleum：Edition of Natural Science，2006，26（1）：33－37.

［18］张广智，王文龙，印兴耀，等，基于射线理论的角度道集提取方法综述［J］.地球物理学进展，2011，26（5）：1696－1670.Zhang Guangzhi，Wang Wenlong，Yin Xingyao，et al，Overview of Extraction Methods of Angle Gathers Based on Ray Theory［J］.Progress in Geophysics，2011，26（5）：1696－1707.

［19］Tessmer G.Processing of PS－Reflection Data Applying a Common Conversion Point Stacking Technique［J］.Geophysical Prospecting，1990，38：267－286.

［20］张广智，刘洪，印兴耀.井旁道地震子波精细提取方法［J］.石油地球物理勘探，2005，40（2）：158－162.Zhang Guangzhi，Liu Hong，Yin Xingyao，Method for Fine Picking up Seismic Wavelet at Uphole Trace［J］.Oil Geophysical Prospecting，2005，40（2）：158－162.