圆弧齿形单螺杆式水力机械的啮合原理及应用

李增亮,石白妮,鲁佳琪,黄立杰

(1.中国石油大学机电工程学院,山东青岛 266580;2.中石油长庆油田公司,陕西西安 710021; 3.中石油西南管道公司,四川成都 610041;4.济南外国语学校三箭分校,山东济南 250107)

圆弧齿形单螺杆式水力机械的啮合原理及应用

李增亮1,石白妮2,鲁佳琪3,黄立杰4

(1.中国石油大学机电工程学院,山东青岛 266580;2.中石油长庆油田公司,陕西西安 710021; 3.中石油西南管道公司,四川成都 610041;4.济南外国语学校三箭分校,山东济南 250107)

分析用于单螺杆式水力机械的圆弧齿形成形原理,阐述求共轭齿形曲线的内滚包络法和齿廓法线法,提出圆弧齿形的定转子断面面积、过流面积的计算方法,用圆弧齿形进行采油用螺杆泵实例设计;同时对该实例进行容积效率预测。结果表明:提出的原始齿形曲线的设计方案和数学方程正确可用,圆弧齿形不仅齿形简单且曲率容易控制,对设计加工制造很有利;三头采油用圆弧齿形螺杆泵在设计压差下容积效率超过97%,能够满足设计要求。

圆弧齿形;单螺杆;啮合原理;内滚包络法;曲率;容积效率

单螺杆式水力机械在润滑系统、固液混输、油气混输、螺杆泵人工举升系统及井下动力螺杆钻具方面有重要应用[1-4]。在螺杆式水力机械设计中,螺杆马达与螺杆泵是该系统的核心部件,其定、转子齿形的设计体现了该型机械的设计水平[5-7]。国外较常用的断面齿形主要为普通内摆线等距线型[8-9],但该种线型共轭骨线副上不可避免地存在曲率半径为零的点,螺杆衬套副磨损较快,影响寿命。中国主要以短副内摆线等距线型、短幅外摆线等距线型为主,短副外摆线等距线型表现出较好的工作性能,但参数取值范围过小,不适宜多头螺杆机械的设计制造[10-12]。笔者提出圆弧齿形的定转子断面面积、过流面积的计算方法,通过内滚包络法和齿廓法线法分别计算其共轭齿形,并给出设计实例。

1 原始齿形曲线

1.1 两圆的极坐标方程

如图1所示,该齿形的原始齿形曲线由两段外切的圆弧组成,外凸的圆弧称为凸圆,内凹的圆弧称为凹圆,设螺杆线数为N,定子线数为n=N+1,两圆心与原点连线的夹角为π/N,即在一个圆周2π中形成N个齿瓣,求得该角度内的原始齿瓣曲线,通过坐标变换可以得到其余齿瓣曲线。

极坐标用极径和极角来表示点在坐标系中的位置,由圆的极坐标表达式可知:当圆心极坐标为(ρ′,θ′),半径为R时,圆在极坐标系中的表达式为

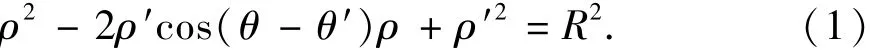
图1 圆弧齿形的原始齿形曲线Fig.1 Original arc tooth profile curve

设凸圆半径为R1,圆心极坐标(d1,π/2),凹圆半径R2,圆心极坐标(d2,π/2-π/N),带入式(1),可得到两圆极径为

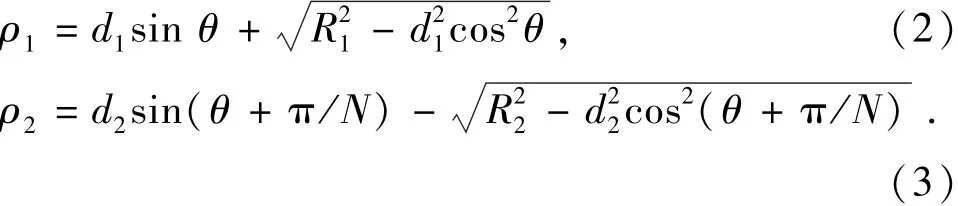
1.2 两圆外切的充要条件

在两圆的极坐标方程中存在4个变量:分别为两圆半径R1、R2和两圆圆心到原点的距离d1、d2。在已知R1、d1、d2后,求在角度π/N内与凸圆相切的凹圆半径R2,必须满足两圆外切的充要条件:O1O2=R1+R2。

由余弦定理可知:

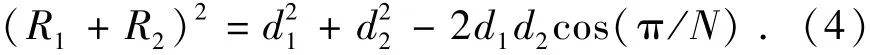
从而

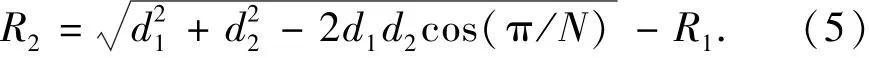
1.3 两圆外切时的临界角

当凸圆与凹圆外切时,设切点为M,与y轴的夹角θ′定义为外切临界角,此时∠OMO1和∠OMO2互为补角,根据正弦定理有

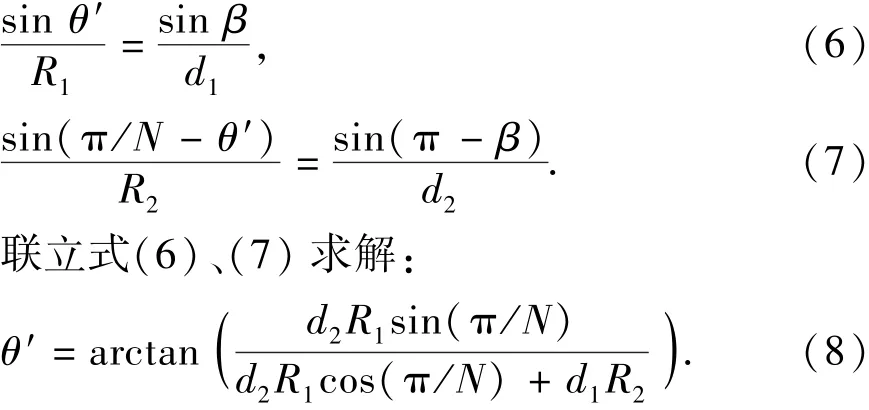
临界角是关于R1、R2、d1、d2、N的函数,当这些变量确定时,两圆外切临界角是一个定值。

1.4 原始齿形曲线方程

根据以上分析可以得到原始齿形曲线方程:

2 内滚包络法

平面行星运动可以看做为两个瞬心圆的相对纯滚动[13-15],假设发生线ρ(θ)做如下行星运动:偏心距为E,以ρ(θ)的包心法导圆NE做动瞬心圆,带着ρ(θ)沿定瞬心圆nE做相对纯滚动,其本质等价于两个运动的叠加。图2为内滚法原理图。

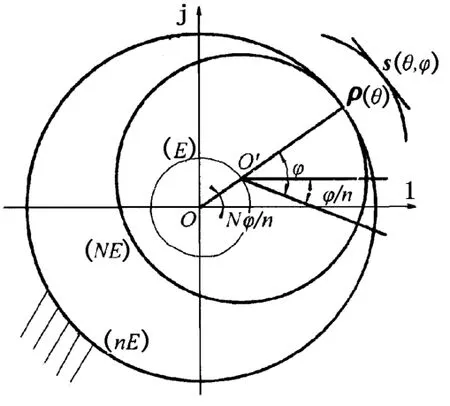
图2 内滚法原理图Fig.2 Principle diagram of inside rolling envelope method

如图2,ρ(θ)绕O′点自转,自转角为φ/n,φ是时间和角速度的函数。同时O′绕定坐标系原点O做半径为E的圆周运动,即ρ(θ)绕着O做偏心距为E的公转,其公转角为-Nφ/n,二者运动方向相反,则转子齿形ρ(θ)的运动方程为

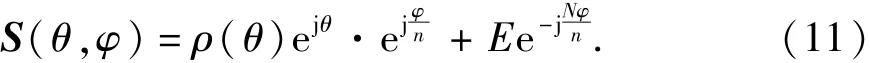
求原始齿形曲线运动方程的意义在于可以得到原始齿形做行星运动任意时刻的位置,从而由该运动方程得到齿形做行星运动时的包络区,如果ρ(θ)为三头圆弧齿形,则其通过运动方程得到的包络区如图3阴影所示,包络区的外包络线即为要求的共轭齿形曲线。图4为复矢量的平行示意图。

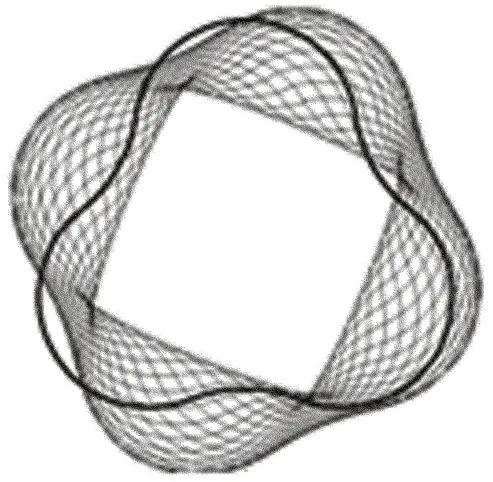
图3 由内滚法生成的包络区Fig.3 Envelope area using inside rolling method

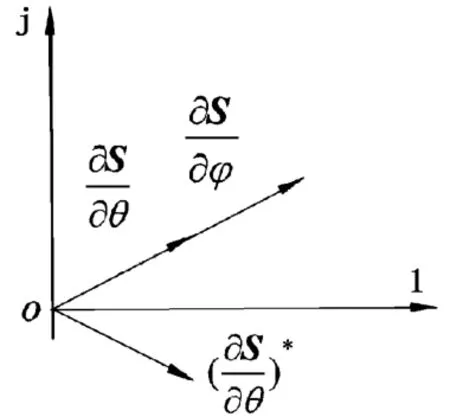
图4 复矢量的平行Fig.4 Parallel of complex vector

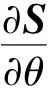
解方程即可得到共轭齿形曲线转角φ和原始齿形曲线转角θ的关系为

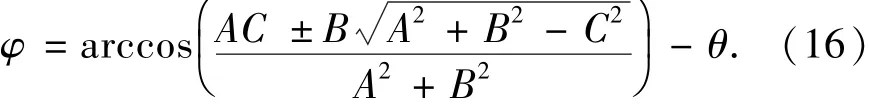
联立式(10)、(16)可以得到共轭齿形曲线的复矢量方程。

基于包络原理的包络法求解过程体现了形成啮合齿形的根本原理,但求解过程较为复杂。

3 齿形法线法求共轭齿形曲线

基于啮合原理的齿形法线法相比包络法较为简便,更适用于工程实际[16-18]。

设坐标系XPY为定坐标系,与轮1和轮2固连的坐标系X1O1Y1、X2O2Y2为动坐标系。ρ为轮1上的原始齿形曲线,P为两轮的节点。如图5所示,齿形ρ上的接触点M的法线通过节点P,M1点是齿形ρ上任一点,过该点作齿形ρ的法线M1L1,与轮1的节圆交于P1点。当M1成为接触点时,P1点与节圆P重合,假设固连在轮1上的动坐标系X1O1Y1连同齿形ρ沿逆时针方向转过角度φ1,设M1坐标为(x1,y1),γ为齿形ρ在M1点的切线与X1轴的夹角。

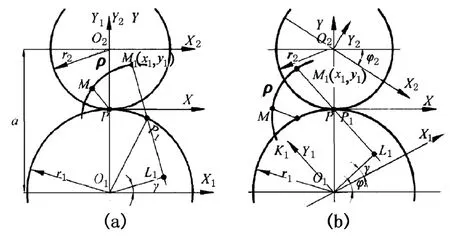
图5 齿形法线法原理图Fig.5 Principle diagram of tooth profile normal method

两圆在直角坐标系中的参数方程为

由式(17)可得圆弧齿形切线的斜率为

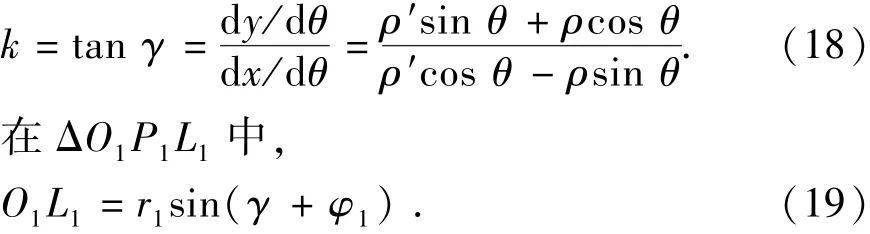
又已知M1点的坐标值及齿廓ρ的斜率,可以求得法线方程,由点到直线的距离方程可以求得

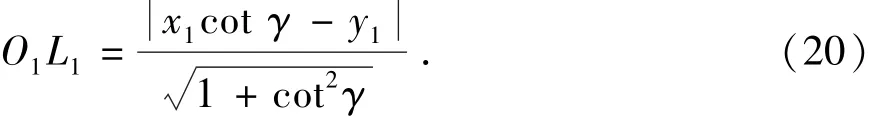
联立式(18)、(19)可以得到φ1的计算公式:

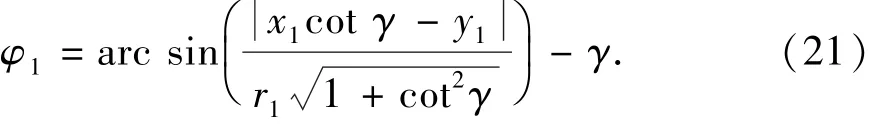
这样便确定了M1点位置与齿形转角间的关系。

将接触点坐标(x1,y1)变换到与轮2固连的动坐标系X2O2Y2中,就可求得共轭齿形S的表达式。

将M1点坐标(x1,y1)变换到静坐标系XPY中,得到(x,y),由坐标变化的矩阵公式可知:

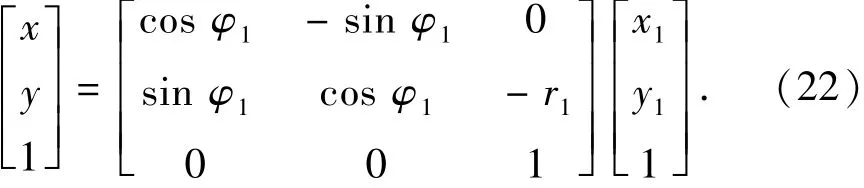
对(x,y)应用坐标变换求得其在动坐标系X2O2Y2中的表达式,φ2为轮2相对转过的角度,在螺杆泵中转子的自转与公转方向相反,则令i12=-

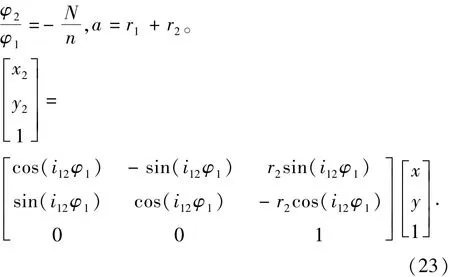
所以轮2的坐标系X2O2Y2和轮1坐标系X1O1Y1之间的坐标关系变化如下:

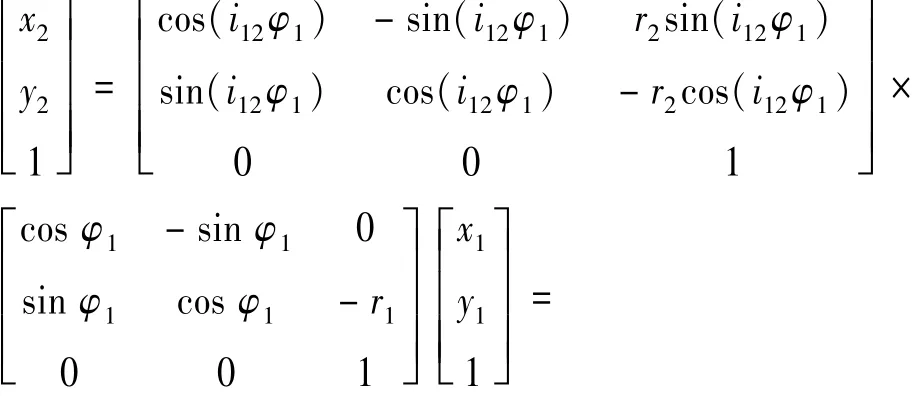
4 圆弧齿廓参数分析

4.1 过流面积计算

转子断面齿形的面积为

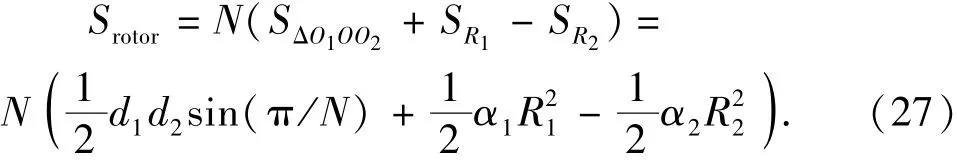
由正弦定理可知:

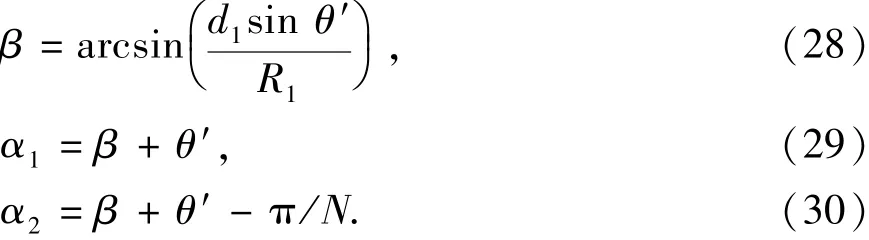
联立式(27)、(28)、(29)、(30),可求得转子断面面积。

在实际求解过程中发现,积分求解定子断面面积公式非常复杂,没有工程实用价值,研究分析中发现圆弧共轭齿形的形状主要由凸圆顶点决定,该顶点初始极坐标为(R1+d1,π/2),所以在简化求解定子断面面积时可以近似考虑为凸圆齿形顶点做行星运动之后形成的外包络。其复矢量方程为

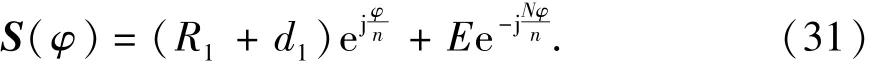
如图6所示,设复平面中有复矢量S(φ),参数φ增大dφ时,S有增量dS,则微分三角形的面积dA可由下式求得:

式中,dS*为dS的共轭复矢量。

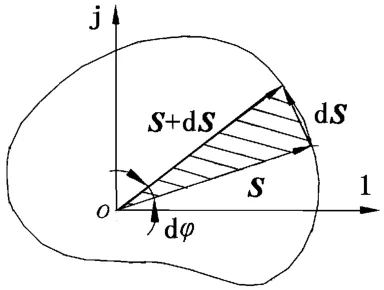
图6 复矢量法求解面积示意图Fig.6 Sketch map of solving area using complex vector method

沿着封闭曲线C积分,可得到曲面C所围成的面积A:

根据以上方法求得定子的近似断面面积为则过流面积为

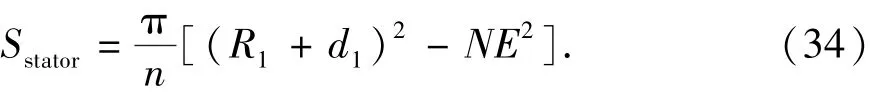
4.2 曲率半径分析

圆弧齿形不仅齿形简单且曲率容易控制。传统摆线线型的曲率半径基于很多变量,如导圆半径、滚圆半径、头数、偏心距及等距圆半径,所以设计摆线线型时,必须考虑曲线曲率半径取零时各参数的极限值,这样可以得到圆滑的摆线曲线。而圆弧线型因为原始齿形由两段圆弧相切组成,所以曲率半径分别为圆弧半径R1、R2,通过调整圆弧半径得到接触效果很好的原始齿形,这也是摆线线型无法比拟的优势。

5 圆弧齿形螺杆泵设计实例

5.1 实例的参数设计

设计采油用三头圆弧齿形螺杆泵,流量为100 m3/d,输送油液密度为920 kg·m-3,泵外径为122 mm,单级增压值设为0.7 MPa,级数为7级,偏心距为5 mm,凸圆与凹圆半径分别为30、70 mm,两圆心距离原点的距离分别为15、30 mm,同时设容积效率为0.96,机械效率为0.8,计算得到该泵的定子导程为480 mm,过流面积为1 122 mm2,转速为43.4 r/min-1,轴向力和扭矩分别为10.2 kN和178 N· m。

5.2 容积效率曲线预测

螺杆泵常根据经验公式初步估计泵性能[18],该公式只与泵的结构参数及定转子的配合间隙有关,与所采用线型无关,可以用它来进行圆弧齿形螺杆泵容积效率的预测。

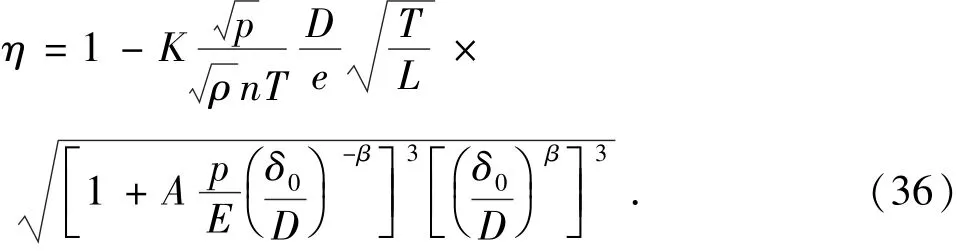
式中,K为容积损失系数,此处取为2.45×10-6;ρ为油液密度,kg/m3;n为转速,r/min;T为定子导程, m;D为转子断面直径,m;e为偏心距,m;A为与衬套橡胶层厚度有关的常数,取为375;L为衬套有效长度,取为3.36 m;δ0为螺杆衬套初始过盈值,取为0.2 mm;E为衬套用橡胶的弹性模量,取为6 MPa;β为与橡胶弹性模量有关的常数,取为0.83。

图7为容积效率预测。由图7可知,泵进出口压差值由1 MPa增大到3 MPa时,容积效率接近100%,处于高效区,3 MPa以后容积效率显著降低,但在设计压差下容积效率依然高于97%,说明该设计能够满足设计要求。

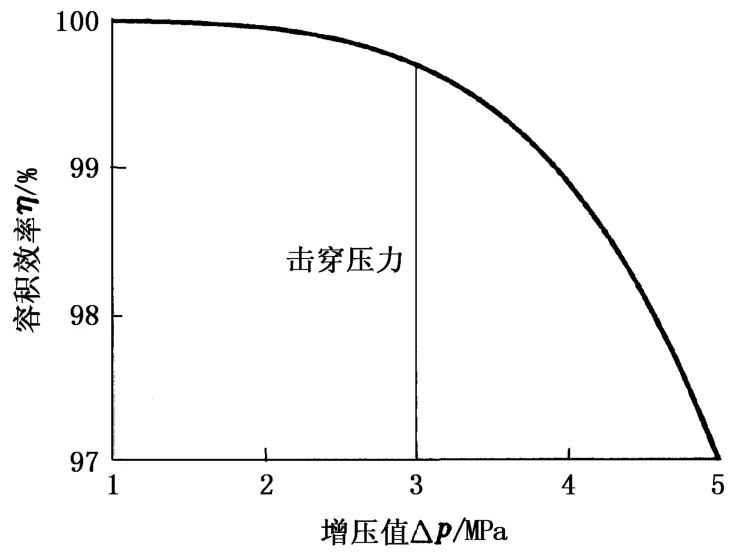
图7 容积效率预测Fig.7 Prediction of volumetric efficiency

6 结束语

应用共轭齿形曲线的内滚包络法和齿廓法线法得到了其共轭齿形的极坐标方程和直角坐标方程。圆弧齿形不仅齿形简单且曲率容易控制。提出的原始齿形曲线设计方案和数学方程正确可用。应用圆弧齿形设计了三头采油用圆弧齿形螺杆泵,凸圆与凹圆半径分别为30、70 mm,两圆心到原点的距离分别为15、30 mm。螺杆泵压差由1 MPa增大到3 MPa时,容积效率接近100%,处于高效区,3 MPa以后容积效率显著降低,但在设计压差下容积效率仍然高于97%,说明该设计能够满足设计要求。

[1] 徐敏,陈家庆,王丽,等.螺杆式水力机械及其在石油石化行业中的应用[J].北京石油化工学院学报, 2004,12(1):1-7.

XU Min,CHEN Jiaqing,WANG Li,et al.Screw-type hydraulic machinery and its application in petroleum and petro-chemical industry[J].Journal of Beijing Institute of Petro-Chemical Technology,2004,12(1):1-7.

[2] 李明谦,黄继庆.螺杆钻具的应用现状及未来发展建议[J].石油机械,2006,34(5):73-76.

LI Mingqian,HUANG Jiqing.The present situation of the application of screw drill tool and the future development suggestions[J].China Petroleum Machinery,2006, 34(5):73-76.

[3] 安永生,宋扬,张德实,等.螺杆泵转子三维运动仿真分析及型线优化设计[J].中国石油大学学报:自然科学版,2012,36(3):155-158.

AN Yongsheng,SONG Yang,ZHANG Deshi,et al. Three dimensional motion simulation and locus optimization design of progressive cavity pump rotor[J].Journal of China University of Petroleum(Edition of Natural Science),2012,36(3):155-158.

[4] LEA J F,ANDERSON P O,ANDERSON D G.Optimization of progressive cavity pump systems in the development of the clearwater heavy oil reservoir[J].Journal of Canadian Petroleum Technology,1988,27(1):1-5.

[5] 彭勇.螺杆泵采油系统杆柱的扭转振动特性分析[J].石油矿场机械,2001,30(2):5-8.

PENG Yong.The twisting vibration characteristic analysis of the sucker rod string for progressing cavity pump oil production system[J].Oil Field Equipment,2001,30 (2):5-8.

[6] SAVETH K J.Field study of efficiencies between progressing cavity,reciprocating,and electric submersible pumps[R].SPE 25448,1993.

[7] 苏义脑,于炳忠,谢竹庄.单螺杆钻具马达线型分析[J].石油学报,1986,7(4):95-109.

SU Yinao,YU Bingzhong,XIE Zhuzhuang.Analysis of conjugate contours in matching stator-rotor cross-section of moineau-type positive displacement drilling motor[J]. Acta Petrolei Sinica,1986,7(4):95-109.

[8] SAMUEL G R,SAVETH K.Progressing cavity pump (PCP):new performance equations for optimal design [R].SPE 39786,1998.

[9] CHOLET H.Progressing cavity pump[M].Paris:Editions Technip,1997:20-31.

[10] 孙兴伟,王巧云,王可.多头单螺杆泵转子和定子的参数化建模[J].组合机床与自动化加工技术,2009 (9):73-75.

SUN Xingwei,WANG Qiaoyun,WANG Ke.Parameter modeling of rotor and stator of multiple single screw pump[J].Modular Machine Tool&Automatic Manufacturing Technique,2009(9):73-75.

[11] 刘成林,王世杰.多头单螺杆泵端面线型设计[J].机械设计与制造,2010(1):36-38.

LIU Chenglin,WANG Shijie.Linear design of long single-screw[J].Machinery Design&Manufacture,2010 (1):36-38.

[12] CHOLET H,VANDENBROUCKE E.Progressive cavity pump with composite stator and manufacturing process: US,6336796[P].2002-01-08.

[13] 苏义脑.螺杆钻具研究与应用[M].北京:石油工业出版社,2001:48-51.

[14] 苏义脑,谢竹庄.单螺杆钻具马达短幅内摆线等距线型分析[J].石油机械,1987,15(6):5-11.

SU Yinao,XIE Zhuzhuang.Study on curtate hypocycloid isometric conjugate contour-pattern of downhole drilling motors[J].China Petroleum Machinery,1987, 15(6):5-11.

[15] 苏义脑,谢竹庄.单螺杆钻具马达短幅外摆线等距线型分析[J].石油机械,1986,14(12):1-8.

SU Yinao,XIE Zhuzhuang.Study on epitrochoidal isometric conjugate contour-pattern of downhole drilling motors[J].China Petroleum Machinery,1986,14(12):1-8.

[16] 万邦烈,曹玉德.短幅内摆线型单螺杆式水力机械的啮合原理[J].华东石油学院学报:自然科学版, 1987,11(4):28-42.

WAN Banglie,CAO Yude.The engagement principle of single-screw hydraulic machinery with hypotrochoid profile[J].Journal of East China Petroleum Institute(Edition of Natural Science),1987,11(4):28-42.

[17] 万邦烈,曹玉德.短幅外摆线等距型单螺杆式水力机械的啮合原理[J].石油大学学报:自然科学版, 1989,13(2):38-49.

WAN Banglie,CAO Yude.The engagement principle of single-screw hydraulic machinery with epitrochoid profile [J].Journal of the University of Petroleum,China(Edition of Natural Science),1989,13(2):38-49.

[18] 万邦烈.单螺杆式水力机械[M].东营:石油大学出版社,1993:96-100.

(编辑 沈玉英)

Meshing theory and application of single screw hydraulic machinery with arc tooth profile

LI Zengliang1,SHI Baini2,LU Jiaqi3,HUANG Lijie4
(1.College of Mechanical Electronic Engineering in China University of Petroleum,Qingdao 266580,China; 2.PetroChina Changqing Oilfield Company,Xi'an 710021,China; 3.PetroChina Southwest Pipeline Company,Chengdu 610041,China; 4.Jinan Foreign Language Sanjian Brand School,Jinan 250107,China)

The forming theory of arc tooth profile used in single screw hydraulic machinery was analyzed.The inside rolling envelope method and the tooth profile normal line method were used to solve the formula of conjugate tooth profile.The flow area and sectional areas of rotor and stator were analyzed.A prototype screw pump using arc tooth profile was designed.The volumetric efficiency of the prototype was predicted.The results show that the proposed design scheme and mathematical formulas of original tooth profile are feasible and correct.The arc tooth profile is very simple and the curvature is easy controlled,it is very beneficial for the design,processing and manufacturing.For the three heads screw pump with arc tooth profile,its volumetric efficiency under the designed pressure difference remains to be above 97%,and it can meet the design requirements.

arc tooth profile;single screw;meshing theory;inside rolling envelope method;curvature;volumetric efficiency

TE 933

A

1673-5005(2014)04-0132-06

10.3969/j.issn.1673-5005.2014.04.019

2013-12-02

中国石化股份公司科技攻关项目(P12133)

李增亮(1962-),男,教授,博士,博士生导师,从事石油机械教学及科研工作。E-mail:lizl@upc.edu.cn。

李增亮,石白妮,鲁佳琪,等.圆弧齿形单螺杆式水力机械的啮合原理及应用[J].中国石油大学学报:自然科学版,2014,38(4):132-137.

LI Zengliang,SHI Baini,LU Jiaqi,et al.Meshing theory and application of single screw hydraulic machinery with arc tooth profile[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(4):132-137.