调制式振动对大斜度井减摩阻影响规律
王 鹏,倪红坚,王瑞和,沈忠厚,李志娜,雷 鹏
(1.中国石油大学石油工程学院,山东青岛 266580;2.中国石油大学地球科学与技术学院,山东青岛 266580)
发展定向井、水平井及大位移井技术开发复杂油气藏、海洋油气资源,是满足对能源的巨大需求的必要手段。在这类大斜度井的钻探过程中,摩阻问题十分突出,研发新型高效的减摩阻技术迫在眉睫[1]。Roper等[2]首次以发明专利的形式提出了在钻斜井过程中使用激振器激发钻柱产生轴向振动,减小钻柱与井壁之间的摩阻,从而提高机械钻速的思路。近几年,国内外开展了相关技术的应用性研究,但主要集中在激振器的研制和配套工艺技术两方面[3-6]。笔者针对激发钻柱产生轴向振动减阻技术,建立考虑振动和摩阻耦合作用的钻柱轴向振动减摩阻数学模型,并分析激振力强度等因素对减阻效果的影响。
1 数学模型的建立
1.1 基本假设
钻柱为线弹性变形,钻柱横截面为等壁厚圆环;井壁为刚性;钻柱包含滑动钻进和静止两种状态,只考虑钻柱在轴向上的动力效应。
1.2 方程的建立
在钻柱上取微元段dx,其在轴向激励下的振动微分方程[7]可表示为
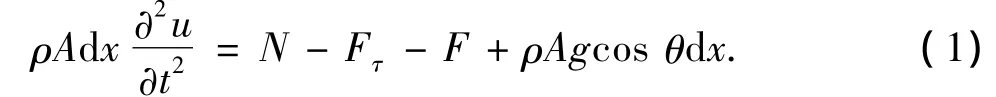
式中,ρ为钻柱的材料密度,kg/m3;A为钻柱截面积,m2;u为钻柱偏离其平衡位置的动态振动位移,m;θ为井斜角,(°);N为轴向内力,N;Fτ为钻柱内外钻井液剪切力,N;F为井壁的摩擦力,N;g为重力加速度,m/s2;t为时间,s。
轴向力 N[7]可表示为

因大多数钻井液属于塑性流型,如按宾汉流体考虑,则钻柱内外钻井液剪切力Fτ[8]为

式中,τ0为动切应力,Pa;μpv为塑性黏度,Pa·s。
钻柱振动对其与井壁之间的摩擦接触状况有显著影响[9],二者之间的关系可表示为

式中,μ和μ0分别为有无振动情况下钻柱与井壁间的摩擦系数;β为摩擦减小系数,其值越小说明振动的减阻效果越好。
假设钻柱以速度v0沿其轴线向井底做匀速滑动,同时以速度vt沿轴向做简谐振动,则β为ξ=v0v
*的函数[10]。在一个振动周期T内,当vt与v0反向且vt大于v0时,钻柱受到的摩擦力方向变为与钻柱宏观滑动方向相同,此时该摩擦力有助于推动钻柱下行,且该摩擦力作用时间为
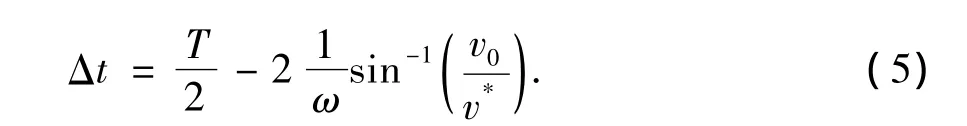
因此,一个周期T内平均摩擦力为
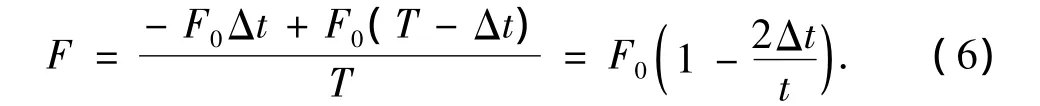
联立式(5)和(6)得考虑钻柱振动时钻柱受到的摩擦力为

式中,F0为无振动时由库伦定律计算的摩擦力,N。
β可表示为

将式(2)、(3)和(7)代入式(1),即可得到钻柱轴向振动偏微分方程为
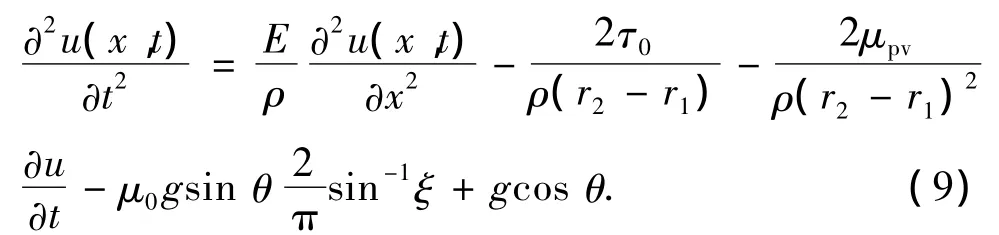
1.3 边值条件
设初始动态振动位移和初始动态振动速度均为零,在钻柱的中点处施加简谐激励,则边界条件和初始条件可表示为
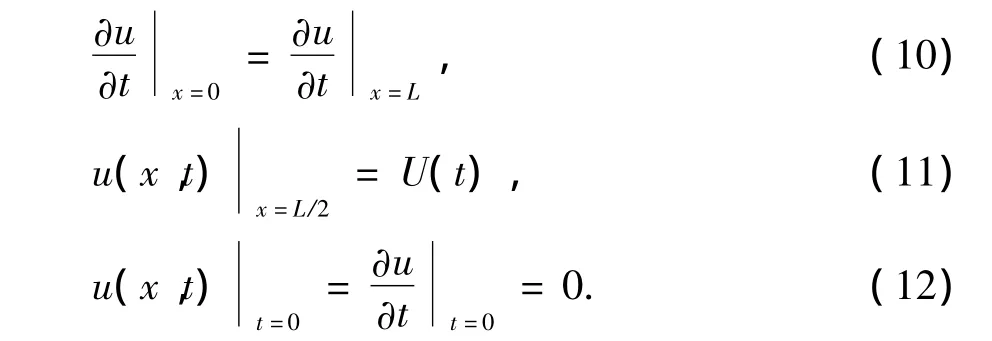
联立式(9)~(12)即可得到大斜度井考虑钻柱重力、振动、钻井液黏滞阻力等因素的钻柱轴向振动减摩阻数学模型。
2 方程求解
利用中心差分法建立钻柱轴向振动偏微分方程的差分方程[7,11]为

边值条件为

求解步骤:给定ξ的初始值,利用差分格式式(13)求得任意t时刻钻柱上各点的位移、速度和加速度,修正参数ξ=v0/v*。重复以上步骤若干次后即可得到钻柱振动的稳态响应,将钻柱上各点处的ξ值代入式(7)积分可求出钻柱受到的摩阻。
3 振动减摩阻规律
影响振动减阻效果的因素主要包括工具参数(主要是激振力强度和激振频率)和钻井工况参数(主要是井壁摩阻系数和钻井液黏滞系数),通过分析以上参数对振动减摩阻的影响,为振动减摩阻技术现场应用过程中参数的选取提供依据,同时对激振工具的研制具有一定的指导意义。
分析计算设定的参数为:沿井眼低边放置长2.5 km钻柱,弹性模量为210 GPa,密度为7 850 kg/m3,钻柱内、外径分别为72和127 mm,在钻柱中点处施加轴向简谐激励,取井斜角θ=78.69°,计算施加振动后和无振动时钻柱所受到的摩擦力比值F/F0、振动钻柱长度L和钻柱中点处振动速度幅值vm。
3.1 单因素影响规律
3.1.1 激振力强度
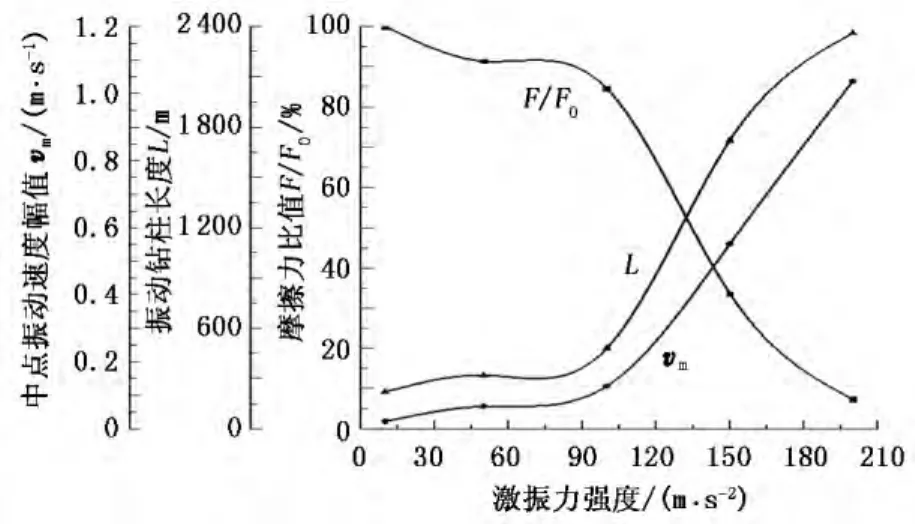
图1 不同激振力强度下的振动减摩阻效果Fig.1 Effect of friction reduction by vibration under different intensities of excitation force
图1为计算得到的激振力强度对摩擦力比值F/F0、振动钻柱长度L和钻柱中点振动速度幅值vm的影响(频率为80 Hz,摩阻系数为0.4,钻井液黏滞系数为10 s-1)。从图1中可以看出,随着激振力强度由10 m/s2增加到200 m/s2,摩擦力比值迅速减小;同时,振动钻柱的长度相应增大,钻柱中点的振动速度幅值也相应增加。这是因为随着激振力强度的增加,输入钻柱的能量增加,激振器所在处(即钻柱中点)钻柱获得较大的振动速度,经过衰减后将该振动传递给较远处的钻柱,增加了振动钻柱的长度,当钻柱振动的速度幅值超过钻柱的轴向滑动速度且两者方向相反时,即产生减摩阻作用。
3.1.2 激振力频率
图2为激振频率对摩擦力比值F/F0、振动钻柱长度L和钻柱中点振动速度幅值vm的影响(激振力强度为100 m/s2,摩阻系数为0.4,钻井液黏滞系数为10 s-1)。由图2可以看出,随着激振频率由20 Hz增加到300 Hz,摩擦力比值呈先减小后增加的趋势,振动钻柱长度L和中点振动速度幅值vm均呈先增加后减小的趋势,即摩擦力比值F/F0与振动钻柱长度L和钻柱中点振动速度幅值vm分别具有负相关性。这是因为随着激振频率的增加,当激振频率处于钻柱共振频率附近时钻柱发生共振,使钻柱各点振动速度幅值和振动钻柱长度增加,摩擦力比值减小。

图2 不同激振频率下的振动减摩阻效果Fig.2 Effect of friction reduction by vibration under different excitation frequency
3.1.3 摩阻系数
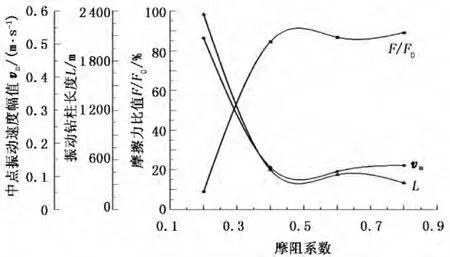
图3 不同摩阻系数下的振动减摩阻效果Fig.3 Effect of friction reduction by vibration under different friction coefficient
图3为计算得到的摩阻系数对摩擦力比值F/F0、振动钻柱长度L和钻柱中点振动速度幅值vm的影响(激振力强度100 m/s2,激振力频率80 Hz,钻井液黏滞系数10 s-1)。从图3可以看出,随着摩阻系数由0.2增加到0.8,F/F0呈先迅速增加而后缓慢增加的趋势,同时,振动钻柱长度L和钻柱中点速度幅值vm均呈与比值F/F0相反的变化趋势。这是因为在较低摩阻系数下钻柱能够有效地振动起来,一旦摩阻系数超过某一临界值,由于钻柱受到过大的阻尼,在一次激励后迅速回到平衡位置,此时再继续增大摩阻系数,其对摩擦力比值、振动钻柱长度和钻柱中点速度幅值的影响将减弱。
3.1.4 钻井液黏滞系数
图4为钻井液黏滞系数对摩擦力比值F/F0、振动钻柱长度L和钻柱中点振动速度幅值vm的影响(激振力强度为100 m/s2,激振频率为80 Hz,摩阻系数为0.4)。从图4可以看出,钻井液黏滞系数由0增加到50 s-1,F/F0由81%增加到94%,振动钻柱的长度由230 m减小到80 m,钻柱中点最大振动速度幅值由0.13 m/s减小到0.065 m/s。这是因为随着钻井液黏滞系数的增加,钻井液的阻尼作用增强,更多的激振能量消耗在克服钻井液黏滞阻力上,使钻柱中点振动速度幅值降低,振动钻柱长度降低,最终摩擦力比值F/F0增加,振动减阻效果变差。
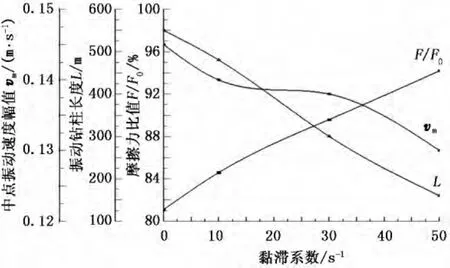
图4 不同钻井液黏滞系数下的振动减摩阻效果Fig.4 Effect of friction reduction by vibration under different drilling fluid viscosity
3.2 正交试验
为了进一步分析激振力强度、激振频率、动摩阻系数和黏滞系数4个因素在不同组合下的振动减摩阻效果及交互作用,采用统计学中的正交试验法,选用L16(45)正交表进行数值试验[12],结果见表1。
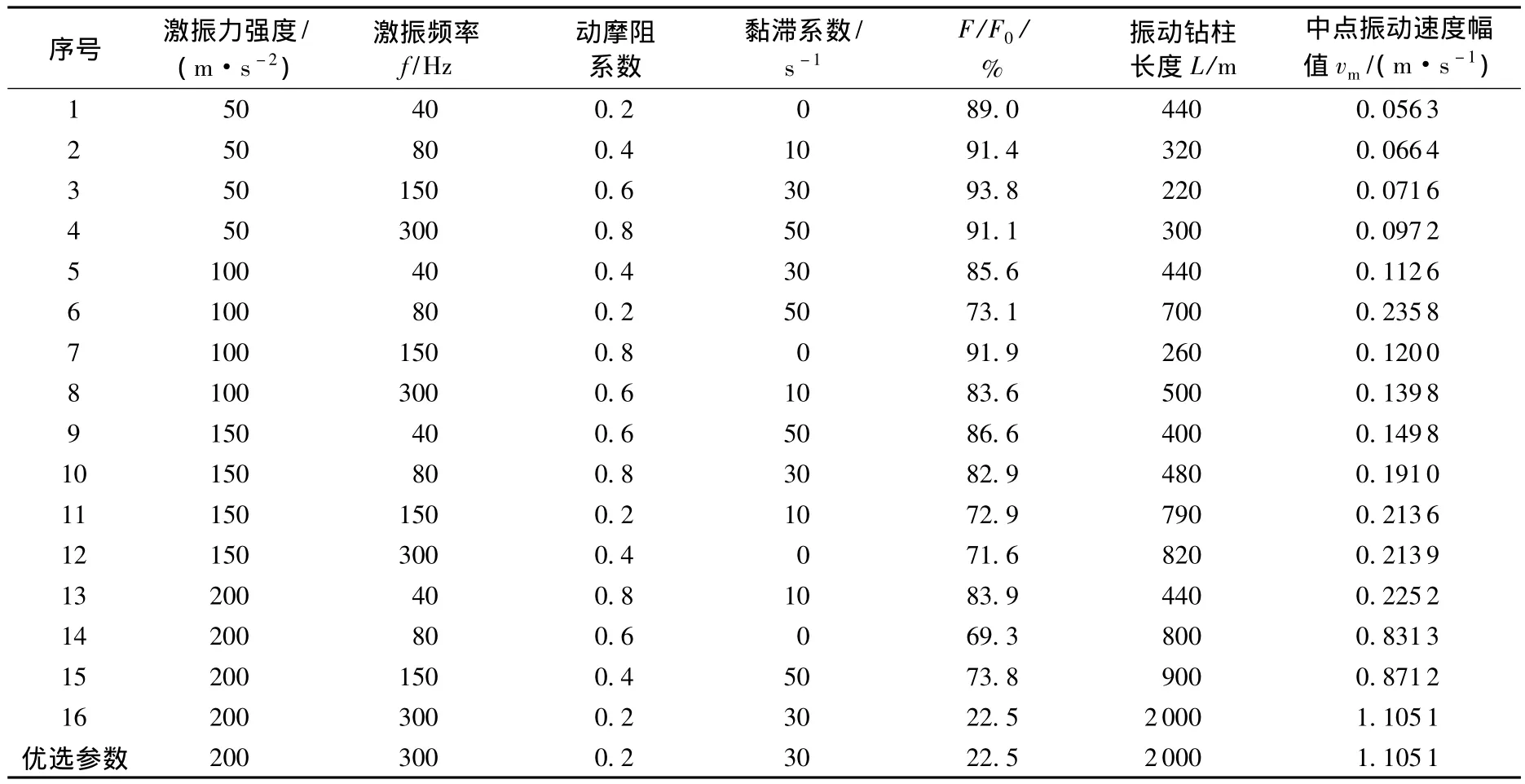
表1 振动减阻参数优选正交试验结果Table 1 Cross experimental results of parameter optimization of friction reduction by vibration
对表1中的正交试验设计结果进行分析,分别以摩擦力比值F/F0、振动钻柱长度L和中点振动速度幅值vm作为考察指标,发现所获得的最优参数组合是一致的(即表1中的优选参数组合),结果进一步验证了减阻效率F/F0与振动钻柱长度L和钻柱中点振动速度幅值vm的相关性。同时,对表1中的正交试验结果进行极差和方差分析,得到各因素的影响作用依次为:激振力强度>摩阻系数>激振频率>钻井液黏滞系数。
研究发现,与钻井工况参数相比,激振工具参数对振动减摩阻效果的影响占主要地位。因此,应优先选用振动减摩阻技术,同时配合使用优化钻井工况参数的措施(如优化井眼轨迹和井身结构、改善钻井液性能等),可获得更加显著的减摩阻效果。
4 结论
(1)振动减小摩阻的机制是振动改变一个振动周期内部分时间段内的瞬时摩擦力方向,使钻柱受到的摩擦力方向与其宏观运动方向相同,此时该摩擦力有助于推动钻柱下行。
(2)振动钻柱长度和钻柱中点振动速度幅值与摩擦力比值一起作为评价振动减摩阻效果的参数,且二者均与摩擦力比值呈负相关性。
(3)通过增大激振力强度和激振频率、降低摩阻系数或钻井液黏滞系数均可降低摩擦力比值,且各因素按照影响程度排序为:激振力强度>摩阻系数>激振频率>钻井液黏滞系数。
[1] 苏义脑,窦修容.大位移井钻井概况、工艺难点和对工具仪器的要求[J].石油钻采工艺,2006,28(2):14-16.SU Yinao,DOU Xiurong.The general situation,process difficulties and requirements for tools of extended well[J].Oil Drilling and Production Technology,2006,28(2):14-16.
[2] ROPER W F,DELLINGER T B,DUNCANVILLE,et al.Reduction of the frictional coefficient in a borehole by the use of vibration:US,4384625[P].1983-05-24.
[3] SKYLES L P,AMIRASLANI Y A,WILHOIT J E.Converting static friction to kinetic friction to drill further and faster in directional holes[R].SPE 151221,2012.
[4] NEWMAN K,BURNETT T,PURSELL J.Modeling the affect of a downhole vibrator[R].SPE 121752,2009.
[5] NEWMAN K R.Vibration and rotation considerations in extending coiled-tubing reach[R].SPE 106979,2007.
[6] 石崇东,党克军,张军,等.水力振荡器在苏36-8-18H井的应用[J].石油机械,2012,40(3):35-38.SHI Chongdong,DANG Kejun,ZHANG Jun,et al.Application of hydraulic oscillator in Su-36-8-18H well[J].China Petroleum Machinery,2012,40(3):35-38.
[7] 刘清友,马德坤,汤小文.钻柱纵向振动模型的建立及求解方法[J].西南石油学院学报,1998,20(4):55-57.LIU Qingyou,MA Dekun,TANG Xiaowen.The model and solving method of drill string longitudinal vibration[J].Journal of Southwest Petroleum Institute,1998,20(4):55-57.
[8] 练章华,李文魁,陈小榆.顶部水泥脉冲振动的数学模型[J].石油学报,2001,22(1):83-87.LIAN Zhanghua,LI Wenkui,CHEN Xiaoyu.Mathematical model of top cement pulse vibration[J].Acta Petrolei Sinica,2001,22(1):83-87.
[9] LITTMANN S W,WALLASCHEK J,MRACEK M.The effect of friction reduction in presence of ultrasonic vibrations and its relevance to travelling wave ultrasonic motors[J].Ultrasonics,2002,40:379-383.
[10] KUMAR V C,HUTCHINGS I M.Reduction of the sliding friction of metals by the application of longitudinal or transverse ultrasonic vibration[J].Tribology Internaltional,2004,37:833-840.
[11] 苏煜城.偏微分方程数值解法[M].北京:气象出版社,1989.
[12] 茆诗松,周纪芗,陈颖.实验设计[M].北京:中国统计出版社,2004.

