用并矢Green函数的矢量本征函数展开式评价金属心轴对多分量感应测井响应的影响
俞燕明,肖加奇,魏宝君,赵彦伟
(1.中石油长城钻探工程有限公司测井技术研究院,北京 102206;2.中国石油大学理学院,山东青岛 266580)
用并矢Green函数的矢量本征函数展开式评价金属心轴对多分量感应测井响应的影响
俞燕明1,肖加奇1,魏宝君2,赵彦伟1
(1.中石油长城钻探工程有限公司测井技术研究院,北京 102206;2.中国石油大学理学院,山东青岛 266580)
基于圆柱坐标系下径向成层介质中并矢Green函数的矢量本征函数展开式分析金属心轴对多分量感应测井响应的影响。为提高计算精度,考虑各分量线圈系的具体形状。将金属心轴作为一层介质处理,既可以考虑其电导率有限、也可以考虑其电导率为无穷大的情况。计算结果表明,金属心轴的存在导致各分量感应电动势实部信号和虚部信号的强度变小。当心轴电导率较小时无论是实部信号还是虚部信号均不随心轴电导率的增加而明显改变。当心轴电导率增加到一定临界值时感应电动势的实部信号快速减小并逐渐稳定到一个较低数值,而虚部信号先逐渐增加再快速减小并逐渐稳定到一个较低数值。
多分量感应测井;金属心轴;并矢Green函数;矢量本征函数
多分量感应测井仪器[1-5]由多组沿三个方向彼此垂直的发射-接收线圈阵列组成,可同时探测各向异性地层如砂-泥岩薄交互层的水平电阻率和垂向电阻率信息,对复杂地层尤其是倾斜井或水平井情况下各向异性地层的高精度对比评价具有重要意义。对于多分量感应测井仪器在复杂地层中响应的模拟,已有很多文献进行了分析讨论[6-11],但这些数值模拟对仪器结构考虑的较为简单,一般将各分量的线圈系作为磁偶极子处理。在多分量感应测井仪器的设计制造过程中,为增加仪器的机械强度,在仪器中心一般置有金属心轴。由于金属心轴电导率较高,各分量发射线圈的电流在其表面产生涡流,金属心轴的涡流与发射线圈的电流共同在接收线圈处产生感应电动势,从而对接收线圈处的电磁信号产生影响。因而有必要分析金属心轴对多分量感应测井响应的影响,并在数值模拟中考虑线圈系的具体结构,从而为实际仪器的刻度提供准确的刻度值。文献[12-13]讨论了金属心轴对仅含轴向线圈系的阵列感应测井仪器响应的影响。笔者基于圆柱坐标系下径向成层介质中并矢Green函数的矢量本征函数展开式讨论金属心轴对多分量感应测井仪器不同分量线圈系响应的影响规律,计算考虑金属心轴和线圈系形状时各分量感应电动势随地层电导率变化的规律。
1 基本理论
由于多分量感应测井仪器心轴的基本形状为圆柱形,并考虑到地层呈轴对称分布,故采用圆柱坐标系。设发射源随时间的变化关系为exp(-iωt),其中ω为角频率,并假设场点位置坐标为R(r,φ,z)、源点位置坐标为R′(r′,φ′,z′)。
1.1 均匀介质中并矢Green函数的矢量本征函数展开式
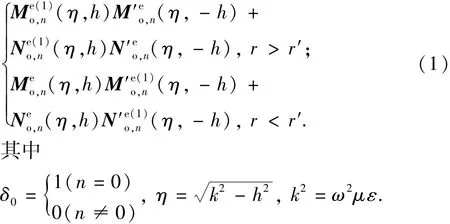
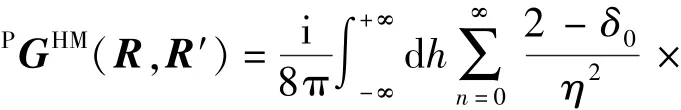


均匀介质中电流源电型并矢Green函数PGEJ(R,R′)的矢量本征函数展开式同PGHM(R,R′),电流源磁型并矢Green函数PGHJ(R,R′)的矢量本征函数展开式同-PGEM(R,R′)。
1.2 径向成2层介质中并矢Green函数的矢量本征函数展开式
考虑到实际需要,首先假设圆柱形径向成层介质由内向外在径向共有2层(图1),层界面半径为r1,每层介质的参数为2μlεl,ηl=(l=1,2)。考虑到多分量感应测井仪器的发射线圈和接收线圈均在心轴外侧,只列出源点位置在第2层,场点位置在不同地层时磁流源和电流源并矢Green函数的矢量本征函数展开式。
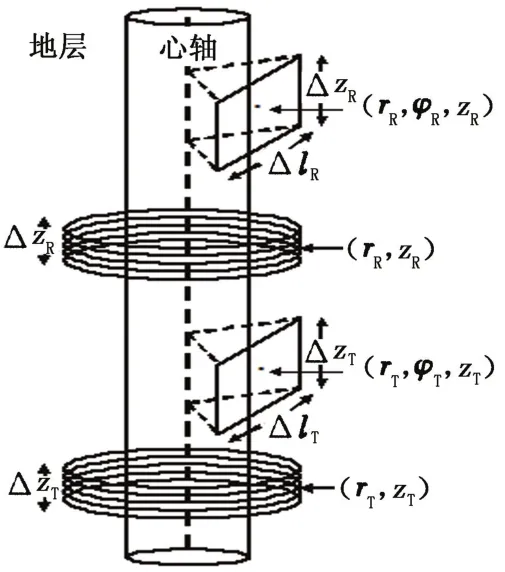
图1 线圈系模型简图Fig.1 Schematic configuration of coils
当场点位置在第1层时:
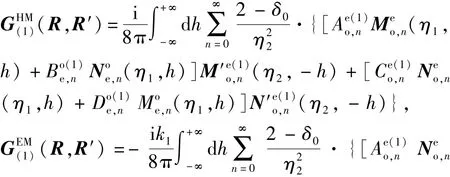

式中,、、为待定系数。
当场点位置在第2层时:
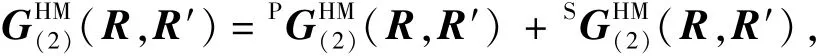
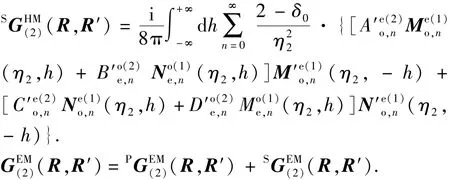

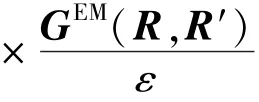
若将金属心轴视为理想导体,其电导率为无穷大,则电磁场只存在于介质2中,对磁流源并矢Green函数而言,圆柱界面r1处^er×(R,R′)=0,则
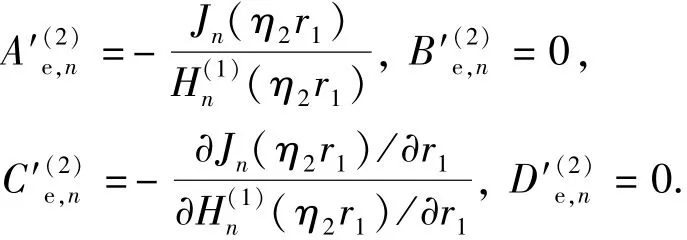
对电流源并矢Green函数而言,圆柱界面r1处(R,R′)=0,则
无论是金属心轴的电导率有限还是无穷大,各待定系数满足如下关系:
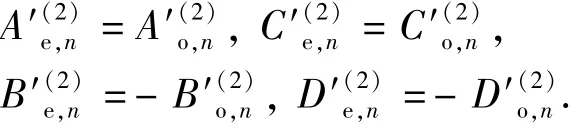
1.3 多分量感应测井响应的计算
多分量感应测井仪器的z向线圈可视为圆柱面,x、y方向的线圈可视为长方形(图1),因而在计算多分量感应测井响应时可分4种情况。
1.3.1z向发射、z向接收(即zz分量)
设发射线圈半径为rT,中心点轴向坐标为zT,匝数为NT,电流强度为IT,接收线圈半径为rR,中心点轴向坐标为zR,匝数为NR。发射线圈沿轴向均匀排列在轴向宽度为ΔzT的圆柱面上,接收线圈沿轴向均匀排列在轴向宽度为ΔzR的圆柱面上,则发射线圈上的电流密度可表示为

而地层中的电磁场强度可表示为

式中,D为电流源所在的区域。将式(3)代入式(4),得
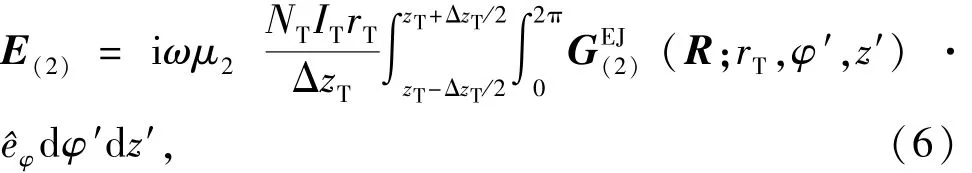
接收线圈处的感应电动势可表示为
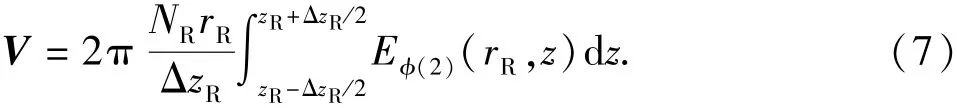
将式(6)代入式(7),得
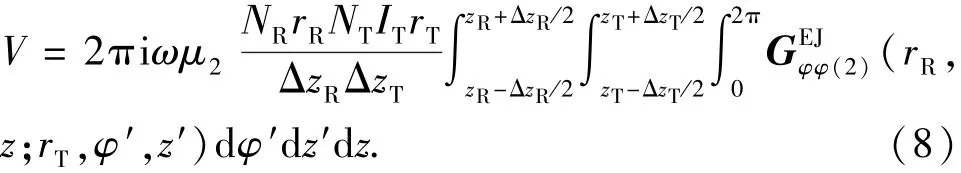
根据并矢Green函数的展开特点,式(8)的各项积分均可以通过解析方式得到,且并矢Green函数只含有n=0阶项。
1.3.2z向发射、x或y向接收(即zx分量或zy分量)
设接收线圈中心点坐标为(rR,φR,zR)、高度为ΔzR、宽度为ΔlR,在垂向坐标为z、局部横向位置为l处取一高度为dz、宽度为dl的长方形面元ds,则该面元在圆柱坐标系下的坐标为
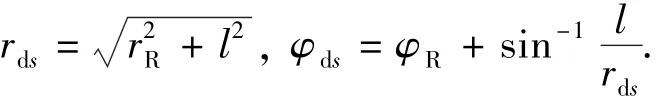
该小面元处的总磁通为
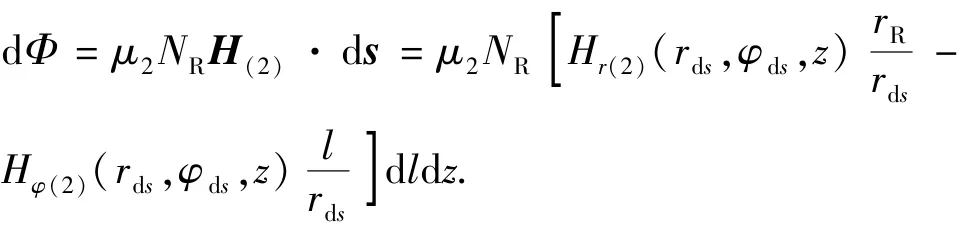
接收线圈的感应电动势为
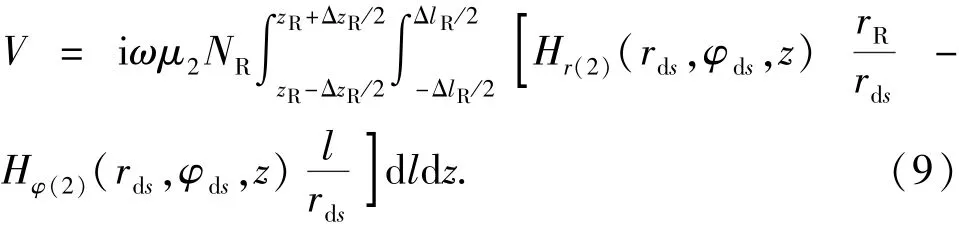
式(9)中的磁场强度可通过将式(3)代入式(5)得到,即
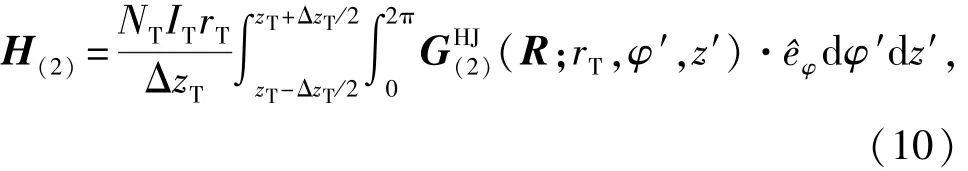
由于发射线圈产生的磁场没有φ分量,将式(10)代入式(9)得
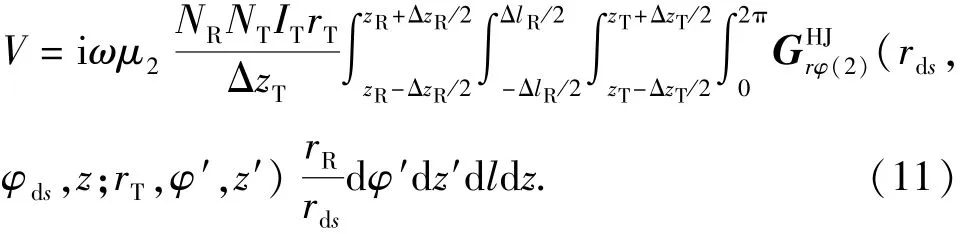
式中除第三重对dl的积分需用数值计算外,其他积分均可以通过解析方式得到,且并矢Green函数只含有n=0阶项。
1.3.3x或y向发射、z向接收(即xz分量或yz分量)
设发射线圈中心点坐标为(rT,φT,zT)、高度为ΔzT、宽度为ΔlT,在垂向坐标为z′、局部横向位置为l′处取一高度为dz′、宽度为dl′的长方形面元ds′,则该面元在圆柱坐标系下的坐标为

该面元所绕线圈的磁偶极矩可表示为
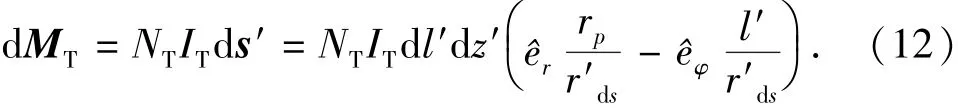
而地层中的电磁场强度可表示为
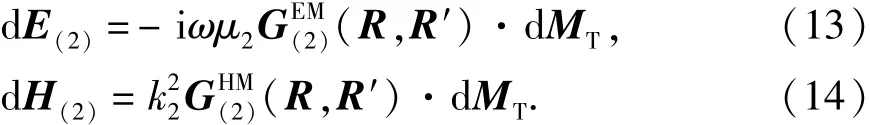
结合式(12)~(14),得到长方形发射线圈在地层中产生的电磁场强度为
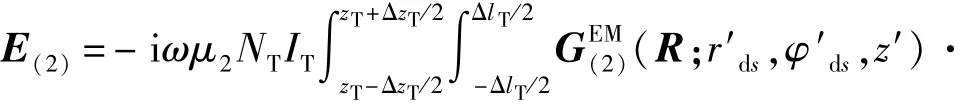

接收线圈处的感应电动势可表示为

将式(15)代入式(17),得
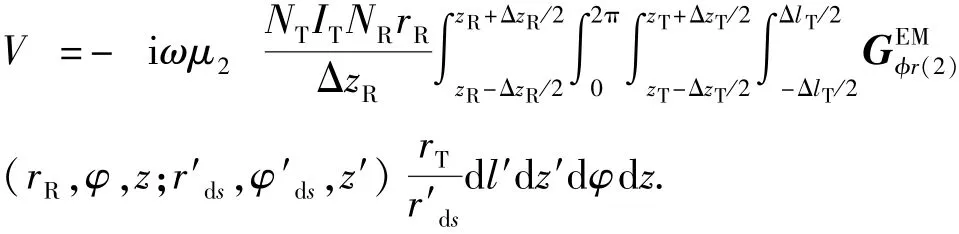
式中除第一重对dl′的积分需用数值计算外,其他积分均可以通过解析方式得到,且并矢Green函数只含有n=0阶项。
1.3.4x或y向发射、x或y向接收(即xx、xy、yx或yy分量)
将式(16)代入式(9),得
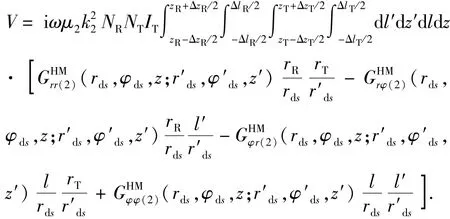
式中,第二重和第四重对dz′、dz的积分可解析得到,第一重和第三重对dl′、dl的积分需用数值计算。
2 数值算例
2.1 多分量感应测井响应与均质地层电导率的关系
假设发射线圈电流IT=1 A、金属心轴半径r1= 0.0127 m,分别考察心轴电导率σ1为0和无穷大时各分量感应电动势随均质地层电导率σ2的变化关系。
2.1.1zz分量的感应电动势
z向发射线圈由两部分组成,匝数NT=50、半径rT=0.033 m、轴向宽度ΔzT=0.052 m、中心点轴向坐标分别为zT=±0.0565 m。z向接收线圈由主接收线圈和屏蔽接收线圈两部分组成,rR=rT。主接收线圈匝数NR=90、中心点轴向坐标zR=1.143 m、轴向宽度ΔzR=0.09434 m,屏蔽接收线圈匝数N′R=-40、中心点轴向坐标z′R=0.8737 m、轴向宽度Δz′R=0.04134 m。取发射频率为44 kHz。图2给出了zz分量感应电动势随均质地层电导率变化关系。该分量亦采用文献[18]的方法进行了模拟计算,两种方法的计算结果完全一致,说明了本文方法的正确性。
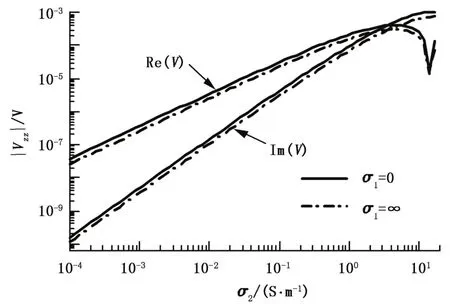
图2zz分量感应电动势随均质地层电导率变化关系Fig.2 Relationship betweenzz-component's electromotive force and homogeneous formation's conductivity
2.1.2zx分量的感应电动势
所采用频率和z向发射线圈参数同上。x向接收线圈系的高度ΔzR=0.036 m、宽度ΔlR=0.04326 m、中心点径向坐标rR=0.02725 m。接收线圈系由方位角分别在φR=0°和φR=180°的两对完全相同的主接收/屏蔽接收线圈组成。主接收线圈匝数NR=44、中心点轴向坐标zR=1.6 m,屏蔽接收线圈匝数N′R=-22、中心点轴向坐标z′R=1.27 m。图3给出了zx分量感应电动势随均质地层电导率变化关系。
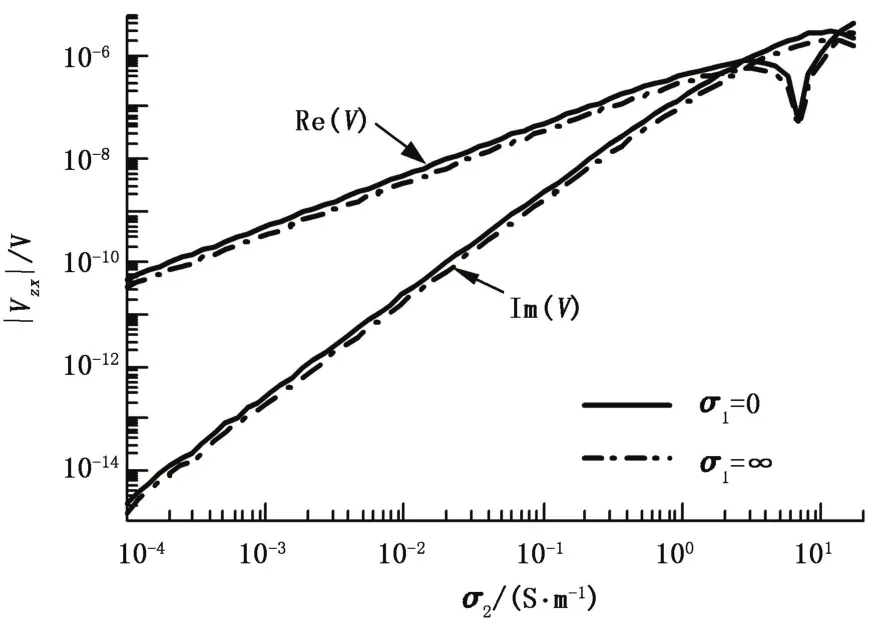
图3zx分量感应电动势随均质地层电导率变化关系Fig.3 Relationship betweenzx-component's electromotive force and homogeneous formation's conductivity
2.1.3xz分量的感应电动势
取发射频率为64 kHz,z向接收线圈参数同上。x向发射线圈系由方位角分别在φT=0°和φT=180°处完全相同的两个线圈组成,匝数NT=39、中心点轴向坐标zT=0.0 m、中心点径向坐标rT=0.02725 m、高度ΔzT=0.036 m、宽度ΔlT=0.04326 m。图4给出了xz分量感应电动势随均质地层电导率变化关系。

图4xz分量感应电动势随均质地层电导率变化关系Fig.4 Relationship betweenxz-component's electromotive force and homogeneous formation's conductivity
2.1.4xx分量的感应电动势
取发射频率为64 kHz,x向发射线圈系和x向接收线圈系结构及参数同上。图5给出了xx分量感应电动势随均质地层电导率变化关系。
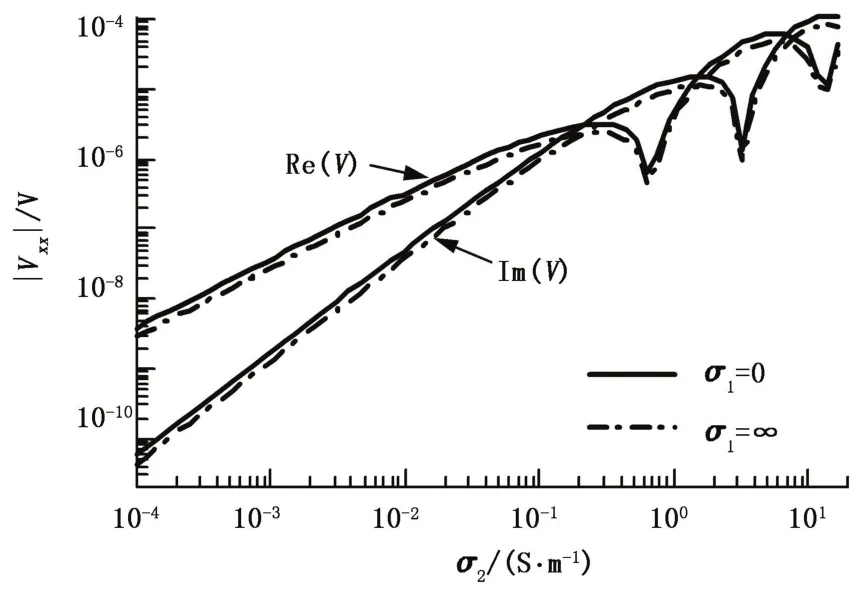
图5xx分量感应电动势随均质地层电导率变化关系Fig.5 Relationship betweenxx-component's electromotive force and homogeneous formation's conductivity
由图2~5可以看出,由于金属心轴的存在使发射线圈和接收线圈的有效面积减小,故各分量感应电动势实部和虚部的绝对值亦相应减小,且不同分量感应电动势减小的规律相同。当然,不同线圈距、不同分量感应电动势的数值及其随均质地层电导率的变化关系是有差别的。计算发现,对同一分量而言,线圈距越大,信号强度越小,并且在电导率越小时感应电动势开始出现震荡,说明对地层电导率的探测范围变小。对比不同分量的感应电动势发现,xx分量对地层电导率的探测范围最小。由于已考虑到各分量线圈系的具体形状和金属心轴的影响,该仪器模型更接近于实际仪器的结构,因而图2~5的模拟数据更接近于仪器测量值,从而可为实际仪器提供更高精度的刻度值。
2.2 多分量感应测井响应与钻井液电导率的关系
在存在井眼的情况下,采用径向成3层介质模型,第1层介质为金属心轴、第2层介质为井眼、第3层介质为原状均质地层。设井眼半径r2=0.12 m、原状地层电导率σ3=0.2 S·m-1,线圈系参数同上。图6给出了部分分量的感应电动势随井眼内钻井液电导率σm的变化关系。由图6可以得到相同结论,即在存在井眼的情况下各分量感应电动势实部和虚部的绝对值均相应减小。
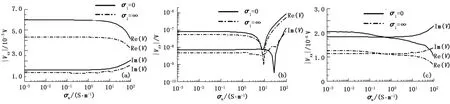
图6 不同分量感应电动势随钻井液电导率变化关系Fig.6 Relationship between different component's electromotive force and drilling mud's conductivity
2.3 多分量感应测井响应与心轴电导率的关系
为了考察心轴电导率的不同取值对各分量感应电动势的影响,固定均质地层电导率σ2=0.2 S· m-1,取发射频率分别为44和68 kHz。图7给出了zz分量接收线圈系的感应电动势随心轴电导率的变化关系。图8给出了zx分量接收线圈系的感应电动势随心轴电导率的变化关系。对其他分量可得到相似规律。

图7zz分量感应电动势随心轴电导率变化关系Fig.7 Relationship betweenzz-component's electromotive force and mandrel's conductivity
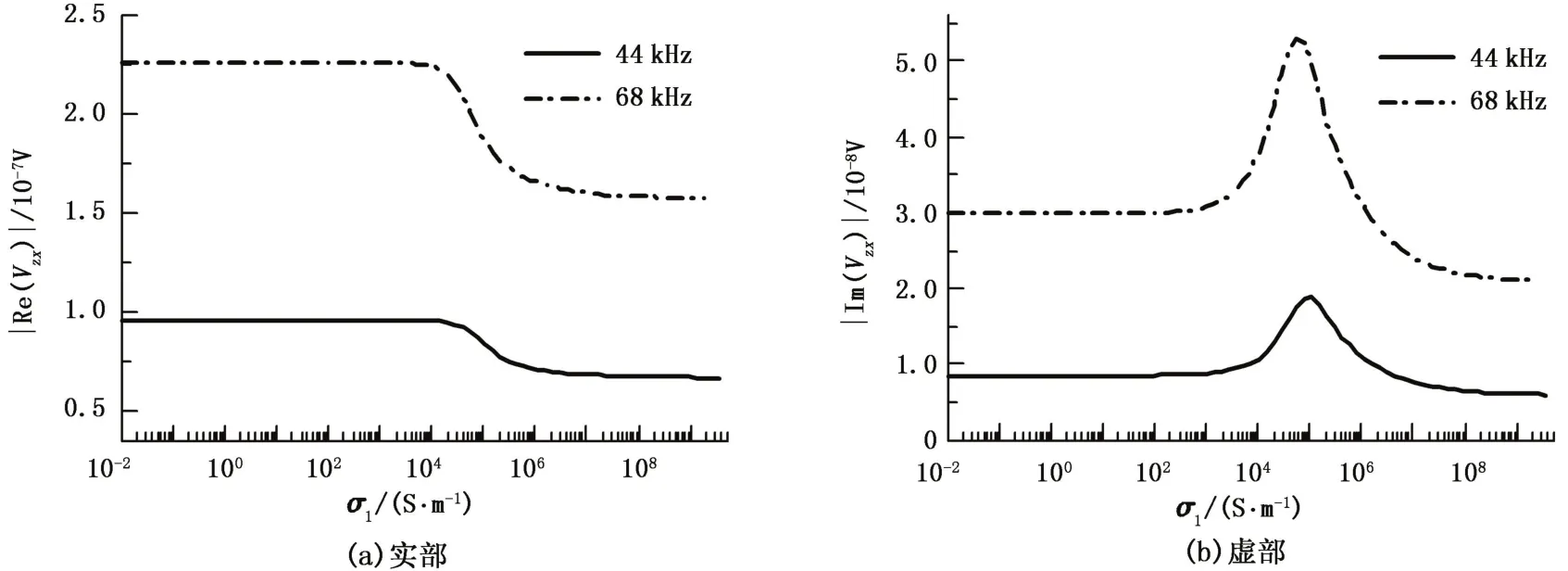
图8zx分量感应电动势随心轴电导率变化关系Fig.8 Relationship betweenzx-component's electromotive force and mandrel's conductivity
由图7~8可以看出,各分量实部感应电动势与虚部感应电动势随心轴电导率的变化关系是不同的。对各分量实部感应电动势而言,当心轴电导率较小时其数值并不随心轴电导率的增加而明显改变,只有当心轴电导率增加到一定临界值时感应电动势数值快速减小,此后逐渐稳定到一个较低数值。对各分量虚部感应电动势而言,当心轴电导率较小时其数值亦不随心轴电导率的增加而明显改变,当心轴电导率增加到一定临界值时感应电动势数值先逐渐增加再快速减小,此后逐渐稳定到一个较低数值。心轴电导率的临界值与频率有关,频率越高,心轴电导率的临界值越小。
3 结 论
(1)采用基于圆柱坐标系下径向成层介质并矢Green函数的矢量本征函数展开式可有效模拟含金属心轴多分量感应测井仪器在径向成层地层中的响应。由于在模拟中考虑了金属心轴对仪器响应的影响,不仅能为多分量感应测井刻度装置设计提供理论依据,而且能用于高精度的刻度器地层等效读数的计算。
(2)当金属心轴存在时,多分量感应测井仪器各分量感应电动势实部信号和虚部信号的强度变小,且不同分量感应电动势减小的规律相同。
(3)各分量感应电动势的实部信号和虚部信号随心轴电导率的变化关系不同。当心轴电导率较小时无论是实部信号还是虚部信号均不随心轴电导率的增加而明显改变。当心轴电导率增加到一定临界值时,感应电动势的实部信号快速减小,并逐渐稳定到一个较低数值,而虚部信号先逐渐增加再快速减小,并逐渐稳定到一个较低数值。
[1] KRIEGSHAUSER B,FANINI O,FORGANG S,et al.A new multi-component induction logging tool to resolve anisotropic formations[C/CD].SPWLA 41st Annual Logging Symposium,2000,paper D.
[2] KRIEGSHAUSER B,FANINI O,YU L,et al.Improved shaly sand interpretation in highly deviated and horizontal wells using multicomponent induction log data[C/CD]. SPWLA 42nd Annual Logging Symposium,2001,paper S.
[3] ZHDANOV M,KENNEDY D,PEKSEN E.Foundations of tensor induction well-logging[J].Petrophysics,2001, 42(6):588-610.
[4] ZHANG Z,YU L,KRIEGSHAUSER B,et al.Simultaneous determination of relative angles and anisotropic resistivity using multicomponent induction logging data[C/ CD].SPWLA 42nd Annual Logging Symposium,2001, paper Q.
[5] MALLAN R K,TORRES-VERDIN C.Effects of petrophysical,environmental,and geometrical parameters on multi-component induction measurements acquired in high-angle wells[C/CD].SPWLA 47th Annual Logging Symposium,2006,paper PPP.
[6] 汪功礼,张庚骥,崔锋修,等.三维感应测井响应计算的交错网格有限差分法[J].地球物理学报,2003, 46(4):561-567.
WANG Gongli,ZHANG Gengji,CUI Fengxiu,et al. Application of staggered grid finite difference method to the computation of 3-D induction logging response[J]. Chinese Journal of Geophysics,2003,46(4):561-567.
[7] 王昌学,杨韦,储昭坦,等.多分量感应测井响应的交错网格有限差分法模拟[J].石油大学学报:自然科学版,2005,29(3):35-40.
WANG Changxue,YANG Wei,CHU Zhaotan,et al. Modeling of multicomponent induction logging response by staggered grid finite difference method[J].Journal of the University of Petroleum,China(Edition of Natural Science),2005,29(3):35-40.
[8] WANG H N,SO P,YANG S W,et al.Numerical modeling of multicomponent induction well-logging tools in the crlindrically stratified anisotropic media[J].IEEE Trans on Geosci and Remote Sensing,2008,46(4):1134-1147.
[9] 汪宏年,陶宏根,姚敬金,等.用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应[J].地球物理学报,2008,51(5):1591-1599.
WANG Hongnian,TAO Honggen,YAO Jingjin,et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method[J].Chinese Journal of Geophysics,2008,51(5):1591-1599.
[10] 魏宝君,王甜甜,王颖.用磁流源并矢Green函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应[J].地球物理学报,2009,52(11):2920-2928.
WEI Baojun,WANG Tiantian,WANG Ying.Computing the response of multi-component induction logging in layered anisotropic formation by the recursive matrix method for magnetic-current-source dyadic Green's function[J].Chinese Journal of Geophysics,2009,52 (11):2920-2928.
[11] 张国艳,肖加奇,肖占山,等.三维感应测井仪器在三维井眼环境中的正演模拟[J].中国石油大学学报:自然科学版,2013,37(3):63-67.
ZHANG Guoyan,XIAO Jiaqi,XIAO Zhanshan,et al. Forward modeling of 3D induction logging tool in 3D borehole environment[J].Journal of China University of Petroleum(Edition of Natural Science),2013,37(3): 63-67.
[12] 魏宝君,张庚骥,张中庆,等.金属心棒对阵列感应测井仪器的影响[J].测井技术,1998,22(4):245-249.
WEI Baojun,ZHANG Gengji,ZHANG Zhongqing,et al.Influence of the metal mandrel on the array induction logging tool[J].Well Logging Technology,1998,22 (4):245-249.
[13] 魏宝君,张庚骥.含金属心棒阵列感应测井仪器的井眼校正[J].石油大学学报:自然科学版,1999,23 (3):22-26.
WEI Baojun,ZHANG Gengji.Borehole correction of array induction logging tool with metal mandrel[J].Journal of the University of Petroleum,China(Edition of Natural Science),1999,23(3):22-26.
[14] 戴振铎,鲁述.电磁理论中的并矢格林函数[M].武汉:武汉大学出版社,1996.
[15] 魏宝君.一种新型随钻电阻率测井仪器的响应和刻度[J].地球物理学报,2007,50(2):632-641.
WEI Baojun.Response and calibration of a new loggingwhile-drilling resistivity tool[J].Chinese Journal of Geophysics,2007,50(2):632-641.
[16] 魏宝君,田坤,张旭,等.用并矢Green函数的矢量本征函数展开式评价偏心对随钻电磁波电阻率测井响应的影响[J].中国石油大学学报:自然科学版, 2010,34(5):57-62.
WEI Baojun,TIAN Kun,ZHANG Xu,et al.Evaluating influence of eccentricity on response of electromagnetic wave resistivity logging-while-drilling by vector eigenfunction expansion formulae for dyadic Green's functions[J].Journal of China University of Petroleum(E-dition of Natural Science),2010,34(5):57-62.
[17] 魏宝君,王莎莎,欧永峰.用并矢Green函数的矢量本征函数展开式模拟随钻感应测井仪器的响应[J].地球物理学报,2011,54(5):1391-1401.
WEI Baojun,WANG Shasha,OU Yongfeng.Simulating the response of induction logging-while-drilling tools by vector eigenfunction expansion formulae for dyadic Green 's functions[J].Chinese Journal of Geophysics,2011, 54(5):1391-1401.
[18] 魏宝君,王颖,王甜甜.电磁波电阻率仪器的基本理论及其在随钻测量中的应用[J].地球物理学进展, 2009,24(2):774-781.
WEI Baojun,WANG Ying,WANG Tiantian.The basic theory of electromagnetic wave resistivity instrument and its application to measurement of while-drilling[J].Progress in Geophysics,2009,24(2):774-781.
(编辑 修荣荣)
Evaluating influence of metal mandrel on response of multi-component induction logging by vector eigenfunction expansion formulae for dyadic Green's functions
YU Yanming1,XIAO Jiaqi1,WEI Baojun2,ZHAO Yanwei1
(1.Logging Technique Research Institute of Great Wall Drilling Company in China National Petroleum Corporation, Beijing 102206,China; 2.College of Science in China University of Petroleum,Qingdao 266580,China)
The influence of metal mandrel on the response of multi-component induction logging was analyzed using the vector eigenfunction expansion formulae for dyadic Green's functions of radial-layered medium in cylindrical coordinate system.The shape of each component's coils was taken into account in order to increase the computational precision.The metal mandrel was assumed as a layer of medium whose conductivity can be both finite and infinite.The results show that the intensity of both the real and imaginary parts of each component's electromotive force will decrease because of the introduction of the metal mandrel.There is no distinct change in both the real and imaginary parts of the electromotive force when the amount of increase of the mandrel's conductivity is small.Both the real and imaginary parts of the electromotive force decrease rapidly when the mandrel's conductivity reaches a critical value,and then the real part will gradually achieve a stable lower value. While the imaginary part will first increase and then decrease when the mandrel's conductivity reaches the critical value,it will also gradually achieve a stable lower value eventually.
multi-component induction logging;metal mandrel;dyadic Green's functions;vector eigenfunction
P 631.9
A
1673-5005(2014)04-0057-08
10.3969/j.issn.1673-5005.2014.04.008
2013-10-05
国家“十二五”重大专项(2011ZX05020-004)
俞燕明(1983-),男,工程师,博士,研究方向为电法测井与核磁共振理论方法。E-mail:yuyanming@cnlc.cn。
俞燕明,肖加奇,魏宝君,等.用并矢Green函数的矢量本征函数展开式评价金属心轴对多分量感应测井响应的影响[J].中国石油大学学报:自然科学版,2014,38(4):57-64.
YU Yanming,XIAO Jiaqi,WEI Baojun,et al.Evaluating influence of metal mandrel on response of multi-component induction logging by vector eigenfunction expansion formulae for dyadic Green's functions[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(4):57-64.

