军队采购中的询价策略探析*
佘 键 李 浩 黄金明
(武警警官学院数理系 成都 610213)
军队采购中的询价策略探析*
佘 键 李 浩 黄金明
(武警警官学院数理系 成都 610213)
军队采购是以最优的质量、最合适的价格、最恰当的时间、最适当的数量,从合格的供应商处获取所需要的物资、工程和服务,保障部队的需要。军队采购方与供应商形成一种买卖博弈或讨价还价博弈。需要设计一种显示机制,让供应商自动显示其生产成本,以达到军队采购经济高效的目的。
军队采购; 询价; 策略; 机制
Class Number D920
1 引言
采购是一种采用适当的交易技术与策略,按照一定的方式及运作程序,以最低的成本,高效地从供应商获取所需数量和质量的物资和劳务的活动。军队采购作为中国人民解放军后勤保障的主要环节之一,是国家经济力转化为后勤保障力和军队战斗力的重要途径。军队采购的目标就是以最优的质量、最合适的价格、最恰当的时间、最适当的数量,从合格的供应商处获取所需要的物资、工程和服务,保障部队的需要。
为表述方便起见,在军队采购中,称采购单位为甲方,供应厂商为乙方。甲方希望用尽可能低的价格在乙方那里购买到自己需要的物资或装备,而乙方则希望以尽可能高的价格出售甲方想要得到的物资或装备。这是一个矛盾,所以,甲乙双方的行为就形成了一个买卖博弈或讨价还价博弈。需要研究解决的问题是:甲方找到或预测出乙方的成本价格。
2 信息结构
整体来讲,买卖双方是一种不对称信息。甲方的私人信息是购买数量;乙方的私人信息是成本价格。第一,这两个信息本身具有“私有性”,问题是甲乙双方为什么保留这种“私有性”而不让其成为公共信息。第二,如果将这两个信息的“私有性”公开而成为共有信息,其结果是:乙方无法利用“成本价格”的私有信息来获取更高的卖价,甲方无法利用“购买数量”的私有信息来获取更低的买价。第三,甲方受制于乙方,是因为乙方将“成本价格”保持私有,才使得甲方也将其“购买数量”也保持为私有。如果甲方的购买数量少,乙方会要求更高的价格;反之,如果甲方的购买数量大,乙方就会愿意降低其价格。
3 机制设计
3.1 理性行为假设
任何一种机制设计,必须对行为人的行为策略做出某种理性假设。甲方要利用其“购买数量”这个私有信息,来设计一种“机制”,能够让乙方自动显示出他的“成本价格”。乙方为什么会自动显示其“成本价格”这个私有信息呢?或者说,乙方自动显示的“成本价格”这个私有信息是真实的吗?对于这个问题,在甲方看来,必须在其设计的“机制”中予以保证。如果乙方按照“理性”行为准则行事,其自动显示“成本价格”就应该是真实的价格。这样就有理性行为假设:乙方按照“利润最大化”原则来实施自己的行为。
3.2 成本价格区间
对于甲方而言,尽管不能确知乙方的成本价格,但是能够知道其大概范围,假设这个成本价格区间为[Pmin,Pmax],也就是说,乙方的成本价格c一定落在这个区间内。对于乙方而言,他不会按成本价格c出售商品,而是以一定的成本加成后的价格出售。同时,甲方也不会苛刻地要求乙方按成本价格出售商品,也愿意给乙方一定的成本加成。
假设甲、乙双方成本加成幅度的最小值为d。求出c的精确值既困难也没必要,只要求出其相对精确的一个范围即可。假设这个精度误差为d。将价格区间[Pmin,Pmax]以d/2等分成n个小区间:
P1=Pmin,P2=P1+d/2,…,Pn=Pmax,
其中Pi+1-Pi=d/2(i=1,2,…,n-1)。
3.3 机制设计-成本价格显示模型
3.3.1 显示原理
甲方向乙方开出如下n个购买契约:
(P1,Q1),(P2,Q2),…,(Pn,Qn),
让乙方从中选择一个契约执行。其中,(Pi,Qi)表示甲方以Pi的价格购买数量为Qi的商品。这里,Pi是已知的,为上述价格区间的分割点;Qi是甲方需要确定的购买数量。
甲方希望能够从乙方的选择中确知乙方的成本价格c。如果乙方的选择是(Pi,Qi),那么乙方的成本价格c肯定小于Pi。如果c比Pi小得太多,那么对甲方是不利的。所以甲方希望乙方的报价Pi是接近于其成本价格c的。只有当乙方的报价Pi与其成本价格c比较接近时,乙方能获得最大的利润,乙方才有积极性这样做。此时,乙方的利润是:(Pi-c)Qi,而且(Pi-c)Qi≥(Pj-c)Qj(∀j≠i)。这里Pi是已知的分割点,甲能够控制的是其购买的数量Qi。如果甲方能够选择适当的购买数量Qi使上述不等式成立,那么甲方就成功地实现了自己的目的。
3.3.2 显示机制设计
当P1 (P3-c)Q3≥(Pi-c)Qi(∀i≠2,3) 显然,当i=1时,P1 所以,当Q3≥(i-1)Qi(∀i≥4),就能保证: (P3-c)Q3≥(Pj-c)Qj(∀j=4,5,…,n) 一般地,如果乙方的成本价格c满足Pk-2 (Pk-c)Qk≥(Pi-c)Qi(∀i≠k-1,k) 显然,当i≤k-2时,Pi (∀i≥k+1) 所以当Qk≥(i-k+2)Qi(∀i≥k+1)时,就能保证 (Pk-c)Qk≥(Pi-c)Qi(∀i≠k-1,k) 总结:对于任意给定的k=3,4,…,n,甲方的购买数量Qk满足: Qk≥(i-k+2)Qi(∀i≥k+1) 如果乙方的成本价格c∈(Pk-2,Pk-1],那么乙方利润最大的卖价为Pk-1或Pk。换句话说,假设乙方是追求利润最大化的理性行为人,如果乙方选择契约(Pk,Qk),那么乙方成本价格c就位于Pk-2到Pk-1之间。此时,甲方就成功探测出了乙方的成本价格范围。 在上述显示机制设计部分,为了显示乙方的成本价格,确定了甲方在不同价格条件下购买数量要满足的条件: Qk≥(i-k+2)Qi(∀i≥k+1,k=3,4,…,n) 那么,一个自然的问题是:这些不等式是否存在可行解?通过简单分析可知,当Qi=2n-i,上述不等式成立。这组Qi表示随着购买价格的增高,购买数量以指数下降方式减少。 也可以选择其它形式。这样,我们就得到了如下形式的显示乙方成本价格的二次规划模型: s.t.Qk≥λ(i-k+2)Qi(∀i,k;i≥k+1) 求解此模型得到Q1,Q2,…,Qn的一组值,从而就确定了甲方的一组契约:(P1,Q1),(P2,Q2),…,(Pn,Qn)。如果乙方在这组契约中选择(Pk,Qk),说明乙方的成本价格处于区间[Pk-2,Pk)之内。如果赋予甲方可以修改一次购买数量的权力,此时甲方可以请求将契约(Pk,Qk)修改为(Pk,S)。这里,甲方没有改变乙方的销售价格,而只是改变了自己的购买数量,乙方似乎难以拒绝这一点。至少甲方获知了乙方的成本价格不会大于Pk。甲乙双方在签订购销合同时,可以约定甲方有一次修改购置数量的权力,而没有修改订购价格的权力。在甲方看来,如果乙方要价过高,甲方有权减少采购数量,如果乙方要价适当,甲方也可以增加采购数量,这是一个合理的要求。 [1] 万毅.军队采购学[M].北京:解放军出版社,2004:55-68. [2] 谢识予.经济博弈论[M].上海:复旦大学出版社,2010:130-142. [3] 孙兆斌.武器装备采购中的博弈分析[J].军事经济研究,2010(11):12-15. [4] 黄河.多物品组合采购两阶段机制设计[J].系统工程学报,2011(2):35-40. [5] 周建鹏.低碳经济背景下企业生产策略的演化博弈分析[J].科技进步与对策,2011(12):23-25. [6] 汪定伟.网上集中采购的捆绑-组合拍卖机制设计[J].系统工程学报,2011(12):10-15. [7] 谷飙.博弈论机制设计的方法论意义[J].天津商业大学学报,2012(4):22-25. [8] 刘白羽,黄金元.基于机制设计理论的装备采办系统设计研究[J].科技广场,2009(9):41-44. [9] 魏刚著.武器装备采办合同理论研究与实证分析[M].北京:国防大学出版社,2003:35-56. [10] 翟羽佳,李帮义,李菁.基于博弈分析的供应链质量协调机制设计[J].价值工程,2010(11):23-24. The Strategy of Making Inquiries in Military Procurement SHE Jian LI Hao HUANG Jinming (Department of Mathematics & Physics, Officers College of CAPF, Chengdu 610213) Military procurement is about obtaining needed materials, engineering and services from qualified suppliers with the most optimal quality, best price, the most appropriate time and the most appropriate numbers to guarantee the needs of the forces. Army purchaser and supplier form a game to bargain. In order to achieve the goal of military procurement efficiency, the purchaser should design a mechanism to make the supplier display the production cost automatically. military procurement, inquiry, strategy, mechanism 2014年6月20日, 2014年8月3日 佘键,男,硕士,助教,研究方向:军事运筹学。李浩,男,硕士,讲师,研究方向:军事运筹学。黄金明,男,副教授,硕士生导师,研究方向:军事运筹学 D920 10.3969/j.issn1672-9730.2014.12.032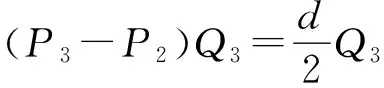
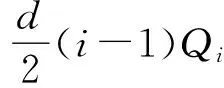
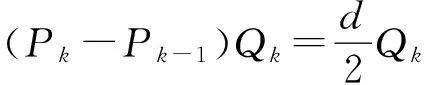
4 结论与展望