结构动力弹塑性和倒塌分析(III)*——地震差动作用下输电塔—线体系的弹塑性与倒塌分析
柳国环,练继建,孙雪艳,国 巍
(1.天津大学建筑工程学院,天津300072;2.天津大学水利工程仿真与安全国家重点实验室,天津300072;3.北京金土木软件技术有限公司,北京100048;4.中南大学土木工程学院,湖南长沙410075)
0 前言
《结构动力弹塑性与倒塌分析(Ⅰ)》作为该系列工作的第I部分,开发了可链接ABAQUS主程序的显式与隐式方法子程序,并从材料和构件层面分别验证了子程序的可靠性(柳国环等,2014a)。《结构动力弹塑性与倒塌分析(Ⅱ)作为该系列工作的第II部分,开发了SAP2ABAQUS可视化导航式界面的接口程序,给出了使用注记,并通过几类典型结构模型验证了采用SAP2ABAQUS转化过程的可行性和转化结果的准确性(柳国环等,2014b)。
本文作为该系列工作的第III部分,将上述第I和II两部分内容结合起来应用于主塔高375 m,主跨2 756 m的大跨越输电塔—线体系在多点地震动作用下的地震弹塑性和倒塌反应分析。结构体系构件包括角钢、钢管、钢管混凝土、拉索等较为多样丰富构件形式,具有代表性。区别于以往大多对输电塔线体系地震反应的材料弹性分析,本文重点从工程实际角度进一步检验第I和II部分内容所开发程序的现实性和可靠性,同时分析该结构体系在超大震和多点地震动输入作用下的薄弱环节、弹塑性和倒塌模式。
本文具体内容包括:(1)采用《结构动力弹塑性与倒塌分析(Ⅱ)》中SAP2ABAQUS对该工程进行模型转化,对转化前后模型中的构件细节与模态结果进行对比,进一步从实际工程层面检验SAP2ABAQUS接口程序的转化精度;(2)采用《结构动力弹塑性与倒塌分析(Ⅰ)》中子程序并链接到ABAQUS主程序计算结构体系的反应,可为工程实际提供有效依据,并从工程实际层面进一步检验所开发子程序的现实可靠性;(3)给出采用长周期动力加载法实现静力重力加载过程,理论严格合理、现实可行,克服了General/static的重力加载方式与Explicit/dynamic分析工况不续接问题;(4)从模态与结构反应两方面考察边界条件对结构体系动力特性尤其是对结构体系薄弱环节和倒塌模式的影响,并根据计算结果分析得到可用于指导工程的意义性建议;(5)对比分析地震动输入模式(一致与多点激励)对结构反应,尤其是对结构体系薄弱环节、影响区域以及随后倒塌的影响,进而强调多点地震动输入对于此类结构体系倒塌模式影响的敏感性。
1 模型与研究对象
1.1 工程概况
浙江舟山大跨越输电塔—线体系主塔高375 m、档距2 756 m、导线(索)长2 900 m,高度与跨度分别居世界和亚洲之最。两主塔分别坐落于大猫山和凉帽山,边塔与主塔间由悬链线型导线索链接。该结构体系是由大陆向舟山地区输送电量的主要载体,在地震作用下安全运行以正常发挥其输送电量的功能需要得以保障。结构体系中主要构件形式为:圆钢管、角钢、圆钢管混凝土与导/地线。
1.2 有限元模型的建立、验证与选取
首先建立如图1所示的SAP有限元模型,构件和导线分别采用梁单元和索单元模拟,共有3 332个梁单元与1 800个索单元。模型中钢材型号主要为 Q340,部分为钢管混凝土采用 C50,索(导线与地线)的密度分别为1 231 kg/m3和5 607 kg/m3。采用SAP2ABAQUS转化后相应的有限元模型如图2所示。从图中整体和局部模型可以看出:对比结果均具有很好的一致性。
为了进一步检验转化前后模型的一致性,图3和4分别给出了采用SAP与ABAQUS两种程序计算得到的模态结果,从模态的变形与计算结果可以看出:第2、14、61和451阶振形不仅形似,而且自振频率计算结果比较相近,结果依次相差3.39%、4.42%、1.63%和2.09%。通过如上模态对比,表明分析结果同样具有一致性,由此进一步验证了SAP模型通过SAP2ABAQUS转化为ABAQUS模型后的精确性。
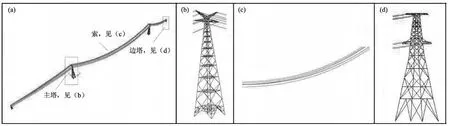
图1 采用SAP建立的有限元模型(a)整个结构体系;(b)主塔;(c)索;(d)边塔Fig.1 Finite element model established by using software SAP2000(a)the whole structure system;(b)main tower;(c)cable;(d)side tower
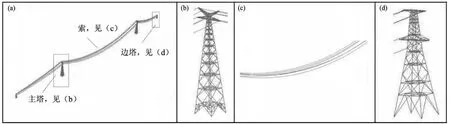
图2 采用SAP2ABAQUS生成的ABAQUS有限元模型(a)整个结构体系;(b)主塔;(c)索;(d)边塔Fig.2 ABAQUS finite element model generateded by using program SAP2ABAQUS(a)the whole structure system;(b)main tower;(c)cable;(d)side tower
综上所述,以上对比结果从该实际工程角度进一步验证了《结构动力弹塑性与倒塌分析(Ⅱ)》中开发的SAP2ABAQUS接口程序的现实性、有效性和可信性。
1.3 有限元模型对象的分析与确定
数值分析结果与有限元模型选取直接相关,不考虑3 000 m级长导线的模型可能无法确保计算结果的可靠性。本节针对这一实际工程,对不同边界条件的主塔(单塔、1塔2跨线、2塔1跨线和4塔3跨线)进行模态分析,以考察不同边界的主塔频率大小和振型形状(包括方向)的区别。

图3 SAP有限元模态分析结果(a)2阶模态;(b)14阶模态;(c)61阶模态(d)451阶模态Fig.3 Finite element modal analysis results by using software SAP(a)second order modal;(b)forteen order modal;(c)sixty-first order modal;(d)451st order modal

图4 ABAQUS有限元模态分析结果(a)2阶模态;(b)14阶模态;(c)61阶模态(d)451阶模态Fig.4 Finite element modal analysis results by using software ABAQUS(a)second order modal;(b)forteen order modal;(c)sixty-first order modal;(d)451st order modal
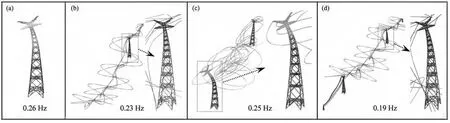
图5 不同有限元模型建立与模态(a)单塔;(b)1塔2跨线;(c)2塔1跨线;(d)4塔3跨线Fig.5 Establishment of different finite element model and their modal(a)single tower;(b)the tower with two over lines;(c)two towers with one over Line;(d)four towers with three over lines

表1 不同模型模态计算结果对比Tab.1 Comparision of modal analysis results for different finite element model
计算结果如图5和表1所示。综合分析,可以得到:
(1)与4塔3线计算结果相比,其他模型的频率最小相差14.6%,最大相差30.3%。这说明如此大跨度导线的质量等因素对主塔的影响不容忽视。
(2)悬链线索作为输电塔之间唯一连接,不均匀地震地面运动输入会导致不同主塔和边塔运动不一致,会对相邻塔产生影响。这属于客观事实。
(3)目前输电线路地震动多点激励研究基本局限于材料的弹性范围,所关注大多为内力、位移和加速度反应。尚未充分涉及到多点输入对结构体系破坏环节和倒塌模式的影响,尤其对大震和特大震作用下的情形关注较少。对于这部分内容研究,需要从结构体系出发,否则难以将各种因素考虑全面,甚至会导致对倒塌机制的认识有误。
综合上述分析,下文将以具有几何大变形非线性和刚度硬化时变性的整个结构体系为地震分析对象,并对其进行分析。
2 加载方式、理论根据和验证
2.1 加载方式与理论根据
隐式计算方法需要迭代而涉及收敛问题,对于几何大变形、弹塑性甚至倒塌等动力分析而言难于收敛甚至不收敛。显式计算方法不存在收敛问题,但是足够的计算精度需要积分步长满足如式(1)所示条件,而足够小的步长需要计算机具有足够强的计算能力。考虑到数值计算不收敛没有意义,因此这里选择足够强的计算机并通过足够小积分步长的显式方法进行计算。
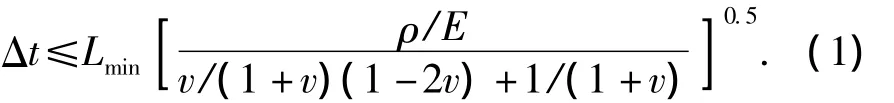
式中,Lmin、ρ、E和v分别表示结构体系中最小构件的尺寸、密度、弹性模量和泊松比。
不同于一般的结构体系,本文研究的体系中有超长的悬链线索,索的刚度与其当前的形状和受力关系较大。即具有刚度时变性,而且需要事先找形和施加重力使其具有初始刚度。在ABAQUS中,当前没有Explicit/Static计算方法,若直接采用隐式的General/Static方法重力初始找形,则无法续接给Explicit/Dynamic方法地震分析,这不同于上述的模态分析。为了克服这一问题,可以变换思路:本文采用Explicit/Dynamic间接实现重力作用下的静力效果,在理论上可采用动力分析法实现静力效果有两种思路:
(1)增加结构阻尼至足够大。采用该方法,对当前步的重力加载无影响,但会影响结构的阻尼参数而导致后续动力分析模型和计算结果失真。
(2)加载时间周期足够长。采用该方法,重力加载时间需要足够长,理论根据是长周期低频动力荷载对相对的短周期高频结构的作用效应等同于静力效果。另外一个理解角度:是促使加载幅值对反应限于静力贡献而避开荷载频率与结构发生共振产生的动力效果。
2.2 加载步长和方式验证
本节从计算精度角度,依据上述思路对积分步长和加载周期的有效性给出验证。
根据式(1)得到步长应满足 Δt≤1.71×10-5,这里取为 Δt=1.0 ×10-5,重力加载时间定义为T=10 s。所采用的方法是将Explicit/dynamic与Genneral/static分析结果的应力图和变形图作比较。结果如图6所示,通过对比可以看出:无论是应力或是变形,均具有很好的一致性。由此说明计算结果精度足够,从而验证了通过Explicit/dynamic法实现Genneral/static分析效果的可靠性。
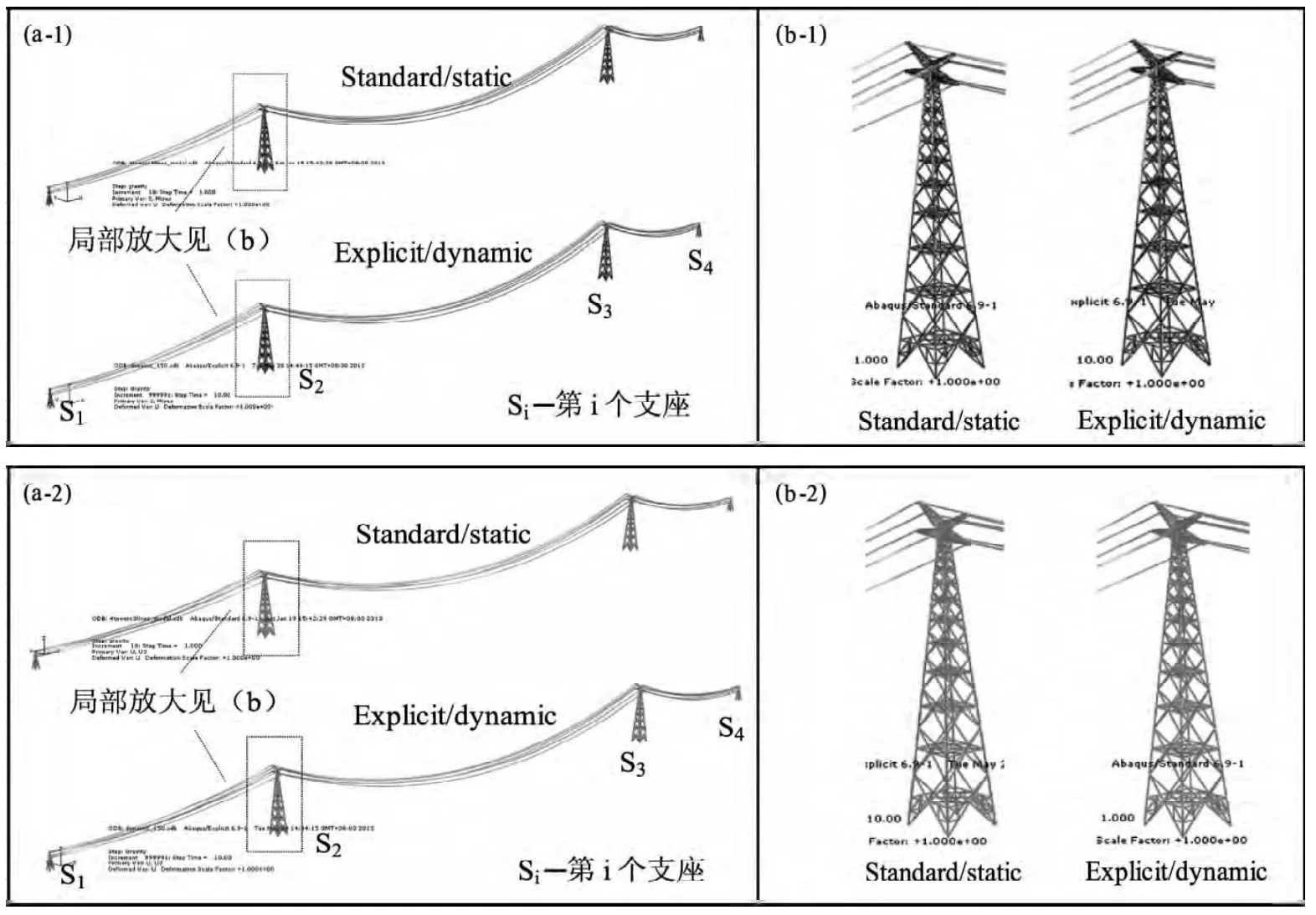
图6 Mises应力对比图(a)及竖向变形云图对比(b)(a-1)、(a-2)整体模型;(b-1)、(b-2)局部放大图Fig.6 Comparison of Mises stress(a)and vertical deformation nephogram(b)(a-1),(a-2)whole model;(b-1),(b-2)partial enlarged detail
3 地表多点地震动
3.1 多点地震动理论模型与相干函数选取
基于地表谱的多点地震动理论模拟多点地震动,建立如式(2)所示功率谱矩阵和拟合反应谱时,涉及如下3个模型:
(1)地表规范反应谱,可直接依照电力设施抗震设计规范(GB50260-1996)。
(2)地表目标功率谱,如式(3)所示(田利,李宏男,2010)。
(3)地表相干函数,为式(4)中γij(ω,d)。

式中,对角线元素是自谱,为实数,其物理意义是同样位置信号完全相关;非对角线是互谱,为虚数,其物理意义是不同位置信号之间幅值与相位不完全相关。
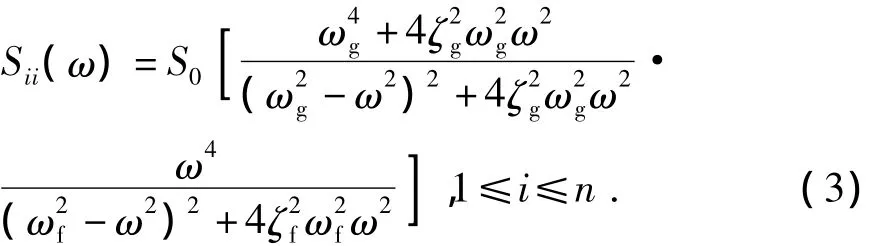
式中,S0为谱强度因子;ωg和ξg为场地的卓越频率和阻尼比;ω为圆频率;ωf和ξf为模拟地震动低频分量能量变化的参数。如上参数与场地类别、常/罕遇与设防等级有关。
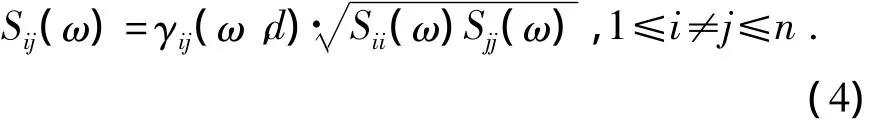
式中,γij(ω,d)是相干函数,是关于频率和不同位置之间距离的函数,其物理意义是不同频分不同两点之间的相干性。在自谱(目标功率谱)确定的条件下,互谱的计算则取决于相干函数。这时,相干函数合理与否将直接影响多点地震动的模拟结果,因此重要且关键。Hao模型具有较大影响力(Hao et al,1989),李英民等(2013)指出:Hao模型在低频段衰减较快,与真实记录地震动相干性有所差异。本文中一维多点地震动的模拟,采用的是如式(5)所示的Haricharidran-Vanmarcke模型(Harichandran,Vanmarcke,1986),主要是考虑到两点:(1)该模型能够体现出多点地震动在低频段的相干性比较平缓(李英民等,2013),衰减较慢(即在低频段有较小“平台段”),符合多点地震动实测记录之间客观相关特性。(2)低频段特性,对于大跨长周期(低频)结构影响更为重要。
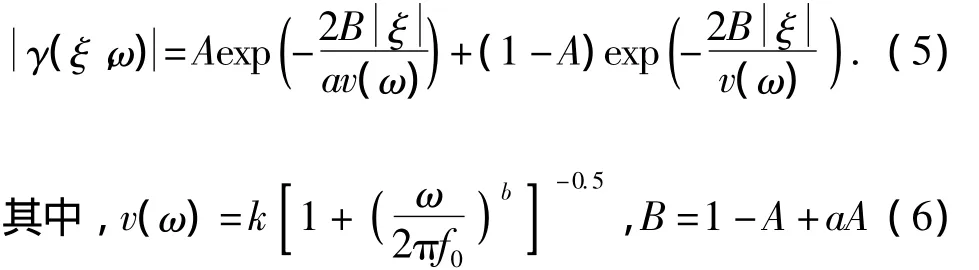
式中,A、a和 k均为模型参数,这里取为 A=0.736、a=0.147和k=5 210,v(ω)体现了相干性与频率关系(Harichandran,Vanmarcke,1986)。
3.2 地表多点地震动模拟与验证
考虑到2.1节内容,本文对所开发的MEMS_b①柳国环,陆新征,国巍,等.考虑地震动多点激励与材料应变率效应的主跨300米级独塔斜拉桥弹塑性分析.计算力学学报待刊.的V2012.8版本程序更新至 V2013.5新版本(柳国环等,2014b),如图7所示。
塔—线体系支座处的多点地震动位移时程曲线模拟结果如图8所示。为了验证地震动模拟结果的有效性并考虑篇幅有限,图9中给出了两个主塔支座的加速度时程、功率谱拟合、相干函数验证以及规范反应谱的拟合曲线,说明模拟结果比较理想。

图7 基于地表功率谱的多点地震动模拟程序(MEMS V2013.5)Fig.7 Visual Program MEMS V2013.5 for generating multiple earthquake motions simulation based ground power spectrum
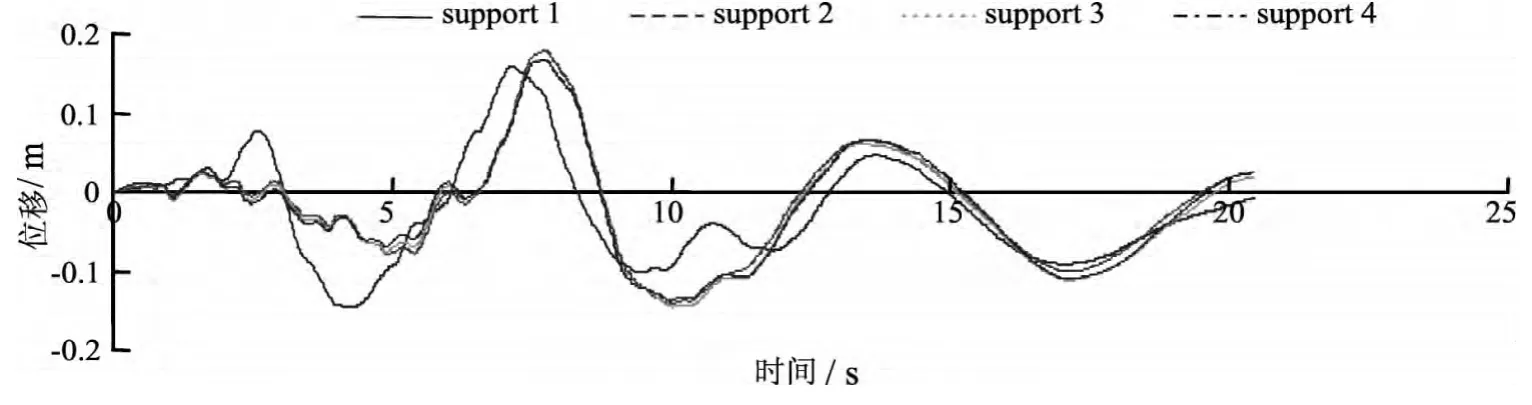
图8 支座处多点地震动位移时程Fig.8 Multi-points earthquake motion displacement history at each support
4 超大震作用下结构体系的倒塌模式
当前执行的《电力设施抗震规范》(GB50260-1996)仅给出了设计基本加速度,烈度9度时加速度峰值(PGA)为0.4 g。同样,目前所执行的《建筑抗震设计规范》(GB50011-2010)给出了常遇和罕遇的加速度时程最大值,9度罕遇时PGA为0.62 g。然而,近期发生的几次地震(如汶川8.0级地震、日本7.1级地震)的地震动加速度峰值均大于以上的规范值,甚至是倍数级,同时考虑到文中研究的塔—线体系属于超大跨超高的重要复杂生命线工程,因此进行了超大震作用下的结构反应分析,从而了解结构体系在极端荷载作用下的薄弱环节和倒塌的可能性。分析工况考虑一致输入和多点输入,考虑PGA为1.5 g,3.0 g和6.0 g 3种情形。计算结果如图10所示。

图9 模拟的多点地震动验证(a)支座2地震加速度;(b)支座3地震加速度;(c)支座2地震加速度功率谱验证;(d)支座3地震加速度功率谱验证;(e)支座2地震加速度反应谱拟合;(f)支座2和3点加速度相关性验证Fig.9 Verification of the simulated multi-points earthquake motions(a)earthquake acceleration of support 2;(b)earthquake acceleration of support 3;(c)earthquake acceleration power spectrum verification of support 2;(d)earthquake acceleration power spectrum verification of support 3;(e)earthquake acceleration power spectrum fitting of support 2;(f)earthquake acceleration correlation verification of support 2 and 3
由图10可以看出:
(1)从薄弱环节角度分析:开始薄弱位置均出现在塔腿部分,而且一致或多点输入以及地震动加速度峰值并未对薄弱区域产生明显影响。该现象表明,在超大震来临时需要重视塔腿部分。
(2)从倒塌破坏模式角度分析:多点输入计算结果明显区别与一致输入情形,包括倒塌破坏的方向和程度。该现象可表明,倒塌模式对多点输入敏感。
(3)从最终破坏部位角度分析:塔头和塔腰均未出现明显的局部破坏现象而是作为整体随塔腿共同坍塌。该现象可以表明,塔头和塔腰不仅未显示出薄弱之处而且对地震动输入模式和峰值不敏感。
(4)从破坏区域集中现象和能量角度分析:随PGA增大,地震输入能量增强而破坏程度加强,但均集中在塔腿部分而并未将能量明显分散到其他部位使其破坏严重。从这种现象可以推断,地震激励下结构体系的强弱分区明显,这与结构设计应使地震能量尽量均匀分布于结构体系的原则不符合,进而建议考虑结构体系在超大震作用下的结构形式选则问题,旨在最大限度避免超大震来临时给如此重要生命线电力工程可能带来的灾害。

图10 结构体系中主塔的地震反应(a)PGA=1.5 g;(b)PGA=3.0 g;(c)PGA=6.0 gFig.10 Seismic response of main tower of the structural system(a)PGA=1.5 g;(b)PGA=3.0 g;(c)PGA=6.0 g
5 结语
本文作为系列研究的第III部分工作,为了服务于工程,首先从工程实际角度验证了第I开发子程序以及第II部分开发接口的实效性,并结合结构体系在超大震作用下可能面临的问题,做了如下几方面工作:
(1)从实际工程角度,验证了所开发接口程序SAP2ABAQUS的转化准确性与高效性。
(2)从实际工程角度,验证了所开发子程序的可行性与现实性。
(3)明确给出、阐述并验证了长周期的Explicit/dynamic法实现Standard/static加载的静力效果,该途径理论合理、现实易行,本质可完全避免Standard/static与后续Explicit/dynamic动力分析不续接的现实问题。
(4)薄弱环节均出现在塔腿部分,对输入模式与加速度峰值不敏感,建议给予足够重视;薄弱环节倒塌破坏的方向和程度对受多点输入影响很敏感,不容忽视;塔头和塔腰均未出现明显的局部破坏现象而是作为整体随塔腿共同坍塌;地震激励下结构体系的强弱分区明显,这与地震能量尽量均匀分布于结构体系的原则不符合,进而建议考虑结构体系在超大震作用下的结构形式选则问题。
李英民,吴遮赛,陈辉国.2013.地震动的空间变化特性分析与修正相干模型[J].振动与冲击,32(2):164-170.
柳国环,练继建,国巍.2014a.结构动力弹塑性和倒塌分析(II):SAP2ABAQUS接口技术、程序开发与验证[J].地震研究,37(1):132-140.
柳国环,练继建,国巍.2014b.结构动力弹塑性和倒塌分析(I):滞回关系改进、ABAQUS子程序开发与验证[J].地震研究,37(1):123-131.
田利,李宏男.2010.基于《电力设施抗震设计规范》的地震动随机模型参数研究[J].防灾减灾工程学报,30(1):18-22.
GB 50011-2010,建筑抗震设计规范[S].
GB50260-1996,电力设施抗震设计规范[S].
Hao H,Oliveria,C S,Penzien..1989.Multiple - station ground motion processing and simulation based on SMART -1 array data[J].'Nuclear Enginering and Design.,111(3),293 -310.
Harichandran R S,Vanmarcke EH.1986.Stochastic Variation of Earthquake Ground Motion in Space and Time[J].Journal of Engineering Mechanics,112:154 -174.

