实时地震监测台网中Voronoi图生成算法的改进*

赵 瑞，刘希强

(山东省地震局，山东济南250014)

0 引言

建设地震监测台网的主要科学目的之一就是一旦地震发生后，第一时间开展地震速报工作。当前基于实时地震监测台网建立地震预警系统和地震应急控制系统在国际上已形成潮流。日本、美国、墨西哥、土耳其、意大利、瑞典、罗马尼亚、中国台湾等地震多发国家和地区发展了多套预警系统，如日本铁路UrEDAS系统、墨西哥SAS和SASO系统、美国ElarmS和PreSEIS系统、土耳其PreSEIS和SOSEWIN系统等，并有一些成功预警且收到减灾实效的先例(Gasparini et al，2007;Wu et al，2007;Allen et al，2009;殷海涛等，2012)。在地震预警技术中，Voronoi图(以下简称V图)在地震事件触发判断、地震定位等方面已得到初步应用(Rydelek，Pujol，2004;Horiuchi et al，2005;Satriano et al，2008;王庆民等，2012);同时在地理信息系统、计算机图形学、气象学、虚拟实现、机械工程、机器人等领域也有着广泛的应用(刘金义，刘爽，2004;范会川等，2010)。

V图最早可追溯至1908年，Georgy Voronoi首先在数学上限定了每个离散点的有效作用范围，提出了二维 V图(Voronoi，1908)。1934年，Boris Delaunay提出Delaunay三角网，V图与Delaunay三角网格互为对偶图，可通过Delaunay三角网格寻找与每个离散点相关的三角形，顺序连接每个三角形的外接圆心得到多边形，即为V图(孙继忠等，2010)。经过众多专家学者的研究，Delaunay三角网的生成算法日趋成熟。目前主要有分割—归并法、逐点插入法和三角网格生长法及每种方法的改进算法，其中前两种方法应用较多(Aurenhammer，1991;Delaunay，1934;Okabe et al，1994)。每种算法各有其优缺点，分割—归并算法适合离散点较多的情况，但该算法含有大量迭代运算，空间复杂度高，并且凸壳形成时，算法较复杂，时间复杂度也较高(周培德，2000)。逐点插入法算法简单，占用内存少，空间和时间复杂度不高，但没有很好地解决凸壳问题。三角网格生长法算法简单，以基边为循环条件，产生凸壳时较困难，同时易产生边与边相交，不利于Delaunay三角网格优化。武晓波等(1999，2000)将逐点插入法与分割—归并法相结合，提高了计算速度，降低了算法复杂度，但同样没有很好解决凸壳、初始三角网的生成问题。王强等(2010)在此合成算法的基础上，提出一种改进的Delaunay三角网生成算法，采用虚拟四边形凸壳，较好解决了初始三角网的生成问题，但是在删除虚拟顶点时，若想保证实际凸壳的正确性，必须提前在程序中对离散的数据点进行预处理排序，排序原理没有给出很好的说明，同时采用这种合并算法对Delaunay三角网优化时，复杂度高于其它算法。

在实时地震监测台网中，当在台站中断记录时段发生地震，利用V图进行地震定位必须要调整V图布局，若考虑所有正常台站重新计算V图则复杂度会明显加大，如何能在不改变全局V图的前提下，快速完成对中断台站V图单元的重新剖分，又不失精度，是地震预警系统中需要解决的问题。

1 V图生成算法

以山东测震台网79个台站为例，生成V图的主要技术思路是选择算法较简单的逐点插入法，采用向量关系解决节点定位(王强等，2010)，同时对点集进行预处理、Delaunay三角网生成进行改进，从而保证凸壳的客观性。

1.1 初始凸壳的生成

采用虚拟矩形方式生成初始凸壳，由4个顶点(［Min(x)、Min(y)］、 ［Min(x)、Max(y)］、［Max(x)、Min(y)］、［Max(x)、Max(y)］)形成矩形，同时判定顶点是否属于原有节点，如果不属于，则将该虚拟顶点加入到离散点集进行循环计算。分两种情形生成初始三角形:一是当4个顶点不相重复，则按图1a生成初始三角形;二是当4个点有相重点时，则按图1b生成初始三角形。根据节点所在位置，在图1上显示R1、R2、R3和R4四个区域。

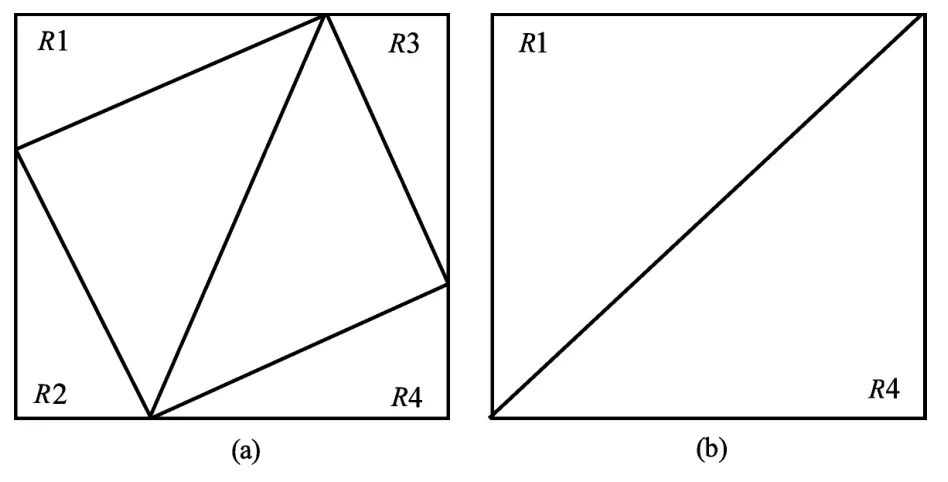
图1 初始三角形生成图情形1(a)和情形2(b)Fig.1 Generating the initialization triangle in situation 1(a)and situation 2(b)

1.2 点集预处理

为保证凸壳的有效生成，即删除原始虚拟凸壳顶点时不出现凹陷面，需要在逐点插入算法前，对节点进行排序。图2a中当前节点M位于第R1区域时，连接MA，MB，MC生成3个新的三角形区域①、②、③。图2b中当后节点N位于①区时，做线段CM的延长线至AB，交点为C1，当点N位于△C1BM内部时(图2b中阴影区)，能够满足BNMC的连线为凸面，则将N点排在M点后，反之，调换M与N点顺序。图2c中当点N位于②区时，做线段BM的延长线至AC，交点为B1，当点N位于△C1BM内部时，点BMNC的连线为凸面，则将点N排在M点后，反之，调换M与N点的顺序。当点N位于图2d阴影区内时，点BMC的连线均为凸面，则点N排在点M后。总之，当点N位于图1第R1区中如图2e所示阴影区内时，不用调换M与N点的顺序，反之需要调换顺序。同理，当点N位于图1第R2、R3和R4区域内的阴影区时，不需要调换M与N点的顺序(图2f～h)。

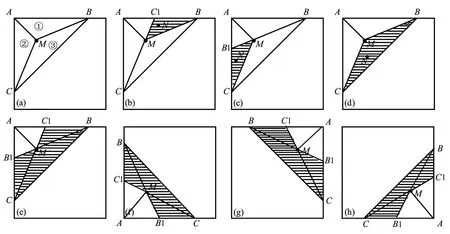
图2 点集预处理(a)M点位于R1区;(b)N点位于R1区中①区;(c)N点位于R1区中②区;(d)N点位于R1区中③区;(e)M点位于R1区;(f)M点位于R2区;(g)M点位于R3区;(h)M点位于R4区Fig.2 Preprocessing of point set(a)point M locates in zone R1;(b)point N locates in zone①of zone R1;(c)point N locates in zone②of zone R1;(d)point N locates in zone③of zone R1;(e)point M locates in zone R1;(f)point M locates in zone R2;(g)point M locates in zone R3;(h)point M locates in zone R4

1.3 逐点插入算法

根据王强等(2010)向量叉乘算法来判定点与三角形的位置。逐点插入时，每当新边、新三角形生成时，其编号权重设置为1。

1.4 Delaunay三角剖分优化算法

图3 Delaunay三角优化前(a)和优化后(b)Fig.3 Delaunay triangles before(a)and(b)after optimization

判断新生成的三角形是否为Delaunay三角形，即判断是否满足Delaunay三角形的空圆特性。首先判断四边形ABCD是否为凸四边形。为避免复杂的平方、开方计算，同样引入向量叉乘的概念。如图3所示有两个待优化的三角形ABD和BCD，连接AD，DC，CB，AB，得到 4个向量，如式(1)所示:

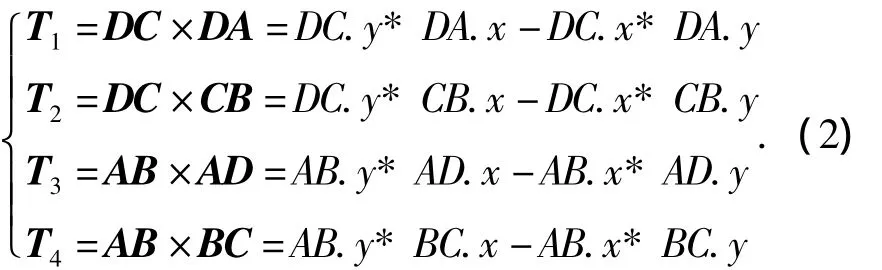
当四边形为凸四边形时，向量DA、CB在DC的同侧，并且向量AD、BC在AB的同侧，即T1与T2同号，且T3与T4同号(如式(2)所示)。确定为凸多边形后，分别求取△ABD、△BDC的外接圆圆心，判定是否满足空圆性。如果圆内有其他顶点，则交换四边形的对角线。原△ABD及△BDC的权重设置为0，边BD的权重设置为0，新生成的两个三角形，即△ADC及△ABC的权重设置为1，边AC的权重设置为1。

为降低Delaunay三角网格优化的复杂度，在逐点插入过程中进行优化。当所有离散点插入之后，再次对全体三角形进行优化，以期全部达到Delaunay三角剖分的准则。按照本文选取的研究区域(33.0～40.0°N，114.5～122.5°E)，将经纬度转换成直角坐标，研究范围为800 km×800 km。由山东地区测震台网生成的Delaunay三角剖分图见图4。

图4 由山东测震台网生成的Delaunay三角剖分图Fig.4 Delaunay triangulation diagram generated by Shandong Seismic Network

1.5 V图生成算法

存储每个台站所涉及三角形的个数及编号，按一定顺序对三角形外接圆心进行排序连接，即得到此台站的V图单元。同理，依次遍历所有台站，得到研究区域的V图见图5。

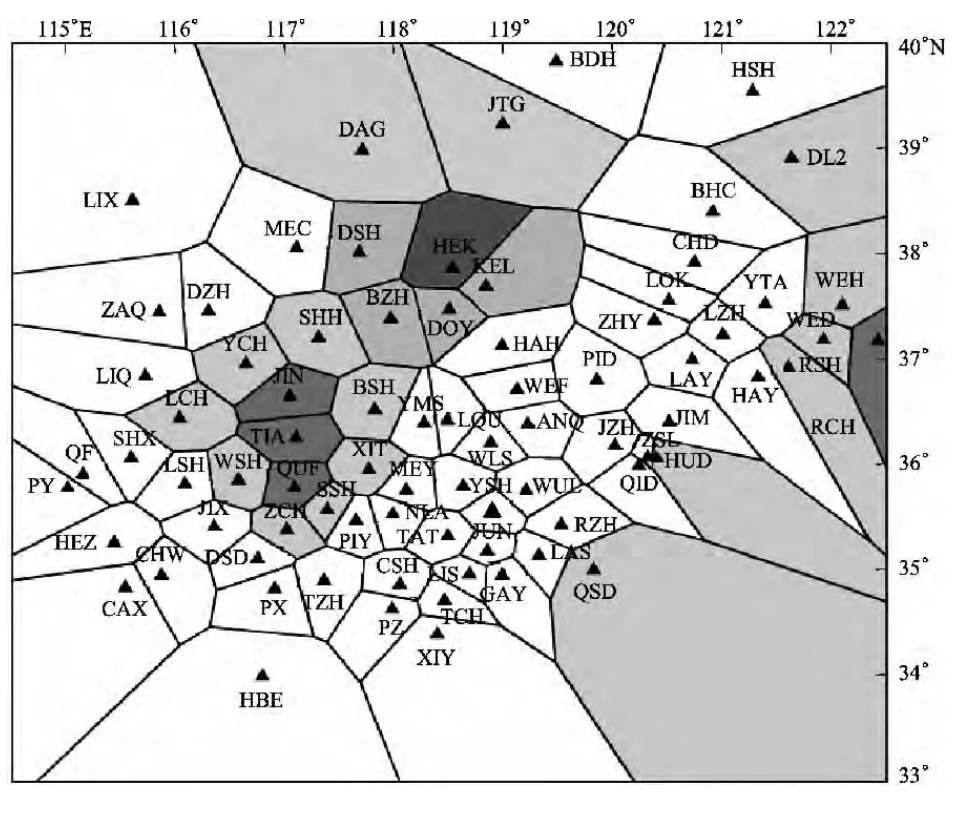
图5 由山东测震台网生成的Voronoi图Fig.5 Voronoi diagram generated by Shandong Seismic Network

2 台站中断时V图生成算法

在实际地震监测台网运行中，地震台站通常会因为中断或其他原因未记录到波形信号，如果地震恰发生在中断台站所在的V图单元内，则根据首先触发台站判定地震发生的区域时会产生较大的震中判定误差，从而影响地震定位的精度。所以在地震发生时需要实时判定正常运行台站的数量，快速准确地对中断台站的V图单元进行调整和归并。

本文给出3种台站中断例子，以说明V图生成算法及其结果有效性。假设有5个台站中断，分别是55号曲阜台(代码QUF，下同)、64号泰安台(TIA)、35号济南台(JIN)、56号荣成台(RCH)、31号河口台(HEK)，5个中断台站中HEK台属于孤立点，且属于网内的台站中断情形;JIN、TIA和QUF台属于片区中断台;RCH台属位于凸壳边界上台站中断情形(图4)。

首先判断中断台站是否为孤立中断点，从而保证因台站中断所形成的中断区域边界顶点均为运行良好的台站。将此区域内的三角形及边的权重设置为0，形成一个空区(图6a)，记录此空区边界上的点号及边号。当中断台站处于网内时，空区为封闭区域(图6b、c)，当中断台站处于网缘时，只有边界线，为半封闭区域(图6d、e)。当多个中断台站相邻时，此空区不一定为凸多边形，有可能存在凹陷的边界(图6c)，这时无论采取分割—归并法、逐点插入法或传统的三角网格生长法均不能完全保证空区边界点所重新形成的凸壳与空区边界线重合，并且易存在空区新凸壳与空区边界线相交的情况，这为小空区内Delaunay三角剖分、V图生成增加了难度。笔者在传统的三角网格生长法上提出了一种改进方法，使其保证空区凸壳的完整，步骤如下:

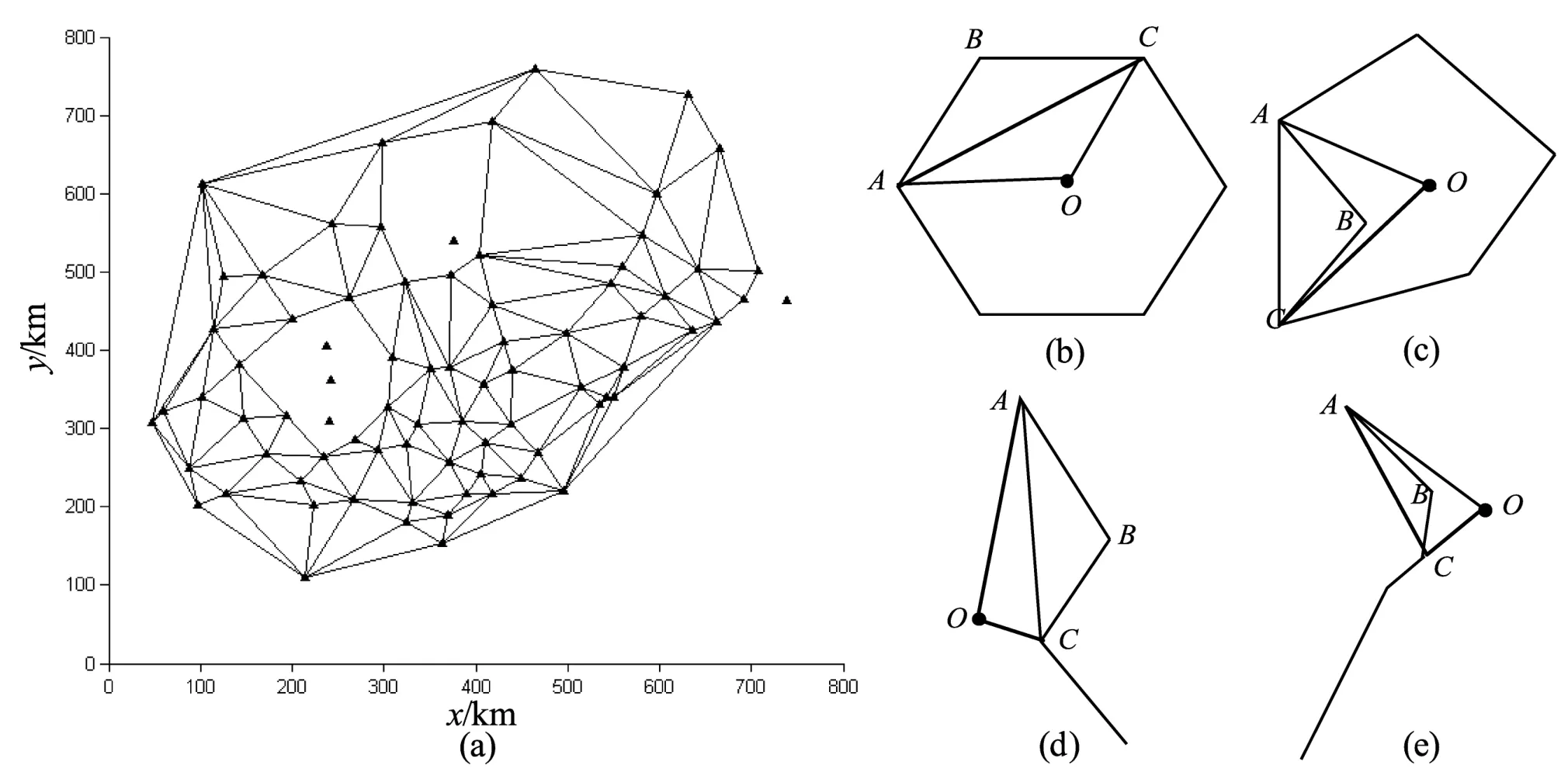
图6 中断台站形成的空区图以及四种不同情况下三角形形成示意图(a)空区图;(b)中断台站处于网内时，形成封闭区域情形1;(c)中断台站处于网内时，形成封闭区域情形2;(d)中断台站处于网缘时，形成半封闭区域情形1;(e)中断台站处于网缘时，形成半封闭区域情形2Fig.6 Empty areas diagram formed by the interrupt stations and the schematic of triangular generated in four different cases(a)empty area;(b)forming a enclosed area under the case 1 when the interrupt stations in the network;(c)forming a enclosed area under the case 2 when the interrupt stations in the network;(d)forming a semi-closed area under the case 1 when the interrupt stations in the network edge;(e)forming a semi-closed area under the case 2 when the interrupt stations in the network edge

(1)如图6b～e所示，中断点设为点O，选取空区中任意两条相交边AB、BC，当AO、AC在AB边同侧且CA、CO在CB边同侧，即T5与T6同号，T7与 T8同号时，连接 AC形成新三角形△AOC、△ABC(见图6b、6d)，反之不能形成新的三角形，如图6c、6e所示。

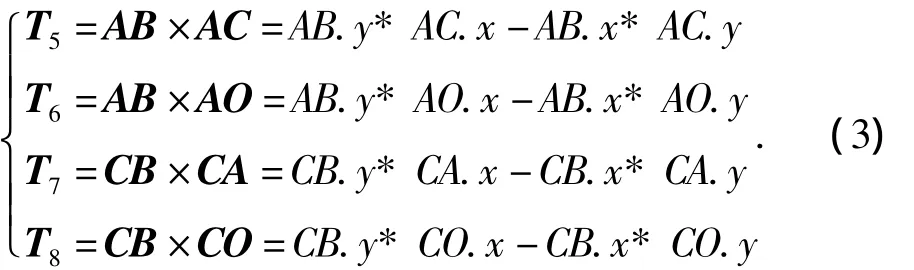
(2)当空区内所有三角形形成后，在空区内对其进行优化，使之成为Delaunay三角形。针对图6a中存在5个中断台站的情形，应用上述思路，生成的新的Delaunay三角剖分图见图7a，3个空区新生成的三角形用不同颜色标识出。

(3)遍历所有台站，生成新V图(图7b)，其中由于台站中断而涉及V图变化的区域用不同颜色给出。

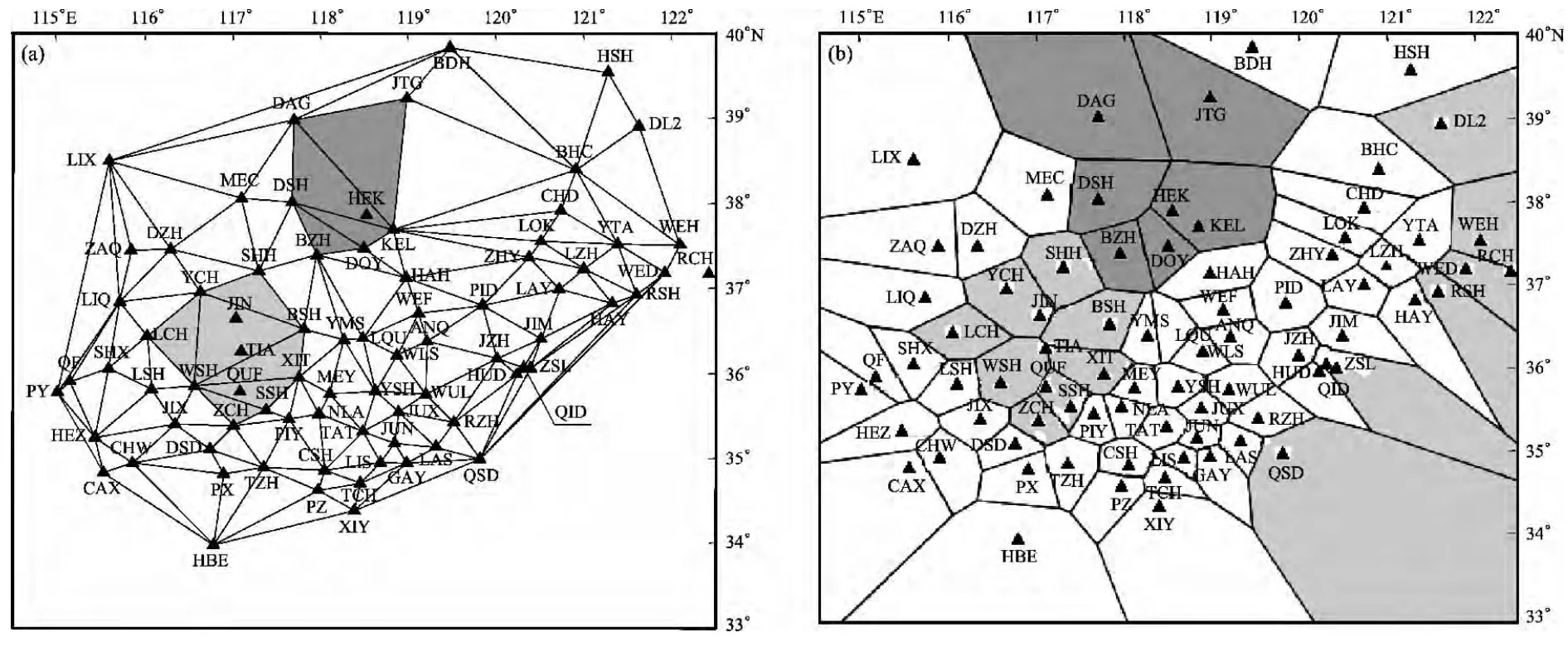
图7 考虑地震台站中断时生成的Delaunay三角剖分图(a)和新生成的Voronoi图(b)Fig.7 Delaunay triangulation(a)and the new Voronoi diagram(b)generated by considering the interrupted seismic stations

3 计算时间测试

为测试算法改进后的实际效果，我们进行了计算时间的测试，这也是在地震预警系统中必须解决好的一个科学问题。本文程序编写采用Fortran语言，时间对比均采取相同的硬件条件(联想台式机，主频2.83G)。下面分为两种情况进行讨论:

第一种是台站不存在中断的情况，采用改进后的逐点插入法与传统的逐点插入法进行对比。分别模拟1 000个、2 000个、5 000个、10 000个节点数据，运算得到Delaunay三角网格的CPU计算时间，对比如表1。

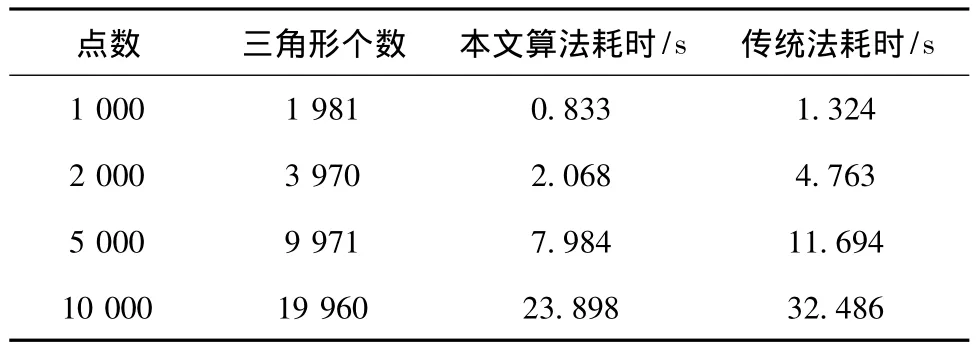
表1 Delaunay三角网格剖分算法改进前后对比表Tab.1 The comparison of delaunay triangulation algorithm before and after improvement

第二种是模拟山东地区存在5个中断台站，除去中断点，其余74个台站点重新剖分生成Delaunay三角网格与本文提出的局部采用改进后的三角网格生长法所用的时间进行对比分析。前者生成的Delaunay三角网格如图8所示。这两种方法所用的时间分别是0.35和0.10 s，生成V图的计算时间分别是0.52 s和0.15 s。

图8 除去5个中断台站后新生成的Delaunay三角剖分图Fig.8 The new generation Delaunay triangulation by removing five interrupt stations

通过两种计算时间对比，可以看出本文提出的V图生成算法优于传统的逐点插入法，在实际台网中，台站数量较少的情况下，基本上是瞬间完成的，并且地震台站中断时，局部采用改进后的三角网格生长法与除去中断点、重新剖分Delaunay三角网格得到的结果是一致的，但在计算用时上优于后者。

4 结语

本文对实时地震监测台网V图的逐点插入算法的细节进行了梳理，明确了点集预处理的准则，改进了Delaunay三角网格优化算法，提高了计算速度，并且考虑了实际台网运行过程中，地震台站中断时，V图重新生成的情况。其突出的优点是在不改变全局V图的前提下，局部区域采用三角网格生长法，完成对中断台站V图单元的重新剖分，即使在网缘台站中断的情况下，也能有效地约束凸壳的生成。通过计算时间的对比，可以看出在同等效果的基础上，计算用时要优于除去中断台站，重新剖分Delaunay三角网格。

V图在地震监测预报中具有潜在应用前景，如根据触发台站所在V图单元的集中性判定是否有地震事件发生，根据V图单元面积，搜索得到区域内相关地理信息及应急资源信息，同时结合其它台站记录信息，迅速判定震中位置，为地震早期预警系统提供有效的技术支持。

本文在撰写过程中得到国家科技支撑课题组(2012BAK19B04)和地震科技星火计划项目组(XH12029)成员的帮助，在此表示衷心感谢。

范会川，周慧娟，贾利民.2010.Voronoi图和Delaunay三角网在铁路应急管理中的运用［J］.中国科技信息，(8):245－247.

刘金义，刘爽.2004.Voronoi图应用综述［J］.工程图学学报，25(2):125－132.

孙继忠，胡艳，马永强.2010.基于Delaunay三角剖分生成Voronoi图算法［J］.计算机应用，30(1):75－77.

王强，郑逢斌，乔保军，等.2010.一种改进的Delaunay三角网生成算法［J］.计算机应用与软件，27(8):138－140.

王庆民，刘希强，沈得秀.2012.Voronoi图和双曲线联合方法在地震快速定位中应用［J］.西北地震学报，34(3):234－244.

武晓波，王世新，肖春生.1999.Delaunay三角网的生成算法研究［J］.测绘学报，28(1):28 －35.

武晓波，王世新，肖春生.2000.一种生成Delaunay三角网的合成算法［J］.遥感学报，4(1):32－35.

殷海涛，刘希强，李杰，等.2012.现今地震预警技术及其在国内发展状况的探讨［J］.中国地震，28(1):1－9.

周培德.2000.计算几何算法分析与设计［M］.北京:清华大学出版社.

Allen R.M.，Gasparini P.，Kamigaichi O.，et al.2009.The Status of Earthquake Early Warning aroud the World:An Introductory Overview［J］.Seismol.Res.Lett.，80(5):682 －693.

Aurenhammer F..1991.Voronoi diagrams-a survey of a fundamental geometric data structure［J］.ACM Computing Surveys，23(3):345－405.

Delaunay B Sur la Sphere Vide.1934.Bulletin of the Academy of Sciences of the USSR［J］.Classe des Sciences Mathematiques et Naturelles，8:793 －800.

Gasparini P，Manfredi G，Zschau J.2007.Earthquake Early Warning System［M］.Germany:Springer-Verlag，249 －282.

Horiuchi S.，Negishi H.，Abe K.，et al.2005.An Automatic Processing System for Broadcasting Earthquake Alarms［J］.Bulletin of the Seismological Society of America，95(2):708 －718.

Okabe A.，Boots B.，Sugihara K..1994.Nearest neighborhood operations with generalized Voronoi diagrams:A review［J］.International Journal of Geographical Information Systems，8(1):43 －71.

Rydelek P.，Pujol J..2004.Real-Time Seismic Warning with a Two-Station Subarray［J］.Bulletin of the Seismological Society of America，94(4):1546－1550.

Satriano C.，Lomax A.，Zollo A..2008.Real-time evolutionary earthquake location for seismic early warning［J］.Bulletin of the Seismo-logical Society of America，98(3):1482 －1494.

Voronoi G..1908.Nouvelles Applications des Parameters Continus，a la Theorie des Formes Quadratiques.Deuxieme Memorte:Recherches sur les Parrallelloedres Primitifs［J］.Jounal fur die Reine und Angewandte Matnematik，134:198 －287.

Wu Y.M.，Kanamori H.，Allen R.M.，et al.2007.Experiment using the tau-c and pd method for earthquake early warning in southern California［J］.Geophys.J.Int.，170:711 －717.