优化的准正弦平顶调制波PWM过调制新技术
王榕生
(福州大学电气工程与自动化学院,福建福州350116)
0 引言
SVPWM(space vector pulse width modulation,SVPWM)具有直流母线电压利用率高的优点而得到广泛应用,其过调制算法也因此受到更多关注与研究[1-12]。现有基本方法是将过调制区分为两种模式[1-8]。调制度 M∈[0.906,0.952]区间为模式Ⅰ,其实际输出空间矢量轨迹位于基本矢量构成的正六边形边界与内接圆之间,在每个扇区的轨迹又分为两部分,一部分为正六边形边界,另一部分为连接该边界两端的圆弧即补偿区。PWM(pulse width modulation,PWM)算法主要有补偿区外的空间矢量按比例收缩及查表确定与调制度M对应的补偿角等步骤;M∈[0.952,1]区间为模式Ⅱ,PWM算法主要有查表确定与调制度M对应的保持角即空间矢量在正六边形顶点的停留时间以及非停留区的矢量收缩等。所述算法还涉及除法运算,并且包括确定空间矢量所在扇区号等必要步骤。由此看出,SVPWM过调制算法的构成颇为复杂。
PWM算法应力求简单,这是评估其优劣的一个重要指标。为此,本文另辟思路,尝试构建一种称之为“准正弦平顶新调制波”。采用三角载波采样生成三相PWM,可使线性区内的最大输出线电压基波幅值较SPWM(sinusoidal pulse width modulation,SPWM)高19%,显著提升了直流电压利用率。在过调制区,则采用扩大调制波平顶宽度的方法继续增大所含基波,直至方波输出。为保持基波与调制度M间的线性关系,将平顶宽与M的数值关系预先制表,通过查表获取相应值。新方法具有算法简单、THD(total harmonic distortion,THD)低的优点。数值分析与实验结果证实了其有效性。
1 准正弦平顶调制波
为提高调制波所含基波分量,构建一种新型调制波如图1所示。
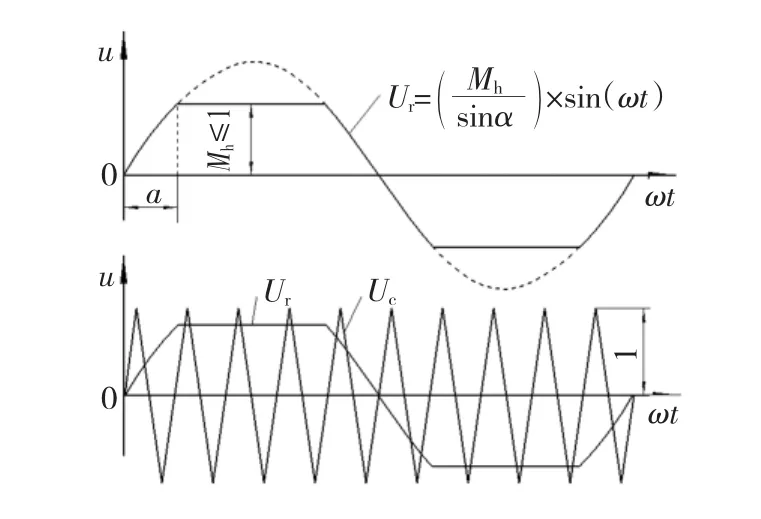
图1 准正弦平顶调制波Fig.1 Flat top quasi-sinusoidal modulating waveform
调制波Ur为正弦波削去顶部后所得波形,中间部分为平顶波,两腰为正弦波。Uc为三角载波,其幅值为1。调制波Ur的数学描述为


赋于调制波平顶特征必伴生谐波负面影响,其程度由谐波失真度衡量,即
电压谐波失真度
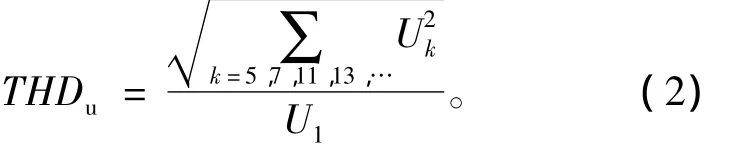
电流谐波失真度

式(2)、(3)中:U1为线电压基波幅值;k为谐波次数;Uk为k次谐波幅值。因调制波具有1/4周波对称且线电压不含有3次及其倍数次谐波,所以k为非3倍次的奇数。
由于图1调制波所含谐波经由PWM传出,对负载产生不良影响,其中影响最大的属低次谐波,因此应考查各低次谐波随α的变化情况。根据傅里叶公式,计算得出基波及5、7、11、13次谐波分量的相对值(幅值/Mh)、谐波失真度THDu与THDi(累计谐波至53次。)随α的变化曲线,分别如图2、图3、图4所示。
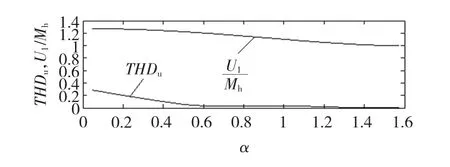
图2 THDu与基波随α变化曲线Fig.2 Variation of THDuand fundamental component with α

图3 THDi随α变化曲线Fig.3 Variation of THDiwith α

图4 5、7、11、13 次谐波随 α 变化曲线Fig.4 Variation of 5th、7th、11th、13th harmonic component with α
图示结果表明,增大平顶宽度即减小α有利于提升基波分量,但伴生的谐波影响应予以抑制。谐波影响随α呈现起伏变化的特征表明客观存在着寻优空间,即可以在提升基波分量的过程中使谐波影响相对最小。可以看出,当α=0.658时,THDi有一个极小值,并且THDu也在该点附近取得极小值,对应的基波相对值达1.19。有影响的低次谐波相对值如表1所示,其中影响最大的5次谐波为0,7次谐波仅为0.033 7。综合所有情况,有理由认为在α=0.658取值下的调制波为最佳。
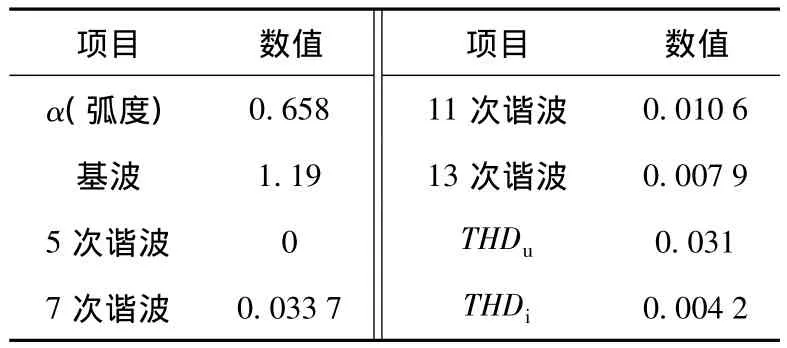
表1 各谐波分量及谐波失真度值Table 1 Harmonic component and THD
2 PWM算法
确定了最佳调制波之后,对三角载波进行调制,采用不对称规则采样法计算PWM。对调制度定义为

式中:U1为线电压基波幅值;Ud为直流母线电压。根据调制度M变化范围,将PWM分为两个调制区。
2.1 线性区(0≤M≤1.19)
保持α=0.658不变,当调制波高度Mh由0→1变化时,对应M的变化为0→1.19,在此范围内的PWM的基波值随Mh线性变化,脉冲计算公式为

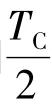
2.2 过调制区 (1 . 19<M≤)


图5 α角及1/sinα随M变化曲线Fig.5 Variation of α angle and 1/sinα with M
3 谐波数值分析
为得出谐波影响,应先按式(5)、式(6)计算出PWM线电压波形,再应用傅里叶公式计算其中的各次谐波。取载波比N=33,在M∈[0,1.19]线性区按所述步骤进行计算,得出准正弦平顶调制波PWM的线电压基波及有影响的N±2、N±4、2N±1等次谐波的相对值(幅值/Ud)随M的变化关系,如图6所示。
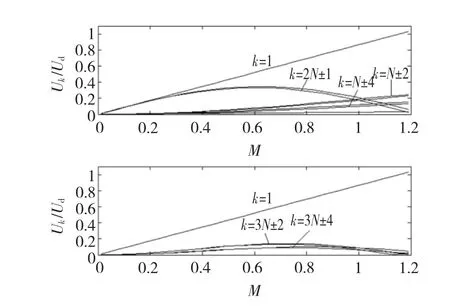
图6 N ±4,N ±2,2N ±1、3N ±4、3N ±2 次电压谐波分量与M的关系(N=33)Fig.6 Variation of the N ±4,N ±2,2N ±1、3N ±4、3N ±2 voltage harmonic component with modulation index M(N=33)
与具有相同载波比N=33的SPWM谐波(图略)相比较,两种PWM的2N±1次谐波基本相同,且N±2次谐波有相同变化趋势。然而,因调制波的非正弦性,使图6的PWM谐波不仅包含载波引起的各次谐波还包含调制波本身含有的谐波,因此谐波相对丰富,相较于SPWM而言有影响的谐波尚有N±4次。但从数值上比较,SPWM的N±2次谐波值明显大于图6同次谐波,当M=1时,其幅值大43%以上。总观两种PWM的谐波群,可以看出准正弦平顶调制波PWM的谐波呈现“多而小”的特征,而SPWM则呈现“少而大”的特征。为考察两种PWM谐波总影响,通常办法是按式(2)、式(3)分别求出 THDu及 THDi[12-17]。
图7示出了两种PWM的THDu及THDi随调制度M的变化曲线(累计谐波至200次),其中SPWM的M∈[0,1]。结果表明,二者 THDu值很接近。THDi值对比大体以M=0.55为界,当调制度M>0.55时,准正弦平顶调制波PWM线电压THDi值小(优)于SPWM 的THDi;而当M <0.55时,其THDi值转为大于SPWM,但最大增加量不超过2.2%。因此,二者在M∈[0,1.19]线性区内的 THDi指标可视为总体相当。当M∈[1.19,4/π]过调制区时,调制波趋于方波,其5、7次等低次谐波增长较快而使THDi急速攀升。

图7 两种PWM的THDi及THDu对比(N=33)Fig.7 Comparison of THDiand THDucurves with two PWM(N=33)
4 实验验证
为验证新技术有效性,搭建了以TMS320LF2407A为控制核心的三相电压型逆变系统,按式(5)~式(6)算法编制了三相PWM的DSP计算软件,其载波频率为1.65 kHz,死区时间4.2 μs。直流母线电压311 V,负载电机功率为3 kW。
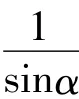
图8为实测的PWM线电压与线电流波形。图9示出了实测U1与调制度M间的良好线性关系。
表2给出了图8(b)线电压基波及各次谐波幅值的实测与计算值对比情况。其中基波及有影响的载频附近的N±2、N±4次主要谐波值具有良好吻合。然而因实际PWM存在“死区”、母线直流电压脉动及DSP定点处理数据所产生的固有误差等因素的作用导致波形一定程度的失真,表现为那些数值较小的谐波的实测与计算值对比有明显不同。

图8 负载线电压与线电流实测波形Fig.8 Measurement of the load line-voltage and line-current waveforms

图9 U1=f(M)Fig.9 Variation of U1with M

表2 线电压基波与谐波幅值(M=0.978,N=33)Table 2 Line-voltage fundamental and harmonic component amplitude(M=0.978,N=33)
5 结语
1)通过构建准正弦平顶调制波并进行优化(使α=0.658),显著提升了调制波所含基波幅值,且有效抑制了谐波分量。在M∈[0,1.19]线性区的最大输出线电压基波幅值比SPWM高19%,比SVPWM高3.1%。谐波数值分析表明,其 PWM的THDi值在整个线性区与SPWM相比互见高低,总体相当;
2)新技术的PWM过调制算法的实质在于对调制波的平顶高Mh与α角(代表平顶宽)两个特征参数的不同操作,即线性区保持α角不变,改变Mh;过调制区保持Mh=1不变,缩小α直至方波输出,其间采用查表法保持线性输出特性,并且不同调制区使用同一PWM脉宽计算公式,算法简单明了。虽然相较于SPWM而言,脉宽计算公式包含有判别调制波采样角所在区间范围,进而选择不同公式的环节,但仍不失为简单的PWM计算公式;
3)实测三相PWM线电压基波分量与调制度M间有严格的线性关系。实验结果证实了新技术的优越性。
[1] 张立伟,刘钧,温旭辉,等.基于基波电压幅值线性输出控制的SVPWM 过调制新算法[J].中国电机工程学报,2005,25(19):12-18.
ZHANG Liwei,LIU Jun,WEN Xuhui,et al.A novel algorithm of SVPWM inverter in the overmodulation region based on fundamental voltage amplitude linear output control[J].Proceedings of the CSEE,2005,25(19):12 -18.
[2] 方辉,冯晓云,葛新来,等.过调制区内两电平SVPWM与CBPWM算法的内在联系研究[J].中国电机工程学报,2012,32(18):23-29.
FANG Hui,FENG Xiaoyun,GE Xinglai,et al.Relationship studies between two-level SVPWM and CBPWM in the over-modulation region[J].Proceedings of the CSEE,2012,32(18):23 -29.
[3] 吴芳,万山明,黄声华.一种过调制算法及其在永磁同步电动机弱磁控制中的应用[J].电工技术学报,2010,25(1):58-63.
WU Fang,WAN Shanming,HUANG Shenghua.An over-modulation algorithm and its application in PMSM drive with flux-weakening control[J].Transactions of China Electrotechnical Society,2010,25(1):58 -63.
[4] 谈龙成,李耀华,王平,等.适用于电流型变流器的空间矢量过调制策略[J].中国电机工程学报,2008,28(15):39 -43.
TAN Longcheng,LI Yaohua,WANG Ping,et al.An over-modulation strategy for space vector PWM current source converters[J].Proceedings of the CSEE,2008,28(15):39 -43.
[5] Lee D C,Lee G M.A novel over-modulation technique for spacevector PWM inverters[J].IEEE Transactions on Power Electronics,1998,13(6):1144 -1151.
[6] Joachim Holtz,Lotzkat W,Khambadkone A M.On continuous control of PWM inverters in the over-modulation range including the six-step mode[J].IEEE Transactions on Power Electronics,1993,8(4):546-553.
[7] Novel B S.Digital continuous control of SVM inverters in the overmodulation range[J].IEEE Transactions on Industry Applications,1997,33(2):525 -530.
[8] Subrata K.Mondal,Bimal K.Bose,Valentin Oleschuk,et al.Space vector pulse width modulation of three-level inverter extending operation into overmodulation region[J].IEEE Transactions on Power Electronics,2003,18(2):604 -611.
[9] 陆海峰,瞿文龙,张磊,等.基于调制函数的SVPWM算法[J].电工技术学报,2008,23(2):37 -43.
LU Haifeng,QU Wenlong,ZHANG Lei,et al.SVPWM algorithm based on modulation functions[J].Transactions of China Electrotechnical Society,2008,23(2):37 -43.
[10] 樊扬,瞿文龙,陆海峰,等.基于叠加原理的SVPWM过调制算法[J].清华大学学报:自然科学版,2008,48(4):461 -464.
FAN Yang,QU Wenlong,LU Haifeng,et al.SVPWM over-modulation algorithm based on superposition principle[J].Journal of Tshinghua University:Science and Technology,2008,48(4):461-464.
[11] 马志文,郑琼林,林飞.具有全调制范围的空间矢量脉宽调制算法研究[J].北京交通大学学报,2007,31(2):89 -93.
MA Zhiwen,ZHENG Qionglin,LIN Fei.Study of space vector PWM algorithm with entire modulation range[J].Journal of Beijing Jiaotong University,2007,31(2):89 -93.
[12] 王旭东,张思艳,余腾伟.SVPWM过调制中控制角算法的分析与应用[J].电机与控制学报,2010,14(12):63 -67.
WANG Xudong,ZHANG Siyan,YU Tengwei.Control angle algorithm of SVPWM over modulation analysis and application[J].Electric Machines and Control,2010,14(12):63 -67.
[13] S.R.Bowes,D.Holliday.Comparison of pulse-width-modulation control strategies for three-phase inverter systems[J].IEE Proc.-Electr.Power Appl,2006,153(4):575 -584.
[14] SIDNEY R.BOWES,Derrick Holliday.Optimal regular-sampled PWM inverter control techniques[J].IEEE Transactions on Industrial Electronics,2007,54(3):1547 -1559.
[15] SHI K L,LI H.Optimized PWM strategy based on genetic algorithm[J].IEEE Trans.Ind.Electron,2005,52(5):1458-1461.
[16] Sidney Robert Bowes.Novel real- time harmonic minimized PWM control for drives and static power converters[J].IEEE Transactions on Power Electronics,1994,9(3):256 -262.
[17] 王榕生,吴汉光.消谐法SHEPWM的谐波影响数值分析[J].电工技术学报,2011,26(9):183-189.
WANG Rongsheng,WU Hanguang.Numerical analysis of harmonic influence for selected harmonic elimination PWM[J].Transactions of China Electrotechnical Society,2011,26(9):183-189.

