非磁性次级直线感应电机力特性及涡流损耗分析

李硕， 范瑜， 吕刚， 李华伟

(北京交通大学电气工程学院，北京100044)

0 引言

磁悬浮列车是一种新型地面无接触高速交通运输工具，具有无污染、噪音小、能耗低、安全性高等特点［1］。但其铺设成本高，维护复杂，与既有线路不兼容等局限性，不适合大规模推广。

本文所研究的非磁性次级直线感应电机属于电动式磁悬浮系统。在电机初级绕组中通入三相对称交变电流产生运动的行波磁场，该磁场与非磁性次级导体中感应出的涡流磁场相互作用产生悬浮力，同时又可以提供驱动力［2］。

目前研究电动式磁悬浮系统以永磁电动式为主，如美国威斯康辛州立大学的 T.A.Lipo教授［3-4］及日本九州大学的藤井信南教授［5-6］都对永磁电动式磁悬浮系统进行了深入研究，但目前尚处于实验室研究阶段。永磁电动式磁悬浮系统产生悬浮力需要附加的推进系统使永磁体与非磁性导体板相对运动，存在附加的推进系统将产生很大的机械振动及机械噪声大等缺点。

非磁性次级直线电动式磁悬浮系统通过运动磁场相互作用可同时提供推进力和悬浮力，相对于永磁电动式磁悬浮具有不需要附加的推进系统，可避免产生机械振动，整体总量轻等优点。与现有复合次级直线牵引电机相比，由于采用非磁性次级，电机法向力不再是吸引力而表现为悬浮力，在实际运行中，在一定范围内可减轻车体重量，提高运载能力。

为了深入了解非磁性次级直线电机的性能特性，本文从经典电磁场理论分析出发，建立了非磁性次级直线感应电机的简化二维电磁模型，并对其磁场进行了分析，得到该电机的推进力、悬浮力及次级涡流损耗解析表达式;得到了推进力、悬浮力及次级涡流损耗的特性曲线。研究了次级损耗与输入电流幅值、频率、转差率之间的关系，找出较合适的工作区间。通过样机实验来验证理论分析的正确性。

1 电机的电磁模型

非磁性次级直线感应电机示意如图1所示。电机由初级铁心、绕组及非磁性次级(铝板)构成。考虑到非磁性次级直线感应电机的结构特点，建立其二维电磁场模型可有效减少计算量。

假定电机初级铁心磁导率无穷大;气隙磁场强度在z轴方向均匀恒定;电机初级铁心在x轴方向与次级相对运动，y轴为悬浮方向。并用表面电流层代替初级磁势，仅考虑基波分量忽略谐波影响。边端效应及齿槽效应通过卡氏系数进行修正［7］，即

式中:g为装置气隙长度;ge为考虑了各种主要影响因素的等效气隙长度;Kc为消除初级开槽对气隙中磁场分布造成影响的卡氏系数;Kg为消除磁场分布y方向上分布不均的波形畸变系数;Kt为补偿装置横向边端效应的横向边端效应系数。

图1 非磁性次级直线感应悬浮电机示意Fig.1 The scheme of non-magnetic secondary linear induction maglev motor

基于以上假设，在笛卡尔坐标系内，将参考坐标固定在初级铁心上，建立非磁性次级直线感应电机的二维电磁分析模型，如图2所示。

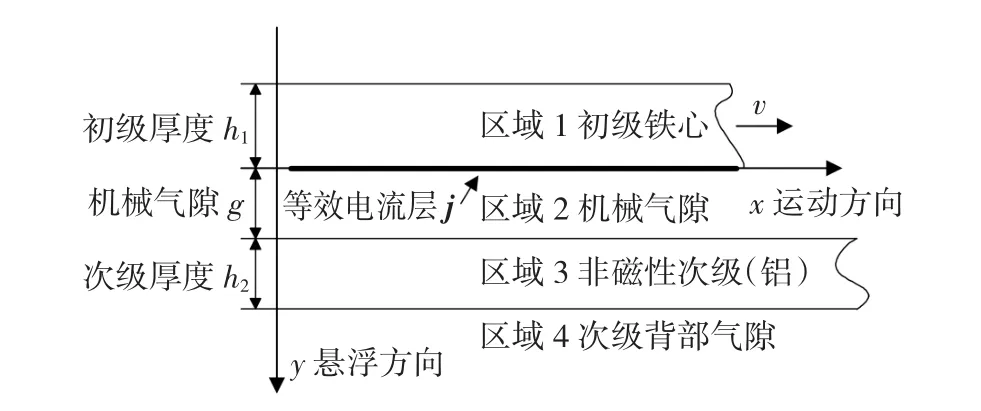
图2 电机二维电磁分析模型Fig.2 2D electromagnetic analysis model of the motor

将分布绕组等效为电流层，初级电流层j在区域1和区域2之间，在电机初级表面。其表现形式［8-11］为

式中:m为初级绕组的相数;W1为初级绕组每相串联匝数;kw1为初级绕组系数;p为初级绕组极对数;I为初级相电流有效值。

从稳态麦克斯韦基本电磁场理论出发［12～15］，则有

由欧姆定律得

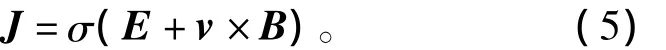
结合式(3)～式(5)可得二阶偏微分方程为

根据初级表面电流分布的周期性边界条件，磁场B具有x、y分量，次级涡流在z方向流动，B、J可具有如下形式，即

将式(7)代入式(6)得

其中，Q2=k2+ikμσv，μ、σ、v 分别为磁导率、电导率、行波线速度。式(8)和式(9)的通解为

由于不同区域的介质条件不同，需分别求解。区域 1 中，σ1=0，μ1= μFe，Q1=k，可得

区域2 中，σ2=0，μ2= μ0，μ0=4π ×10-7N/A2为真空磁导率，Q2=k，可得

区域 3 中，σ3= σAl=3.8 ×107S/m，μ3= μ0，可得

根据分界面边界条件，可确定以下方程，即

确定待定系数 a1、a2、b1、b2、b3为

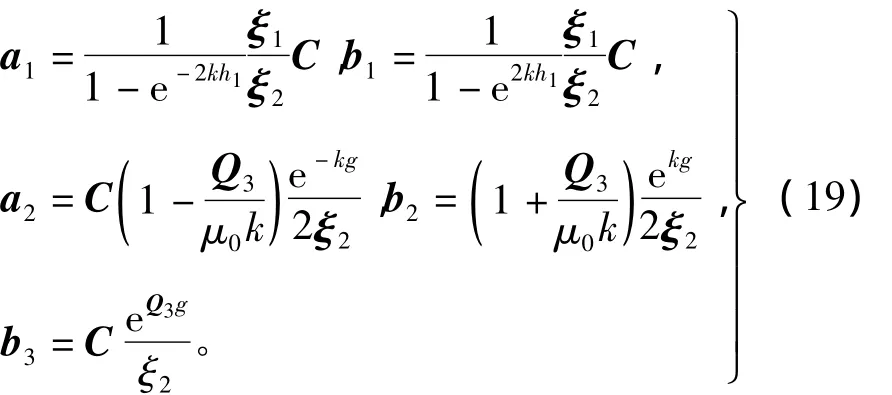
g为机械气隙高度;h1为初级铁心厚度。

2 力特性及损耗计算

由麦克斯韦张量法可确定次级所受到的推力及悬浮力，即

式中:L为电机长度;D为电机宽度;n为磁场谐波次数。

次级的涡流损耗为

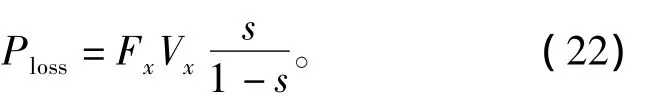
式中，Vx=2τf(1-s)为电机推进速度。

3 实验平台及特性分析

3.1 实验平台及参数设计

本直线感应电机实验平台主要包括直线电机本身与车载系统、数据采集系统、控制系统3部分。直线电机安放在轮轨车辆底部，与实验台板上拼接布置的非磁性感应板相对。车辆可沿轨道行走。通过调节的车体悬挂上的螺栓，可以调节气隙大小。推力可通过安装在车后部的传感器1测得。悬浮力可通过车体上传感器2、传感器3协同测得。非磁性次级直线电机极数为 4，极距为42 mm，槽宽为11 mm，槽高为 28.72 mm，轭部高为 25.78 mm，铁心宽度为 11 mm，绕组匝数为 150，次级铝板厚为15 mm，气隙在1～20 mm范围内调整。电机工作电压为380 V，最大电流为8 A。

图3 直线感应电机实验平台Fig.3 Photo of experimentation vehicle

3.2 理论计算及实验验证

利用式(20)～式(22)可计算出电机的推力、悬浮力及次级涡流损耗，并利用Ansoft有限元软件及实验平台进行有限元分析及实验验证。

图4为不同幅值下电机可产生的推力图。由图4可知，转差率为1时，电流幅值在4 A、6 A和8 A的条件下，电机推力随着电源频率先增大后减小。在20～40 Hz之间可达到最大值。由此可见，电机在低频段可输出较大推力。

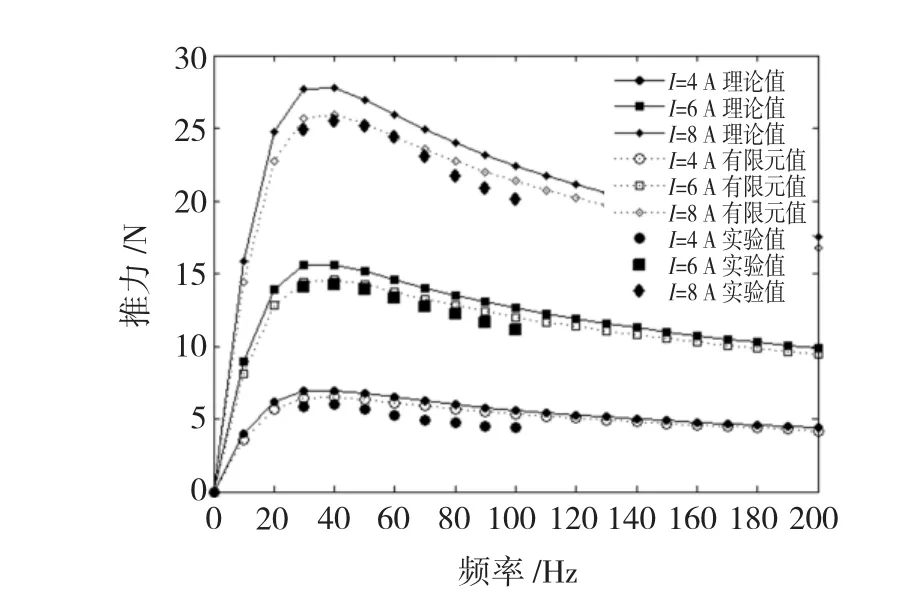
图4 不同电流幅值下的推力Fig.4 Thrust force curve under different current

图5为在电流幅值恒定，不同频率的条件下，电机的推力与转差率之间的关系。由图5可知，电机的推力随转差率先增大后减小。在120 Hz条件下，推力最大值出现在转差率为0.2～0.3之间。而在30 Hz条件下，推力最大值出现在转差率为0.6～1之间。

图5 不同转差率下的推力Fig.5 Thrust force curve under different slip

图6为考察电流分别在4 A、6 A及8 A条件下，不同频率电机输出悬浮力特性。悬浮力与频率呈单调上升关系。当频率增加到100～140 Hz后，悬浮力增加趋势变缓。理论值、有限元值与实验值之间的平均误差分别为 7.2%和 4.3%，均满足工程需要。

图6 不同电流幅值下的悬浮力曲线Fig.6 Levitation force curve under different current

图7为不同转差率时悬浮力变化曲线。由图7可知，在电流幅值恒定，不同频率的条件下，电机的悬浮力随转差率单调增加。在转差率为1时(堵转时)达到最大值。

图7 不同转差率下的悬浮力Fig.7 Levitation force curve under different slip

图8为电流幅值0～8 A，频率0～200 Hz范围内次级涡流损耗三维特性曲线。由图8可知，电机次级涡流损耗随电流幅值呈平方关系快速增加;随频率增加单调增加，但在高频段增加趋势放缓。次级损耗随频率变化趋势与悬浮力随频率变化趋势十分接近，这是由于悬浮力主要由次级内部涡流磁场产生。此结果与文献［14］结论相似。图9为不同转差率下，次级涡流损耗变化曲线。由图9可知，次级涡流损耗随转差率单调递增。当转差率小于0.3时，即高速运行时，涡流损耗增加较为平缓;当转差大于0.3时，损耗增加速度要明显加快，最大值出现在转差率为1附近。此外，高频条件下的涡流损耗远大于低频段的损耗。这说明单从损耗方面考虑，该类电机应工作在中高速范围内，这样可以有效降低次级损耗，提高工作效率。因此，在实际应用中，根据不同工况应找出合适的工作点，如在中低速工况下，可选择低频大电流条件，此时既可实现较大推力和一定的悬浮力，而次级涡流损耗相对较小。

图8 不同电流幅值、频率下的次级涡流损耗曲线Fig.8 Eddy loss curve under different current and frequency

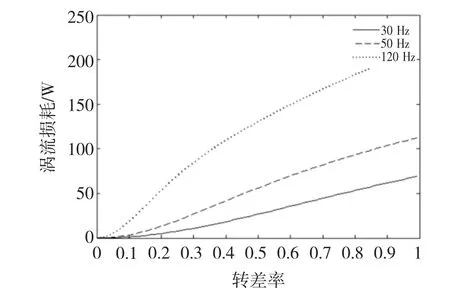
图9 不同转差率下的次级损耗Fig.9 Eddy loss curve under different slip

4 结语

本文研究了非磁性次级直线感应电机的基本原理，以麦克斯韦电磁方程为基础，建立了直线感应电机的简化二维电磁模型，并对其磁场进行了分析，得到了该电机的推进力、悬浮力及次级涡流损耗的解析表达式。非磁性次级直线感应电机与常规复合次级直线感应电机相比，其法向力表现为悬浮力，这样在实际运行中，可以减轻车体有效重量，提高运载能力。在输入电流一定的条件下，若以输出推力、效率为目标，电机应工作在低频段;若以输出悬浮力为目标，电机应工作在高频段。

［1］ YAN Luguang.Development and application of the magnet technology in China［C］//MT 15 Conference，Beijing，October.1997.

［2］ CHEN Yaowming，FAN Shuyuan，LU Wieshin.Electromagneticforce analysis of the magnetically levitated motor with two directions of movement［J］.IEEE Transactions on Industry Applications，2006，42(1):31-41.

［3］ BIRD Jonathan，LIPO Thomas A.A 3-D magnetic charge finiteelement model of an electrodynamic wheel［J］.IEEE Transactions on Magnetics，2008，44(2):253-265.

［4］ BIRD Jonathan，LIPO Thomas A.Characteristics of an electrodynamic wheel using a 2-D steady-state model［J］.IEEE Transactions on Magnetics，2007，43(8):3395-3405.

［5］ FUJII N，OGAWA K，CHIDA M.Three dimensional force of magnet wheel with revolving permanent magnets［J］.IEEE Transactions on Magnetics，1997，33(5):4221-4223.

［6］ FUJII N，NONAKA S，HAYASH G.Design of magnet wheel integrated own drive［J］.IEEE Transactions on Magnetics，1999，35(5):4013-4015.

［7］ 张广溢.直线电机静态横向边端效应研究［J］.电机与控制学报，1999，3(2):126-128.

ZHANG Guangyi.Research on the static transverse end effect of the linear motor［J］.Electric Machines and Control，1999，3(2):126-128.

［8］ 朱熙，范瑜，吕刚，等.单边盘式感应电机的数学模型与转矩分析［J］.中国电机工程学报，2010，30(24):69-74.

ZHU Xi，FAN Yu，LÜ Gang，et al.Modeling and torque analysis of a disc induction motor［J］.Proceedings of the CSEE，2010，30(24):69-74.

［9］ 朱熙，范瑜，李硕，等.旋转磁场电动式磁悬浮装置的状态方程与悬浮力控制［J］.电工技术学报.2011，26(12):1-6.

ZHU Xi，FAN Yu，LI Shuo，et al.State equations and lift force control of rotating field electrodynamic levitation device［J］.Transactions of China Electrotechnical Society，2011，26(12):1-6.

［10］ 秦伟，范瑜，吕刚，等.非磁性次级感应悬浮电机磁场和力特性研究［J］.电机与控制学报，2011，15(8):1-6.

QIN Wei，FAN Yu，LÜ Gang，et al.Characteristic and magnetic field analysis non-magnetic secondary induction maglev motor［J］.Electric Machines and Control，2011，15(8):1-6.

［11］ LI Shuo，FAN Yu，ZHU Xi，et al.New structure of axial flux induction motor and characterization analysis［C］//2011 International Conference on Electrical Machines and Systems，August 20-23，2011，Beijing，China.2011:6073906.

［12］ SUN Yanhua，YU Lie.Eddy current effects on radial active magnetic bearings with solid rotor［C］//8th International Symposium on Magnetic Bearing，August 26-28，2003，Mito，Japan，2003.

［13］ SUN Yanhua，YU Lie.Analytical method for eddy current loss in laminated rotors with magnetic bearings［J］.IEEE Transactions on Magnetics，2002，38(2):1341-1347.

［14］ 朱熙，范瑜，秦伟，等.旋转磁场电动式磁悬浮装置的力和损耗特性分析［J］.中国电机工程学报，2012，35(12):90-96.

ZHU Xi，FAN Yu，QIN Wei，et al.Force and loss characteristic analysis of rotating field electro-dynamic levitation devices［J］.Proceedings of the CSEE，2012，35(12):90-96.

［15］ 李硕，范瑜，朱熙，等.轴向磁通悬浮感应电机的特性研究与实验［J］.电工技术学报，2012，27(9):204-209.

LI Shuo，FAN Yu，ZHU Xi，et al.Characteristics of an axial flux induction maglev motor and experiment［J］.Transactions of China Electrotechnical Society，2012，27(9):204-209.