一种新的模糊聚类有效性指标

汤官宝

(阿坝师范高等专科学校基础教育系，四川 汶川 623002)

0 引言

聚类分析属于无监督模式识别的一个重要分支，基于一定的划分准则，它将待分类样本集划分为若干类，使得属于同一类的样本相似度尽量高，而不同类的样本相异性尽量大[1-2]。模糊C-均值算法(FCM)由于其具有简单、高效、数据适应性强等特点，是聚类分析中使用频率较高、较为流行的算法。如何建立合适的聚类评价标准来验证FCM算法最终的聚类结果的优劣是聚类分析的核心问题之一。为此许多学者做了大量研究工作。Zadeh给出第一个聚类有效性指标:分离度指标[3]，但判决效果并不理想。Bezdek提出了划分系数(PC)和划分熵(PE)的概念[4-5]。Dave[6]提出了改进的划分系数(MPC)。PC，PE，MPC这3项指标虽然具有直观的几何解释和良好的数学性质，但是它们的单调趋势以及与数据集本身缺少直接联系，限制了其应用。考虑数据集自身的信息，基于不同的类内紧致性和类间分离性函数，研究者又提出了一系列聚类有效性指标:Xie和Beni[7]提出了紧致分离指标VXB;Zahid和Limouri提出了VSC聚类有效性指标[8];Pakhira等提出VPBM聚类有效性指标和VPBMF聚类有效性指标[9-10];孔攀等提出了VN(c)聚类有效性指标[11]。数据类型和数据结构的多样化导致没有通用的模糊聚类有效性函数，从而导致有效性函数不断涌现[12-14]。充分考虑数据集的几何结构，本文基于内间分离性与类内紧致性的比值，提出一种新的模糊聚类有效性指标。该指标能够有效地确定由模糊C-均值算法(FCM)所得模糊划分的最优划分和最优聚类数。

1 模糊C-均值聚类算法

假定数据样本集合 X={x1，x2，…，xn}，模糊聚类是将X 划分为 c类(2≤c＜n)的过程，V={v1，v2，…，vc}为聚类中心。在模糊划分中，每个元素以一定隶属度属于某一类，uij表示第j个元素属于第i类的隶属度FCM的目标函数表示为:

其中:dik=‖xk－vi‖为样本点xk与聚类中心vi间的距离;m≥1为模糊加权指数[15]，通常取 m=2。FCM的算法思想是迭代调整(U，V)，使式(1)达到最小值。U，V迭代调整的过程由下面2个式子确定:

FCM聚类算法实施步骤如下:

步骤1 初始化各个参数，设定算法终止阈值。

步骤2 利用式(3)计算划分矩阵。

步骤3 利用式(2)更新聚类中心。

步骤4 如果达到终止条件，算法停止，得到划分矩阵和聚类中心。否则，转向步骤2。

2 新的有效性指标

充分考虑数据集的几何结构，用内间分离性与类内紧致性度量的比值作为聚类有效性标准是一种较好的方法。如何定义紧致性和分离性函数是本文关注的问题。本文定义的紧致性和分离性函数充分考虑数据集自身信息和它的几何结构，故能够有效地确定由模糊C-均值算法(FCM)所得模糊划分的最优划分和最优聚类数，具有较好的性能。

2.1 类内紧致性度量

定义类内紧致性度量函数c(c)为:

2.2 类间分离度度量

定义类间分离度度量函数s(c)为:

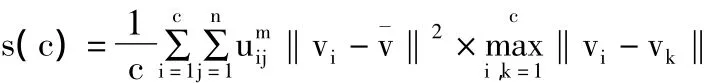
2.3 新的有效性指标

根据类间分离性度量和类内紧致性度量，本文定义新的聚类有效性指标:

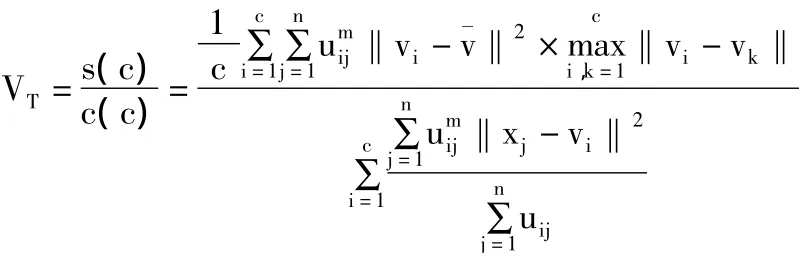
一个好的聚类结果要求较大的分离性，同时要求较小的紧致性。VT定义为分离性度量与紧致性度量之比。所以VT值越大，对应的聚类划分越好。通过求VT的值来确定最佳聚类数，其过程如下:

1)初始化参数[16]，设定c的搜索范围为2到。

2)for c=2 to cmax

①执行FCM算法;

②计算VT的值;

End。

3)找到最大的VT，对应的c即为最佳聚类数，对应的划分为最优划分。

3 仿真实验结果及分析

为了验证新的聚类有效性指标的性能，在1个人造数据集Data Set(1)和4个真实数据集(Iris、Wine、WBCD、WDBC)上进行测试，并和其它几类聚类有效性指标进行比较。FCM聚类算法最大迭代次数设定为100，最大类别数设为10，模糊指数m设为2。

3.1 数据集描述

人造数据集:Data Set(1)是二维平面上随机生成的数据集，共4类，每类50个样本。如图1所示。

图1 Data Set(1)数据集

真实数据集:采用UCI机器学习库中4个数据集，分别为 Iris、Wine、WBCD、WDBC 数据集[17]。表 1是对4个数据集的简单描述。

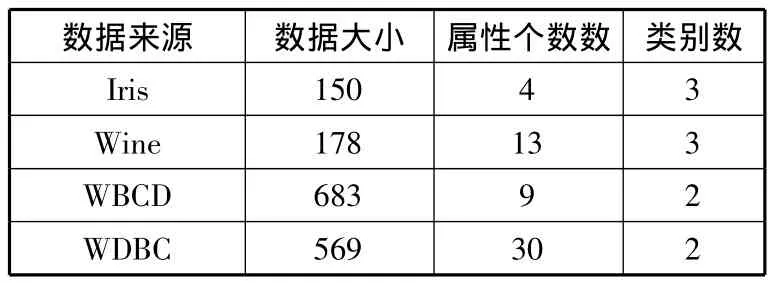
表1 数据集的简单描述

3.2 仿真实验结果

在上述5个数据集上运行FCM聚类算法，同时用本文提出的聚类有效性指标VT确定最佳聚类数。实验结果显示:VT指标确定5个数据集(Data Set(1)、Iris、Wine、WBCD、WDBC)的最佳聚类数分别为4、3、3、2、2，这与数据集的真实信息是相符的，从而说明聚类有效性指标VT具有良好的性能。

图2～图6为5个数据集上的有效性指标与聚类数之间的变化关系。

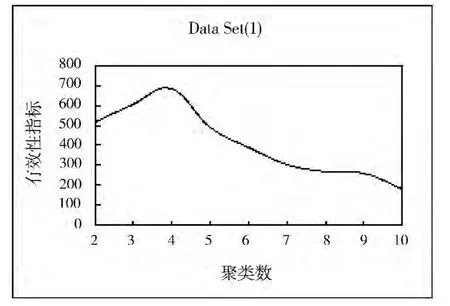
图2 Data Set(1)有效性指标与聚类数关系图

图3 Iris有效性指标与聚类数关系图

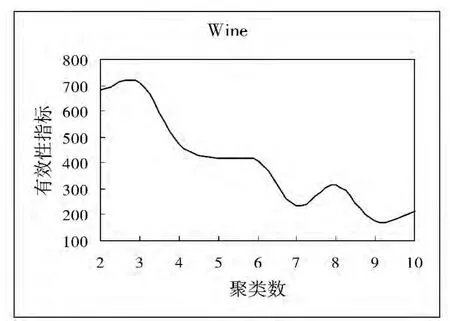
图4 Wine有效性指标与聚类数关系图

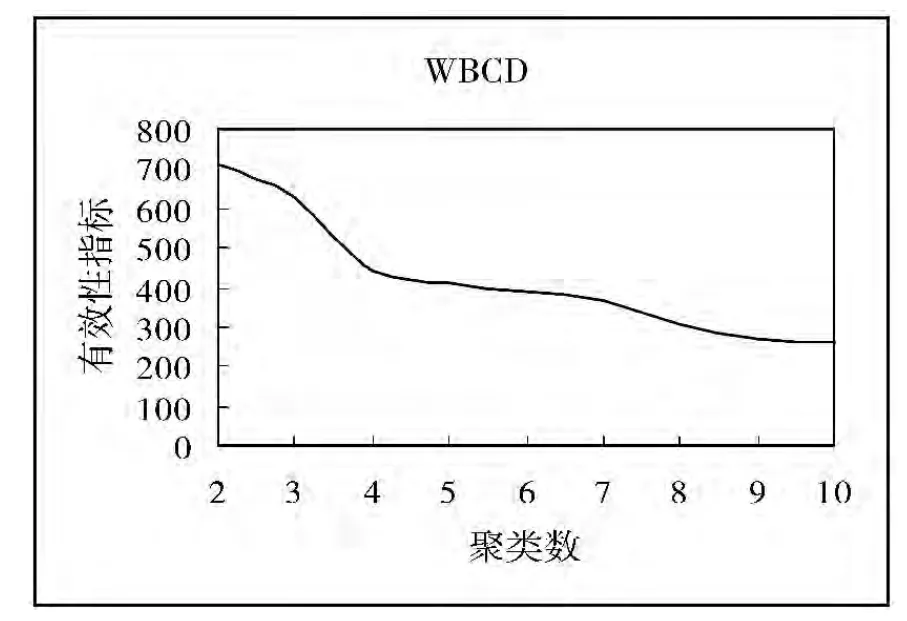
图5 WBCD有效性指标与聚类数关系图

图6 WDBC有效性指标与聚类数关系图

用多个聚类有效性指标确定4个真实数据集的最佳聚类数，结果如表2所示。从表2可以看出，只有VPBMF，VN，VT这3项指标确定的最佳聚类数与所有4个数据集的真实信息相符，说明VT聚类有效性指标是优于多个现有聚类有效性指标的。

表2 多种有效性指标确定的最佳聚类数对比

4 结束语

当数据集的聚类数未知时，有效性指标可以用来确定最佳聚类数。本文提出的基于类内紧致性和内间分离性的聚类有效性指标，可以有效确定最佳聚类数和最优划分。实验结果表明其具有良好的性能。

[1] 高新波，谢维信.模糊聚类理论发展及应用的研究进展[J].科学通报，1999，44(21):2241-2251.

[2] 高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社，2004.

[3] Zadeh L A.Similarity relations and fuzzy orderings[J].Information Science，1971，3(2):177-200.

[4] Bezdek J C.Cluster validity with fuzzy sets[J].Journal of Cybernetics，1974，3(3):58-73.

[5] Bezdek J C.Numerical taxonomy with fuzzy sets[J].Journal of Mathematical Biology，1974，1(1):57-71.

[6] Dave R N.Validating fuzzy partitions obtained through cshells clustering[J].Pattern Recognition Letters，1996，17(6):613-623.

[7] Xie X L，Beni G.A validity measure for fuzzy clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1991，13(8):841-847.

[8] Zahid N，Limouri M，Essaid A.A new cluster-validity for fuzzy clustering[J].Pattern Recognition，1999，32(7):1089-1097.

[9] Pakhira M K，Bandyopadyay S，Maulik U.Validity index for crisp and fuzzy clusters[J].Pattern Recognition，2004，37(3):487-501.

[10] Pakhira M K，Bandyopadyay S，Maulik U.A study of some fuzzy cluster validity indices，genetic clustering and application to pixel classification[J].Fuzzy Sets and Systems，2005，155(2):191-214.

[11] 孔攀，邓辉文，黄艳艳，等.一个新的模糊聚类有效性指标[J].计算机工程，2009，35(12):143-144.

[12] Rezaee B.A cluster validity index for fuzzy clustering[J].Fuzzy Sets and Systems，2010，161(23):3014-3025.

[13] Le Capitaine H，Frelicot C.A cluster-validity index combining an overlap measure and a separation measure based on fuzzy-aggregation operators[J].IEEE Transactions on Fuzzy System，2011，19(3):580-588.

[14] Kwon S H.Cluster validity index for fuzzy clustering[J].Electronics Letters，1998，34(22):2176-2177.

[15] Pal N R，Bezdek J C.On cluster validity for the fuzzy cmeans model[J].IEEE Transactions on Fuzzy Systems，1995，3(3):370-379.

[16] 于剑，程乾生.模糊聚类方法中的最佳聚类数的搜索范围[J].中国科学(E 辑)，2002，32(2):274-280.

[17] UCI.Fuzzy Clustering[EB/OL].http://www.ics.uci.edu/mlearn/MLRepository.html，2014-03-05.