对流扩散方程数值耗散的定量研究方法
崔 冬,何小燕,杨海燕
(1.上海市水利工程设计研究院有限公司,上海 200061;2.上海围海工程技术研究中心,上海 200061)
对流扩散方程数值耗散的定量研究方法
崔 冬1,2,何小燕1,2,杨海燕1,2
(1.上海市水利工程设计研究院有限公司,上海 200061;2.上海围海工程技术研究中心,上海 200061)
针对对流扩散方程数值耗散问题普遍缺乏明确定量指标的现状,提出了度量数值耗散程度的定量指标及其研究方法,即借助广义“假扩散”系数这一定量指标来度量某一离散格式的数值耗散程度,其数值上近似等于具有相同扩散效应的真扩散所对应的扩散系数,其中真扩散效应可通过求解纯扩散问题的高精度数值解近似得到。采用该方法研究了三阶QUICKEST离散格式的数值耗散规律,分析了时间步长、流速大小及空间步长对“假扩散”系数的敏感性以及相关性,得到了“假扩散”系数的具体表达式,进而验证了该定量研究方法的可行性。
对流扩散方程;数值耗散;QUICKEST离散格式;流体力学
保守性物质的对流扩散是流体力学、环境科学领域中经常遇到的一类经典问题,可用对流扩散方程加以描述,如式(1)所示。该方程由非恒定项对流项u扩散项组成,一般采用数值离散的方法求解,但求解过程中不可避免地会带来一定的离散误差而影响数值解的准确性,其中影响较大的离散误差是由一阶导数项(非恒定项、对流项)离散带来的数值耗散[1]。数值耗散,也称“假扩散”,是截断误差的一种,会放大扩散作用的效应,是对流扩散方程数值求解中普遍存在的一个问题,且数值耗散程度越大,给数值解带来的计算误差越大。在应用某种研究手段研究实际对流扩散问题之前,有必要对研究手段的数值耗散程度有较为准确的把握,以便判断研究手段的适用性,并尽可能地减小这种“假扩散”效应[2]。

式中:c为物质的质量浓度;t为时间;x、y为直角坐标系坐标;u、v分别为沿x、y方向的流速;Dx、Dy分别为物质沿x、y方向的扩散系数。当u=v=0时,式(1)可简化为纯扩散方程;当Dx=Dy=0时,式(1)可简化为纯对流方程。
对流扩散方程求解存在的数值耗散问题,一直受到研究人员的关注,并已取得了诸多研究成果[1-9],如提出了改进离散格式、减小空间步长等减少“假扩散”效应的措施。但针对不同离散格式以及同一离散格式不同参数下的数值耗散程度尚缺乏统一的度量指标,已有的研究往往是通过比较经典算例数值解与解析解的差异程度、纯对流问题数值解最大浓度随时间的降低程度等间接方式来判断数值耗散程度的大小,这给实际应用带来不便。针对当前研究现状,本文提出度量数值耗散程度的定量指标及研究方法,并将该方法应用到三阶QUICKEST离散格式的数值耗散规律的研究中,以进一步验证方法的可行性。
1 定量指标的提出
数值耗散最早定义为对流扩散方程中一阶导数项(非恒定项、对流项)离散格式的截断误差小于二阶而引起较大数值计算误差的现象。以二维纯对流方程为例,当采用一阶迎风格式对非恒定项和对流项进行数值离散时,略去三阶及三阶以上的项,其等价表达式[10]为

式中:等号后两项即为数值离散引入的数值耗散项; Δx、Δy分别为沿x、y方向的空间步长;Δt为时间步长。将分别定义为沿x、y方向的“假扩散”系数,形式上起扩散系数的作用。
事实上“假扩散”效应不仅存在于一阶离散格式中,其他离散格式中也存在,如二阶迎风格式、三阶迎风格式、QUICK格式等[11]。参照式(2),设想其他离散格式下二维纯对流方程也可写成类似的等价表达式:

将Dfalse定义为广义的“假扩散”系数,用来定量表征数值耗散程度,这样就可将“假扩散”系数这一重要参数的应用范围由一阶迎风离散格式推广到更多离散格式中。
2 定量指标的研究方法
2.1 研究方法的提出
由于数值离散的复杂性,很多离散格式难以直接写出“假扩散”系数的表达式。考虑到“假扩散”对数值解的影响表现为放大了扩散效应,“假扩散”应与真扩散具有类似的扩散效应,若能找到与“假扩散”效应相当的真扩散,则可以认为二者具有相同的扩散系数。即“假扩散”系数取值上近似等于具有相同扩散效应的真扩散对应的扩散系数,其中不同扩散系数下的真扩散效应,可以通过求解纯扩散方程的高精度数值解近似得到。
以下拟采用沿单一方向(x方向)的纯对流问题来研究“假扩散”效应,这样既消除了物质自身扩散带来的影响[6],又将二维问题简化为一维,式(3)可简化为式(4);相应地,采用单一方向(x方向)的纯扩散问题来模拟真扩散效应,如式(5)所示,可消除对流项离散带来的计算误差。

计算模型设置如下:计算区域为一个长100km、宽8 km、水深10 m的河道,计算网格采用单一矩形网格,网格走向与河道走向一致。当采用纯对流问题研究“假扩散”效应时,初始时刻设置一个1 km× 1 km范围、初始质量浓度为20 mg/L的保守性物质团位于河道上游,其他计算区域初始浓度为零,水体沿河道纵向均匀流动,如图1所示。当采用纯扩散问题研究真扩散效应时,计算网格空间步长经试算取25 m可达到足够精度,水体静止,初始时刻设置1 km×1 km范围、初始质量浓度为20 mg/L的保守性物质团位于河道中游,如图2所示。

图1 纯对流问题下计算模型及初始浓度设置

图2 纯扩散问题下计算模型及初始浓度设置
2.2 基本假定的验证
本文提出的“假扩散”系数的研究方法有一个基本假定,即认为当真扩散与“假扩散”具有相同扩散效应时,二者应当具有相同的扩散系数;反过来说,当二者具有相同扩散系数时,二者应当具有相同的扩散效应。为了验证这一基本假定的正确性,以下采用“假扩散”系数具有理论解的一阶迎风离散格式来模拟“假扩散”效应,与具有相同扩散系数的真扩散效应进行对比,观察二者是否相近。参数设置及一阶迎风离散格式的“假扩散”系数理论解(根据式(2)计算得到)如表1所示。

表1 一阶迎风离散格式不同参数下的“假扩散”系数理论解
采用具有一阶迎风格式的MIKE 21对流扩散模型[12]求解如图1所示的纯对流问题,可分别得到2组参数下在时间t=6 h时的“假扩散”效应如图3所示(截图范围以浓度团为中心,沿河道纵向与横向分别取10 km与4 km)。

图3 一阶迎风离散格式下的“假扩散”效应(t=6 h,单位:mg/L)
真扩散效应通过求解图2所示的纯扩散问题的高精度数值解近似得到,其中非恒定项采用一阶迎风格式离散,扩散项采用二阶中心差分格式离散,对大多数有实际意义的问题,二者的离散精度已能满足需要[1]。表1所示的2组扩散系数对应的t=6 h时真扩散效应如图4所示。对比图3与图4可以看出,“假扩散”与真扩散呈现出几乎完全一致的扩散效应。这说明当真扩散与“假扩散”具有相同扩散系数时,二者具有相同扩散效应的基本假定是成立的;反过来说,当真扩散与“假扩散”具有相同扩散效应时,二者具有相同扩散系数的基本假定也是成立的。
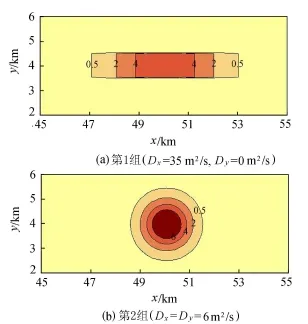
图4 纯扩散问题下的真扩散效应(t=6 h,单位:mg/L)
2.3 纯扩散问题的高精度数值解
通过求解图2所示的纯扩散问题的高精度数值解,近似得到单一方向(x方向)扩散系数取值为0~50 m2/s之间的浓度场分布情况,其中部分取值下的浓度场纵断面分布如图5所示。为方便实际应用,本文根据图5呈现的浓度场纵断面分布特征,并参考以往研究成果,选用物质团在静水中扩散6 h与12h后对应的扩散范围(以0.5mg/L包络范围来统计扩散范围)与最大浓度值来表征不同扩散系数下的扩散效应,如图6所示。当研究某种离散格式数值耗散程度时,可采用相应的离散格式求解图1所示的纯对流问题,统计得到t=6 h与t=12 h的物质团扩散范围与最大浓度值,通过查图6,找到相对应的“假扩散”系数。

图5 部分扩散系数下的浓度场纵断面分布

图6 扩散系数与物质团扩散范围及最大浓度值的关系
此外,通过图5、图6还可以看出,扩散作用的存在使保守性物质团最大浓度值降低程度明显,当扩散系数分别取5 m2/s与30 m2/s时,经过6 h单一方向的扩散,物质团最大浓度分别由20 mg/L降低至14.6mg/L与6.95mg/L,降低幅度分别为27%与65%。
3 研究方法的初步应用
以下以三阶QUICKEST离散格式为例介绍度量数值耗散程度的定量方法在研究某一离散格式下数值耗散规律中的应用,三阶QUICKEST格式由广泛应用于一维数值模拟的二次迎风插值格式——QUICK格式演变而来,三阶QUICKEST格式在QUICK格式的基础上加以改进,将应用范围扩展至多维[3]。利用当前节点值、上游最近的2个节点值、下游最近的1个节点值等10个节点共同构造差分[3](式(6)),表达式复杂,难以直接确定“假扩散”系数。

式中:n为时间步长的编号;j为节点沿x方向的编号;k为节点沿y方向的编号;A1~A10为系数。
由式(2)可知,“假扩散”系数一般与时间步长、流速大小、空间步长有关。为了得到三阶QUICKEST离散格式的数值耗散规律,分别研究了时间步长、流速大小、空间步长对“假扩散”系数的敏感性以及相关性。
3.1 时间步长的敏感性及相关性
采用三阶QUICKEST离散格式分别研究了Δx =100 m、200 m两组空间步长(流速以0.5 m/s为例)下的“假扩散”效应,通过查图6可以得到相对应的“假扩散”系数,如图7所示。可以看出,时间步长对“假扩散”系数不敏感,改变时间步长,“假扩散”系数几乎不受影响(理论上改变时间步长会对舍入误差略有影响,因而造成计算结果之间的微小差异)。

图7 三阶QUICKEST离散格式下时间步长对“假扩散”系数的敏感性
3.2 流速大小的敏感性及相关性
采用三阶QUICKEST离散格式分别研究了100m、200m两组空间步长下流速大小取0.1~2 m/s时对应的“假扩散”效应,通过查图6可以得到相对应的“假扩散”系数如图8所示。可以看出,流速大小对“假扩散”系数敏感,改变流速大小,“假扩散”系数会随之变化。采用趋势线拟合发现,三阶QUICKEST离散格式下“假扩散”系数与流速的0.5次方呈相当好的拟合关系。

图8 三阶QUICKEST离散格式下“假扩散”系数与流速大小的相关关系
3.3 空间步长的敏感性及相关性
采用三阶QUICKEST离散格式分别研究了0.5 m/s、2m/s两组流速下空间步长取25~500m时的“假扩散”效应,通过查图6可以得到相对应的“假扩散”系数如图9所示。可以看出,空间步长对“假扩散”系数相当敏感,改变空间步长,“假扩散”系数会发生较大变化。采用趋势线拟合发现,三阶QUICKEST离散格式下“假扩散”系数与空间步长的2次方呈相当好的拟合关系。

图9 三阶QUICKEST离散格式下“假扩散”系数与空间步长的相关关系
3.4 “假扩散”系数的表达式
由图8、图9可以看出,三阶QUICKEST离散格式下的“假扩散”系数与流速的0.5次方及空间步长的2次方呈正相关关系。因此,认为三阶QUICKEST离散格式下“假扩散”系数可写成

式中η为系数,可由图8及图9的拟合关系推求得到。以图8为例,当空间步长为100m时,由Dfalse(x)= ηu1/2Δx2=1002u1/2η=0.75u1/2,可 推 求 出η=7.5×10-5。由图9亦可得到η=7.5×10-5。因此三阶QUICKEST离散格式下“假扩散”系数表达式可写为

4 结 论
a.可借助广义“假扩散”系数这一定量指标来度量某一离散格式的数值耗散程度,“假扩散”系数数值上近似等于具有相同扩散效应的真扩散所对应的扩散系数,其中真扩散效应可通过求解纯扩散问题的高精度数值解近似得到。
b.采用该定量研究方法,成功得到了三阶QUICKEST离散格式的数值耗散规律,验证了该定量研究方法的可行性。
[1]陶文铨.计算传热学的近代进展[M].北京:科学出版社,2000:105-154.
[2]杨屹松,李炜.混合有限分析格式的数值耗散及频散[J].水利学报,1992,22(10):26-31.(YANG Yisong,LI Wei.Numerical dissipation and dispersion of hybrid finite analytic method[J].Journal of Hydraulic Engineering, 1992,22(10):26-31.(in Chinese))
[3]EKEBJARG L,JUSTSEN P.An explicit scheme for advection-diffusion modeling in two dimensions[J]. ComputerMethodsinAppliedMechanicsand Engineering,1991,88(3):287-297.
[4]陈炳睿,朱建荣.物质输运方程中平流项数值格式的改进[J].华东师范大学学报:自然科学版,2006(4):64-70.(CHEN Bingrui,ZHU Jianrong.Numerical scheme improvement of the advection term in mass transport equation[J].Journal of East China Normal University: Natural Science,2006(4):64-70.(in Chinese))
[5]谢志华,林建国,由晓丹.污染物对流扩散方程的几种新的高阶QUICK组合显格式比较研究[J].水动力学研究与进展:A辑,2005,20(3):346-356.(XIE Zhihua, LIN Jianguo,YOU Xiaodan.Comparative investigation of some high-order explicit schemes combined with QUICK for the convection-diffusion equation of pollutants[J]. Chinese Journal of Hydrodynamics,2005,20(3):346-356.(in Chinese))
[6]程爱杰,赵卫东.对流扩散方程的经济差分格式[J].计算数学,2000,22(3):309-318.(CHENG Aijie,ZHAO Weidong.An economical difference scheme for convectiondiffusion equations[J].Mathematica Numerica Sinica, 2000,22(3):309-318.(in Chinese))
[7]林建国,殷佩海.污染浓度对流扩散的三节点高精度格式[J].大连海事大学学报,2002,28(4):64-67.(LIN Jianguo,YINPeihai.Three-pointschemewithhigh accuracy for the convection-diffusion equation of the pollutant concentration[J].Journal of Dalian Maritime University,2002,28(4):64-67.(in Chinese))
[8]由同顺.非线性对流-扩散方程的高阶特征:差分格式及其误差估计[J].数值计算与计算机应用,1994(4): 312-317.(YOUTongshun.High-ordercharacteristicdifference schemes for the nonlinear convection:diffusion equation andtheirerrorestimates[J].Journalon Numerical Methods and Computer Applications,1994(4): 312-317.(in Chinese))
[9]卢洪波,谢鸿罡,杨沫,等.一种改进的QUICK差分方案[J].东北电力学院学报,1998,18(4):1-6.(LU Hongbo,XIE Honggang,YANG Mo,et al.A modified numerical method with QUICK scheme[J].Journal of Northeast China Institute of Electric Power Engineering, 1998,18(4):1-6.(in Chinese))
[10]汪德爟.计算水力学理论与应用[M].南京:河海大学出版社,1989:117-118.
[11]胡洪,黄虎,宋倩倩,等.不同对项离散格式对流场计算的影响[J].数值计算与计算机应用,2010,31(2):153-160.(HU Hong,HUANG Hu,SONG Qianqian,et al.The influence of different discrete scheme of the convective term on term on fluid field calculation[J].Journal on Numerical Methods and Computer Applications,2010,31 (2):153-160.(in Chinese))
[12]许婷.丹麦MIKE21模型概述及应用实例[J].水利科技与经济,2010,16(4):867-869.(XU Ting.Calculation principle and application example of a two-dimensional flow model:MIKE21 HD[J].Water Conservancy Science and Technology and Economy,2010,16(4):867-869.(in Chinese))
Quantitative research method of numerical dissipation levels of convective-diffusive equation//
CUI Dong1,2,HE Xiaoyan1,2,YANG Haiyan1,2
(1.Shanghai Water Engineering Design and Research Institute Co.,Ltd.,Shanghai 200061, China;2.Shanghai Engineering Research Center of Reclamation,Shanghai 200061,China)
Considering the fact that quantitative indicator on numerical dissipation is lacking,in this paper the quantitative indicator and research method were given.The method is,namely,using generalized“false diffusive”coefficient of the certain indicators to measure the degree of numerical dissipation of a discrete format.The numerical value of the above method approximately equals to the same effect on the true diffusion of the diffusion coefficient.As to the true diffusion effect,the highly precise numerical value can be approximately obtained by the solution of the pure diffusion formulas.This method was successfully applied to third-order QUICKEST discrete scheme.The overall results show that false diffusion coefficient could be introduced to characterize the numerical dissipation level,whose value can be obtained by comparing the true diffusion effect.
convective-diffusive;numerical dissipation;QUICKEST discrete scheme;fluid mechanics
TV131.2;O241.82
:A
:1006-7647(2014)05-0008-04
10.3880/j.issn.1006-7647.2014.05.002
201309-18 编辑:骆超)
上海市科学技术委员会资助课题(13DZ2251500)
崔冬(1982—),女,江苏徐州人,工程师,硕士,主要从事河口海岸工程研究。E-mail:njcuidong.student@sina.com

