不确定条件下的下辽河平原地下水本质脆弱性评价

孙才志,奚 旭

(辽宁师范大学城市与环境学院,辽宁大连 116029)

不确定条件下的下辽河平原地下水本质脆弱性评价

孙才志,奚 旭

(辽宁师范大学城市与环境学院,辽宁大连 116029)

针对地下水系统中水文地质参数的随机性和模糊性会对地下水脆弱性评价结果产生较大误差问题,在辨析参数不确定性特点基础上,利用蒙特卡罗法同时对随机性参数和模糊性参数赋值,并结合DRASTIC模型对下辽河平原的地下水本质脆弱性进行评价。通过模拟计算出模糊性参数在不同α截集水平下地下水脆弱性指数不同可能性下的累积分布曲线,得到不同保证率、不同可能性情况下地下水脆弱性指数的隶属函数,并从脆弱性和不确定性两个角度对各分区地下水脆弱性进行对比分析。分析结果表明:Ⅰ1区脆弱性程度相对最高,不确定性程度一般;Ⅰ2、Ⅰ3、Ⅱ1和Ⅱ3区的脆弱性程度较高,且Ⅰ2、Ⅰ3区的不确定性程度相对最高,Ⅱ1和Ⅱ3区的不确定性程度最低;Ⅰ4、Ⅱ2、Ⅲ和Ⅳ区的脆弱性程度相对较低,其中Ⅱ2和Ⅳ区的不确定性程度较低,Ⅰ4区的不确定性程度一般,Ⅲ区的不确定程度较高。较传统评价过程,本次地下水脆弱性评价综合参数的不确定性分析得出了不确定条件下地下水脆弱性的隶属函数,结果切合客观实际。

地下水本质脆弱性;水文地质;DRASTIC模型;不确定性;蒙特卡罗法;α截集;累积分布曲线;下辽河平原

自1968年Margat提出“地下水脆弱性”这一术语以来,其概念和研究方法不断得到丰富和发展[1-2]。地下水脆弱性研究是地下水保护的基础性工作,通过地下水脆弱性研究,可以区别不同地区地下水的脆弱性程度,评价地下水潜在易污染性,圈定地下水脆弱范围,从而警示人们在开采利用地下水资源的同时,采取有效的防治与保护措施。

近年来伴随GIS技术的应用,国内外在地下水脆弱性研究方面都取得了非常丰富的成果。由于地下水系统的复杂性,在地下水脆弱性评价过程中存在较多不确定性因素,如何利用所有可获取资料求得尽可能精确合理的评价结果是国内外学者的努力方向。在国外,许多学者[3-5]利用GIS技术叠加指标图层获取研究区地下水脆弱性分布图,该方法可以直观细致地体现研究区地下水脆弱性具体分布状况,但需要大量数据支持,结果仍存在一定误差; Rupert等学者[4,6-8]通过分析研究区硝酸盐氮和亚硝酸盐氮的实测资料,对DRASTIC模型的评价结果进行了校正,获取契合实情的地下水脆弱性分布图,该方法对农业区有较好的应用意义,但土壤中氮含量的数据资料收集较为困难,不具有普适性。我国学者在参考国外优秀案例的基础上,对评价方法进行了改进,陈守煜等[9]提出权重确定的十级语气算子,孟宪萌等[10]引入模糊集与信息熵理论,都丰富了DRASTIC模型中权重确定的理论;孙才志等[11-13]都曾运用模糊综合评价法,获取了较为细致精确的评价结果。通过多种方法结合建模可使地下水脆弱性评价更科学合理,然而数学方法并非万能工具,在评价模型中资料难以获取的情况下,需要放弃一些评价因子或用其他因子代替,付素蓉等[14]去掉了DRASTIC模型中的土壤类型和地形坡度,增加了含水层厚度;孙爱荣等[15]根据实际情况,用降雨入渗补给量代替地下水净补给量,在实际评价过程中都取得了较好的效果。

通过以上多种方法,可求得整体范围内较为科学合理的评价结果,然而不确定性因素是客观存在的,大多数学者在评价过程中均运用传统数学方法获取参数均值进行计算,这是与实际情况不符的,应该用适当方式体现地下水脆弱性中的不确定性。鉴于此,本研究用蒙特卡罗(Monte Carlo)法对随机性参数和模糊性参数进行模拟赋值,结合DRASTIC模型对下辽河平原地区进行地下水脆弱性评价,通过生成地下水脆弱性指数不同可能性下的累积分布曲线与地下水脆弱性指数的隶属函数图,获取客观合理的地下水脆弱性计算结果。相较传统研究方法,本次评价反映出了因参数空间变异性而导致评价结果的不确定性,用模糊隶属区间表示评价结果更切合实情,可以为决策者和管理者提供更准确的参考依据。

下辽河平原是辽宁省重要的工农业生产基地和经济发展中心,同时也是东北地区最缺水、地下水资源供需矛盾最突出的地区[16]。地下水作为该地区主要水源,面临过度开采以及污染严重等问题,对下辽河平原进行地下水本质脆弱性研究能够为该地区地下水资源的合理开发和利用提供科学的决策依据,对于当地可持续发展具有重大意义。

1 研究方法与数据来源

1.1 DRASTIC模型

DRASTIC模型是1985年由美国环境保护署(USEPA)提出的[17],它综合了40多位水文地质专家的经验,具有良好的科学适用性,在国内外应用都非常广泛。该方法选取了7个对地下水脆弱性影响比较大的指标:地下水位埋深D、净补给量R、含水层介质类型A、土壤介质类型S、地形坡度T、渗流区介质类型I以及含水层水力传导系数C,其中D、R、T、C是可以直接获取数据的定量指标,A、S、I为不可直接获取数据的定性指标。DRASTIC模型7个指标按其对地下水脆弱性的影响程度不同,分别被赋予固定权重值:5、4、3、2、1、5、3,可根据其相对数值计算出权重具体数值:0.217、0.174、0.131、0.087、0.043、0.217、0.131。每个指标根据其变化范围和其内在属性进行等级划分并给出脆弱性等级评分值,见表1和表2。

表1定量指标分级与评分

表2定性指标分级与评分

各指标的加权和就是地下水脆弱性指数VⅠ:式中:w为权重;r为评分值。

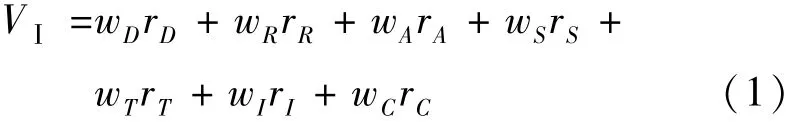
1.2 蒙特卡罗法

蒙特卡罗法是近几年来伴随计算机技术的发展而开始广泛使用的不确定性研究方法。它以概率统计理论为基础,依据大数定律,利用计算机模拟程序,解决一些很难用数学运算或其他方法求解的复杂问题,可以将以往只能定性研究的问题定量化。该方法在经济学、生物医学、物理学、水文学等领域应用广泛,具有独特的优越性和适用性。

蒙特卡罗法通过假设已知随机过程的概率分布函数,在已知样本的统计特征(平均值、标准差等)基础上,利用计算机模拟程序进行仿真实验,产生多组随机变量,再将随机变量代入模型,得到多组解的统计估计量,从而可以得出实验对象的某种规律或者问题的解,模拟次数足够多,就可以获得一个比较精确的值。蒙特卡罗法的关键步骤在于伪随机数的产生,常见的一维分布随机数有正态分布、指数分布、均匀分布、对数正态分布等,本文在参考前人研究的基础上并根据所获取参数数据的结构设定参数的概率分布函数。

1.3 数据来源

选取下辽河平原所跨市、县(区)的水文地质参数数据进行计算分析。数据来源于《辽宁省统计年鉴》《辽宁省水资源公报》《辽宁省国土资源地图集》《辽宁国土资源》《辽宁省水文地质图集》《辽宁省水资源》、DEM提取数据以及多年多测点实测数据等资料。

2 研究区概况与水文地质分区

2.1 研究区概况

下辽河平原位于辽河中下游地区,辽宁省的中部,东依千山山脉,西靠医巫间山,北部隔铁法波状丘陵与松辽平原相望,南临渤海的辽东湾。东西宽120～140 km,南北长240 km,面积约2.65万km2。平原地势由东西两侧向中部地区倾斜,自北向南逐渐低平,平均海拔低于50 m,是区域地表水和地下水的汇集中心,地下水总的径流方向趋同于地势,由山前向中部平原呈放射状,至中部平原后,总的径流方向是由东北向西南,最后进入辽东湾。在南部滨海地带,由于地势低洼,受潮汐和洪涝威胁,该地区土地盐渍化和沼泽化比较严重。行政区划隶属于辽宁省铁岭市、阜新市、沈阳市、抚顺市、辽阳市、鞍山市、营口市、盘锦市、锦州市,总跨9市22县(区),如图1所示。

2.2 水文地质分区

本次研究在下辽河平原地区已经形成的东部山前倾斜平原、西部山前倾斜平原、中部冲积平原和南部滨海平原4个水文地质单元基础上,按含水层成因和地下水补给来源不同进一步划分,将下辽河平原划分成9个地下水脆弱性评价基本单元(表3、图1)。

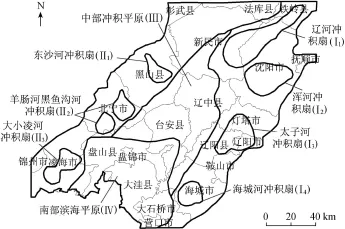
图1 下辽河平原地下水系统分区示意图

表3 下辽河平原地下水脆弱性评价分区

3 参数的不确定性分析

在地下水脆弱性评价过程中,存在诸多不确定性因素,如参数的时空变异性、评价体系中参数边界确定的模糊性、资料不足或历史累积资料的缺失等,这些不确定性因素容易使地下水脆弱性的评价结果与客观实际脱节。本研究在收集较多水文地质参数数据基础上,主要对两方面的不确定性因素进行处理:①地下水系统本身具有的不确定性,主要表现为水文地质参数的空间变异性;②评价结果的不确定性,表现为因参数的空间异质性而导致评价结果具有模糊性。在地下水脆弱性评价过程中综合了参数的不确定性分析,得出模糊性参数取不同可能性情况下地下水脆弱性指数的隶属函数,评价结果包括区域地下水脆弱性大小以及不确定性大小。具体实现过程包括以下步骤:①根据分析参数的不确定性类型,将参数分为随机性参数或模糊性参数,并表征各参数的不确定性特征;②模糊性参数取不同α截集,连同随机性参数一起进行足够多次的随机模拟,将模拟结果代入DRASTIC模型,可得不同α截集下地下水脆弱性指数的累积分布曲线;③各个分区内,多条地下水脆弱性累积分布曲线均取不同保证率,得到各分区的不同可能性——地下水脆弱性指数的隶属函数。

3.1 参数的不确定性分类与表征

3.1.1 随机性参数

水文地质参数D、R、T、C在不同地理位置点上的数值各不相同,具有明显的离散随机性,根据多测点数据,将它们进行随机性表征(表4)。研究表明一个变量如果受到大量微小、独立的随机因素影响,那么这个变量一般服从正态分布[18]。D的大小受地质、水文地质条件、土壤条件、开采强度等诸多因素影响,具有空间异质性;同样R受降水量、蒸腾、地形、植被等诸多微小、独立因素影响而存在变异性,这两个参数可视为正态分布。由于各研究分区内均为下辽河平原城镇地区,T变化偏差较小,且同一水文地质分区内具有连续性,本次研究将其视为均匀分布;对于参数C,此前多位学者研究表明一般呈现出对数正态分布[19-20],本次研究同样将其视为对数正态分布。

3.1.2 模糊性参数

同一水文地质分区内具有相同的地质形成背景,DRASTIC模型中3个定性指标A、S和I在同一分区内具有连续性和渐变性,即趋于同一类型,但在不同地理位置点上它们的类型不可能全部相同,因此这3个参数具有模糊性,呈三角分布。根据表2中的分级评分将各分区的A、S和I进行定量化,将定量化数据导入ArcGIS形成指标图层,对这3个指标图层中的每个研究分区创建2 km×2 km的正方形网格,并对网格中的数据进行提取,获取分区内所有网格点评分值,进行模糊化处理(表4)。

3.2 不确定性参数随机模拟

将表4中参数的不确定性特征值输入模拟程序,设定10 000次随机模拟,将每次模拟结果代入DRASTIC模型,每个分区可得到10000个地下水本质脆弱性评价结果:

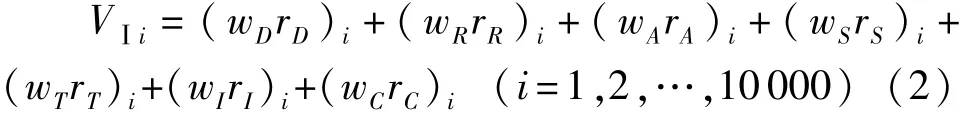
式中:wDrD、wRrR、wTrT和wCrC为随机变量;wArA、wSrS和wIrI为模糊变量。由于三角模糊数在一定区间内分布,模糊数取不同可能性,评价结果在一定区间内波动,通过取不同α截集,可得不同可能性下地下水脆弱性指数的累积分布曲线。在每个α截集下,三角模糊数具有下限值和上限值,可得地下水脆弱性指数在这一α截集下的下限分布和上限分布:

为反映不同可能性情况下脆弱性指数的不确定性,三角模糊数分别取α=0.5、α=0.6、α=0.7、α= 0.8、α=0.9和α=1时进行随机模拟。

4 模拟结果与地下水本质脆弱性分析

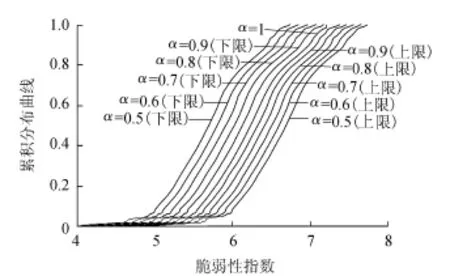
图2 辽河冲积扇地下水脆弱性指数不同可能性下的累积分布曲线

表4 地下水脆弱性参数的不确定性表征

模糊性参数取不同可能性,连同随机性参数一起进行蒙特卡罗模拟赋值,生成不同可能性下的累积分布曲线(图2,限于篇幅,本文仅以辽河冲积扇为例,其他分区图形类似),为保证结果的可靠性,在每个α截集下地下水脆弱性指数的累积分布曲线中取不同保证率,各分区可得地下水脆弱性指数在不同可能性下,取不同保证率的地下水脆弱性指数隶属区间(表5)与隶属度函数(图3)。

表5 不同α截集与不同保证率下地下水脆弱性指数的隶属区间

图3 辽河冲积扇不同α截集与不同保证率下地下水脆弱性指数的隶属度

由表5和图2可知,考虑模糊性参数取不同α截集,得出的脆弱性指数均为区间数,随着α值的增大,脆弱性区间逐渐变小,相应的脆弱性变化范围变小。而α=1时,模糊区间为一点,即不考虑参数的模糊性,仅从随机性方面考虑地下水脆弱性等级。由表5、图2和图3可得以下结论:

a.由图2可知,α越小,模糊性参数所属范围越大,则不确定性越大,脆弱性指数的隶属区间越宽。结合表5和图2,同一α截集下的累积分布曲线取不同保证率,其区间跨度大小基本相同,不同分区模糊性参数通过取同一α截集,脆弱性指数的区间跨度大小可表明各分区参数的变异程度。通过对比分析可得,Ⅰ2和Ⅲ区不确定性程度相对最高,Ⅱ1和Ⅱ2区相对最低,说明Ⅰ2和Ⅲ区水文地质条件更为复杂,结果存在更多可能性,而Ⅱ1和Ⅱ2区参数变化性较小,脆弱性大小在较小区间内变化。

b.由表5和图3可知,地下水脆弱性指数随保证率的增大而增大,同时随α的增大,变化范围逐渐变小。因此地下水环境形势比较严重的地区应该取较大保证率,取得的结果更合理,不确定性程度较大的地区,取较小α截集得到的结果更符合客观实际。分别从不确定性和脆弱性两方面取各研究分区地下水脆弱性的指数隶属区间进行对比分析,Ⅰ1区取α=0.7和95%保证率、Ⅰ2区取 α=0.5和75%的保证率、Ⅰ3区取α=0.5和75%保证率、Ⅰ4区取α=0.7和50%保证率、Ⅱ1区取 α=0.9和50%保证率、Ⅱ2区取α=0.9和50%保证率、Ⅱ3区取α=0.9和75%的保证率、Ⅲ区取α=0.5和95%保证率、Ⅳ区取α=0.7和95%的保证率时最能反映各分区的实际情况。

c.根据以上结论,结合表5分析可得:Ⅰ1区地下水脆弱性程度相对其他区域最高,不确定性程度一般,说明Ⅰ1区大部分地区地下水环境潜在污染性比较高,需限制地下水的大量开采和污染物的排放。Ⅰ2、Ⅰ3、Ⅱ1和Ⅱ3这4个分区为地下水脆弱性程度较高区,这4个分区地处山前坡洪积平原上,含水层岩性主要为砂碎石和砂砾石,地质松散,地下水易遭受污染,其中Ⅰ2和Ⅰ3区不确定性程度相对其他区域更高,局部地区地下水环境存在很大污染风险,需要加强监测,具体情况应具体对待;Ⅱ1和Ⅱ3区不确定性程度相对最低,整体地下水脆弱性较高,需制定整体防治措施。Ⅰ4、Ⅱ2、Ⅲ和Ⅳ区地下水脆弱性程度相对比较低,其中Ⅳ区面积最大,但不确定性程度相对比较低,该分区地势最为低平,地下水补给来源充足,含水层岩性以粉细砂为主,受水流冲击影响最小,沿海地带虽然受海水侵蚀严重,但整体地下水脆弱性程度比较低,不易遭受污染;Ⅲ区面积第二大,该分区被其他冲积扇包围,地势低平,分区内新民以北柳河冲积平原含水层岩性以细砂为主,新民以南以粉细砂为主,不确定性程度较大,大部分地区地下水脆弱性程度不高,但局部地区仍存在较高污染风险,需做好相应的保护工作;Ⅰ4区不确定性程度一般,大部分地区地下水脆弱性程度比较低,但该地区面积比较小,人口密度大,局部地区地下水存在较大污染风险,要做好相应防治措施;Ⅱ2区不确定性程度相对比较低,所以整体地下水脆弱性程度比较低,该区地下水污染风险压力比较小,以防范工作为主。

5 结 论

a.地下水系统中的不确定性对地下水脆弱性的测算会造成一定影响,本文引入蒙特卡罗法和α截集技术,有效处理了参数的随机不确定性和模糊不确定性问题,以累积分布曲线和隶属函数形式表达脆弱性和不确定性符合实际情况,使评价结果更科学合理。

b.参数随机模拟的最终结果依赖于对参数初始值的估计,而利用有限的观测资料给出随机变量的统计特征,使随机模型能准确地刻画出地下水系统自身的随机特性具有一定的难度。因此,参数随机模型仍具有一定的不确定性。

c.Ⅰ1区地下水脆弱性程度相对其他区域最高,不确定性程度相对一般;Ⅰ2、Ⅰ3、Ⅱ1和Ⅱ3区的地下水脆弱性程度较高,且Ⅰ2和Ⅰ3区的不确定性程度相对最高,Ⅱ1和Ⅱ3区的不确定性程度相对其他区域最低;Ⅰ4、Ⅱ2、Ⅲ和Ⅳ区的地下水脆弱性程度相对较低,其中Ⅱ2和Ⅳ区的不确定性程度较低,Ⅰ4区的不确定性程度一般,Ⅲ区的不确定程度较高。

d.本次地下水本质脆弱性评价充分考虑了参数空间分布的随机性与模糊性,但评价过程中其他不确定性问题没有得到解决,如DRASTIC模型中等级划分的模糊性、人类认知的局限性、参数在时间尺度上的变异性以及人为因素的影响,因此考虑时空尺度上的不确定性,综合地下水本质脆弱性与特殊脆弱性的评价具有更深意义。

[1]VRBAJ,ZAPOROZECA.Guidebookonmapping groundwater vulnerability[M]//International Association ofHydrogeologists.InternationalContributionsto Hydrogeology.Hannover:Verlag Heinz Heise,1994: 131.

[2]孙才志,潘俊.地下水脆弱性的概念、评价方法与研究前景[J].水科学进展,1999,10(4):444-449.(SUN Caizhi,PAN Jun.Concept and assessment of groundwater vulnerability and its future prospect[J].Advances in Water Science,1999,10(4):444-449.(in Chinese))

[3]ALMASRI M N.Assessment of intrinsic vulnerability to contaminant on for Gaza coastal aquifer Palestine[J]. Journal of Environmental Management,2008,88(4):577-593.

[4]ANTONAOS A K,LAMBRAKIS N J.Development and testing of three hybrid methods for the assessment of aquifer vulnerability to nitrates,based on the drastic model,an example from NE Korinthia,Greece[J].Journal of Hydrology,2007,333(2):288-304.

[5]NOBRE R C M,FILHO O C R,MANSUR W J,et al. Groundwater vulnerability and risk mapping using GIS, modeling and a fuzzy logic tool[J].Journal of Contaminant Hydrology,2007,94:277-292.

[6]RUPERT M G.Calibration of the DRASTIC ground water vulnerability mapping method[J].Ground Water,2001,39 (4):625-630.

[7]ASSAF H,SAADEH M.Geostatisticalassessment of groundwaternitratecontaminationwithreflectionon DRASTIC vulnerability assessment:the case of the Upper Litani Basin,Lebanon[J].Water Resour Manage,2009, 23:775-796.

[8]JAVADI S,KAVEHKAR N,MOUSAVIZADEH M H,et al.Modification of DRASTIC model to map groundwater vulnerability to pollution using nitrate measurements in agricultural areas[J].Journal of Agricultural Science and Technology,2011,13(2):239-249.

[9]陈守煜,伏广涛,周惠成.含水层脆弱性模糊分析评价模型与方法[J].水利学报,2002(7):23-30.(CHEN Shouyu,FU Guangtao,ZHOU Huicheng.Fuzzy analysis model and methodology for aquifer vulnerability evaluation [J].Journal of Hydraulic Engineering,2002(7):23-30. (in Chinese))

[10]孟宪萌,束龙仓,卢耀如.基于熵权的改进DRASTIC模型在地下水脆弱性评价中的应用[J].水利学报,2007, 38(1):94-99.(MENG Xianmeng,SHU Longcang,LU Yaoru.ModifiedDRASTICmodelforgroundwater vulnerability assessment based on entropy weigh[J]. Journal of Hydraulic Engineering,2007,38(1):94-99. (in Chinese))

[11]孙才志,左海军,栾天新.下辽河平原地下水脆弱性研究[J].吉林大学学报:地球科学版,2007,37(5):943-949.(SUN Caizhi,ZUO Haijun,LUAN Tianxin.Research on groundwater vulnerability assessment of the Lower Liaohe River Plain[J].Journal of Jilin University:Earth Science Edition,2007,37(5):943-949.(in Chinese))

[12]赵春红,梁永平,卢海平,等.娘子关泉域岩溶水脆弱性模糊综合评价[J].水文,2013,33(5):52-57.(ZHAO Chunhong,LIANG Yongping,LU Haiping,et al.Fuzzy evaluation of karst water vulnerability in Niangziguan spring area[J].Journal of China Hydrology,2013,33(5): 52-57.(in Chinese))

[13]张小凌,李峰,刘红战.云南曲靖盆地地下水脆弱性模糊评价[J].水资源与水工程学报,2013,24(4):57-61. (ZHANGXiaoling,LIFeng,LIUHongzhan.Fuzzy evaluation of groundwater vulnerability in Qujing basin [J].Journal of Water Resources&Water Engineering, 2013,24(4):57-61.(in Chinese))

[14]付素蓉,王焰新,蔡鹤生,等.城市地下水污染敏感性分析[J].地球科学:中国地质大学学报,2000,25(5): 482-486.(FU Surong,WANG Yanxin,CAI Hesheng,et al.Vulnerability to contamination of groundwater in urban regions[J].Earth Science:Journal of China University of Geosciences,2000,25(5):482-486.(in Chinese))

[15]孙爱荣,周爱国,梁合诚,等.南昌市地下水易污性评价指标体系探讨[J].人民长江,2007,38(6):10-12. (SUN Airong,ZHOU Aiguo,LIANG Hecheng,et al. Researchofindexsystemusedingroundwater vulnerability in Nanchang[J].Yangtze River,2007,38 (6):10-12.(in Chinese))

[16]刘卓,刘昌明.东北地区水资源利用与生态和环境问题分析[J].自然资源学报,2006,21(5):700-708.(LIU Zhuo,LIU Changming.The analysis about water resource utilization,ecologicalandenvironmentalproblemsin Northeast China[J].Journal of Natural Resources,2006, 21(5):700-708.(in Chinese))

[17]ALLER L,BENNETT T,LEHR J H,et al.DRASTIC:a standardized system for evaluating groundwater potential using hydrogeological settings[R].Ada Oklahoma,US: Robert S.Kerr Environmental Research Laboratory,1985.

[18]黄振平.水文统计学[M].南京:河海大学出版社, 2003.

[19]FREEZE R A.A stochastic-conceptual analysis of onedimensional groundwater flow in nonuniform homogeneous media[J].Water Resources Research,1975,11(5):725-741.

[20]陈彦,吴吉春.含水层渗透系数空间变异性对地下水数值模拟的影响[J].水科学进展,2005,16(4):482-487. (CHEN Yan,WU Jichun.Effect of the spatial variability of hydraulic conductivity in aquifer on the numerical simulation ofgroundwater[J].AdvancesinWater Science,2005,16(4):482-487.(in Chinese))

Assessment of groundwater intrinsic vulnerability in the Lower Reaches of Liaohe River Plain under uncertain conditions//

SUN Caizhi,XI Xu
(College of Urban and Environment,Liaoning Normal University,Dalian 116029,China)

The randomness and fuzziness of hydrogeological parameters in the groundwater system can lead to great error to the evaluation results of groundwater vulnerability.This study is based on the analysis of parameters’uncertainty characteristics by using the Monte Carlo method to assign stochastic and fuzzy parameters at the same time combined with DRASTIC model to evaluate the groundwater intrinsic vulnerability of Lower Reaches of Liaohe River Plain.Through simulation to calculate the different possibilities-cumulative distribution curve of groundwater vulnerability index under different α-cut level of fuzzy parameters,it is possible to deliver the membership interval of groundwater vulnerability index from possibilities-cumulative distribution curves under different reliabilities.Furthermore,the groundwater vulnerability in each partition can be analyzed from vulnerability angle and uncertainty angle.The results show that:areaⅠ1has the highest degree of groundwater vulnerability and average degree of uncertainty;areaⅠ2,Ⅰ3,Ⅱ1andⅡ3has a relatively high degree of groundwater vulnerability,the degree of uncertainty inⅠ2andⅠ3are relatively highest and the degree of uncertainty inⅡ1andⅡ3are relatively lowest;and groundwater vulnerability in areaⅠ4,Ⅱ2,ⅢandⅣare lower,the degree of uncertainty in areaⅡ2andⅣare relatively low and the degree of uncertainty in areaⅠ4is general while the degree of uncertainty in regionⅢis higher.Compared with traditional evaluation process,the groundwater vulnerability assessment based on the analysis of parameters’uncertainty it is possible to calculate the membership function of groundwater vulnerability index under uncertain conditions.The results agree with the objective reality.

groundwater intrinsic vulnerability;hydrogeology;DRASTIC model;uncertainty;Monte Carlo method;α-cut set;cumulative distribution carve;Lower Reaches of Liaohe River Plain

TV211.1+2;P641.8

:A

:1006-7647(2014)05-0001-07

10.3880/j.issn.1006-7647.2014.05.001

20140117 编辑:熊水斌)

教育部博士点基金(20122136110003);国家自然科学基金(40501013)

孙才志(1970—),男,山东烟台人,教授,博士,主要从事水资源与海洋经济研究。E-mail:suncaizhi@lnnu.edu.cn