大型灯泡贯流泵站振动计算方法
李玉莹,高 峰,李清华,杨克坤
(山东省水利勘测设计院,山东济南 250014)
大型灯泡贯流泵站振动计算方法
李玉莹,高 峰,李清华,杨克坤
(山东省水利勘测设计院,山东济南 250014)
为了寻找一种便于设计应用的大型灯泡贯流泵站振动定量分析方法,以南水北调东线工程二级坝泵站为例,对泵站动荷载特性进行了分析,将机组动荷载偏于安全地简化为3个主频谐荷载;根据GB50040—1996《动力机器基础设计规范》并考虑泵站特点,给出了适合泵站振动计算的定量分析方法。将该方法应用于二级坝泵站的振动计算,所得结果为泵站振动的上限值;现场振动检测控制点最大位移值与计算值接近且小于计算值,表明该方法计算结果安全可靠。
灯泡贯流泵站;泵站振动;压力脉动;二级坝泵站;南水北调东线工程
振动是泵站运行中最为常见的问题。机组在运行过程中不可避免地产生振动,当振动超过一定范围,就会影响机组的安全稳定运行,缩短其检修周期和使用寿命,严重时还会引起整个厂房的剧烈振动,以至被迫停机。泵站运行中激振力可能引起的泵房整体或局部振动早已引起人们的重视,但泵站振动问题十分复杂,原因很多,而且多数研究只是局限在理论上的定性分析,针对大型泵站的定量分析较少,尤其对于新型的灯泡贯流泵站。
近年来,随着数值计算水平的提高,研究人员已开始利用动力时程分析方法对泵站振动进行定量分析[1],该方法根据机组生产厂家提供的模型试验中测点的压力脉动时程,利用相似原理,生成机组原型在实际运行时的压力脉动时程作为荷载施加在泵壳上,再利用三维有限元程序对泵站进行振动时程分析[2-6]。动力时程分析方法提高了泵站振动分析水平,但对于多台机组处于同一基础上变频运行的大型灯泡贯流泵站来讲,采用动力时程分析方法进行动力分析存在以下问题[7-9]:①计算量大。采用动力时程分析方法需建立不同频率下的多条动荷载时程曲线进行分析,再加上在运行过程中会出现1台机组单独运行或多台机组联合运行的情况,将会有数十种分析工况,计算量十分巨大。②时程曲线难有代表性。水泵模型试验提供的压力脉动时程曲线除脉动压力幅值和主要荷载频率分量外,不同时段的时程曲线差别较大,以此构造的动荷载时程分析结果难有代表性。③时程分析方法要求较高,难为一般设计人员掌握。因此寻找一种便于设计应用的大型灯泡贯流泵站振动定量分析计算方法十分必要。本文以南水北调东线工程二级坝泵站为例,在分析泵站动荷载特性的基础上,将机组动荷载偏于安全地简化为3个主频谐荷载,根据GB 50040—1996《动力机器基础设计规范》并考虑泵站的特点,推导出适合大型灯泡贯流泵站的振动计算方法。此方法无需借助大型有限元软件,仅采用电子表格就可进行计算,且计算结果为泵站振动的上限值,计算结果简单明了。
1 泵站运行中的动荷载分析
一般认为,引起泵站厂房结构振动的振源有水力、机械和电气三大类。在模型试验中对水力振源可以进行较好的模拟[2],但对于机械和电气振源难以模拟,有些振源也往往难以预见。因泵站机组在制造、施工安装过程中其质量得到了严格控制,机械和电气振源引起的机械不平衡力和电磁不平衡力很小,设计过程中可不予考虑,因此水力振源引起的厂房结构振动是工程人员关注的主要振源。
引起水泵振动的水力振源,一是由于过流部件中流场的速度分布不均匀所产生的压力脉动;二是水流流过某些绕流体(如导叶及叶片)后,脱流的漩涡所诱发出的压力脉动[3]。
对于具体的工程而言,流道内水力脉动压力的研究仍以模型试验为主。以二级坝泵站为例,生产厂家提供了模型泵3个测点的压力脉动时程资料,测点位置如图1所示,测点1位于水泵进口段,测点2位于叶片和导片之间,测点3位于水泵出口段,各测点脉动压力峰值见表1。

图1 压力脉动测点示意图(单位:mm)

表1 各测点脉动压力峰值
二级坝泵站的平均净扬程为1.99 m,设计净扬程为3.21 m,最大净扬程为3.82 m,最小净扬程为0.48 m。压力脉动时程主要的频率分量有ωJ、3ωJ、 24ωJ(ωJ为机组转动角频率)3个,分别称为第一、二、三主频,与机组转动角频率、叶片数(3片)、导叶数(8片)有关。
根据设备厂家提供的资料,水泵原型的脉动压力频率fp与模型的脉动压力频率fm比、原型的工作水头Hp与模型的工作水头Hm比、原型的压力脉动幅值ΔHp与模型的压力脉动幅值ΔHm比均为1,即模型机的脉动压力幅值、脉动压力频率及工作水头均与原型机相同。
脉动压力时程的傅里叶级数展开为
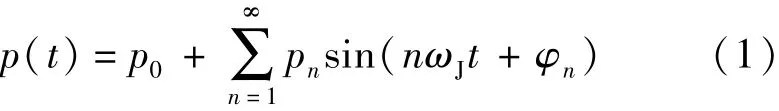
式中:p(t)为脉动压力时间函数;p0为脉动压力的平均值,因动荷载以零值为中心上下震动,故为零; pn为脉动压力第n项幅值;φn为第n项初相位。仅考虑脉动压力时程中3个主要频率对应项对水泵振动的影响,式(1)简化为

由式(2)可知,泵站运行中的脉动压力荷载主要为3项简谐荷载的叠加。设备厂家往往仅能提供p(t)的最大值pmax,不能提供参数p1、φ1、p3、φ3、p24、φ24的具体数值,无法直接利用式(2)进行设计计算。
由前述荷载分析及式(1)可知,相位角φ1、φ3、φ24是随机组合的,p1、p3、p24均不可能大于最大值pmax。为便于分析计算,偏于安全取:

式(2)简化为

这样就把难以处理的泵站动荷载简化为3个谐荷载的叠加。根据GB50040—1996《动力机器基础设计规范》,分别计算在每个谐荷载作用下泵站的振动效应,合成后即为每台泵在动荷载作用下的振动效应。多泵联合运行时,将各台泵的振动效应合成,即为多台泵联合运行的振动效应。
2 泵站的振动计算过程
由于灯泡贯流泵半埋于混凝土中,泵房地下部分由刚度很大的纵横墙及顶板组成,形成刚度很大的箱形结构。泵房的振动简化为实体基础的振动计算问题,见图2(x轴方向为顺水流向,y轴方向为垂直水流向),振动有6个自由度:沿Oz轴的竖向振动,绕Oz轴的扭转振动,沿Ox和Oy轴的水平振动,绕Ox和Oy轴的回转振动。当机组重心O和基础底面形心认为在一条竖直线上时(一般要求偏心距E与偏心方向的基础宽度b的比E/b<0.03),机组振动可分解为相互独立的3种振动:①沿Oz轴的竖向振动;②在xOz及yOz平面内的水平回转耦合振动;③绕Oz轴的扭转振动。这3种振动可分开计算,然后叠加。本文根据GB 50040—1996《动力机器基础设计规范》来推导泵站上述3种振动的计算公式。

图2 泵房计算简图
2.1 竖向振动
机组在受到竖向扰力Pz作用下,其竖向位移计算公式为
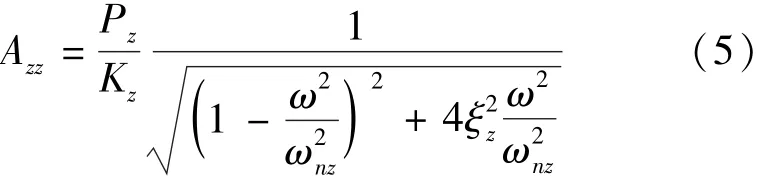
式中:Azz为机组重心处的竖向振动位移,m;Kz为地基抗压刚度,kN/m;ω为机组的扰力圆频率,rad/s; ωnz为机组的竖向固有频率,rad/s;ξz为地基竖向阻尼比;m为机组的质量,t。
2.2 水平回转耦合振动
机组在水平扰力Py和竖向扰力Pz沿y轴向偏心距作用下,产生y轴向水平、绕x轴回转的耦合振动(图3),其基础顶面控制点M的竖向和水平向振动位移计算公式为

图3 机组沿y轴向水平、绕x轴回转的耦合振动振型
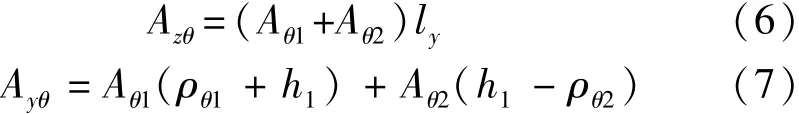
其中

式中:Azθ、Ayθ分别为基础顶面控制点M由于y轴向水平、绕x轴回转耦合振动产生的竖向振动位移和y轴向水平振动位移,m;Aθ1、Aθ2分别为机组y-θ向耦合振动第一、二振型的回转角位移,rad;ρθ1、ρθ2分别为机组y-θ向耦合振动第一、二振型转动中心至机组重心的距离,m;ωnθ1、ωnθ2分别为机组y-θ向耦合振动第一、二振型的固有圆频率,rad/s;ωny为机组y轴向水平固有圆频率,rad/s;ωnθ为机组绕x轴回转固有圆频率,rad/s;ξyθ1、ξyθ2分别为y-θ向耦合振动第一、二振型阻尼比;Jx为机组对通过其重心的x轴的转动惯量,t·m2;Mθ1、Mθ2分别为绕通过y-θ向耦合振动第一、二振型转动中心Oθ1、Oθ2并垂直于回转面zOy的轴的总扰力矩,kN·m;Kx为地基抗剪刚度,kN/m;Kθ为机组绕x轴的抗弯刚度,kN·m;Cφ为地基刚度系数,kN/m3;Ix为机组对通过底面形心x轴的惯性矩,m4;ey为机组竖向扰力沿y轴的偏心距,m。
2.3 扭转振动
机组在受到扭转扰力矩Mφ和水平扰力Px沿y轴向偏心作用下,其水平扭转位移计算公式为
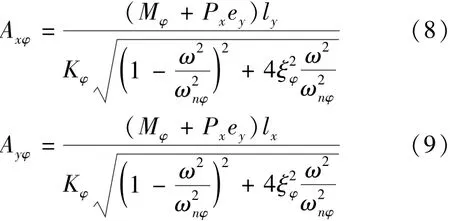
式中:Axφ、Ayφ分别为基础顶面控制点M由于扭转振动产生的沿x、y轴向的水平振动位移,m;ly为基础顶面控制点M至扭转轴在y轴向的水平距离,m;lx为基础顶面控制点M至扭转轴在x轴向的水平距离,m;Jz机为组对通过其重心轴的极转动惯量, t·m2;ωnφ为机组扭转振动固有圆频率,rad/s;Kφ为机组绕z轴的抗扭刚度,kN·m。
2.4 单台泵引起的控制点位移计算
在振动计算时,选取振动位移峰值最大的点作为控制点进行计算。单台泵振动引起的控制点沿机组坐标x、y、z轴方向的振动位移峰值Ax、Ay、Az计算公式为

式中:A′、A″、A‴分别为第一、二、三主频扰力和扰力矩产生的振动位移幅值,m。
2.5 多台泵引起的控制点位移计算
多台泵同时运行引起的联合振动,分别计算各台泵在第一、二、三主频扰力和扰力矩作用下产生的各向振动位移幅值。总振动位移取各台泵扰力和扰力矩作用下的振动位移平方之和的开方值。
多台泵振动引起的控制点沿机组坐标x、y、z轴方向的振动位移峰值Ax、Ay、Az计算公式为

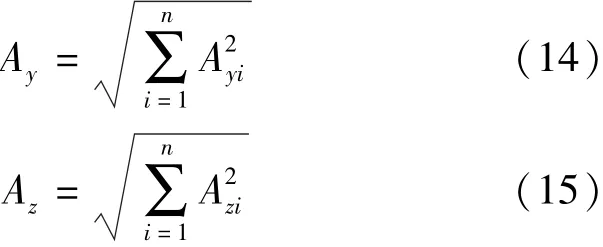
式中:Axi、Ayi、Azi分别为第i台泵产生的沿机组坐标x、y、z轴方向的振动位移幅值,m。
3 二级坝泵站振动计算

图4 泵站纵剖视图(单位:高程m,尺寸mm)
二级坝泵站是南水北调东线工程的第十级抽水梯级泵站,位于南四湖中部,山东省微山县欢城镇二级坝以南的下级湖内。工程规模为大(Ⅰ)型工程,泵站等别为Ⅰ等。下面给出主要计算成果。
泵站主厂房内安装5台3000HSTM型后置式灯泡贯流泵,其中备用1台。水泵叶轮直径3000 mm,灯泡体直径3120mm,机组额定转速115.4r/min。泵站安装5台高压变频调速器,水泵最高效率工况点在平均净扬程1.99 m附近,泵站运行时间较长的扬程区域(H=1.50~2.7m)采用额定转速运行,无变频器能耗,机组总效率最高;泵站运行时间较短的高扬程区域(H=2.7~3.82 m)采用升速运行,升速范围115~127r/min;出现频率较低的低扬程区域(H=0.48~1.50m)采用降速运行,降速范围86~115r/min。
泵站厂房地下埋深18.5 m,采用块基型基础(图4),自上而下共4层(厂区地面高程为38.00 m):地上1层(厂房层),地下3层,其中地下一层上游侧布置励磁柜、LCU、检测设备等,下游侧布置变频器、旁路柜、电抗器等电器设备;地下二层上游侧布置供水站,下游侧布置电缆室等;地下三层由进水流道、泵组段、出水流道组成。水泵外壳半埋于混凝土中,与厂房形成整体。厂房顺水流方向长41.80 m,垂直水流方向长55.98 m。基本动参数按规范GB 50040—1996《动力机器基础设计规范》第3.3.2~3.3.11条规定确定。根据泵站各构件的尺寸、质量参数,计算机组的重心位置及振动参数。
单泵运行分为5种工况,如表2所示。泵站可单泵或多泵联合运行,经分析,离机组重心距离越大的泵产生的振动越大,为简化计算,取表3组合进行计算。

表2 机组运行工况及对应主要频率rad/s

表3 泵的运行组合
图1仅有3个测点,测点数据很难精确反映泵站整个流道的压力脉动场。参照抽水蓄能电站内压力脉动的分布规律[5-6],立足于3个测点数据,假设进出水口处的压力脉动值为零,对进出水口和3个测点共5个位置之间的其他流道位置压力脉动作线性插值处理,如图5所示。
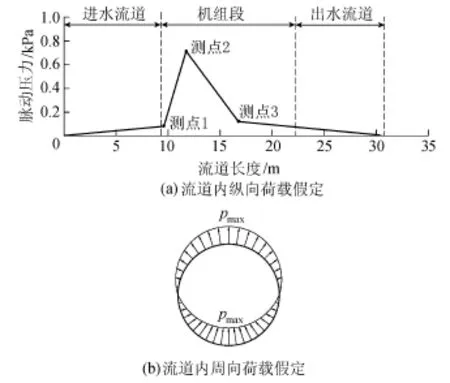
图5 流道内脉动压力假定
以泵房边墙处振幅最大点为控制点进行振动计算,计算结果见表4和表5。
由表4和表5可见,采用本文方法可以方便地计算泵站单泵和多泵联合运行的振动位移,解决了设计中的计算难题。二级坝泵站的振动计算结果满足GB50265—2010《泵站设计规范》要求机组最大垂直振幅不超过0.15 mm、最大水平振幅不超过0.20 mm的要求。
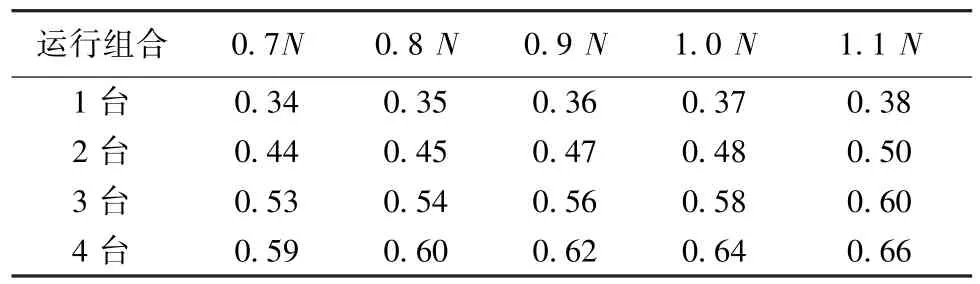
表4 控制点z向振动位移计算结果 μm
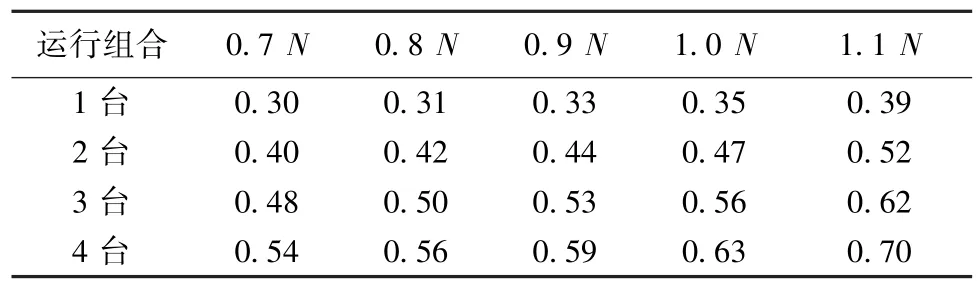
表5 控制点y向振动位移计算结果 μm
4 现场振动检测
2012年6月18—19日,二级坝泵站进行了各种组合的机组联合试运行,试运行时扬程为2.24m,单泵流量30.48 m3/s。在高程29.77 m的楼面布置传感器对主厂房在不同工况下的加速度时程进行检测(委托山东大学进行)。通过对部分不同泵的开机和关机实测分析,各测点中最大位移0.1 μm,均小于计算结果,表明本文计算方法所得计算结果是上限解,计算方法安全可靠。
5 结 语
根据灯泡式贯流泵动力荷载特点,将动荷载简化为3个谐荷载进行振动计算的方法简便可行。由二级坝泵站计算结果可知,采用本文方法计算,计算结果大于实测值,验证了该方法为泵站振动计算的一个上限解方法,是一种简便可行的定量计算方法,计算结果安全可靠,可为相同的工程设计提供计算依据。
[1]马震岳,董毓新.水电站机组及厂房振动的研究与治理[M].北京:中国水利水电出版社,2004.
[2]唐昶,程云山.广西麻石水电站2号机组振动原因分析及处理[J].水利水电科技进展,2004,24(增刊1):67-68.(TANG Chang,CHENG Yunshan.Causes of vibration of No.2 hydrogenerator unit at Mashi hydropower plant of Guangxi and measures for its treatment[J].Advances in Science and Technology of Water Resources,2004,24 (Sup1):67-78.(in Chinese))
[3]王玲花.水轮发电机组振动及分析[M].郑州:黄河水利出版社,2011.
[4]董毓新.水轮发电机组振动[M].大连:大连理工大学出版社,1989.
[5]欧阳金惠,陈厚群,李德玉.三峡电站厂房结构振动计算与试验研究[J].水力学报,2005,36(4):1-9.(OUYANG Jinhui,CHEN Houqun,LI Deyu.Computation of vibration in powerhouse of Three Gorges Project and prototype verification[J].Journal of Hydraulic Engineering,2005,36 (4):1-9.(in Chinese))
[6]王新,李同春,潘树军.淮阴三站泵站振动分析[J].水利水电科技进展,2008,28(5):49-53.(WANG Xin,LI Tongchun,PAN Shujun.Vibration analysis of the pumphouse of the third Huaiyin Pumping Station[J].Advances in Science and Technology of Water Resources,2008,28 (5):49-53.(in Chinese))
[7]杨位洸.地基及基础[M].北京:中国建筑工业出版社, 1998.
[8]CARIDAD J,KENYERY F.CFD analysis ofelectric submer-sible pumps(EPS)handing two-phase mixtures[J]. Transaction of the ASM E:Journal of Energy Resource Technology,2004,126(2):99-102.
[9]LI Yaojun,WANG Fujun.Numerical investigation of performance of an axial-flow pump with inducer[J].Journal of Hydrodynamics,2007,19(6):705-711.
Computing method of vibration in large bulb tubular pump system//
LI Yuying,GAO Feng,LI Qinghua,YANG Kekun
(Water Conservancy and Hydropower Survey and Design Institute,Jinan 250014,China)
In this work,we propose a quantitative analysis method of vibration for large bulb tubular pump station,which is easy to design and apply,by taking Erjiba Pumping Station in East Route of South-to-North Water Transfer Project as an example.Furthermore,we analyze the dynamic load properties of the pump station and then find that the dynamic load of machine set can simplify into three main frequency harmonic loads with a little safety.Referring to GB 50040-1996 The Primary Design Principles on Dynamic Machine and the characteristics of pump station,we provide a suitable quantitative analysis method for calculating the vibration of a pumping station.The paper applied this method to calculate the vibration of Erjiba Pumping Station and the result clearly presents the upper limit.The control point of maximum displacement, tested by vibration detection,is slightly less than calculated values indicating that the quantitative analysis method is safe and reliable.
bulb tubular pump system;pumping vibration;pressure pulsation;Erjiba Pumping Station;East Route of South-to-North Water Transfer Project
TV75
:A
:1006-7647(2014)05-0069-06
10.3880/j.issn.1006-7647.2014.05.014
2013-0722 编辑:熊水斌)
李玉莹(1970—),男,山东东营人,高级工程师,博士,主要从事水工结构设计与研究。E-mail:lyy7705@163.com

