输电线路绕击耐雷性能对比研究
杨威,税少洪
(1.江西省电力公司检修分公司,江西南昌330043;2.南京南瑞继保电气有限公司,江苏南京211000)
输电线路绕击耐雷性能对比研究
杨威1,税少洪2
(1.江西省电力公司检修分公司,江西南昌330043;2.南京南瑞继保电气有限公司,江苏南京211000)
指出雷电绕击引起的输电线路跳闸事故随电压等级的升高所占的比例越来越大。针对220 kV、500 kV电压等级典型线路,分别利用规程法、优化法和电气几何模型法分析绕击耐雷性能,并对其结果进行分析比较。结果表明,优化法与规程法相比,电压等级越高,两者所得绕击跳闸率的差别越大;地面倾角是影响线路绕击跳闸率的重要因素之一,将地形简单地分为平原和山区不切合实际;对平原地区线路来说,用三种方法所得绕击跳闸率差别不大,可以用规程法和优化法对平原地区线路绕击耐雷性能进行简单估算;电气几何模型则更好地解释了山区线路绕击跳闸率异常高的现象。
输电线路;绕击跳闸率;规程法;优化法;电气几何模型法
架空输电线路是电力系统的大动脉,地处旷野,纵横延伸,极易遭受雷击。研究表明,雷击是输电线路安全可靠运行的主要危害[1-3],随着电压等级的提高,雷电绕击导线已经成为主要的雷害形式[4、5]。因此,准确计算和评价线路的绕击耐雷性能对保证系统安全稳定运行尤为重要。
近年来,国内外学者提出了多种研究输电线路绕击耐雷性能的方法和模型。由于雷电放电过程的数据难以准确测量;绕击物理过程不够清晰,难于对其精确模拟,致使在对输电线路绕击耐雷性能进行分析时,建立在一定的假设基础上,使得不同方法的计算结果出现较大偏差。因此,进一步研究输电线路的绕击耐雷性能非常重要。
本文选用220 kV和500 kV典型线路,分别用规程法、优化法和电气几何模型法对绕击耐雷性能进行计算,并对其结果进行比较,分析各种方法的优点和不足。
1 规程法
我国现行标准中,绕击耐雷水平的计算忽略了避雷线和导线的耦合作用以及杆塔接地的影响。雷电绕击线路的耐雷水平为

式中,u50%为绝缘子串的50%冲击闪络电压;Z为输电线路的波阻抗,取400Ω。
我国DL/T620—1997标准推荐的雷电流幅值的概率分布为

对于雷电活动很弱的少雷地区(年平均雷电活动20日以下),雷电流幅值概率密度的计算公式为

式中,I为雷电流幅值,kA;P为幅值大于I的雷电流概率。
设N为100 km/a线路(40个雷电日)遭受雷击的次数,则N可由公式(4)计算。

式中,γ为地面落雷密度,按我国标准取值γ=0.07;b为两避雷线直接的距离,m;hb为避雷线平均高度,m。
根据模拟试验、现场实测以及运行经验,绕击率Pα与避雷线对外侧导线的保护角、杆塔高度以及沿线的地形、地貌以及地质条件有关,可近似按照公式(5)、(6)计算。

式中:α——避雷线对外侧导线的保护角,(°);
hb——避雷线的平均高度,m。
线路冲击闪络中,可能转为稳定工频电弧的比例,称为建弧率。根据实验室的实验数据和线路运行经验的分析结果,建弧率可按公式(7)计算。

式中:E——绝缘子串的平均运行电压梯度,kV/m。
设n为线路绕击跳闸率,基于规程法的线路绕击跳闸率的计算公式为

规程法是根据现场经验和小电流实验总结得出的近似计算方法,能够满足一般线路的防雷屏蔽设计要求,但不能反映线路的特点,也不能解释屏蔽失效现象。
2 优化法
优化法又称改进规程法,是在规程法的基础上,考虑线路避雷线和导线的耦合作用对导线绕击耐雷性能造成的影响,此影响集中反映在导线的等值波阻抗上。
2.1 单根避雷线线路绕击时等值波阻抗的计算
如图1所示单避雷线线路,导线遭受绕击时,可得行波方程。

将边界条件u1=0代入式(9)可得导线2的等值波阻抗,得到

相比于忽略避雷线影响的导线波阻抗,计及避雷线耦合作用影响使得导线等值波阻抗有所降低。
引入波阻抗变化值ΔZ,定义波阻抗变化值为

式中,Zd为导线自阻抗,Ω;ZE为考虑避雷线影响时导线的等值阻抗,Ω。
根据定义可知,波阻抗变化值ΔZ集中反映了避雷线对导线等值波阻抗的影响。波阻抗变化值ΔZ越大,说明避雷线对导线等值波阻抗的影响越大;反之,波阻抗变化值ΔZ越小,说明避雷线对导线等值波阻抗的影响越小。
则对于单避雷线线路,波阻抗的变化值为

2.2 双避雷线线路绕击时等值波阻抗的计算
如图2所示双避雷线线路,导线遭受绕击时,可得行波方程。
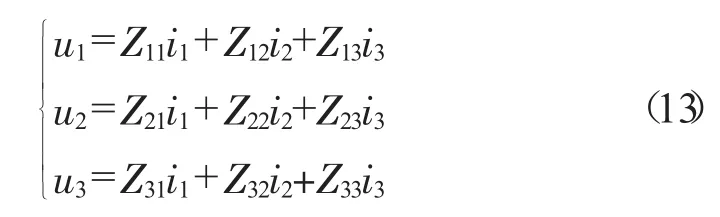
将边界条件u1=0,u2=0代入公式(13)可得导线3的等值波阻抗。

对于双避雷线线路,导线3波阻抗的变化值为

在运用优化法进行计算时,采用导线的等值波阻抗。根据公式(10)及公式(14)可以判断,计及避雷线影响后,导线的等值波阻抗与自波阻抗相比有所降低,可以预知,与不考虑避雷线影响情况相比绕击耐雷水平将会有所提高,绕击跳闸率将会有所降低。
3 电气几何模型法
3.1 经典电气几何模型法
经典电气几何模型是指将雷电的放电特性与线路的结构尺寸联系起来而建立的一种几何分析计算模型[6,7],计算模型如图1所示。

图1 经典电气几何模型
对不同幅值的雷电流,可由击距公式求得相应的击距[8]。当先导进入屏蔽弧面AiBi时,雷电将击向避雷线;当先导进入暴露弧面AiBi时,雷电将绕击导线;当雷电离杆塔稍远时,先导离地面最近,雷电将直接击于地面物体。随着雷电流幅值的增大,击距将随之增大,暴露弧AiBi会逐渐缩小。当雷电流幅值增大到Im时,AiBi弧段缩减到零,此时不可能发生绕击。对应于Im的击距称为临界击距rsm。
经典电气几何模型假设雷电先导对导线、对避雷线及对大地三者的击距相等,并提出了击距的概念。将雷电的放电特性与线路的结构尺寸联系起来,成功地解释了输电线路遭受绕击的原因。但该模型也存在诸如未考虑线路高度等其他因素对击距的影响等不足之处。
3.2 改进电气几何模型法
在经典电气几何模型法之后出现了多种改进电气几何模型[9-13]。Eriksson考虑了结构物高度对输电线路雷电绕击的影响,提出了改进电气几何模型,如图2所示,其中弧段AiBi为屏蔽弧,弧段BiCi为暴露弧。分析方法和经典电气几何模型一致,随着击距rsi的变化,暴露弧段的大小也将发生变化。如果在某一个rsi值情况下,弧段BiCi减小到0,则线路将不再会受更大雷电流绕击,此时击距即为最大击距rsm。
依据图2的改进电气几何模型,将暴露弧与屏蔽弧组成的整段弧称之为弧段,若暴露弧在弧段中所占的比例大,那么导线被雷击中的概率相应的就大,屏蔽失效也更容易发生。反之,雷电将更容易击中避雷线。

图2 Eriksson改进的电气几何模型
在改进电气几何模型中,受雷宽度是指输电线路上空的一个狭长空间,主要取决于雷电流幅值,线路的等效受雷宽度可由公式(16)求得。

式中:bc——两根边相导线间距离,m;
rs——击距,m。
电气几何模型的核心是击距与雷电流幅值的函数关系,击距与雷电流幅值的关系可表示为rs=a Ib。不同的学者,给出了不同的a、b值。

不考虑先导入射角的分布,假定所有先导全部垂直向下,先导头部处于对相导线闪络的空间位置的条件概率x为

式中:L1——电气几何模型的暴露弧长度,m;
L2——电气几何模型的屏蔽弧长度,m。
绕击率为

线路绕击跳闸率为

式中:Ns——线路的落雷次数,100 km·a/次;
Ng——地面落雷密度,km2·a/次;
B——引雷宽度,m。
改进电气几何模型法同经典电气几何模型法相比更接近于实际。但是该方法也存在一些不完善之处,如吸引距离同结构物高度的关系是否准确等。
4 实例分析比较
4.1 典型输电线路的选取
输电线路各导、地线之间的位置主要由杆塔确定,所以要选取典型杆塔进行分析计算。220 kV线路杆塔基本参数:导线型号LGJ-400,地线型号GJ-70,水平挡距600m,垂直挡距800m,绝缘子片数13片,绝缘子串长2.2m,线路绝缘子冲击闪络电压u50%=1 199 kV。500 kV线路杆塔基本参数:导线型号4×LGJQ-300,地线型号LBGJ-120,水平挡距600m,垂直挡距850 m,绝缘子片数28片,绝缘子串长4.7m,线路绝缘子冲击闪络电压u50%=2 466 kV。
4.2 规程法及优化法计算分析
运用规程法和优化法对线路绕击耐雷水平和绕击跳闸率进行计算,结果如表1所示。

表1 规程法和优化法计算绕击耐雷性能计算结果
由表1可以看出,当考虑线路避雷线的耦合作用,即运用优化法进行线路绕击耐雷性能计算时,与规程法计算相比,两种电压等级的导线等值波阻抗计算所得值与规程规定的计算所用400Ω相比均有所下降,导致运用优化法计算所得两种电压等级的耐雷水平与规程法相比有所升高,绕击跳闸率有所降低。对于220 kV线路来说,优化法所得耐雷水平值与规程法相比增大了26.36%;平原和山区绕击跳闸率分别降低了8.43%和8.08%。对于500 kV线路来说,优化法所得耐雷水平值与规程法相比增大了26.93%,与220 kV线路相比差别不大;平原和山区绕击跳闸率分别降低了17.82%和17.96%,为220 kV线路降低百分比的2倍。
可以看出,220 kV线路运用优化法所得绕击跳闸率与规程法相比虽有一定的差距,但是误差在10%以内,避雷线耦合作用影响不大。但是随着电压等级的升高,对500 kV线路分别运用规程法和优化法计算时,所得绕击跳闸率误差增大到将近20%。因此,在对输电线路,特别是电压等级较高的输电线路进行绕击耐雷性能分析计算时,建议考虑雷绕击导线时避雷线与导线之间的耦合作用。
4.2 电气几何模型法计算分析
山区地形复杂,线路杆塔处于不同地面倾角的山坡上,导致绕击情况复杂。我国的规程法仅用平原和山区来区分地形,不能有效定量地评估地形对线路绕击跳闸率的影响。在电气几何模型中,地形与地貌通过地面倾角来描述,并将雷电放电特性与线路结构尺寸联系起来,能够反映具体线路的特点。
本节根据电气几何模型法(EGM)的基本原理,利用MATLAB编程计算线路的绕击跳闸率,并将所得结果与规程法以及优化法所得雷击跳闸率进行对比。仿真分析所选220 kV输电线路和500 kV输电线路绕击跳闸率计算条件如表2所示。
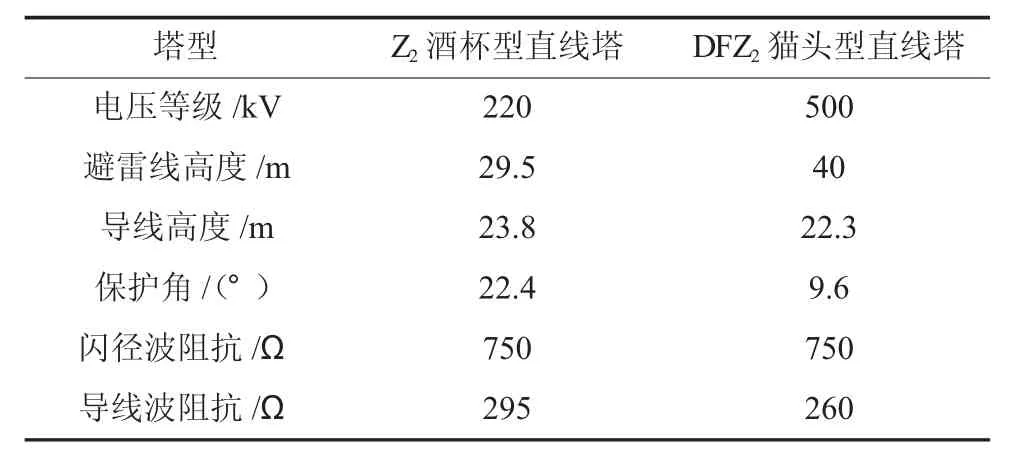
表2 输电线路绕击跳闸率计算条件
根据以上计算条件,仿真所得不同地面倾角下所选杆塔线路的绕击跳闸率如表3所示。

表3 不同地面倾角下输电线路绕击跳闸率计算结果
运用电气几何模型原理编程仿真地面倾角对输电线路绕击跳闸率的影响可以看出,地面倾角对输电线路绕击跳闸率的影响较大,且绕击跳闸率随地面倾角的增大而增大。以220 kV Z2酒杯型直线塔为例,当地面倾角为0°(可认为是平原地区)时,电气几何模型法仿真所得线路绕击跳闸率与规程法和优化法相比差别不大;当地面倾角为5°时,仿真所得绕击跳闸率为每100 km 0.2774次/a;当地面倾角增大到25°时,仿真所得绕击跳闸率为每100 km 2.645 7次/a,地面倾角增大了5倍,而仿真所得绕击跳闸率增大了9.54倍。而由规程法和优化法计算公式可以看出,不论是平原地区还是山区地区,规程法和优化法输电线路绕击跳闸率的大小几乎是只决定于杆塔的保护角,保护角大的杆塔线路的绕击跳闸率就高,反之则低,忽略了地面倾角对绕击跳闸率的影响,这与实际情况是不相符的。通过经典电气几何模型法可知,在对输电线路绕击耐雷性能进行分析时,不能简单地将地形分为山区和平原进行计算。
由此可知,运用电气几何模型分析输电线路绕击跳闸率时,比规程法和优化法更接近实际,而且通过电气几何模型法分析不同地面倾角对输电线路绕击跳闸率的影响,可以很好地解释山区线路绕击跳闸率异常高现象的同时,还可作为山区线路绕击跳闸率的一种定量计算方法来进行山区线路绕击跳闸率的估算。
5 结论
本文针对不同电压等级、不同杆塔线路,分别利用规程法、优化法计算得到绕击耐雷水平及绕击跳闸率,根据电气几何模型方法,通过MATLAB编程计算得到了其绕击跳闸率,最后对三种方法的计算结果进行对比与讨论,得出主要结论如下。
a)优化法与规程法相比考虑了导线自波阻抗以及避雷线与导线耦合作用的影响,导致线路电压等级越高,两者所得线路绕跳闸率相差越大。
b)计算线路绕击跳闸率时,不能简单地将地形分为平原和山区,地面倾角是影响线路绕击跳闸率的重要因素之一。
c)对平原地区输电线路来说,用三种方法所得绕击跳闸率相差不大,可以用规程法和优化法对平原地区线路绕击跳闸率进行估算。
d)电气几何模型法很好地解释了山区线路绕击跳闸率异常高的现象,可作为一种定量计算对山区线路绕击跳闸率进行分析。
[1]钱冠军,王晓瑜,丁一正,等.500 kV线路直击雷典型事故调查研究[J].高电压技术,1997,23(2):72-83.
[2]李培国.国外对特高压输电线路雷击跳闸原因的一个新观点[J].电网技术,2000,24(7):63-65.
[3]陈国庆,张志劲,张才新,等.输电线路耐雷性能计算方法的研究现状分析[J].重庆大学学报,2003,26(5):137-142.
[4]谷定燮,樊灵孟.对我国500 kV线路防雷的新思考[J].中国电力,2004,37(12):18-21
[5]铁冠军.500 kV线路直击雷典型事故调查研究[J].高电压技术,1997,23(2):73-75.
[6]Brown G W,Whitehead E R.Field and analytical studies of transmission line shielding(partⅡ)[J].IEEE Trans on Power Apparatusand System,1969,88(5):617-626.
[7]王晓彤,施围,刘文泉.改进电气几何模型计算输电线路绕击率[J].高电压技术,1998,24(1):85-87.
[8]赵斌财,周皓,钟一俊,等.输电线路雷电绕击研究方法浅议[J].电磁避雷器,2008,1(221):29-34.
[9]ERIKSSON A J.An Improved Electroge metric Model for Transmission Line Shielding Analysis[J].IEEE TPWRD,1987,2(3):859-970.
[10]RIZK F A M.Modeling of Transmission Line Exposure to Direct Lighting Strokes[J].IEEETPWRD,1990,5(4):1983-1997.
[11]张志劲,司马文霞,蒋兴良,等.高杆塔下击距系数的研究[J].高电压技术,2005,31(4):16-18.
[12]李晓岚,尹小根,余仁山,等.基于改进电气几何模型的绕击跳闸率的计算[J].高电压技术,2006,32(3):42-44.
[13]蓝磊,邓维,黄文武,等.平原地区500 kV输电线路雷电屏蔽性能的模型试验研究[J].电网技术,2006,30(9):72-76.
Com parative Study on Lightning Shielding Failure Proof Performance of Transm ission Lines
YANG Wei1,SHUIShao-hong2
(1.State Grid Jiangxi Electric Power M aintenance Company,Nanchang,Jiangxi 330043,China;2.Nanjing Nari Relays Electric Co.,Ltd.,Nanjing,Jiangsu 211000,China)
With the increase of voltage levelof transmission lines,the proportion ofoutages because of shielding failure increases. The shielding performance of220 kV and 500 kV typical transmission linesare analysed by using standardmethod,optimizationmethod and electric-geometrymodel,and the resultsare calculated and compared.The results show that the higher the voltage level is,the larger the difference of lighting trip-out rates is.The ground angle is one of the important factors thataffect lighting trip-out rates,thus,it is not realistic to simply divide the terrain type into plains and themountains.There is notmuch difference of lighting trip-out rates by using the three methods in the plain region,and the standard method and optimization method can be used to simply estimate the shielding performance atplain regionwhile electric-geometrymodel can better explain the phenomenon ofabnormally high lighting trip-out rates in mountain region.
transmission line;lightning shielding failure trip-out rate;standardmethod;optimizationmethod;electric-geometry model
TM862
A
1671-0320(2014)05-0046-05
2014-06-30,
2014-08-12
杨威(1967-),男,浙江杭州人,1991年毕业于江西电力职工大学继电保护专业,工程师,高级技师,从事继电保护技术管理及电力系统故障分析;
税少洪(1983-),男,四川自贡人,2006年毕业于重庆大学电气工程学院电力系统专业,工程师,从事继电保护设备的设计。

