非线性边界流下薄膜方程解的存在性

王美珊，梁波，沈慧颖

(大连交通大学 理学院，辽宁 大连 116028)*

0 引言

薄膜类型的方程可用来描述很多实际的自然现象或物理过程，如热力学中的扩散现象、生物种群的竞争与排斥、流体流过物体表面的扩散过程等.薄膜方程的研究开始于F.Bernis，A.Friedman(JDE，1990)［1］，他们给出了问题

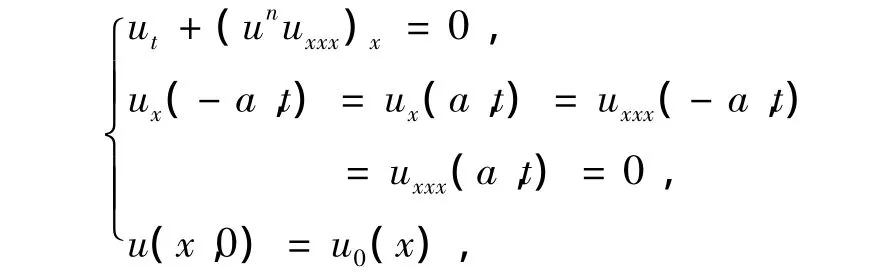
一类Hölder连续弱解的存在性，并讨论了初值及参数在一定范围内解的非负性，主要采用正则化办法及Höllder模的估计.其中函数u表示薄膜的高度或厚度，常数n＞0.由于最大值原理及比较原理不成立，所以四阶偏微分方程的研究主要是利用能量估计的方法，有关文献还可参考［2－5］.

本文主要考虑下面的初边值问题:

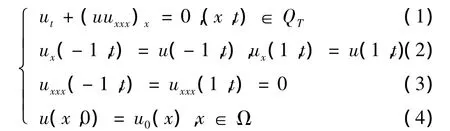
其中，u0∈H1(Ω)，u0≥0，Ω =(－ 1，1)，QT= Ω ×(0，T)时解的存在性和正性.

主要结论为下述定理:

定理1 称问题(1)～(4)存在弱解，满足:

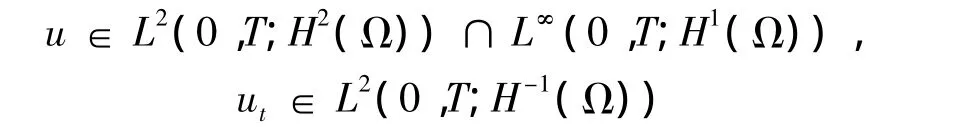
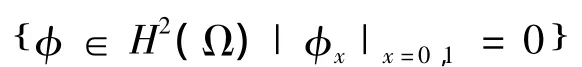
1 逼近问题

首先考虑问题(1)～(4)的正则化逼近方程:

其中，δ＞ 0，u+=max{0，u}.

引理1 称问题(5)～(8)存在弱解，若其满足

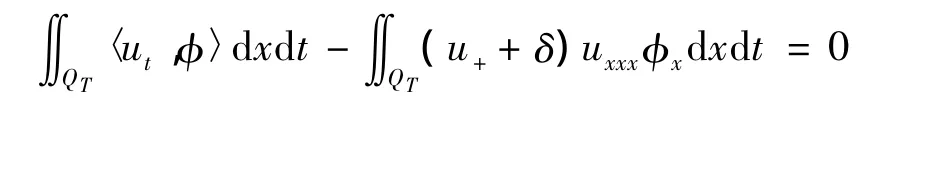
证明 在方程(5)两端同时乘以函数uxx，然后在QT上做积分，可得:

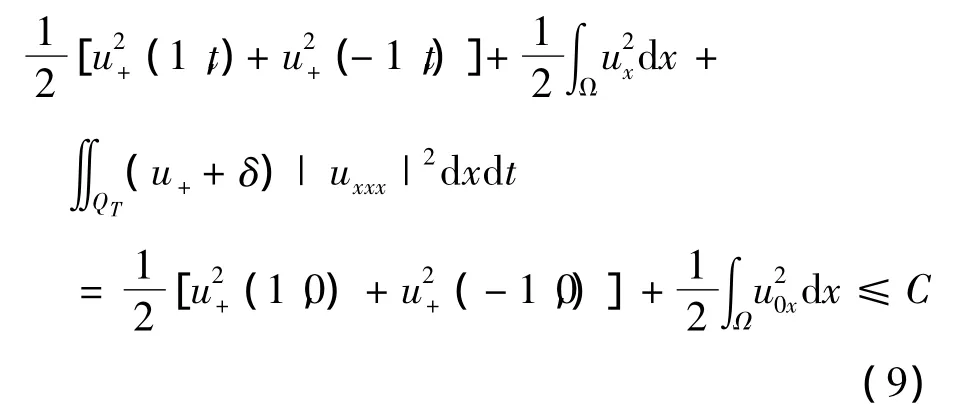
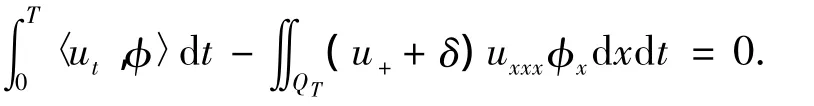
利用Hölder不等式，可得到:

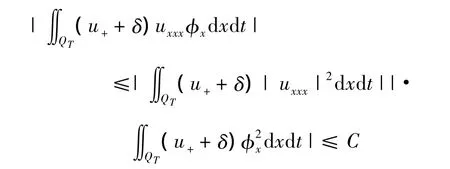
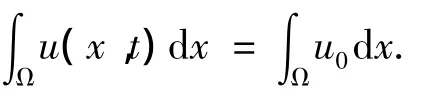
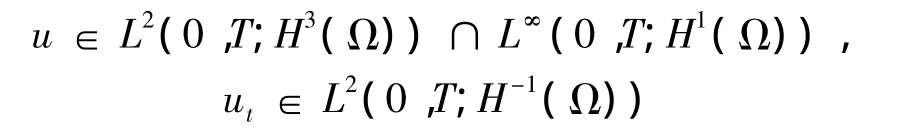
2 存在性

接下来主要是证明逼近解uδ所满足的一些估计，而且uδ不依赖于δ.首先建立如下函数［3］:

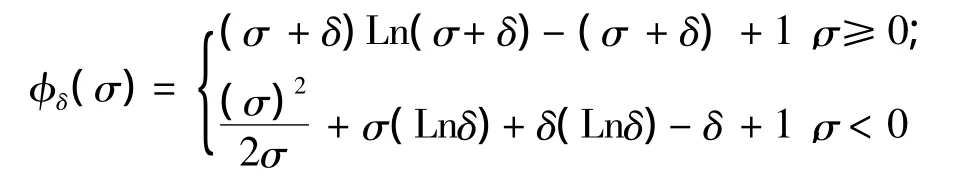
其中，φδ≥0，φδ∈(R)，则有 φ″δ(σ)=

引理 2 (Gagliardo － Nirerberg 不等式)［4］令u∈H1(Ω)，则满足下面的不等式:

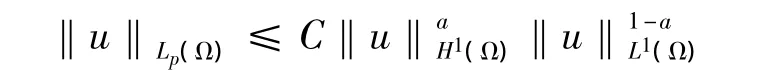
引理3 称问题(5)～(8)存在弱解uδ，则下式成立:

其中，C是不依赖于δ的常数.

证明 在方程(5)两端同时乘以函数φ″δ(uδ)，然后在 QT上做积分，可得:

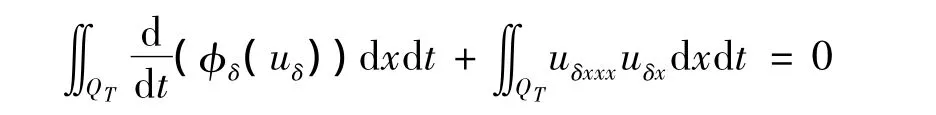
由于ux(－1，t)=u+(－1，t)，ux(1，t)= －u+(1，t)，因此对于上式不可直接利用分部积分来计算，我们需要构造新的辅助函数(－x)uδ+，则有

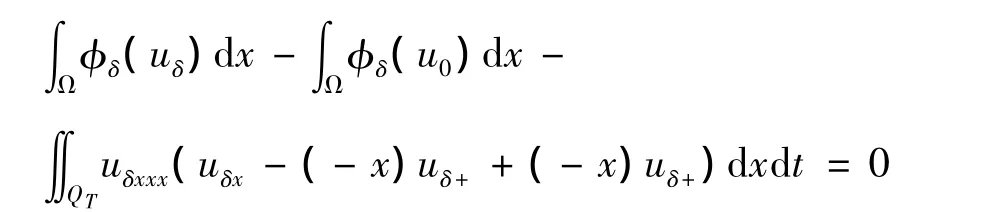
此时，uδx－(－x)uδ+满足零边界，通过分部积分得到:

通过利用Gagliardo－Nirerberg不等式并结合等式(9)，此引理得证.

引理4 假设问题(5)～(8)存在弱解u，当δ→0时，满足:

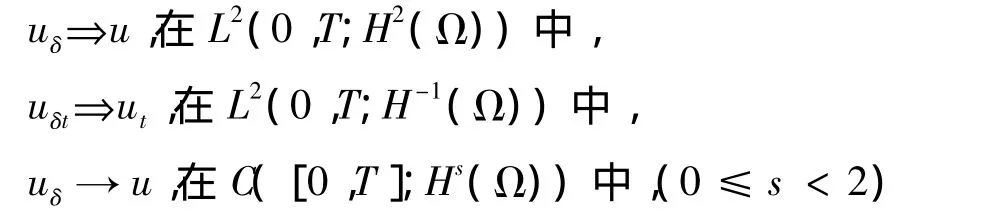
则有u≥0.在这里“⇒”表示弱收敛.

证明 由引理2和引理3，可得到如下估计:

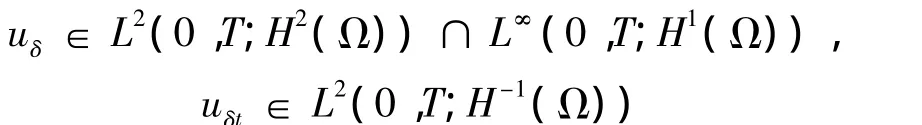
通过利用弱列紧性和紧嵌入定理［4］，当δ→0时，得到:

uδ⇒u，在 L2(0，T;H2(Ω))中，

uδt⇒ut，在 L2(0，T;H－1(Ω))中，

uδ→ u，在 C(［0，T］;Hs(Ω))中，(0≤ s ＜ 2)

和 u∈ L2(0，T;H2(Ω))∩ C(［0，T］;Hs(Ω))，

从而有

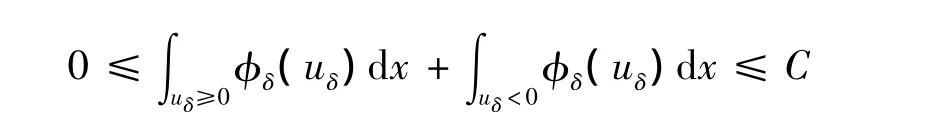
由φδ的定义，可得出:

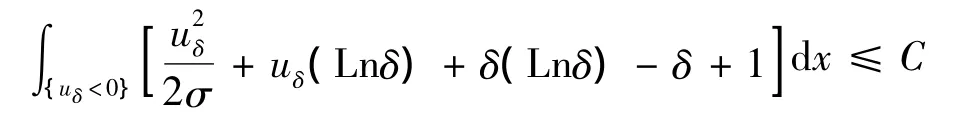
此外，当0 ＜ δ＜ 1时，δ(Lnδ)－ δ+1≥0，有

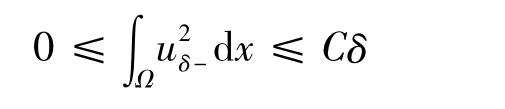
最后，来完成对定理1的证明.

证明 由引理2，对于检验函数φ∈L2(0，T;H*(Ω))，可得到:

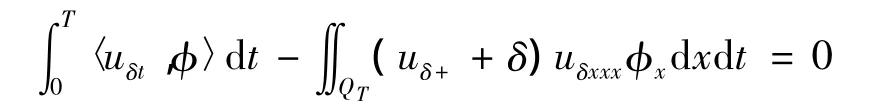
对上式进行分部积分，有

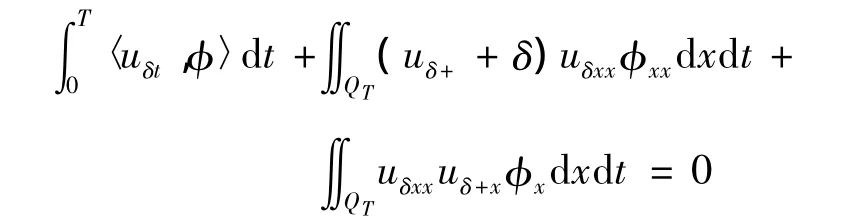
当δ→0时，可得到:

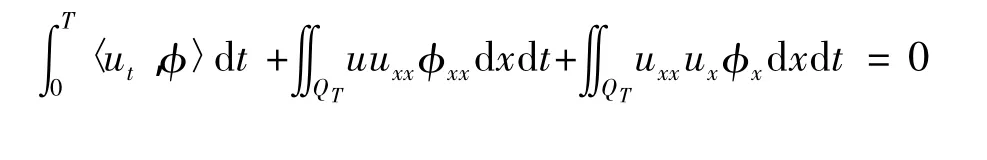
从而定理1成立.

3 结论

本文仅考虑了在非线性函数边界条件下，问题(1)～(4)解的存在性和正性.采用了熵泛函方法获得所需能量估计，进而引入新的熵泛函及检验函数来得到解的存在性和正性.然而对于薄膜方程还有很多值得研究的问题，希望感兴趣的读者加入到薄膜方程的研究工作中.

［1］BERNIS F，FRIEDAM A.Higher order nonlinear degenerate parabolic equations［J］.J.Differential Equations，1990，83:179－206.

［2］伍卓群，尹景学，王春鹏.椭圆与抛物型方程引论［M］.北京:科学出版社，2006.

［3］BOUTAT M，HILOUT S，RAKOTOSON J E，et al.A generalized thin － film equation in multidimensional space［J］.Nonlinear Analysis，2008，69:1268－1286.

［4］梁波，皇甫明，戴晓鸣.定态多维量子流体动力学模型解的存在性［J］.大连交通大学学报，2008，29(1):6－8.