火炮射击稳定性数值仿真

杜中华， 黄涛， 吴大林

（军械工程学院，石家庄050003）

火炮射击稳定性数值仿真

杜中华， 黄涛， 吴大林

（军械工程学院，石家庄050003）

为描述火炮射击全过程稳定性的时变特性，基于稳定性分析数学模型，采用数值仿真方法，给出了某型火炮射击过程中稳定力矩和翻转力矩的时变曲线。仿真表明，射击过程中全炮的稳定性呈现复杂的变化，尤其在复进阶段，火炮前翻和后翻趋势呈现交替变化的特征，另外，火炮射角对射击稳定性影响极大。

射击稳定性；数值仿真；数学模型

0 引言

随着近年来轮式火炮、车载火炮和超轻型火炮的迅猛发展，火炮轻量化趋势越来越明显。轻量化火炮的核心特性就是射击稳定性，这通常需要设计高效反后坐装置和炮口制退器来实现［1-3］。火炮射击过程中翻转方向要发生变化，因而稳定条件也要发生变化，另外翻转的驱动力（后坐阻力和复进合力）变化很复杂，这导致射击稳定性变化也十分复杂。本文针对某型地面火炮车轮着地射击的工况（稳定性问题最突出），基于后坐部分运动微分方程、射击过程稳定条件和稳定参量变化公式基础上的稳定性分析数学模型，对射击过程稳定性时变特性进行了数值仿真，重点考虑了后坐行程和火炮射角对稳定性的影响。

1 稳定性分析数学模型

该数学模型涉及内容较多，对火炮设计理论教材中已有内容只作简要介绍［4-6］，重点阐述教材中讨论较少或者没有涉及的问题，如后坐复进驱动力一体化描述、稳定参量变化公式等。

1.1 后坐部分运动微分方程

后坐阶段，

其中，V为后坐速度，R为后坐阻力。

其中，U为复进速度，r为复进合力。

在求解运动微分方程时，可将后坐和复进运动微分

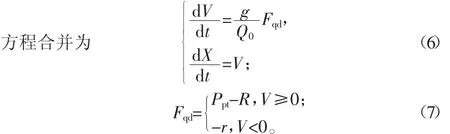
其中，V为后坐部分的速度，X为后坐部分行程。通过求解式（6），可以得到后坐部分在后坐和复进过程中的V和X，继而求得相关各力（如R、r等）的大小。这些力决定了火炮射击过程中的稳定性。

1.2 射击过程稳定条件

图1 后坐时全炮受力分析

将Ppt向惯性力作用线简化后，全炮受力情况如图2所示。后坐时火炮有绕驻锄后翻的趋势，其稳定条件为

其中，D为驻锄支点B到全炮重心的水平距离，h为R对驻锄支点B的力臂，e为后坐部分质心到炮膛轴线的距离，规定质心在炮膛轴线上方e为负，图中刚好是e为负的状态。

复进分为加速复进和减速复进两种情况，加速复进时期，全炮受力如图3所示。该受力情况与图2基本一致，只是Ppt·e＝0，R成为了r，其稳定条件仍然可以采取式（8）的形式。

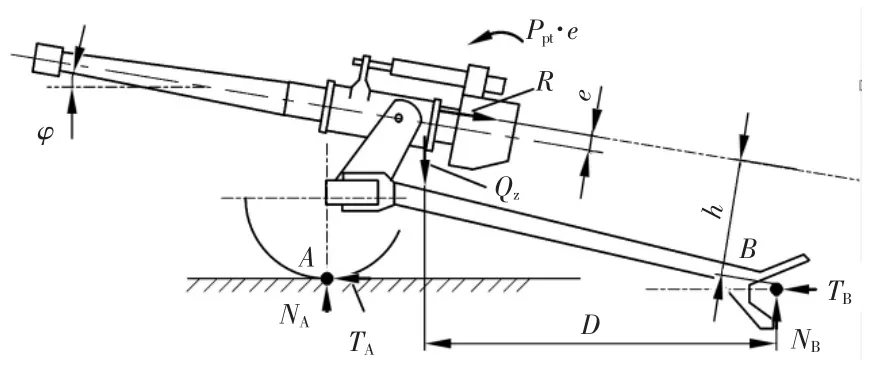
图2 后坐时全炮受力分析（简化）

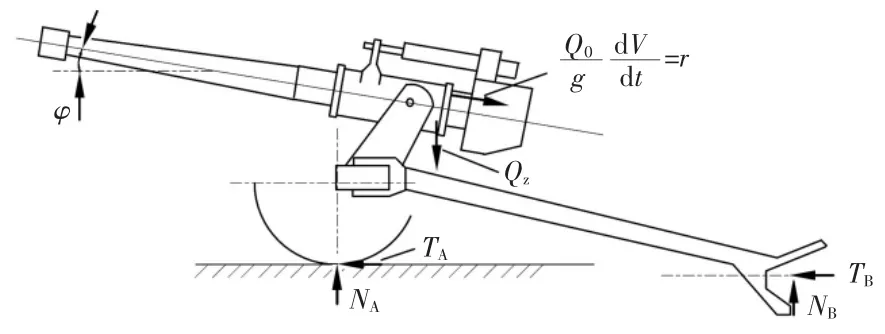
图3 加速复进时全炮受力分析

复进减速时期，全炮受力如图4所示。此时火炮有绕A点前翻的趋势，故稳定条件为

其中，L为车轮与地面接触点A到驻锄支点B的水平距离，hf为力r到A点的力臂。

图4 减速复进时全炮受力分析

总之，火炮射击过程中，稳定条件有两个，式（8）和式（9）分别对应火炮后翻和前翻两种情况，后翻时驱动力方向向后，前翻时驱动力方向向前，可统一用驱动力Qr来表征，后坐时驱动力为R，复进时驱动力为r。

1.3 稳定参量变化公式

射角变化和后坐行程变化时，稳定条件中各参数也要发生变化，这是研究稳定时变特性必须考虑的。

1.3.1 全炮重心随射角的变化

如图5所示，O为摇架耳轴中心，Lr为耳轴到驻锄支点的水平距离，C为火炮平射时火炮起落部分质心，C′为射角为渍时火炮起落部分质心，OC＝OC′＝l1；平射时，OC连线与水平线夹角为啄，射击前全炮重心到驻锄支点水平距离为D00；射角为渍时，射击前全炮重心到驻锄支点水平距离为D0，起落部分重量为Qq，则由图可知

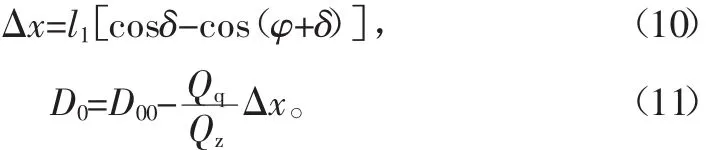
实际上，由于l1不大，射角变化后，全炮重心的变化很小。

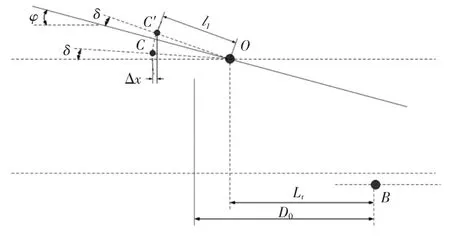
图5 全炮重心随射角的变化

1.3.2 全炮重心随后坐行程的变化

如图6所示，G为发射前后坐部分质心位置，G′为对应后坐行程X的后坐部分质心位置，则后坐行程为X时，全炮重力对B点的后翻稳定力矩为

图6 全炮重心随后坐行程的变化

后坐行程为X时，全炮重心对车轮与地面接触点的前翻稳定力矩为

1.3.3 力臂h随射角的变化

如图7所示，Hz为耳轴中心到地面垂直距离，驻H为驻锄支点B到地面垂直距离，由图可知，

1.3.4 力臂hf随射角的变化

如图8所示，L为车轮与地面接触点A到驻锄支点B的水平距离，由图可知

图7 力臂h随射角的变化

图8 力臂hf随射角的变化

2 某型火炮射击稳定性数值仿真分析

基于建立的稳定性分析数学模型，采用MATLAB语言编制程序［7］，可以得到某型火炮车轮着地射击时的稳定性时变特性（表现为稳定力矩和翻转力矩随时间的变化曲线）。

2.1 射角对稳定性的影响

射角20°射击时全炮驱动力Qr（后坐时为R，复进时为r）的变化如图9所示，由于复进时r较小，将其进一步放大。Qr为正时，全炮受力如图2所示，火炮有绕驻锄向后翻转的趋势；Qr为负时，全炮受力如图4所示，火炮有绕车轮向前翻转的趋势。图中椭圆虚线框内力的突然下降是由于后坐与复进的交替瞬间，阻力突然换向所致（参见式（2）和式（4））。复进过程中，有两个时间段Qr为正，两个时间段Qr为负，这说明复进过程中，火炮前翻后翻呈现一定的交替。

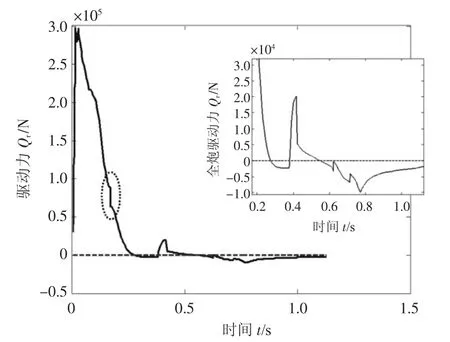
图9 射击过程全炮驱动力（射角20°）

射角20°射击时，稳定和翻转力矩如图10所示。力矩为正时，表示全炮有后翻趋势，力矩为负时，表示全炮有前翻趋势。整个射击过程，火炮2个阶段有后翻趋势，2个阶段有前翻趋势，与图9是对应的。由图10还可以看出，不同阶段稳定力矩在数值上（负数取绝对值）均大于翻转力矩，火炮能够保持稳定。但是不同阶段稳定程度变化很大，譬如，后翻趋势第二阶段的稳定性明显好于第一阶段。

图10 射击过程的稳定和翻转力矩（射角20°）

射角0°射击时，稳定和翻转力矩如图11所示，可以看出，后翻趋势阶段变为3个，且在后翻趋势第一阶段，翻转力矩大于稳定力矩，火炮不能保持稳定。该炮的稳定极限角为13°，故在射角0°射击，必然发生车轮跳起的现象。

图11 射击过程的稳定和翻转力矩（射角0°）

射角45°射击时，稳定和翻转力矩如图12所示，此时，后翻趋势阶段有2个，但是在这两个阶段，翻转力矩均变为稳定力矩，火炮不存在绕驻锄翻转的问题，这实际上是由于图2中翻转驱动力的作用线从驻锄右侧移到了驻锄左侧所致。

图12 射击过程的稳定和翻转力矩（射角45°）

2.2 火线高、驻锄长度及驻锄埋深变化对稳定性的影响

火线高、驻锄长度及驻锄埋深变化分别反映在参量Hz、Lr和驻H上。以射角20°射击为参照（图10），火线高降低20%、驻锄长度增加20%、驻锄埋深增加20%后的稳定力矩和翻转力矩分别如图13、图14、图15所示。可知，火线高降低和驻锄长度增加能显著提高射击稳定性，而驻锄埋深增加将导致射击稳定性有所下降。这些结论通常我们只是定性地了解，这里通过仿真可以给出量化的描述。

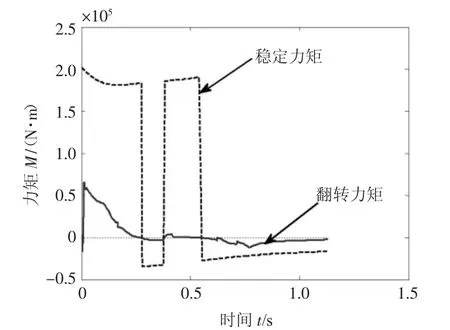
图13 射击过程的稳定和翻转力矩（射角20°，火线高降低20%）

图14 射击过程的稳定和翻转力矩（射角20°，驻锄长度增加20%）

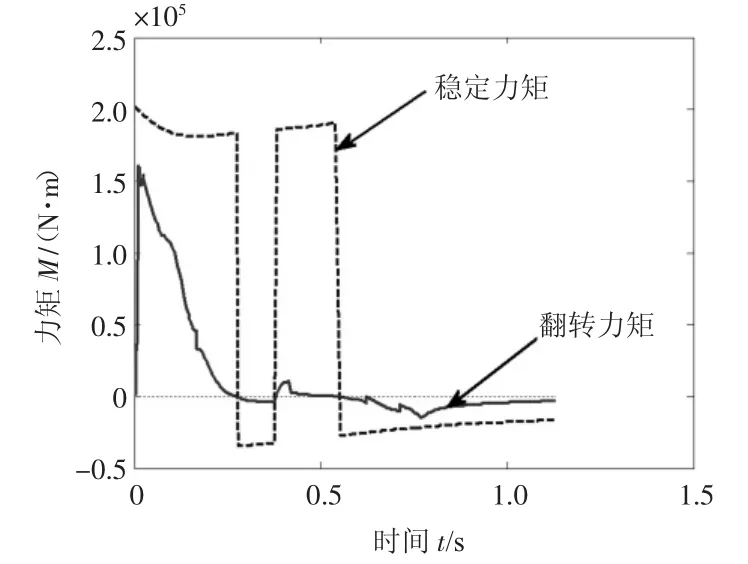
图15 射击过程的稳定和翻转力矩（射角20°，驻锄埋深增加20%）

2.3 后坐过程中Ppt·e对稳定性的影响

图16 后坐过程中附加矩对稳定性的影响（射角20°）

如式（8）所示，后坐过程中，Ppt·e（不妨称之为附加矩）对火炮稳定性有一定影响。Ppt数值很大，但是e值很小，附加矩Ppt·e对稳定性的影响大小却很难了解，通过仿真获得后坐过程中的翻转力矩和去掉附加矩的翻转力矩如图16所示。由于该型火炮后坐部分质心在炮膛轴线上方，e为负值，故附加矩将使翻转力矩变小。同时我们也发现，附加矩对翻转力矩影响并不是很大，或者说对火炮射击稳定性影响不大，这主要是由于Ppt作用时间很短，同时，附加矩在翻转力矩中所占比例很小。图中考虑附加矩的翻转力矩在曲线顶部的短期增大是因为这个阶段为后效期，该炮炮口制退器作用显著，弹丸出膛后，Ppt方向改变。

3 结论

火炮射击稳定性是火炮轻型化必须考虑的核心特性，通常我们对火炮射击稳定性的认识大都停留在定性的层面上，本文通过仿真获得了某型火炮射击全过程稳定性的时变曲线，为深入分析火炮射击稳定性提供了重要依据。

火炮射击过程中的稳定性表现出十分复杂的特征，主要原因是：驱动力变化复杂、翻转方向存在交替，稳定条件不断变化，稳定力矩和翻转力矩随后坐行程、射角、火炮结构参数发生变化。这些原因导致其数学模型十分复杂。

对某型地面火炮车轮着地射击时稳定性仿真结果表明：火炮射击过程中稳定性不断变化（表现为稳定力矩和翻转力矩的复杂变化）；射角对稳定性有较大的影响，火线高、驻锄长度、驻锄埋深对稳定性也有影响；Ppt·e对火炮稳定性影响不是很大。

［1］ 谈乐斌，候保林，陈卫民.降低火炮后坐力技术概述［J］.火炮发射与控制学报，2006（4）：69-72.

［2］ 余子平，钱林方，徐亚东.基于动力学仿真的车载火炮射击稳定性优化［J］.火炮发射与控制学报，2006（3）：36-40.

［3］ 宗士增，钱林方，何永等.轻型车载火炮二维后坐动力学研究［J］.弹道学报，2006，23（2）：76-78.

［4］ 高树滋，陈运生，张月林，等.火炮反后坐装置设计［M］.北京：国防工业出版社，1995.

［5］ 张相炎，郑建国，扬军荣.火炮设计理论［M］.北京：北京理工大学出版社，2005.

［6］ 高跃飞.火炮反后坐装置设计［M］.北京：国防工业出版社，2010.

［7］ 薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用［M］.北京：清华大学出版社，2002.

（编辑：启 迪）

Numerical Simulation of Gun Fire Stability

DU Zhonghua,HUANG Tao,WU Dalin
（Ordnance Engineering College,Shijiazhuang 050003,China）

To describe the time-variation character of gun fire process stability,the stability analysis mathematic model are built,certain gun's time-variation curve of stable moment and overturn moment during fire process were obtained through numerical simulation.The research indicates that gun fire stability is fluctuant,gun's overturn direction is changing during counter-recoil phase,and fire angle has a big impact on fire stability.

fire stability;numerical simulation;mathematic model

TP 391

A

1002－2333（2014）04－0097－04

杜中华（1973—），男，博士，讲师，研究方向为系统仿真和优化设计。

2014-01-21