我国股权风险溢价的长期趋势与短期特征——结合门限自回归模型与B－P多重结构型断点检验的经验研究

郑晓亚

（中国建设银行股份有限公司资产负债管理部，北京 100033）

我国股权风险溢价的长期趋势与短期特征
——结合门限自回归模型与B－P多重结构型断点检验的经验研究

郑晓亚

（中国建设银行股份有限公司资产负债管理部，北京 100033）

经过20余年的高速扩张，我国证券市场建设在取得可喜成就的同时，市场的发展与改革已进入“深水区”。如何在准确找出问题的基础上有的放矢地推进市场改革，成为监管层与学界关注的焦点。以股权风险溢价为切入点，透视我国证券市场的发展历程，通过定量研究明确我国市场的特征，为找出发展过程中的问题与不足奠定基础。研究发现：从整体来看，我国溢价的算术均值较高，但各年度的溢价水平起伏不定。在多数年份，我国证券市场金融资产的风险与收益出现错配，市场高溢价与高波动性并存。从溢价的长短期趋势来看，我国的长期股权风险溢价在统计意义上数据序列平稳，存在与西方成熟市场国家相似的均值回归趋势；但影响溢价的结构性突变因素仍显著存在，局部溢价特征与我国宏观经济的稳健增势呈背离之势。

股权风险溢价；门限自回归模型；B－P多重结构型断点检验

一、引 言

证券市场，是一种通过价格信号来配置资源的市场机制，价格机制的合理性和有效性直接决定了其资源配置能力，而价格机制的扭曲将直接导致资源配置的低效甚至无效。证券市场最基本的作用之一即在于优化资源配置，其资源配置功能的有效发挥是实现促进储蓄向投资转化、创造流动性、分散和降低市场风险等功能的前提条件。在理想的市场经济条件下，一个运作良好的证券市场应在市场价格这个指挥棒下实现社会资源的合理配置。证券市场综合了社会上大大小小的各类行业，任何一个行业的发展状况都应该能够在证券市场上得到体现。所以，股票市场是国民经济的晴雨表，它的表现在很大程度上代表了整个社会的经济发展状况。反之，一个扭曲的证券市场不但对国民经济发展起不到晴雨表的功能，而且不能合理地实现全社会的资源配置，造成的是资源的浪费以及资源的扭曲配置。

纵观我国以股票市场为代表的证券市场历史沿革，可发现在短短20余年的时间里我国已取得了突飞猛进的发展。一方面市场规模不断扩大，直观反映为A股上市企业数量高速增加；另一方面股票市场的社会影响力不断提升，A股开户数量一直以来基本保持稳定的增势。但值得关注的是，我国证券市场的建立源于大规模的制度推进，其在建立之初的根本目的在于为国有企业的生存发展筹措资金，而并不是为了促进资源在普通民众和企业间进行有效的分配。所以，从市场设立的初衷来看，我国证券市场存在制度性的缺陷。近年来，随着证券市场规模和社会影响力的不断扩张，决策者们开始重新审视市场在整个国民经济当中应有的作用和地位，提出发展市场的思路应回归资本市场的基本功能，加强市场基础性建设，优化资源合理配置，充分发挥资本市场服务国民经济全局的功能①见国务院［2004］3号文件《关于推进资本市场改革开放和稳定发展的若干意见》及尚福林2009年在中国金融论坛的发言《发挥资本市场服务经济功能》。。在发展思路出现重大转变的背景下，深入探讨我国证券市场的价格形成机制是否合理、资源是否得到了有效的配置，既是我们调整思路、深化改革所必须了解的重要问题，也是我们针对现存不足，有的放矢、对症下药的先决条件。

股权风险溢价，是以股票为代表的股权风险资产收益率与无风险资产收益率的差额。从现代微观金融的基本原理来看，风险溢价的内涵是投资者投资于风险资产所要求的超额回报，这一超额回报源自风险。由于证券市场价格形成机制同样直接源自风险与收益原理，由此，研究该机制的一个合理切入点即是股权风险溢价。本文以我国股票市场设立以来的股权风险溢价作为核心研究对象，寄希望于以一个较为前沿的视角透视我国资本市场的发展历程，通过定量研究明确我国市场的特征，为定位那些发展过程中的问题与不足奠定实证研究基础。

表1 1992－2012年我国年度股权风险溢价测算结果

二、我国股权风险溢价的测算

国内研究由于采用的方法和测算区间存在差异，故针对我国股权风险溢价得出的测算结果大相径庭。如杜海凤、王晓婷［1］在利用上证、深证股票综合指数作为股权风险资产收益率替代指标的基础上得出1991年至2008年间上证溢价为30．044%，深证溢价为27．256%；廖理和汪毅慧［2］衡量了我国1997年到2001年间的A股市场的股权溢价水平，首先在美国市场溢价的基础上测算出的我国的相对溢价水平为6．38%，其次分别利用1年期国债回购利率和1年期定期存款利率作为无风险利率，得出的溢价水平分别为6．78%和8．29%；程兵、张晓军［3］利用Nelson-Siegel远期利率模型估计1年期国债收益率作为无风险资产收益率的替代变量，并分别采用盈利增长模型、股利贴现模型和几何平均法测算我国1997年至2001年的股权风险溢价，得出－18．07%至9．22%之间的溢价均值水平。本文在前人研究的基础上综合考虑数据的可得性与测算方法的合理性，具体用以下方法进行指标选取，对年度和月度溢价水平进行了衡量。测算结果的年频数据如表1所示。

在股权风险资产收益率的测算方面，首先将测算期间分为1992年1月至1999年12月和2000年1月至2012年12月两个部分：对第一个研究区间，利用CSMAR数据库的A股市场样本股收益率作为股权风险资产收益率的替代指标；第二研究区间以申万A股指数为基础得到股权风险资产收益率。在无风险资产收益率的测算方面，以2004年6月国债回购市场建立并真正存在大量短期国债的活跃交易的时点为界，选取1992年1月至2004年6月的定期存款利率作为无风险资产收益率的替代变量；而2004年6月以后的无风险资产收益率则选择比定期存款利率更具代表性的银行间国债回购利率作为其替代变量。首先从WIND数据库中选取其中R6M及以上期限的产品得到相应的月度收益率①月度数据以日回购利率为基础加权计算得到。，其次用月交易量进行加权得到债券回购市场的加权收益率。

从测算结果可以发现，我国年度股权风险溢价的算术平均和几何平均水平均为正值，代表就本文选取的股权风险资产和无风险资产的收益率而言，风险资产收益率在研究区间内超过无风险资产收益率。整体而言，我国IPO新股对于投资者而言供不应求［4］。但就具体的数据结构来看，我国的溢价水平起伏不定，随时间变化的幅度较大。尽管全部年份股权风险溢价的算术均值为16．53%，部分年份超额收益率达到100%以上，但在所有的21个数据中，负值占50%以上。表明在大多数年份，我国投资者持有A股指数的年度收益率尚不及他们通过持有债券或1年期定期存款获得的收益率。

月频数据的时序图如图1所示。可以发现，我国资本市场在运行初期波动剧烈，其中部分月份甚至出现超过150%的股权溢价，底部则超过－30%。1996年以后，超过50%以上的月度巨幅涨跌不再出现，尽管波动依旧持续，但相对而言波动幅度已呈缩减趋势，整体走势已从极端趋向相对平稳。

进一步借助描述性统计，得到股权风险溢价整体序列的数据特征。如表2所示，溢价月频数据全局样本的均值为1．49%；标准差为16．11%。数据序列中股权风险溢价峰值达到150．38%，出现在1992年5月；谷值位于1994年7月，当月跌幅达到－33．14%，由此，整体数据的极差达183．52%。此外，偏度为4．70，序列分布呈正偏态，一方面代表样本均值大于所有股权溢价数据的中位水平，另一方面显示绝对股权溢价水平高于样本均值1．49%的月份数量要多于样本均值以下的月数。此外，峰度达到38．70，厚尾特征尤为突出，代表我国的历史股权溢价水平就整体而言并不在一个相对固定的范围内波动，且极端值出现的概率较大；此外，由于峰度值大于3，数据序列的分布形态比正态分布更为陡峭。

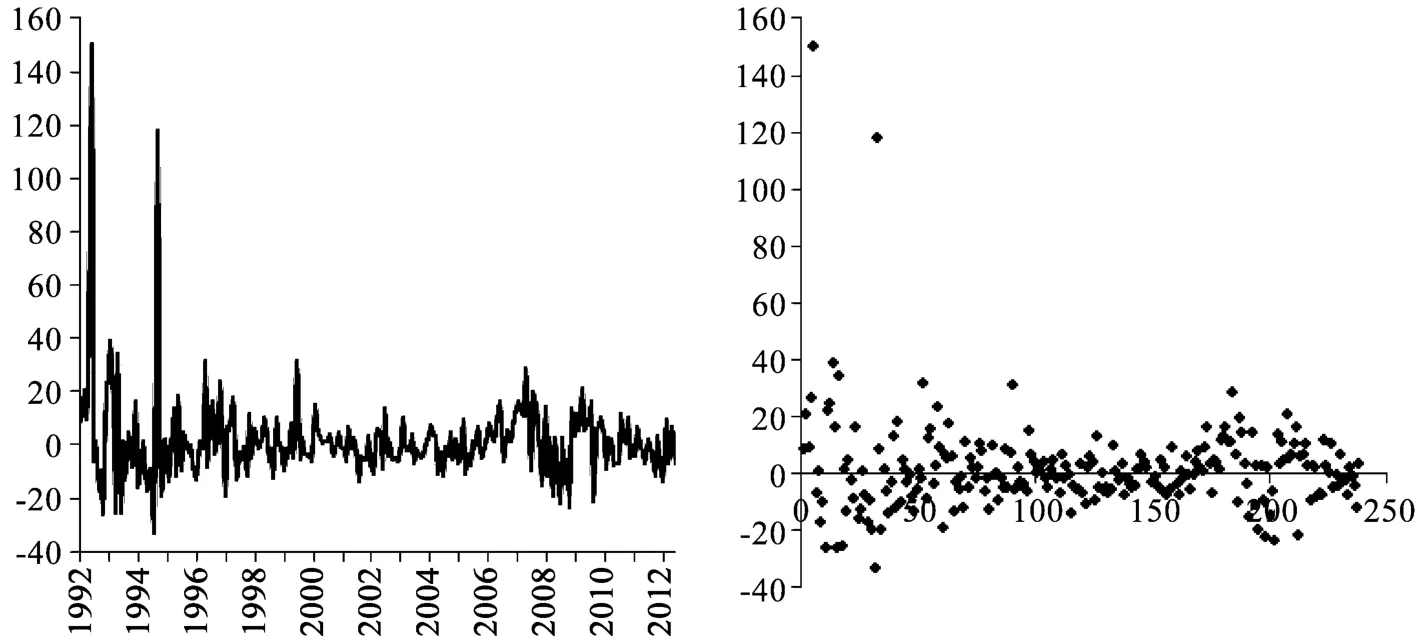
图1 股权风险溢价月度数据时序图和散点图（全局样本）

表2 股权风险溢价月度数据的描述性统计（全局样本）

三、我国股权风险溢价的长期趋势判析

前文通过描述性统计的方法在一定程度上得到了长期趋势的特征信息，这一部分借助较新的统计分析方法进一步研究我国股权风险溢价的整体特性：首先，分析我国溢价的历史水平对未来水平是否存在预测作用，且这一潜在的序列内生性调整是否呈一个线性的过程；其次，在完成线性判别后，利用相应的检验方法探寻该调整过程是否具备统计意义上的平稳性；进而探讨我国市场的溢价水平是否与西方市场一样，存在一个长期的均值回归趋势。

就如上分析目标，传统的研究方法多先验性地假设序列遵循一个线性过程，借助线性平稳性检验，如DF、ADF、PP等方法来完成。随着计量分析技术的发展，近年来开始出现采用非线性的计量方法对时间序列的平稳性进行研究的文献。国外在非线平稳性的实证研究中，大量文献围绕购买力平价成立与否的讨论展开，如Kapetanios等［5］，Kilian和Taylor［6］等运用非线性方法发现了长期购买力平价存在的证据。而针对资本市场的实证文献并不多见，较具代表性的是Narayan［7］利用非线性的方法研究澳大利亚和新西兰股票市场，得出两国市场股指序列存在非线性调整过程，但序列本身不具备平稳性的结论。在这些文献中，尽管多数的研究领域与本文研究不尽相同，但其方法无疑可为本文研究所借鉴。

笔者通过回顾这些文献发现，采用不同的非线性方法得出的结论间存在较为显著的差异。部分研究存在的共同问题是无法在非线性和非稳态之间进行区分，故仍然采用线性研究中广泛使用的传统检验方法对存在非线性关系的序列平稳性进行检验。考虑到如上问题的普遍性，本文采用最新发展起来非线性门限自回归模型和相应的非线性单位根检验方法，在首先判断时间序列存在线性还是非线性关系自回归过程的基础上，结合判断结果采用相应的方法对序列进行检验，旨在得到更为合理、稳健的检验结果和分析结论。

（一）检验方法

结合Caner和Hansen［8］提出的门限自回归模型（Threshold Autoregression Model）的一般形式与本文的研究对象，得到如下两区制TAR（k）模型：

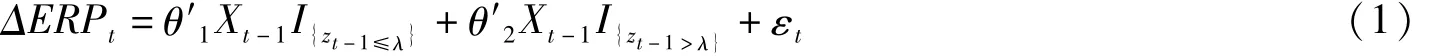
如上模型中，Xt－1＝（ERPt－1，1，ΔERPt－1，…，ΔERPt－k）′；其他变量含义为：ERPt代表被检验的我国股权风险溢价月度数据，其中t＝1，…，T；εt是满足独立分布的随机误差项；k代表自回归阶数，满足k≥1；zt－1＝St－1－St－m是阈值变量，其中任意滞后阶数m≥1；λ代表阈值参数，作为未知变量，使ERPt随阈值变量Zt－1＝St－1－St－m在两种区制间进行转化；I代表指标函数，当Zt－1≤λ时，I＝1；相反，当Zt－1＞λ时，I＝0；而向量θ1与θ2则分别为：

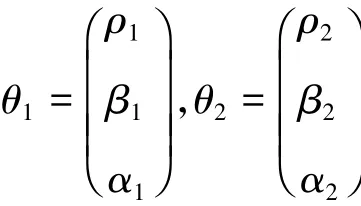
其中，ρ1和ρ2为标量，代表ERPt－1的斜率系数；β1和β2是以标量形式存在的截距项，且二者的值同为1，代表确定性部分的斜率；α1和α2为1×k向量，代表（ΔERPt－1，…，ΔERPt－k）在两个区制中的斜率系数。

为得出最终估计值，利用最小二乘法对模型中的不同滞后期数的变量进行多次估计，通过比较Wald统计量得到最优滞后期数m*。在此过程中，未知变量λ∈［λ1，λ2］，λ1、λ2服从Pr（Zt≤λ1）＝π1，Pr（Zt≤λ2）＝π2。其中，0＜π1＜π2＜1，且π1＋π2＝1。

向量θ1和θ2中每一个参数的估计值可通过如下公式的最小化得出：

上式中，t＝1，…，T。给定λ和m并使用最小二乘法，得到残差的估计值＾εt（λ，m）。由此，阈值变量的估计值可通过下式得到：

利用标准的Wald统计量，可对阈值进行检验：WT＝WT（＾λ）＝supλ∈［λ1，λ2］WT（λ），Wald检验的零假设为：H0：θ1＝θ2。如果不拒绝零假设，即代表序列没有门限效应，股权风险溢价序列服从线性变化。如拒绝零假设，则代表股权风险溢价序列存在门限效应，调整过程为非线性。同时，supλ∈［λ1，λ2］WT（λ）服从非标准分布，Caner和Hansen［9］建议采用自抽样法以得到其渐近的临界值和P值。

进一步，如果股权风险溢价序列服从非线性过程，应相应地利用非线性单位根检验的方法对序列平稳性进行检验，这里应用完全单位根检验法和部分单位根检验法。结合如上构建的TAR模型，其判断标准为：如接受零假设H0：ρ1＝ρ2＝0，则代表两个区制均包含一个单位根，股权风险溢价序列在两个区制中均不遵循一个平稳的过程；如拒绝零假设H0，则代表序列服从平稳过程，数据序列从长期来看存在均值回归趋势。两个区制均存在单位根的备择假设为：H1：ρ1＜0且ρ2＜0。如单一区制下存在单位根，备择假设可被重新构造为：H2：ρ1＜0且ρ2＜0，或ρ1＝0且ρ2＜0。如接受备择假设H2，则一个区制的数据序列存在单位根，而另一区制下的样本平稳且存在均值回归趋势。

具体而言，门限单位根检验通过构造两个Wald统计量进行，即：

其中，S1，T代表单侧检验统计量，与备择假设ρ1＜0或ρ2＜0相对立；而S2，T是双侧检验统计量，与备择假设ρ1≠0或ρ2≠0相对立；t1与t2分别是估计值＾ρ1和＾ρ2的比率。

（二）检验结果

笔者在这一部分研究中使用的统计分析软件为Matlab 7．11．0。结合本文的研究目的对标准程序进行调整，具体设置包括差分序列滞后期设定为12，自抽样次数设定为300。在本文股权风险溢价序列全局样本数据的239个观测值中，整体得到区制1中的观测值35个，占比接近15%，区制2中观测值数量为204，占全局样本的85%。

第一步，在门限自回归模型的设定下，结合两个区制中的样本，利用最小二乘法对上文设定的TAR模型进行估计，结果如表3所示。

可发现，除截距项和一阶滞后变量外，滞后差分变量中滞后一期的DERPt－1的估计值尤为值得关注，具体而言：在样本数量较少的区制1中，估计结果为0．6255，在样本数量占85%左右的区制2中，相应的估计值为－0．3065；在显著性检验结果出现之前，仅就估计结果而言，其代表相对短期的历史溢价水平对即期溢价水平具备较为明显的预测作用。并且在模型的不同区制中，预测的作用方向存在差异，其表征估计值的符号在区制间出现反转。此外，从DERPt－1到DERPt－5估计值变动的情况来看，在区制1中，预测的作用程度随滞后期数的增加不断减弱；而就区制2而言，DERPt－1和DERPt－2的估计结果显示，其与即期指标的关系更强一些。

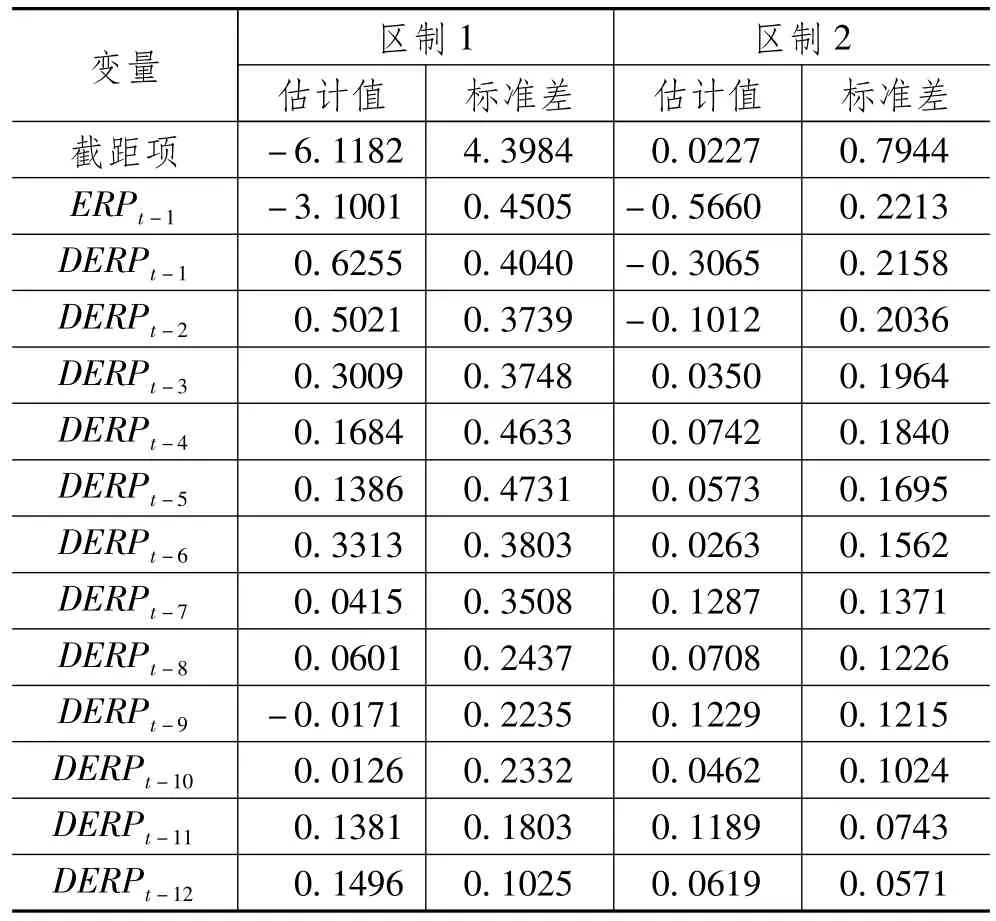
表3 TAR模型的最小二乘估计结果（全局样本）

第二步，在估计结果的基础上，一方面检测各估计量的显著性水平；另一方面在Zt－1＝rt－1－rt－m中寻找最优滞后期数，并检测股权风险溢价月度数据序列在固定滞后参数的设定下是否存在门限效应。表4汇报了截距项以及各滞后项估计值的显著性，以及Wald检验的结果。由表3首先可知各滞后量估计值多数显著。通常以0．05为标准，则除滞后4期和9期以后的部分估计量以外，其余显著。进一步，可得到前文所述的最优延迟期数m*，由于笔者设定的检验最大滞后期数为12，故m*的取值范围在1到12之间。可以发现，当m＝1时，该延迟期数中的滞后变量DERPt－1是使非线性自回归模型中利用最小二乘估计得到的残差的方差和最小的变量，该期相应的Wald统计量WT取值与其他滞后期数的统计量相比最大，故股权风险溢价序列的最优滞后期数m*为1。该期的Wald统计量为85．6134，在1%的显著性水平下，临界值为72．8683。由于Wald统计量在最严格的显著性水平下大于临界值，故可拒绝零假设，认为最优滞后序列在固定滞后参数下的门限检验中显示其存在门限效应，一阶差分滞后变量与t期变量之间为非线性的调整过程。

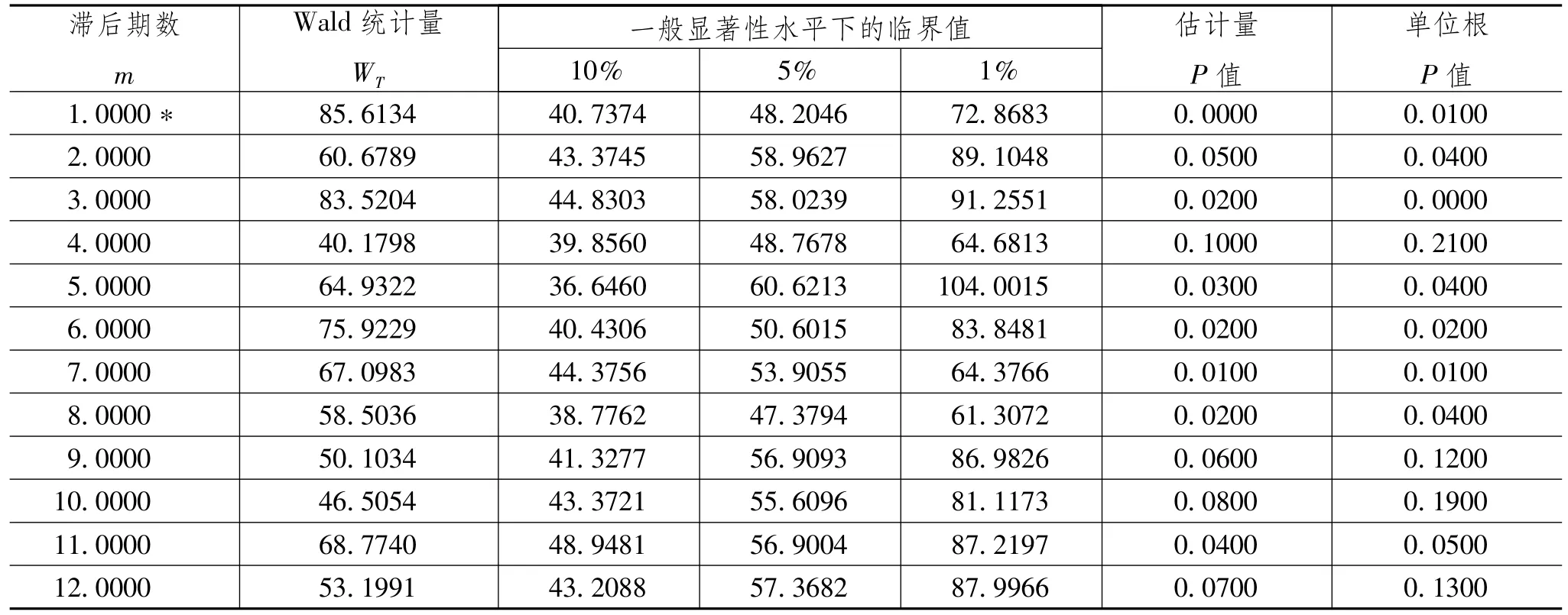
表4 设定固定滞后参数的门限检验结果（全局样本）

进一步，在估计滞后参数设定下对最优滞后期进行门限效应检验。表5汇报了这一检验的结果。在滞后参数为估计值时，统计量在1%的显著性水平下的临界值131．7353大于Wald统计量85．6134，但在5%和10%的显著性水平下，与固定滞后参数下的检验结果一致。结合表3与表4的检验结果，就整体而言，可认为序列在5%的显著性水平下存在门限效应。其次，由于最优滞后期数的估计量P值在两种检验设定下均满足通常的显著性判别标准，可认为最优滞后期下的估计值是显著的，估计结果可作为判断历史溢价水平对未来水平的预测效应的依据。

表5 估计滞后参数设定下的门限检验结果（全局样本）

第三步，由于序列的自回归调整过程更多地体现出非线性特征，故相对于ADF、PP等传统方法，利用非线性的单位根检验方法能够更为稳健地发现序列是否存在单位根。如前文所述进行单侧的单位根检验，可借助统计量S1，r与临界值的比较判断是否存在单位根。检验结果如表6所示。

从表6中可发现，部分滞后期中，在1%的显著性水平下不能拒绝零假设。重点考察前面找到的最优滞后期m*＝1，Wald统计量S1，r为53．8893；在10%、5%和1%的显著性水平下，临界值分别为10．0597，12．2250和15．7408，均小于Wald统计量，故拒绝存在单位根的零假设，序列在严格的显著性水平下不存在单位根，在非线性单侧单位根检验下序列体现出平稳性。

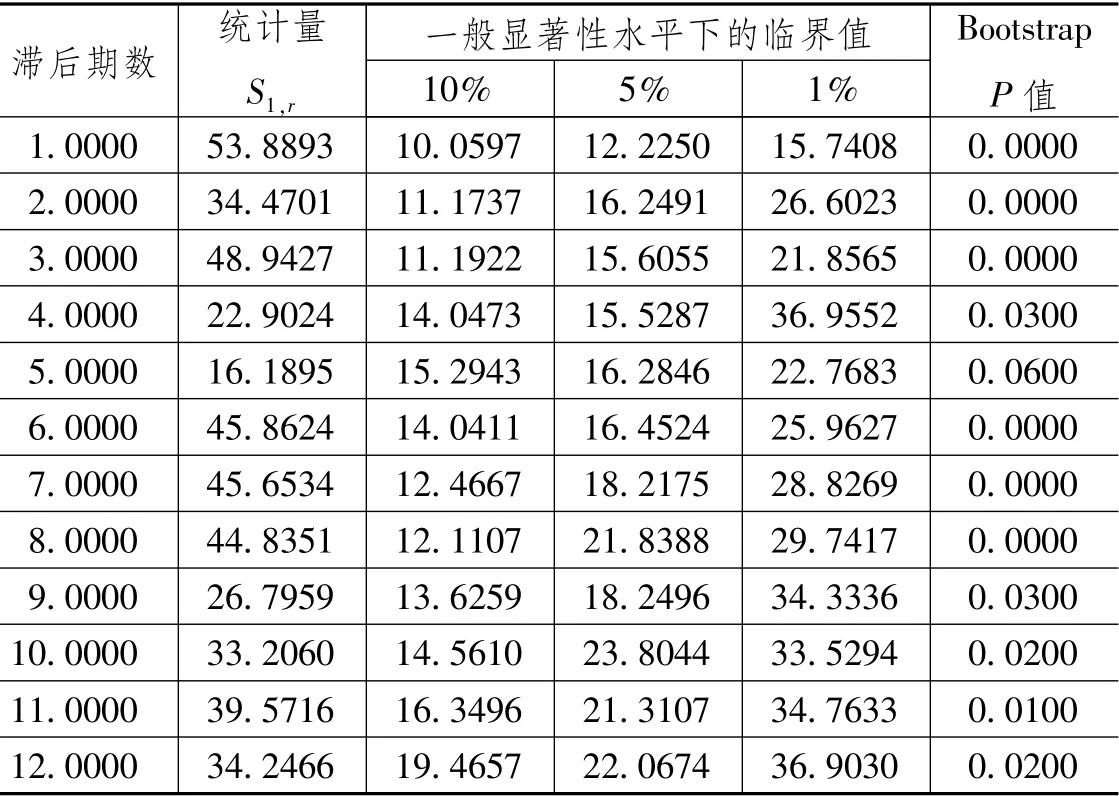
表6 非线性单侧单位根检验结果（全局样本）

（三）长期趋势的特征分析

通过以上的检验结果，可得到更多关于我国股权风险溢价长期趋势的信息：

第一，门限自回归模型的实证结果显示，在所有差分项中，一阶差分滞后变量的估计值最大且显著，代表我国股权风险溢价的当期水平与其历史水平，尤其是最近一期的水平存在较为显著的关系。仅就序列内生性考察而言，这代表我国的股权风险溢价受相对短期的历史溢价信息的影响较大；如考虑外生因素的影响，在序列自我调整显著存在情况下，外生冲击对序列产生的正负反馈效应会呈放大趋势。此外，根据Fama提出的有效市场假说，在弱式有效的假设下可认为即期市场价格能够充分反映所有过去历史的证券价格信息［10］。有效市场假说的实证检验，特别是弱式有效的检验争议较大且方法较多。本文利用的序列自回归检验对这一问题的解释基础在于，如果股票价格的升降对后来的价格变化存在某种影响，那么在时间序列上应表现出某种自相关关系。由于本文检验的股权风险溢价信息更多地来自于股票市场，故本文研究成果也可为我国股市是否弱式有效间接地提供一份新的事证。

第二，在前文针对股权风险溢价的分析检验中，其自回归过程服从线性还是非线性，是进行平稳性检验前首先探讨的问题。门限效应的检验结果显示，我国股权风险溢价的内生调整过程更多地体现出了非线性的特征。结合门限自回归模型得出的Wald统计量和临界值的比较，本文认为股权风险溢价的当期水平与最近一期的水平之间存在非线性的关系，自回归的调整过程并不满足简单的线性叠加原理。笔者对这一过程的经验判断是，由于股票市场是经济系统的一部分，其调整过程一方面在时间上存在不可逆性，另一方面受多重因果反馈和大量不确定性因素的影响，其调整的机理尤为复杂，不能够以简单的线性关系进行概括。

第三，非线性单位根检验的结果显示，我国股权风险溢价的全局样本序列不存在单位根，代表序列具备平稳性。与第一、二点结论相结合，显示长期序列服从非线性平稳过程，我国长期的风险资产超额回报率存在均值回归的趋势。由于方法上的改进，本文得出的这一论断与其他采用线性方法检验非线性过程的研究相比无疑更趋稳健，且与Dimson、Marsh和Staunton［11］对世界市场的长期考察得出的结论相比基本一致。

四、我国股权风险溢价的短期结构分析

通过前面的研究结果可以发现，我国股权溢价水平就整体而言具备一定的稳定性特质，但在相对稳定的长期趋势中仍不能排除短期波动及分段趋势差异的存在。如需进一步深入研究数据序列中隐藏的各类波动因子，需要对包含在长期趋势中的短期特征进行分析。各类研究通常采用的方法之一是将整体样本划分为不同的子样本，在此基础上考察整体数据的结构性特质。而如何以时间为标准选取样本区间，无疑是在进行这类分析研究前首先需要考虑的问题。

（一）B－P多重结构型断点分析

分割全局样本，传统的方法是借助趋势图，找出其中较为明显的拐点；或借助事件分析，找出对样本序列影响较大的事件发生的时间点，以此作为序列结构性的突变点。笔者发现，为数不少的研究文献直接利用主观选定的时间点作为研究区间的划定依据；而部分研究则在此基础上进一步运用结构性断点测试的方法检验自己选择的结构性断点是否在统计意义上具备合理性。笔者认为，如上研究方法至少存在两个较为显著的问题：其一，在样本区间的选择上存在主观性，错误定位断点的可能性较大，且从严格意义上来说，断点搜寻需耗费研究者大量的精力；其二，采用Chow检验，［12］Cusum检验［13］等早期的结构性突变检验方法只能对一个断点进行检验，故从其统计意义上来说样本区间只能分为两个（Zeileis等［14］），不能保证对波幅较大且波动频繁的时间序列进行有效的区隔。

笔者通过回顾国外研究发现，西方学者们持续不断地尝试对结构性断点检验进行改进，Bai和Perron［15，16］）提出的检验方法是其中较为成熟的研究之一，其不仅能够排除传统方法中的主观先验因素，发现时间序列中的未知断点；还能够构造统计量对多个结构性断点进行检验和比较。多重结构性断点检验（简称B－P检验）的思想首先是构造个断点的多重线性回归模型：

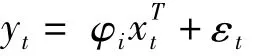
其中，t＝Ti－1＋1，…，Ti；yt代表B－P构造的t期因变量取值，N代表样本数量，xTt是t期的协方差自变量的向量；φi代表回归系数向量；T代表结构性断点，则满足Tm＋1＝T，T0＝0；εt代表随机扰动项。研究者需要假定最大的断点数量，这里以m*代替，B－P检验法的目标是在m*≥m≥0的范围内，通过计算如上回归模型的残差和并找出最小值，选定结构性断点的数量m和断点在时间维度中相应的位置Ti（i＝1，2，…，m）。

Bai和Perron［15］利用Gauss软件定义检验过程并成功得出了实验结果；国内学者程刚，张珣和汪寿阳［17］利用这一程序对我国能源生产的时间序列进行了实证分析。从程序应用的角度出发，Zeileis等人结合不同的数据案例，在基于S语言编制的R软件环境下模拟了B－P检验法，并在与原始Gauss程序比较的基础上对自己的程序进行了多次改善。本文利用Zeileis等人于2012年5月最新升级的Strucchange程序包，找到我国月度股权风险溢价序列的结构性突变点，并据此分段样本区间，以期得到更为严谨和稳健的实验结果。

在B－P检验的数据选择上，由于股权溢价水平波动较大，且大量数据为负值，难以对其进行对数平滑处理，故直接利用月度股权溢价数据进行检验或难以得到有效的结果。相比较而言，市场指数更具可操作性。一方面，市场指数作为一种衡量市场价格的数据，不仅皆为正值，作为替代变量也能够对趋势进行衡量。另一方面，由于无风险资产收益率在很长一段研究区间内缺乏数据弹性，且其绝对水平较低，故对股权溢价的影响较小。笔者综上认为，市场指数能够作为股权溢价月数据在B－P检验中的合理替代。

进一步，借鉴Zeileis等［14］的程序参数设定方法，将回归方程的独立变量定为1，令最小分段数量为15，此时全局样本中至多允许存在5个结构性断点，即m*＝5。此外，考虑在时序图中1996年1月以前的波动过大，故将其排除出检验范围，并单独进行讨论①笔者也实际将1996年1月以前的数据纳入检验范围进行了实验，发现这一阶段的波动对检测结果的异常影响较大。。在对剩余204个指数月度数据经平滑处理后进行B－P检验，得到检验结果如表7。从表中可以发现，断点数量取为3个时的检测结果与其他结果相比较为合理。其对应断点按时间先后顺序排列的数据位置i分别为：67，119和162，可据此找到断点对应的时间点Ti，其中T67为2001年7月；T119为2005年11月；T162为2009年6月。加上1995年12月这一先验断点，本文找出的结构性断点共有四个。

根据B－P检验法得到的这三个断点，加上1995年12月这一先验断点，本文将全局序列划分为5个子区间，第一区间SR1为1992年1月至1995年12月；第二区间SR2为1996年1月至2001年7月；第三区间SR3为2001年8月至2005年11月；第四区间SR4为2005年12月至2009年6月；第五区间SR5为2009年7月至2012年12月。

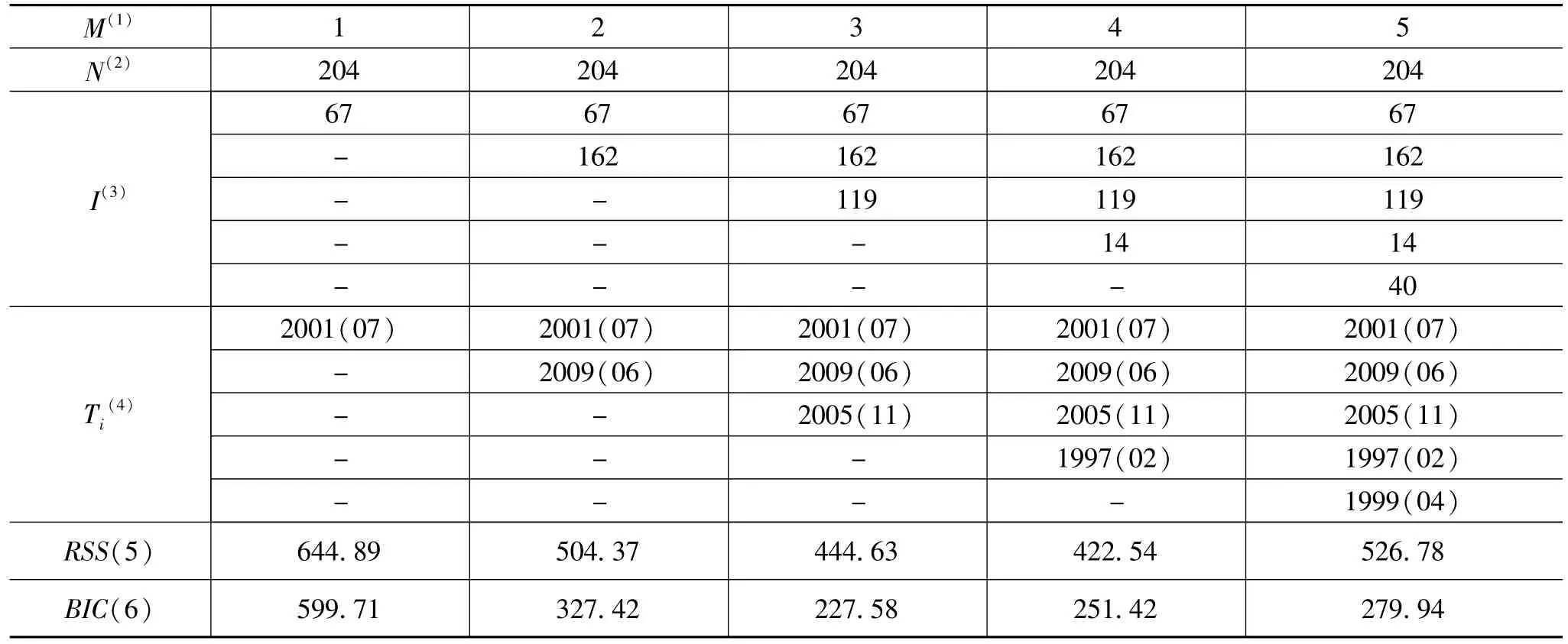
表7 月度股权溢价数据序列B－P结构性断点检验结果（全局样本）

（二）分段样本区间的描述性统计分析

除主观选取的断点之外，通过B－P检验法得到的其他结构性断点分割出的样本区间从理论上来说能够体现出不同的统计特征。表8汇报了各分段样本数据的描述性统计结果。

首先，由于以百分比形式表示的收益率不存在量纲和单位问题，故以标准差和极差作为判断相对波动性的替代指标。笔者先验得到的样本区间SR1代表1992年1月至1995年12月，这一区间内的沪深两市成立伊始，与其他样本区间相比这一时段的股权风险溢价水平具备最强的波动性，标准差达到31．97%，区间内的波动范围为183．52%也是各区间中的最大波幅。此外，由于该区间标准差超过全局样本标准差接近一半，而其他区间标准差值均显著小于16．11%，由此可判断，整体股权风险溢价的波动性在很大程度上受到1992年1月至1995年12月间波动性的影响。以同样标准来判断，代表2001年8月至2005年11月的样本区间SR3无疑走势相对平稳，标准差为5．74%，极值范围也小于其他区间，区间内的极大值仅为13．59%，极小值为－11．77%，这一时段月度股权风险溢价的波动稍缓。

表8 各样本区间股权溢价月度数据的描述性统计（分段样本）

其次，通过结构性断点分段得到的各样本区间的峰度值与表2中全局样本的38．70相比小得多。其中，先验的第一区间样本峰度仍超过10，代表极端值出现的概率仍然较大，厚尾度已有所降低。就其他区间来看，样本分段的修正效力更强，峰度值在－0．11至2．03之间，分布形态较为平坦。

最后，各样本区间均值的符号存在差异，且月度股权风险溢价的算术平均水平高低不一。其中SR1、SR2和SR4为正值，投资者在这些时段投资股权风险资产，平均而言能够获得比无风险资产高的额外溢价。而SR3和SR5区间均值为负，由于溢价水平更多由风险资产收益率决定，或代表在这些区间我国A股市场走低。但借助描述性统计中得出的均值来判断，无疑缺乏一定的严谨性，笔者利用市场指数生成了各区间的时序图，希望能够据此佐证描述性统计中得出的判断。

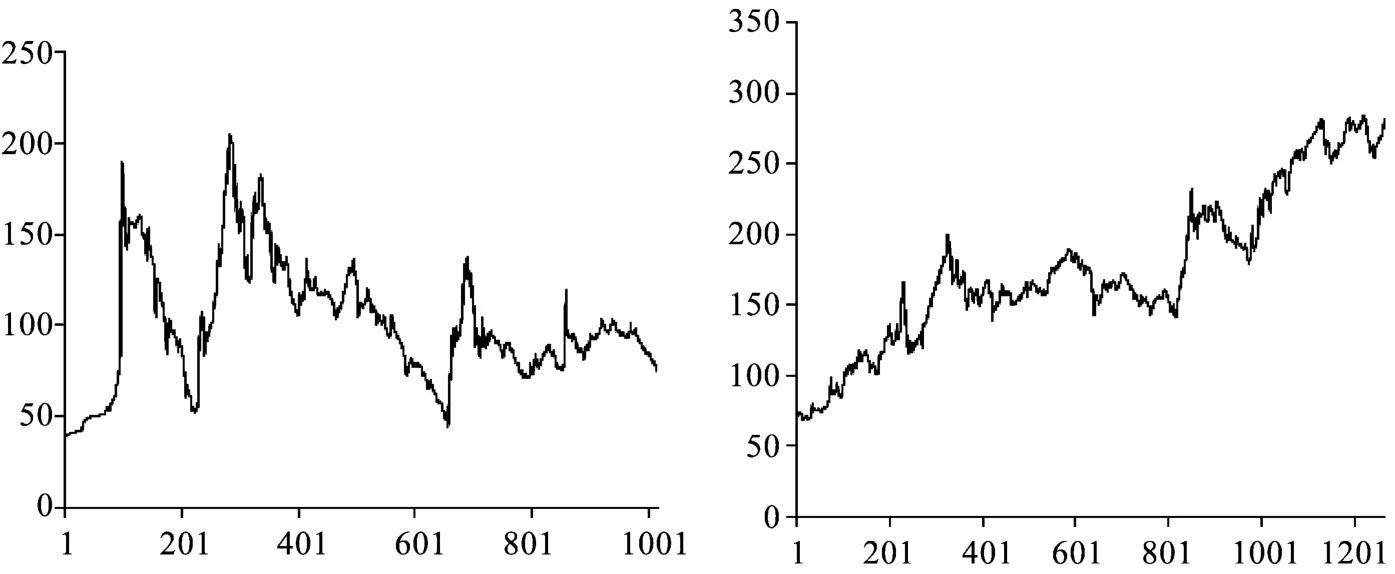
图2 SR1和SR2样本区间A股指数时序图（分段样本）

图3 SR3和SR4样本区间A股指数时序图（分段样本）

如图1至图3所示，以B－P结构性断点检验方法为基础划分的样本区间中，以A股市场为代表的股权风险资产收益率具备不同的短期走势特征。其中，第一区间为1992年1月至1995年12月，这一区间的时序图正如描述统计得到的结论那样，存在较大的波动性，期间虽然存在几波幅度较大的涨势，但其后的跌幅同样显著且剧烈；SR2代表1996年1月至2001年7月，这一阶段就整体而言代表了一波市场的涨势，且波动性与第一区间相比放缓趋势明显；第三区间为2001年8月至2005年11月，这一阶段的市场走势与前一阶段相比出现了反转，A股指数掉头向下，区间中部虽有一段较为显著的向上波动趋势，但并未逆转整体市场走低的趋势；第四区间为2005年12月至2009年6月，结合图3可以发现，这一阶段的A股市场有一个较为显著的波峰，出现在期间中段，但就整体而言该区间市场呈涨势；第五区间SR5为2009年7月至2012年12月，如图4所示，这一阶段的短期市场特征与第三区间类似，在前一区间的涨势过后出现下跌。

开篇部分提到，从一般意义上来说，股票市场可作为宏观经济发展的“晴雨表”。在理性预期框架下，股票市场价格波动是宏观经济周期的先行指标。从理论角度来说，二者间存在如此关系的机理是，股票市场价格中所蕴含的未来现金流信息直接影响实体经济中的生产活动，由此对宏观经济波动有预测和警示的作用，对实体经济活动有着重要的借鉴和指导意义。而我国股票市场是否能够如理论所述，如实反映宏观实体经济活动的运行特征呢？

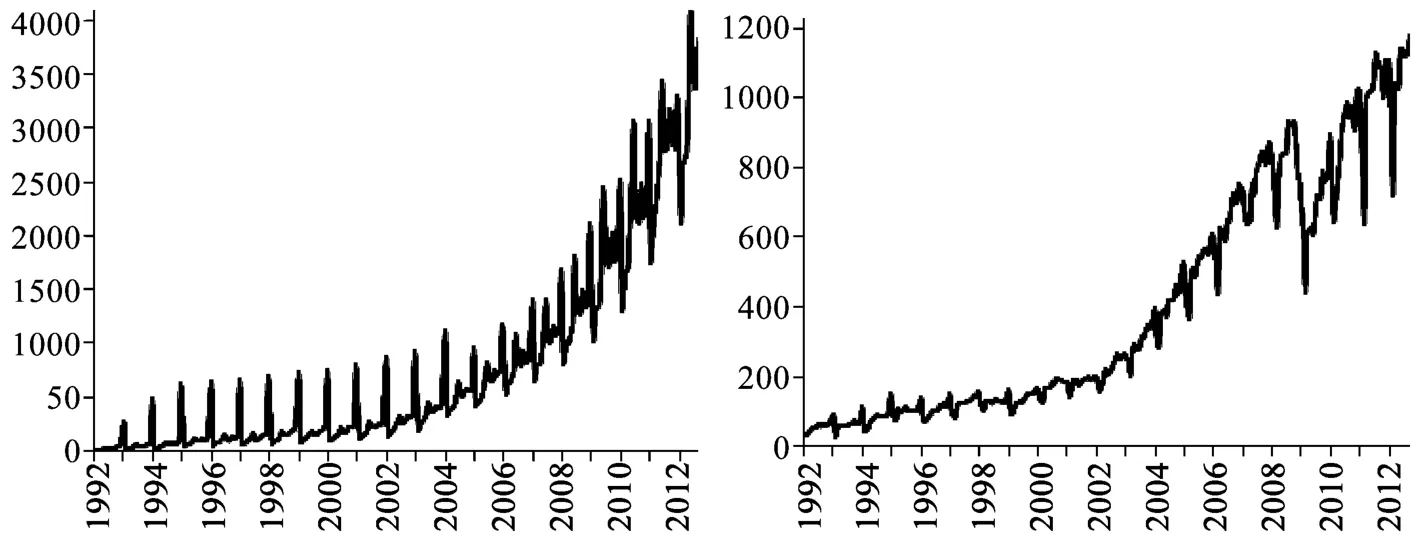
图5 我国固定资产投资与出口额月度数据时序图（全局样本）

图6 我国居民消费与国内生产总值月度数据时序图（全局样本）

笔者借助CEIC数据库得到我国1992年1月至2012年12月间的社会消费品零售总额月度数据、固定资产投资总额月度数据、国际贸易出口总额月度数据和国内生产总值月度数据①数据库中，国内生产总值实际为季度数据，月频数据以月度工业增加值与季度工业增加值的比值作为权重计算得到。，并利用如上数据生成时序图（如图5和图6所示）。通过与图2至图4的股票市场各阶段走势特征进行比较可以发现，我国宏观经济在消费、投资与出口这“三驾马车”驱动下，整体来看国内生产总值走势平稳且增势显著，并未与以A股为代表的股票市场在走势特征上体现出一致性，部分区间的整体股市行情走势甚至与宏观经济核心指标的走势特征相比出现背离。

在时序图比较的基础上，笔者进一步通过回顾相关研究发现，通过计量分析的方法探寻股票市场与宏观经济之间的关系是国内学者的研究热点。这些研究尽管采用的研究方法角度不同、研究的目标市场不同、研究的时段选取不同，但在长期趋势和波动性等统计标准的考核中，二者之间关系较为微弱或不存在相互影响关系的证据被大量发现［18－20］。由于该问题并非本文研究的核心问题，笔者无意在此对本文数据展开系统性的计量分析再行加强这些证据的说服力。结合国内学者们的发现和本文的研究结果，笔者整体上认为，一方面，我国资本市场建立时间尚短，体系仍不完备，相关的法律法规制度依然不健全，二十几年间一直处在不断完善的阶段，故与理性预期框架的假设表现出了不一致的特征；另一方面，股票市场市场运行与宏观实体经济运行缺乏关联性，股票市场价格的波动并不能正确描述实体经济的波动，其运行规律脱离于宏观经济波动规律。

五、研究结论

本文首先结合描述性统计和非线性门限自回归的方法分析了我国股权风险溢价的长期趋势和数据特征；其次，利用多重结构性断点检验的方法进一步考察了我国股权风险溢价在短期体现出的时变特征。整体而言，我国历史的股权风险溢价存在以下几点特征事实：

第一，1992年至2012年间，我国的年度溢价的算数均值达到16．53%，几何均值为4．19%，尽管溢价的整体算术均值较高，但各年度的溢价水平起伏不定，由此也造成几何均值与算数均值相比存在较大的差距。通过分析具体的数据结构发现，在多数年份，我国投资者持有高风险的A股指数带来的年度收益率不及投资于国债或银行存款等风险较低的资产所能获得的收益率，直观表现为溢价水平出现负值，代表我国证券市场中金融资产的风险与收益在部分时段出现错配。

第二，就长期而言，我国股权风险溢价的当期水平与其历史水平，尤其是最近一期的水平存在较为显著的关系，内生调整过程更多地体现出了非线性的特征，且长期来看溢价序列具备平稳性。整体来说代表我国的股权风险溢价存在与西方成熟市场较为一致的均值回归趋势。本文研究发现，我国资本市场股权溢价水平二十余年的长期趋势特征与在西方百年历史的成熟市场中得出的实践结论相近：尽管市场走势持续波动，溢价绝对水平在时间维度中不断变化，但长期而言，投资股权风险资产带来的超额回报率向均值回稳的迹象较为显著。

第三，从短期来看，我国股权风险溢价的整体时间序列中存在结构性突变因素，考虑这些因素后划定的样本区间显示，各区间市场走势各异，大幅涨跌与短期波动性并存。此外，与我国宏观经济稳步增长的发展态势相比，我国以A股市场为代表的证券市场并未表现出与之相匹配的走势特征，我国股票市场的价格形成机制不仅与经典微观金融理论缺乏一致性，且与宏观经济的运行机制缺乏必要的联动关系。

［1］杜海凤，王晓婷．股权溢价研究［J］．经济论坛，2011（8）：104－108．

［2］廖理，汪毅慧．中国股票市场风险溢价研究［J］．金融研究，2003（4）：23－31．

［3］程兵，张晓军．中国股票市场的风险溢价［J］．系统工程理论方法应用，2004（1）：14－19．

［4］冯玉梅，肖建祥．我国主板、中小板和创业板股票IPO抑价比较研究，山东财政学院学报，2014（1）：18－23．

［5］KAPETANIOSG，SHIN Y，SNELL A．Testing for a Unit Root in the Nonlinear STAR Framework［J］．Journal of Econometrics，2003，112：359－379．

［6］KILIAN L，TALYOR M P．Why is it Difficult to Beat the Random Walk Forecast of Exchange Rates［J］．Journal of International Economics，2003（60）：85-107．

［7］NARAYAN PK．Are the Australian and New Zealand Stock Prices Nonlinear with A Unit Root？［J］．Applied Economics，2005，37（18）：2161－2166．

［8］CANER M，HANSEN B．Threshold Autoregression with a Unit Root［J］．Econometrica，2001，69：1555-1596．

［9］CANER M，HANSEN B．Instrumental Variable Estimation of a Threshold Model［J］．Econometric Theory，2004，20：813－84．

［10］FAMA E F．Efficient Capital Markets：A Review of Theory and EmpiricalWork［J］．Journal of Finance，1970，25：383－417．

［11］DIMSON E，MARSH P，STAUNTON M P．Global Investment Returns Yearbook 2006［M］．London Business School，2006a．

［12］CHOW G C．Tests of Equality between Sets of Coefficients in Two Linear Regressions［J］．Econometrica，1960，28（3）：591-605．

［13］BROWN R L，DURBIN J，EVANSJM．Techniques for Testing the Constancy of Regression Relationships over Time［J］．Journal of the Royal Statistical Society，1975，37：149-163．

［14］ZEILEISA，KLEIBER C，KRAMERW，HORNIK K．Testing and Dating of Structural Changes in Practice［J］．Computational Statistics＆Data Analysis，2003，44：109－123．

［15］BAI J，PERRON P．Estimating and Testing Linear Models with Multiple Structural Changes［J］．Econometrica，1998，66：47－78．

［16］BAIJ，PERRON P．Computation and Analysis ofMultiple Structural Change Models［J］．Journal of Applied Econometrics，2003，18：1－22．

［17］程刚，张珣，汪寿阳．原油期货价格对现货价格的预测准确性分析［J］．系统工程理论与实践，2009（8）：11－18．

［18］赵蓉．试论中国股票市场失衡及其与宏观经济运行态势的背离［J］．南开管理评论，2000（6）：48－56．

［19］朱东辰，余津津．中国股市波动与经济增长关系的实证分析［J］．经济科学，2003（2）：23－30．

［20］崔杰，覃富勇，廖佚．我国股票市场与宏观经济关系的实证分析［J］．统计与决策，2011（8）：124－127．

Trends and Features of China Equity Risk Prem ium——An Empirical Study via TAR model and B－PMSCModel

ZHENG Xiao-ya
（Asset Liability Management Department，China Construction Bank，Beijing 100033，China）

Aftermore than 20 years of rapid expansion，Chinese stock market has gained remarkable achievementswhile its development and reform have entered＂deep water area＂．How to find out the existing problems and promote themarket reform becomes the focus of attention of regulators and academics．This paper，taking Equity Risk Premium（ERP）as the starting point，is aimed at analyzing the developing process and features of China stock market in order to locate the problems and defects in its development process．The study finds thaton the whole China＇s premium arithmetic average is high with the annual premiums fluctuatingwhile inmost years the risks and benefitsmismatch with high ERP and high volatility coexisting，and that in terms of short－term and long－term trends in premium the secular trend of ERP is statistically and sequentially smooth with amean reversion tendency similar to western maturemarketswhile there existnoticeable structural breaks in ERP serieswith a trend of local premium features and macro－economy robust growth threatening to depart．

equity risk premium；threshold autoregressivemodel；B－PMultiple Structure Change Model

F830．91

A

1008－2670（2014） 06－0024－13

（责任编辑 高 琼）

2014－07－30

国家自然科学基金面上项目“我国股市投机性泡沫识别和投资者乘骑泡沫行为研究”（71071132）。

郑晓亚，男，贵州贵阳人，经济学博士，中国建设银行股份有限公司资产负债管理部，研究方向：公司金融、投资基金、商业银行经营与管理。