悬臂式涡街流量传感器频率特性优化方法

孔令稳， 邵颖健， 叶凌云

(1.浙江大学 生物医学工程与仪器学院，浙江 杭州 310027；2.宁波东驰测控技术有限公司，浙江 宁波 315400)

悬臂式涡街流量传感器频率特性优化方法

孔令稳1， 邵颖健2， 叶凌云1

(1.浙江大学 生物医学工程与仪器学院，浙江 杭州 310027；2.宁波东驰测控技术有限公司，浙江 宁波 315400)

针对悬臂式涡街流量传感器固有频率较低，在大流量测量时信号失真较大的问题，研究了其固有频率的影响因素，并提出了固有频率的提高方法。仿真结果与实际测试表明：传感器悬臂梁总长度与上下部长度比例k是影响固有频率的主要因素。通过优化传感器的两项参数，125 mm口径的传感器固有频率从原来的1 620Hz提高到2 880 Hz，提升幅度达77.7 %。

涡街流量传感器； 固有频率； 数值仿真； 悬臂梁

0 引 言

流量测量作为检测技术的重要组成部分，与压力、温度和位移测量统称为过程控制的四大参数测量[1]。在诸多类型的流量仪表中，悬臂式涡街流量传感器根据卡曼涡街原理实现流量测量。由于响应速度快、信号强度大等优势，悬臂式涡街流量传感器在轻工、化工、电力、冶金、城市公用事业等领域中都得到了广泛的应用[2,3]。然而，悬臂式涡街传感器在实际测量中存在固有频率较低的缺点，当进行较大流量的测量时，由于信号频率向固有频率接近，固有频率点上的干扰将迅速增加，从而影响仪表在大流量测量时的精度。

为了克服悬臂式涡街传感器固有频率较低的缺点，目前最为常见的手段主要通过传感器信号调理电路的方法对噪声信号进行分离。2005年，杜清府[4]对悬臂式涡街流量传感器的固有频率进行了分析研究，利用2个二阶滤波器串联设计了四阶低通滤波器，对固有频率信号取得了较好的滤除效果。2006年，闫战科等人[5]通过频谱分析指出，涡街干扰信号既有高频段干扰又有低频段的干扰，高频段干扰占干扰的大多数，而且大多分布在真实流量频率信号的附近，针对该问题设计了基于椭圆滤波器的高衰减比滤波器，通过仿真和实验，滤波效果较明显。

然而，当信号频率与固有频率接近时，利用滤波器分离固有频率干扰的效果将非常小。为了克服这个问题，本文针对悬臂式涡街流量传感器的机械结构，利用理论分析和数值仿真的方法，研究传感器固有频率的影响因素。通过合理设计传感器的各项影响因素，达到提高传感器固有频率的目的。最后，通过仿真和实际测试进行理论验证。

1 传感器固有频率的影响因素分析

悬臂式传感器的结构如图1所示，通过传感器中部的圆盘与流量计壳体固定，下部的悬臂梁置于流量测量管道内，通过检测管道内的涡街信号获得相应的流量信息。

图1 悬臂式传感器结构示意图Fig 1 Structure diagram of cantilever sensor

在悬臂梁内部，两片压电片对称放置在不锈钢中性轴两侧，整体结构通过胶水灌封在悬臂梁腔体内。两压电片外侧相连组成一个电极，中性轴组成另一个电极，分别引出端线作为传感器的正负两极输出。当管道流体因为漩涡发生体产生涡街后，伴随产生的交变升力作用在悬臂梁下部的扁平体，使两侧的压电片受到不同方向的应力，从而产生出与交变升力对应的电荷，通过后续的一系列信号处理电路，最终获得流量信息。

然而这种由涡街产生的交变升力也会激发传感器的固有频率振动，这种干扰振动同样会产生相应的电荷信号，导致压电片输出信号包含固有频率的干扰成分，如图2。随着流量的增大，信号频率也会逐渐增大。当信号频率接近固有频率时，被激发的固有频率振动将会迅速增大，使传感器的输出信号质量大大降低。

图2 含有固有频率干扰的传感器信号Fig 2 Sensor signal with interference of natural frequency

1.1 悬臂式传感器的理想模型分析

悬臂式传感器安装在管道后，固定端以下部分为一个变截面且内含空腔的悬臂梁，初步分析时，先将其理想化为一个圆柱形等截面悬臂梁。

对于等截面悬臂梁，由欧拉—伯努利方程[6]

(1)

悬臂梁一端固定，一端自由的边界条件

(2)

可得

(3)

这一方程关于C1,C2具有非零解的充分必要条件为

针对同一行为，用两种罪名分别规定并不为过，就如同样调整诈骗行为的诈骗罪和保险诈骗罪即各有存在必要，这是为了刑法在社会生活中编织出更加严密的法网，充分实现罪刑法定原则的公平正义理念。

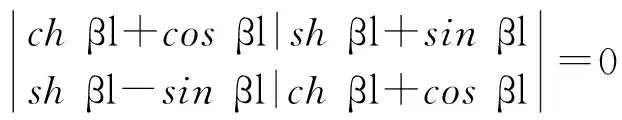
(4)

经简化后可得

cosβlchβl=-1.

(5)

此即悬臂梁弯曲振动的特征方程，由此可得等截面悬臂梁的一阶固有频率为

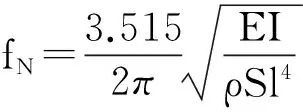
(6)

其中，fN为固有频率，E为材料的弹性模量，I为截面对中性轴的惯性矩，ρ为单位体积的质量，S为截面积，l为梁的长度。

1.2 悬臂式传感器的真实模型

在实际使用的悬臂式涡街流量传感器中，为了保证必要的涡街受力面积，减小传感器质量和使传感器重心尽量向固定端移动，传感器悬臂梁下部一般做成舌状扁平体[7]。同时，传感器内部有一圆柱形的空腔，内埋设压电检测元件。因此，在实际计算传感器固有频率时，不能将其视为连续体。

如图1所示，在分析非理想传感器模型时，可以将这个非理想模型分为L1，L2两部分。上部L1部分是可视为带空腔的等截面梁，空腔内充满封装材料，下部L2部分近似为片状结构。L1部分由于内含空腔，所以,梁的长度、截面面积、材料属性、空腔的大小、灌封材料的属性等因素都会影响到传感器的固有频率。而对于L2部分，影响传感器固有频率的因素主要有片状结构的长度、厚度和宽度。由于传感器外壳材料和空腔封装材料已基本固定，密度和弹性模量没有很大改变空间。因此，只需考虑通过优化悬臂梁的结构尺寸来提高传感器的固有频率。由于梁结构的不规则性，要得到该模型下固有频率的解析式将非常复杂。对于这个非理想模型，本文将通过数值仿真的方法，得到各结构尺寸单独变化的情况下，传感器固有频率的变化规律了。

2 实验结果

2.1 基于Ansys的固有频率仿真结果

利用Ansys的模态分析方法[8,9]，导入实际的传感器结构模型，并进行详细的结构体材料参数设定后，在其他影响因素固定不变的情况下，观察传感器固有频率随着某一个影响因素的变化规律，为优化传感器结构提供参考。

如图3，使L1与L2的长度比例固定为1︰1，观察梁的总长度L与固有频率的变化规律。可见，在非理想模型下，传感器固有频率随着梁总长的增加而减小。在总长L从16mm增加至88mm的过程中，传感器固有频率从28kHz降低到780Hz。其结果符合1.1节中理想模型所得公式的变化规律。

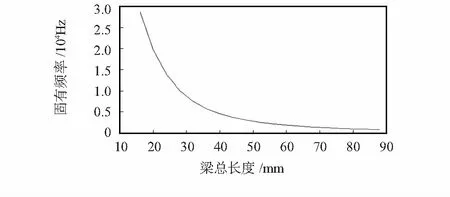
图3 固有频率关于梁总长度L的变化规律Fig 3 Change rule of natural frequency vs total length of cantilever

对于非理想的传感器模型，L2部分的片状结构是造成固有频率与理想模型的推导结果产生较大差异的最大原因。为了观察L2部分片状结构的影响，在仿真实验中，使传感器的总长度L固定为63 mm，改变L1与L2的比例，观察传感器固有频率关于比例的变化规律。

如图4所示，比例系数从0.3变化到6.8的过程中，固有频率在比例系数为1.6时出现峰值，达到了2 353 Hz。

从公式(6)可知，导致图4这一变化规律的主要原因是:在比例系数较小时，传感器的等效截面转动惯量I的增加对于固有频率的增加起主导作用;当比例系数逐步增大，由于此时L1部分所占比例较大，在公式(6)中，等效截面积S的变化对于固有频率起主导作用。因此，在L1与L2的比例系数中，存在一个固有频率的极值点。

图4 固有频率关于比例系数k的变化规律Fig 4 Change rule of natural frequency vs ratio coefficent k

此外，由于涡街流量计结构的限制，传感器中悬臂梁的截面积S的变化范围较小。对截面积S进行与上述相同的仿真实验，在截面积S允许的变化范围内，固有频率的变化较小。因此，在传感器非理想模型下，影响传感器固有频率的主要因素是悬臂梁的总长度L与L1,L2的比例系数。

2.2 实测结果

根据2.1节的结果，对一个用于125mm口径的悬臂式涡街流量传感器进行优化，提高其固有频率。优化前与优化后的参数如表1。

表1 涡街流量传感器各项参数优化前后对比Tab 1 Comparison of parameters of sensors of vortexflow sensor before and after optimization

从表1可见，通过改变总长度L与L1,L2的比例系数，传感器固有频率获得了明显的提高，提高比例达77.7 %。此外，比较仿真结果与实测结果，由于仿真实验中对于材料属性的设定、实测实验中测量误差等因素，2组结果存在10 %左右的误差，属于正常现象。

3 结 论

针对悬臂式涡街流量传感器固有频率较低，在测量大流量信号时误差较大的缺点，研究了传感器固有频率的影响因素。与其他解决固有频率问题的研究相比，本研究针对传感器悬臂梁结构的物理性质进行了优化，利用直接提高传感器固有频率替代滤波器的方法，实现传感器输出信号的优化。通过仿真实验和实测结果可以看出:传感器的悬臂梁总长度L与其上下部分的长度比例系数k是影响固有频率的主要因素。根据这一结论，用于125 mm口径的传感器固有频率从原来的1 620 Hz提高到2 880 Hz，提高幅度达77.7 %。

[1] 邢 娟.涡街流量计工况条件适应性研究[D].天津：天津大学,2009.

[2] Venugopal A,Agrawal A,Prabhu S V.Review on vortex flowmeter-Designer perspective[J].Sensors and Actuators A：Physical,2011,170(1-2):8-23.

[3] Miau J J,Hu C C,Chou J H.Response of a vortex flowmeter to impulsive vibrations[J].Flow Measurement and Instrumentation,2000,11(1):41-49.

[4] 杜清府.压电晶体式涡街流量传感器放大电路的设计[J].自动化仪表,2005,26(3):52-54.

[5] 张宏建，孙志强，闫战科，等.涡街频率检测电路的改进研究[J].仪表技术与传感器,2006(4):35-38.

[6] 高淑英,沈火明.线性振动教程[M].北京：中国铁道出版社,2003.

[7] 赵 超.基于TMS320F2812的抗振型数字涡街流量计的研制[D].天津：天津大学,2009.

[8] 曹延欣.有限元分析软件ANSYS及其使用[J].大众科技，2008(2):55-56.

[9] 杨笑冬.基于ANSYS的悬臂梁模态分析[J].机电一体化，2008(6):58-60.

Optimization method of frequency characteristics of cantilever vortex flow sensor

KONG Ling-wen1， SHAO Ying-jian2， YE Ling-yun1

(1.College of Biomedical Engineering & Instrument Science, Zhejiang University,Hangzhou,310027,China；2.Ningbo Dongchi Measuring Technology,Co Ltd,Ningbo 315400,China)

Aiming at problem that cantilever vortex flow sensor has low natural frequency,signal distortion is large in large flow measurement，factors that affect natural frequency are studied,and the method to improve natural frequency is proposed.Simulation results and experimental test show that the ratio of the length of cantilever respective length of the upper and lower part is the main factor which affects natural frequency.By optimizing these two factors,natural frequency of the sensor with 125 mm caliber is increased from 1 620 Hz to 2 880 Hz,enhancing rate is 77.7 %.

vortex flow sensor; natural frequency; numerical simulation; cantilever

10.13873/J.1000—9787(2014)08—0059—03

2014—02—12

TP 274

A

1000—9787(2014)08—0059—03

孔令稳(1988-)，女，山东菏泽人，硕士研究生，主要从事流量测量、传感器信号分析研究。