双直立锁边板的辊弯成形数值模拟与工艺研究

祁宏伟，韩 飞

（北方工业大学 机电工程学院，北京100144）

冷弯型钢具有断面均匀、力学性能良好、产品质量高、能量消耗低等优点, 因此在建筑、汽车、交通、航空等各个行业得到广泛应用。辊弯成形是冷弯型钢主要的成形方法，但是其成形过程十分复杂,主要变形过程包括横向弯曲、纵向拉伸以及横向剪切等，具有非常明显的材料非线性、几何非线性和接触边界非线性等，并且影响辊弯成形的因素非常多，要对其成形过程进行精确模拟很困难。在实际生产中,辊型的设计和产品的加工主要依靠经验来进行, 这样很容易造成孔型设计和产品质量的不确定性, 从而影响最终成形过程[1-2]。

目前国内外学者对辊弯成形的研究越来越多，而利用有限元分析能够更快捷高效地对辊弯成形过程进行模拟，获得板料成形过程的规律。M.Brunet 等[3]对U 型截面的辊弯成形过程进行数值模拟，成功预测出成形后的应力应变分布情况。Q.V.Bui 和J.P.Ponthot[4]利用有限元仿真得到了成形过程中的纵向应变，并通过实验进行了验证。曾国等[5]利用有限元软件ABAQUS 研究了工艺参数对槽形截面回弹的影响，并通过响应面法得到了最优弯角增量和下辊半径。罗晓亮等[6]基于有限元模拟的方法研究了材料参数和工艺参数对高强钢辊弯回弹的影响。李冰等[7]通过对压型板辊弯成形的全过程进行模拟分析，得到了板料变形过程中的一些规律，证实通过有限元模拟探索辊弯成形规律的可行性。

本文利用有限元软件ABAQUS，基于动力显式算法建立双直立锁边板多道次辊弯成形有限元模型, 对锁边板的辊弯成形过程进行数值模拟, 通过对模拟结果的分析, 获得板料在多道次成形辊作用下的变形规律, 为优化锁边板多道次辊弯成形工艺提供理论依据，并且通过正交试验进一步分析研究了工艺参数对锁边板回弹的影响。

1 有限元模型建立

1.1 材料试验

本次仿真中选择的材料为SUS304 不锈钢，厚度为0.5mm，材料化学成分如表1 所示。由表中可知SUS304 的Ni 含量相对较高，这也是其具有较高的韧性以及较好的冷作成形和焊接性的主要原因，同时Cr 的含量达到17.00%～19.00%，这让其具有良好的防锈性和耐腐蚀性。

表1 SUS304 不锈钢化学成分（%）

通过静态非接触式测量系统进行单拉试验，获得的数据导入到Origin8.0 中进行数据处理，取平均值，最后获得了试样的真应力-真应变（σ-ε）曲线如图1所示，从图中可看出，材料具有明显的应力强化阶段，延伸率δ 达到0.43，显示出较强的塑性变形能力，进一步处理后得到SUS304 的材料参数如表2 所示。

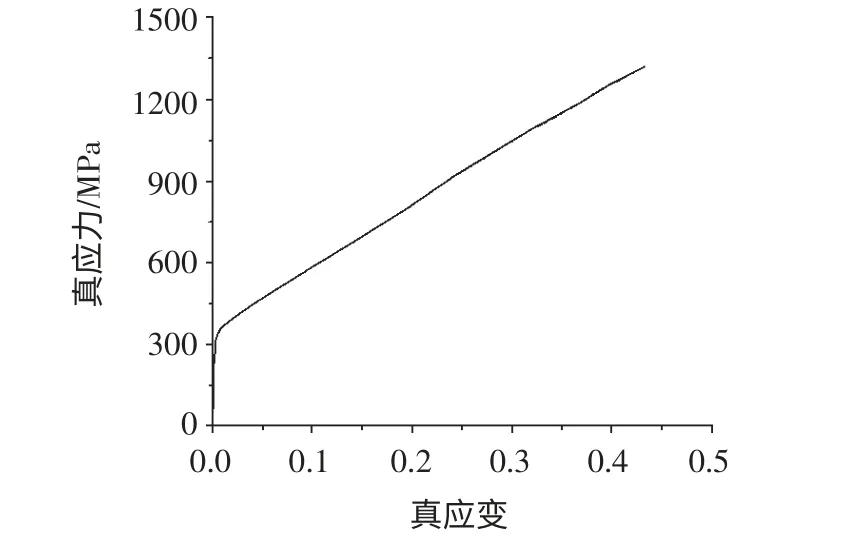
图1 SUS304 不锈钢拉伸试验真应力-真应变曲线

表2 SUS304 不锈钢的材料参数

1.2 有限元建模

锁边板在国外应用的很多，主要应用在屋面板和房顶上，通过将双直立锁边板的一边扣到另一块板上，然后利用锁边机将两块板连接上，其截形如图2 所示，腹板宽可以根据实际需要调整，这里整个板宽取350mm。辊型设计中，左边先对外侧第二个弯角和内弯角进行连续弯曲，当外侧第二个弯角弯曲成88°后再对左边最外侧弯角进行连续弯曲，随后是内弯角完成弯曲，最后是左边最外侧弯角完成弯曲，右边先将外弯角连续弯曲成90°，再对内弯角逐次弯曲成90°，从而得到最终的截形，辊花图如图3所示，生产中板料线速度为20m/min，板料厚度0.5mm。

图2 双直立锁边板截面尺寸

图3 双直立锁边板辊花图

本文利用ABAQUS 进行有限元仿真，采用动力显式算法，由于轧辊形状规则, 为减少计算成本, 提高接触计算与板料成形精度, 轧辊采用解析刚体。考虑到多道次辊弯成形具有较强的非线性, 使用四边形壳单元S4R，为减少计算规模，同时保证计算精度，对板料弯角处网格做细化处理,整个过程采用板料不动，轧辊向板料运动的加载方式，最终建立的有限元模型如图4 所示。

图4 有限元模型

2 计算结果与分析

2.1 等效应力分析

如图5 为板料成形后的形状及应力云图，从图中可以看出成形质量较好,没有袋形波、边部褶皱等不良质量问题。应力主要集中在型材两边的成形区域，中间腹板处应力很小，几乎为0，其中型材前端应力较其他地方应力更大一些，这可能是由于成形过程中板料在进入轧辊前，前端与轧辊发生冲击产生的结果。为了对成形的结果进行更深入的分析，提取锁边板截面上一排连续的点A、B、C、D、E、F、G，如图6 所示。

图5 等效应力云图

图6 提取截面上一排连续的点

2.2 边部纵向应变分析

图7 显示了在整个成形过程中，型材左、右两边翼缘边部的点A、G 的纵向应变变化情况。由图中可知，A 点的纵向应变在成形过程中的规律非常明显，在前8 道次成形辊处，双直立锁边板左边翼缘边部的纵向应变交替变化，在进入成形辊时受到拉应变，而在出成形辊时受到压应变。在第9 道次时虽然也基本遵循这个规律，但是拉压应变变化不明显，这可能是由于这一道次较前面几道次，成形区变形量不是很大，第10 道次时纵向应变基本没有变化，这可能是由于第十道次相对于第九道次成形区变形量更小。G 点的纵向应变在前三个道次时变化剧烈，也是在进入成形辊时受到拉应变，出成形辊时受到压应变，从第4 道次开始由于型材右边边缘处与上辊不再接触，因此G 点处的纵向应变变化不大。

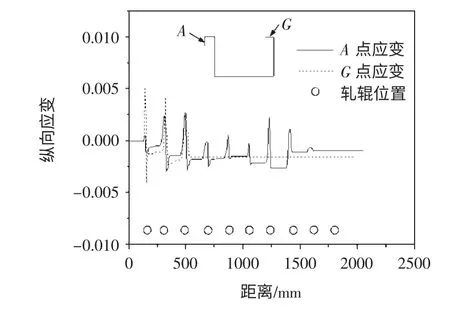
图7 边部纵向应变

2.3 弯角处厚度分析

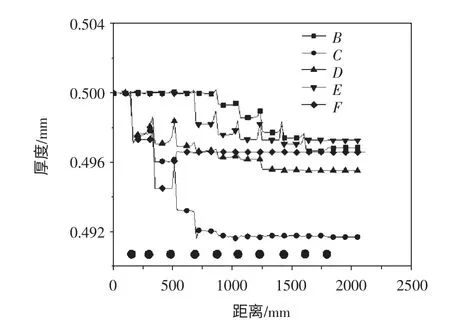
图8 弯角处厚度变化

图8 是弯角处B 点、C 点、D 点、E 点、F 点在成形过程中厚度的变化曲线。第1 到第4 道次B 处弯角没有成形，因此厚度变化也不大，从第5 到第9 道次对B 点处弯角进行连续的弯曲，B 点处厚度也随之呈阶梯式逐渐减薄，第10 道次时弯角增量较小，因此厚度变化不大，最终厚度达到0.49685mm。从第1 到第5 道次，轧辊将C 处的弯角连续弯成90°，C处的厚度也随之逐渐减薄，且幅度较大，从第6 道次开始，C 处弯角不再变化，厚度变化也不大，最终厚度达到0.49168mm。从第1 到第7 道次，对D 处弯角连续弯曲成88°，D 处的厚度在这一成形过程中也逐渐减薄，从第8 道次往后，D 处弯角不再变化，因此厚度变化也不大，最终厚度为0.49549。从第1 到第3 道次，E 处弯角没有进行成形，因此这一过程中E 处厚度没有明显的变化，从第4 道次开始到第9道次将E 处弯角连续弯曲成90°，而在成形过程中E 处弯角厚度从第4 到第8 道次连续减薄，从第8到第9 道次厚度有一个小幅增加的过程，这是由于第8 道次是过弯，第9 道次重新弯回90°，最终E 处厚度达到0.49727mm。从第1 到第3 道次，将F 点连续弯曲成90°，在这一过程中板料的厚度先大幅下降，而后又大幅上升，最终厚度为0.49657mm，第3道次处厚度上升可能是由于成形方式变化造成的，在这一道次上下辊从侧面压住边腿成形。

通过以上分析可以看出，E 处弯角厚度的减薄量最小，而C 处弯角厚度的减薄量最大，纵观各个弯角处厚度变化曲线可以看出，厚度的减薄量大小不仅与弯曲的曲率有很大联系，而且同时与弯角的位置以及各部分成形的先后顺序密切相关。同时每道次减薄量的大小与弯角增量有很大关系，弯角增量越大，每道次减薄量越大，在图上显示的结果是阶梯下降幅度越大。

2.4 沿宽度方向横向应变分析及与理论值对比

图9 为双直立锁边板横截面处上下表面横向塑性应变沿宽度方向分布情况。图9 表明,从整体上来看，在弯角处横向应变较大，并且出现了峰值，而在腹板处板料横向应变几乎为0，且没有什么变化。从上表面来看，左边的两个外弯角受到拉应变,内弯角受到压应变，右侧的两个弯角都受到压应变，而板料下表面的情况正好相反，这与实际情况是相符的。内弯曲半径为2mm 的弯角处最大拉应变为0.121，最大压应变为0.09，内弯角半径为3mm 处最大拉应变为0.085, 最大压应变为0.068。

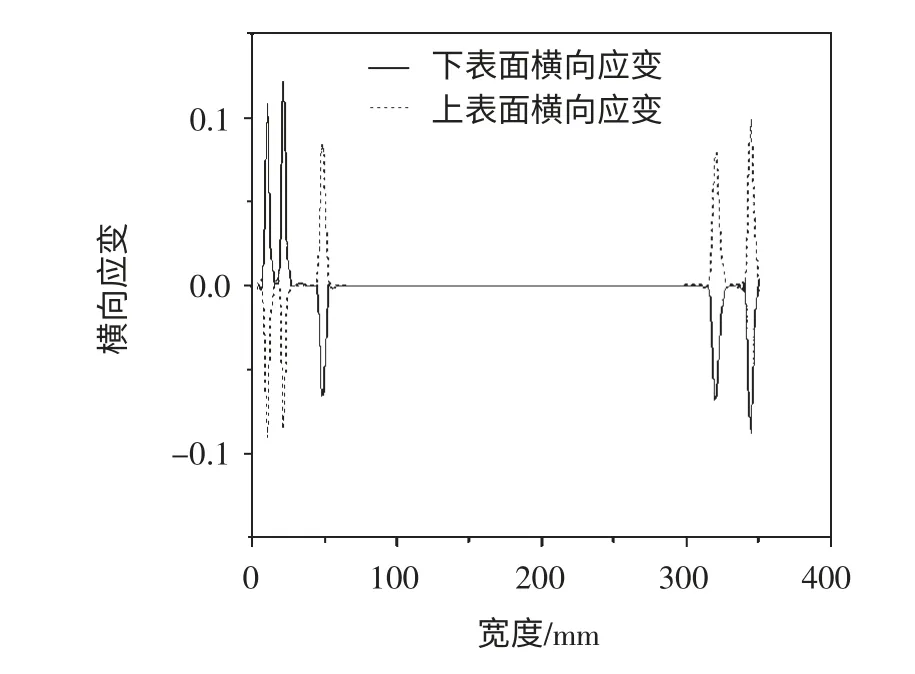
图9 横向应变沿宽度方向分布

根据经典的平板宽板弯曲理论[8]可得，内外表面最大切向应变为：

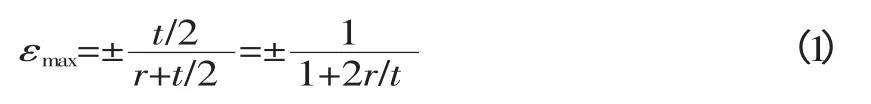
式中：r——内圆角半径；

t——板料厚度。

根据上式，此时弯角处的最大切向应变为：

对比数值模拟和理论计算的最大切向应变值，可以看出结果基本相符, 证明了数值模拟的有效性。但是从结果上来看仍有一些差别，这是由于公式（1）的前提是假设板料不变薄且中性层仍在板料中间, 但是实际上辊弯成形过程中，板料发生三维大变形,成形过程复杂，存在厚度减薄和中性层向内移动的情况, 所以才导致最大切向应变偏差的产生。

3 工艺参数对锁边板回弹的影响

3.1 正交试验方案设计

为了更好地获取锁边板的成形规律，文中主要选取板厚、道次间距、下辊半径、成形速度为影响因素，而每一个因素又选择3 个水平，并且忽略设计变量之间的交互影响，按照试验标准设计正交试验。参数的选取都按照真实的工况来进行，板厚以0.4mm开始，以0.1mm 递增，最大为0.6mm，道次间距最小为200mm，以50mm 递增，最大为300mm，下辊半径以40mm 开始，每5mm 递增，最大为50mm，成形速度以20m/min 开始，每10m/min 递增，最大为40m/min，根据以上正交试验的设计，建立的因素水平表如表3 所示。

3.2 正交试验结果与分析

所有试验完成以后，对数据进行处理，这里主要以弯角D 处回弹角为评价指标，所以每组试验中分别取板料三处的弯曲度数，然后对比初始设计的度数，得到回弹角，最后对其取平均值，L9（34）组正交试验表及试验结果如下表4 所示。

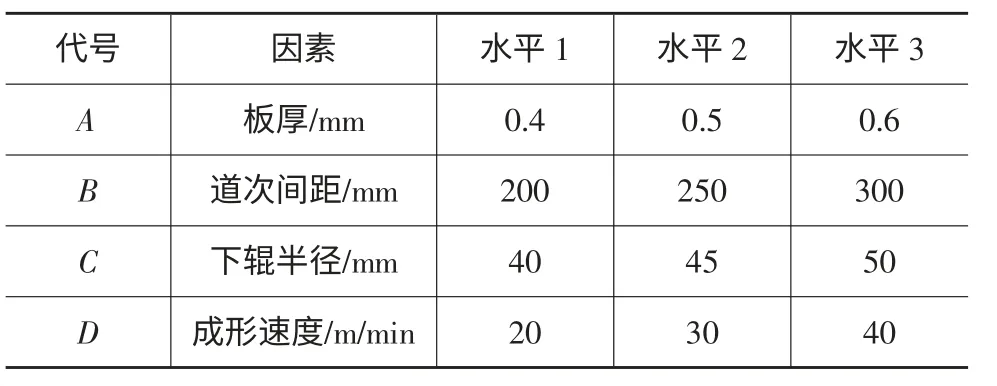
表3 正交试验因素水平表

表4 锁边板正交试验表

各因素在不同水平下与回弹角度的关系如下图10 所示,从图中可以看出,板料厚度对回弹的影响的曲线波动大并且具有单调性，这充分说明其对回弹的敏感性较大并且不容易受到其他因素的干扰。其他三个因素相对于板厚对回弹的敏感性要小一些，道次间距的曲线有一个先上升而后缓慢下降的趋势，随着下辊半径逐渐增大，回弹角有逐渐减小的趋势，而成形速度逐渐增大，回弹角先增大而后减小。

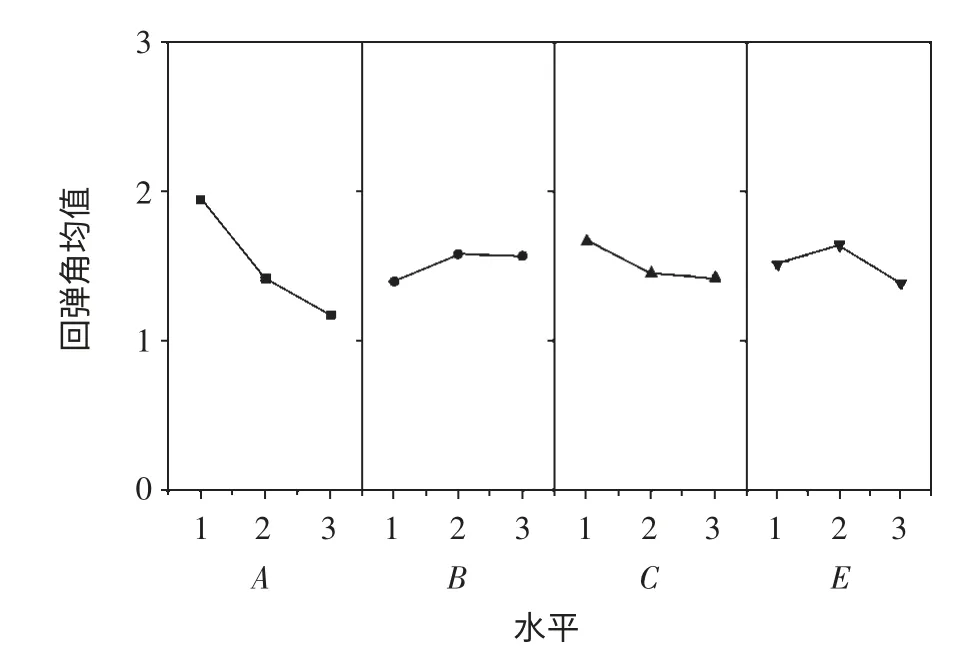
图10 因素水平趋势对比图

在这三个因素当中，板料厚度对回弹最敏感,这是由于在弯曲角度和内弯角半径相同的情况下，板料越厚，弯角部分产生塑性变形的区域越大，卸载以后回弹也就越小。

4 结论

（1）通过有限元软件ABAQUS 建立了双直立锁边板的辊弯成形有限元模型，并对其进行数值模拟，结果显示双直立锁边板在成形过程中，两边边部的纵向应变变化剧烈，并且在进入成形辊时受到拉应变，而在出成形辊时受到较大压应变。

（2）在辊弯成形过程中，弯角处厚度的减薄与弯曲曲率、弯角位置以及成形的先后顺序有关，同时每道次减薄量的大小与弯角增量有很大关系，弯角增量越大，每道次减薄量越大。

（3）在成形过程中，从左往右，在上表面双直立锁边板立边上的两个弯角受到横向拉应变，另外三个弯角受到拉应变，下表面情况正好相反，腹板处横向应变几乎为0，同时最大横向应变的仿真值和理论值基本相符，可以证明仿真的有效性。

（5）通过正交试验得出，板料厚度对锁边板的回弹影响最大，且不易受到其他因素的干扰，成形速度和下轧辊半径敏感性仅次于板料厚度，道次间距对回弹的敏感性最小。

[1]韩 飞，刘继英，艾正青，等.辊弯成型技术理论及应用研究现状[J].塑性工程学报，2010，17（5）：53-60.

[2]周宏宇.槽钢辊弯成型的数值模拟及工艺参数研究[D].河北：燕山大学机械工程学院，2004：1-84.

[3]M Brunet,S Mguil and P Pol.Modelling of a roll forming process with a combined 2D and 3D FEM code[J].Journal of Materials Processing Technology,1998.80-81:213-219.

[4]G.Zeng,S.H.Li,Z.Q.Yu,et al.Optimization design of roll profiles for cold roll forming based on response surface method[J].Materials and Design,2009,30（6）:1930-1938.

[5]Q.V.Bui,J.P.Ponthot.Numerical simulation of cold roll-forming processes[J].Journal of materials processing technology,2008,202（1-3）:275-282.

[6]罗晓亮，于忠奇，李淑慧，等.高强钢辊弯回弹的有限元分析[J].塑性工程学报，2008，15（5）：83-86.

[7]李 冰，张士宏，胡 林，等.压型板辊弯成型过程数值模拟[J].钢铁，2004，（8）：82-85.

[8]Dwivedi J P,et al.Springback analysis of thin rectangular bars of non-linear work-hardening materials under torsional loading[J].International Journal of Mechanical Sciences,2002.44（7）:1505-1519.

[9]张利鹏.槽钢辊弯成形过程的有限元仿真[J].锻压装备与制造技术，2005，（1）：76-78.

[10]徐元宪，魏意敬，刘长勇.辊弯成形生产线中料头料尾焊接技术的探讨[J].锻压装备与制造技术，2006，（5）：62-63.