基于迭代计算的加速度计标定方法*

戴邵武 万 龙 徐胜红

(海军航空工程学院控制工程系 烟台 264001)

基于迭代计算的加速度计标定方法*

戴邵武 万 龙 徐胜红

(海军航空工程学院控制工程系 烟台 264001)

在建立三轴加速度计数学模型的基础上,提出了一种新的三轴加速度计的标定算法。加速度计在静止状态下,各敏感轴分量的模值等于当地重力加速度的数值。通过六个不同静态位置加速度计的输出建立标定方程。采用迭代算法对加速度计的标度因子和零偏进行解算。仿真结果表明,算法能够有效标定出加速度计误差参数,并且对较大偏差的初值同样适用,且迭代过程收敛迅速,计算量小,非线性适应性较强,能够拓展标定算法的应用范围。

加速度计; 标定; 迭代法; 参数估计

Class Number TJ765.4

1 引言

捷联惯组标定是进行惯性导航的前提,标定的好坏直接影响惯性导航的精度。加速度计标定可分为分立标定和系统级标定。分立标定直接以加速度计输出为观测量,用最小二乘法标定其系数。系统级标定则是利用导航误差作为观测量,用滤波估计加速度计误差系数[4]。标定后的各项参数会随着温度、时间的改变而变化。为提高加速度计的测量精度,必须定期对其各项误差系数标定。传统加速度计的标定采用静态多位置方法,使加速度计旋转至已知的特定角度,根据不同角度下加速度计的输出解算出各项误差[2～3]。为了精确地解算出误差系数,旋转至每个位置相对于转台的角度必须精确测量,一般依靠转台或其他高精度的外部设备得到角度的量测值。标定环境要求较高,在外场环境中难以实现。本文提出一种新的加速度标定计算方法,计算过程简洁精度高。标定过程中应用重力加速度在各坐标轴分量的模值相等的条件结合建立的标定误差模型建立等式,结合加速度计在六个不同位置的输出值采用逐步迭代的方法估计标定误差系数真值。方法的优点在于每个静态位置不需要角位置的精确数值即可完成标定计算。仿真结果表明在迭代赋的初值与真实值偏差很大的情况下,标定误差系数也可以很好的收敛于真值,并且迭代次数少,绝大多数情况下迭代三步即可得到满足精度要求的标定值。

2 加速度组件的标定误差模型建立与解算过程

计载体坐标系为b系,转台坐标系为p系。在加速度组件静止条件下,加速度计各轴分量(b系,用AX,AY,AZ表示)与当地重力加速度的关系为

(1)

加速度计测量误差模型可表示为

Saxis=GaxisAaxis+Baxis

(2)

其中Saxis为加速度组件的输出,Gaxis为标度因子,是一个3×3的对角阵Aaxis为各轴敏感的加速度分量,Baxis加速度计零偏。式(2)中,Gaxis可以分解为有限个对角阵相乘的形式,相应的Baxis可以表示为有限个同样结构的矩阵相加的形式。由此式(2)可以进一步表示为

(3)

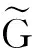
(4)

(5)

(6)

(7)

(8)

(9)

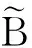
(10)

(11)

3 仿真验证

首先,确定待标定加速度组件的真实标度因数、零偏值,加速度计的数据输出值由Matalb仿真计算产生[3],实际标定实验中加速度组件六个静态位置可取任意姿态,考虑到重力环境下对加速度计的充分激励和仿真处理数据方便直观,将加速度组件各轴(X、Y、Z)分别向天向,地向一次,得到一组静态六位置加速度计输出数据。选取有代表性的五组仿真标定结果分析如表1所示。

表1 不同标度因数与零偏值的仿真标定结果

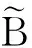
4 结语

仿真结果可以证明本文提出的迭代结算方法能准确有效估计出标度因子和零偏的值,计算过程简便易行。标定过程表明,加速度计只需六组静态位置的采样值数据,对加速度相对转台的转角,简化转台调平寻北,器件与平台对准等一系列步骤,使得标定时间缩短,为加速度计在场环境下的标定提供了新的思路。标定方法对激光陀螺是否适用有待进一步研究;加速度计安装误差系数的标定难度较大,同样是下一步研究的问题。

[1] H. J. Luinge, P. H. Veltink. Inclination measurement of humanmovement using a 3-D accelerometer with autocalibration[J]. IEEE Trans.Neural Syst. Rehabil. Eng.,2004,12(1):112-121.

[2] Z. F. Syed, P. Aggarwal, C. Goodall, et al. A new multi-position calibration method for MEMS inertial navigation systems[J]. Meas. Sci. Technol.,2007,18(7):1897-1907.

[3] 张红良,武元新,查亚兵,等.高精度惯测组合标定误差分析[J].国防科技大学学报,2010,32(1):142-146.

[4] 肖龙旭,魏诗卉,孙文胜.惯测组合快速高精度标定方法研究[J].宇航学报,2008,29(1):172-177.

[5] 谷宏强,袁亚雄,摆卫兵.捷联惯性测量组合快速位置标定[J].南京理工大学学报,2007,31(6):719-722.

[6] 严恭敏,秦永元.激光捷联惯组的双轴位置转台标定仿真[J].中国惯性技术学报,2007,15(1):123-127.

[7] 陆元九.惯性器件[M].北京:中国宇航出版社,1993.

[8] Zhu G C, Saydy L. An extended Luenberger-like observer and itsapplication to target tracking[C]//AIAA Guidance Navigationand Control Conference and Exhibit, San Francisco, August,2005:15-18.

[9] 夏家和,秦永元,赵长山.适用于低精度惯导的非线性对准方法研究[J].仪器仪表学报,2009,30(8):1618-1622.

[10] 周卫东,乔相伟,任蕾,等.QUKF算法及其在SINS初始对准中的应用[J].仪器仪表学报,2010,31(2):264-269.

[11] 孙枫,孙伟,郭真.基于IMU旋转的捷联惯导系统自动补偿方法[J].仪器仪表学报,2009,30(12):2013-2015.

[12] 刘百奇,房建成.一种改进的IMU无定向动静混合高精度标定方法仪[J].仪器仪表学报,2008,29(6):1250-1254.

Accelerometer Calibration Method Based on Iterative Calculation

DAI Shaowu WAN Long XU Shenghong

(School of Controld Engineering, Naval Aeronautical Engineering Academy, Yantai 264001)

Based on the design of triaxial acceleromeer mathmatic model, a new triaxial accelerometer callibration method is presented. When the accelerometer is safionary module value of each sensitinty axle is equal to its local grauty. Colibration equation is set through accelerometer outputs of six defferent stationary place. Iteration calculation is used to estimate gain factors and bias. The simulation result shows that the calibration method can effectively estimate error parameters of accelerometer, and can be applied in ealculating the initial value of large deviation. It has aduantages, such as small calculation work, strong nonlinear adaptability.

acceleration measurement, calibration, iterative method, parameter estimation

2013年7月1日,

2013年8月10日

戴邵武,男,硕士,教授,研究方向:导航、制导与控制。万龙,男,硕士研究生,研究方向:导航、制导与控制。徐胜红,男,博士,副教授,研究方向:飞行器导航与控制。

TJ765.4

10.3969/j.issn1672-9730.2014.01.018